基于MO-PLP-ELM及电容层析成像的两相流流型辨识
2021-04-26张立峰朱炎峰
张立峰,朱炎峰
(华北电力大学 自动化系,河北 保定 071003)
1 引 言
由于两相流系统在电力、化工、石油等工业部门广泛使用,两相流流型辨识也成为两相流在线监测的基础,是两相流测量的重要研究方向[1]。随着过程层析技术的迅速发展,出现了电容层析成像(electrical capacitance tomography,ECT)技术,该技术是基于电容敏感机理的可视化层析成像技术,由于其具有非侵入、可视化、非辐射等优势受到广泛关注[2~7]。
基于ECT的流型辨识主要分为2类:基于重建图像的流型辨识以及基于ECT测量数据,采用各种机器学习算法的流型辨识,其常见方法有:神经网络类算法[8]及统计学习类算法(如支持向量机算法)。相较而言,通过神经网络的方法进行流型辨识可以近似完成复杂的映射关系,预测结果也最为准确。常见的ECT流型辨识主要针对层流、空管、满管、核心流和环流5类流型进行辨识[1]。但在实际工业环境中,两相流流型远比这五类流型复杂,本文选取了更复杂的流型模型进行辨识,包括:单个物体、2个物体、3个物体、环状、层状、空场以及满场分布,共7类流型。使用常用的BP神经网络[9,10]、支持向量机[1,11]和极限学习机[12,13]对其进行流型辨识,发现大多方法辨识效果并不理想。Caminhas等提出了并行感知器(parallel layer perceptron,PLP)的概念,其并行分层的优势可以解决集群和云环境的精度和效率问题[14]。2004年,极限学习机(extreme learning machine,ELM)由Huang等提出,用来求解单隐层前馈神经网络(SLFNs)[13]。该算法学习速度快且泛化能力好,在一些复杂系统的控制、辨识和建模等问题上已得到了成功应用。
本文使用PLP算法改进ELM算法,由于其训练过程是一个多目标过程,为平衡经验风险和复杂性,使用多目标(multi objective,MO)优化PLP-ELM算法[15],得到MO-PLP-ELM算法[16]。最后,通过仿真实验研究了基于本算法及ECT技术的两相流流型辨识效果。
2 MO-PLP-ELM算法原理
2.1 PLP-ELM数学模型
PLP-ELM网络结构图如图1所示。

图1 PLP-ELM网络结构Fig.1 PLP-ELM network structure
PLP的输出层yi由每层的输入xi和隐层感知器h所决定[14],如式(1)所示:
(1)
其中:
aij=x′ipj
(2)
bij=x′ivj
(3)
式中:β(x),γ(x),φ(x)为激活函数(双曲正切函数、高斯函数、线性函数等);pj和vj构成权重矩阵P和V∈R(n+1)×h;i=1,2,…,n;j=1,2,…,m;xi为第i个输入,x′i为感知器偏差;yi为输出y的第i个输出向量,yi的维度仅取决于激活函数β(x)。
PLP算法和传统的前馈神经网络(SLFN)一样,在训练阶段可以调整所有的权重,但PLP和SLFN还是有一定区别的。首先,SLFN方法中,输入-输出的映射是通过函数的函数进行的,而PLP-ELM方法中则是通过应用函数的乘积来实现的。此外,PLP-ELM算法简化了并行机器或集群中的实现。
在特定情况下,当激活函数β(x)和γ(x)是线性函数时,式(1)中的神经网络yi可表示为:
(4)
将式(2)和式(3)代入式(4)中
(5)
在式(4)中所描述的特定的情况下具有一些理想特性。相对于pji的误差(线性参数)是二次结构,因此可较容易地使用最小二乘估计解。
2.2 PLP-ELM训练方法
PLP-ELM训练方法是基于最小二乘估计(LSE)调整方程(5)的线性项的训练方法。其可行性是由于样本输出yi与参数P呈线性关系是可能的。非线性参数随机初始化,无需在训练过程中对其进行调整[15]。
矩阵P到列向量的变换l可表示为:
l=[p11,…,p1(n+1),p21,…,p2(n+1),…,ph(n+1)]′
(6)
矩阵C由输入矩阵xi和非线性神经元φ(bji)组合而成,矩阵C的求解方法为:

(7)
因此,网络模型可记为矩阵模式:
y=Cl
(8)
然后,求解目标参数l的最佳值,以便最小化期望输出t和输出y之间的差异,即:
(9)
应用最小二乘法求解可得:
l*=(C′C)-1C′t
(10)
l*=C+t
(11)
式中:l*为最佳值;C+为C的伪逆矩阵。
求解l*后,将其值返回矩阵P,然后根据式(5)求得输出值。
2.3 MO-PLP-ELM算法

(12)
矩阵C的条件数与线性权重层l的范数之间存在强相关性,式(11)的解析解为:
(13)
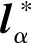
使用T-SVD分解求矩阵C的伪逆:
(14)


(15)
其中:σi为矩阵C的第i个特征值;r为特征值个数。
此时,可以规范复杂性(标准和调节次数)与经验风险(RMSE)之间的关系,从而提出MO-PLP-ELM方法。
这里提出的方法中,可以使用矩阵元素本身Σ=diag(σ1,…,σr)来规范PLP-ELM。
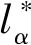
1.输入:C和T
2.[U,Σ,V]=SVD(C)
3.A=U′T
4.α=0,σr,σr-1,…,σ2,σ1
6.结束。
3 基于MO-PLP-ELM及ECT的两相流流型辨识
3.1 ECT系统原理
ECT系统分为3部分组成:电容传感器单元,数据采集单元以及图像重建单元,如图2所示。

图2 ECT系统结构图Fig.2 Structure diagram of ECT system
当管内介质分布改变时,场内混流介电常数也随之发生变化,使其电容值发生改变[1]。ECT系统就是通过不同的电容值对管内介质介电常数进行重建。本文针对12电极ECT系统进行仿真,其独立测量电容值数为66。
3.2 基于MO-PLP-ELM及ECT的流型辨识原理
在进行MO-PLP-ELM流型辨识时,首先需将样本电容数据归一化处理,表示为:
(16)
式中:λ为归一化后电容值,Cm为样本分布时的仿真测量电容值;Ce及Cf分别为空场及满场仿真测量电容值。
然后将归一化电容数据作为MO-PLP-ELM网络的输入,流型类型作为网络输出,进行训练。训练结束后,将测试样本的归一化电容值输入MO-PLP-ELM网络中,得到样本的预测流型类型,最后比较样本预测流型类型和实际流型类型的差异,验证算法精度,其过程如图3所示。
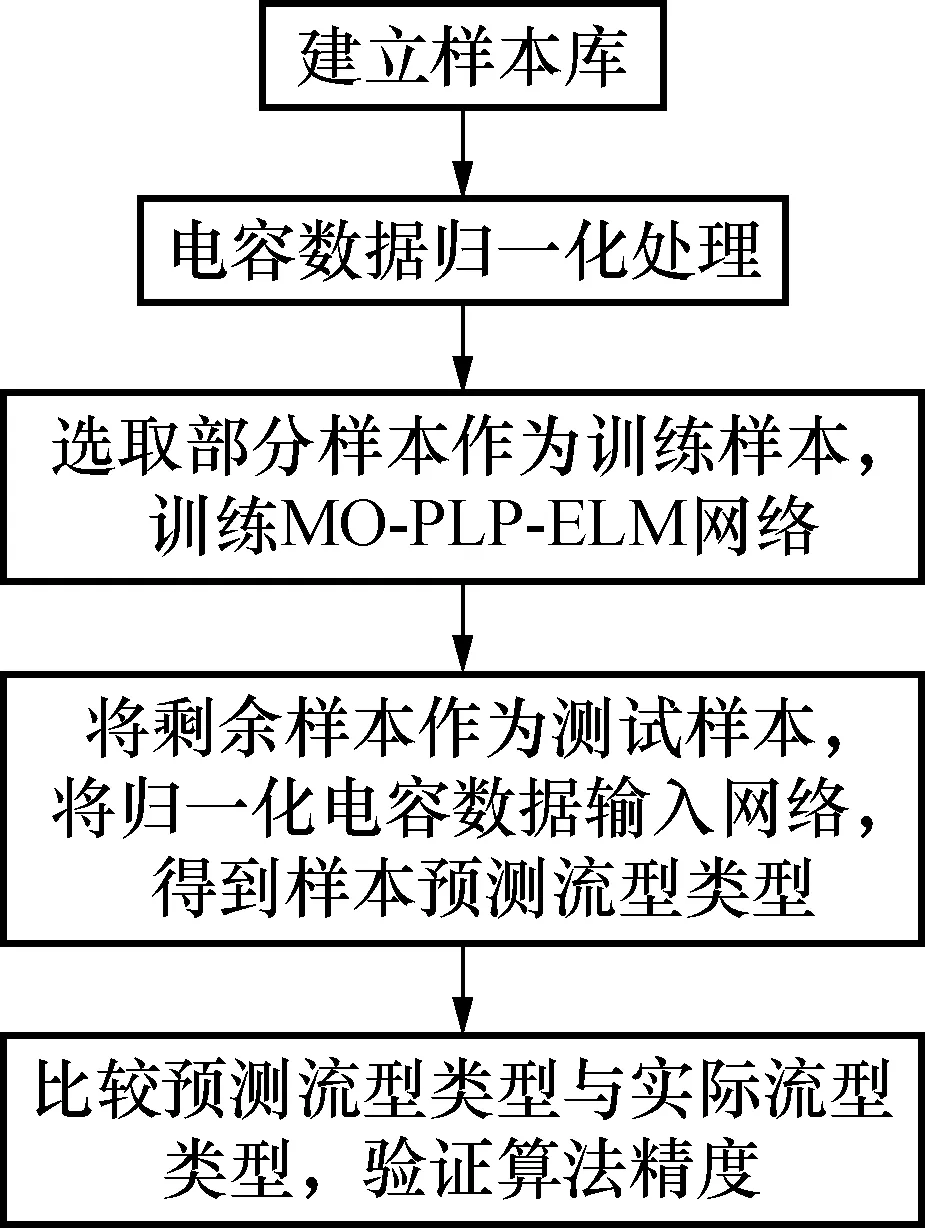
图3 MO-PLP-ELM流型辨识流程图Fig.3 Flow chart of the identification of flow pattern using MO-PLP-ELM
4 仿真实验及结果分析
4.1 仿真实验
仿真实验首先对圆形管道进行三角形剖分,如图4所示,将管内剖分为12层,共计1 728个单元,管内径设置为125 mm。
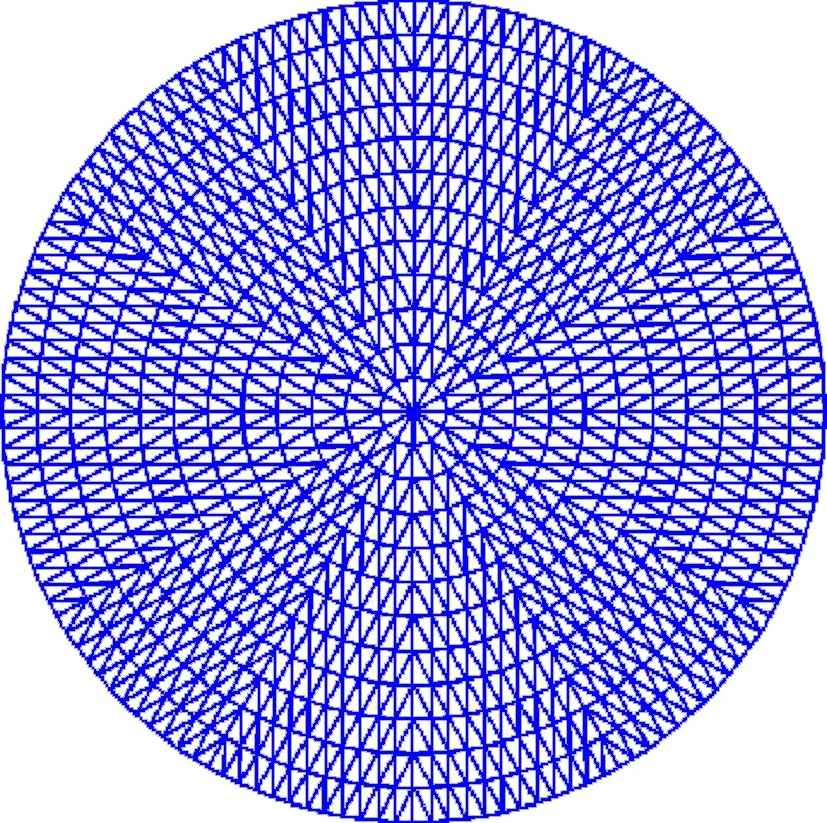
图4 管内剖分单元图Fig.4 Dissection element of the in-pipe field
本文以油/气两相流为仿真对象,油相和气相的相对介电常数分别设置为3和1。针对设置的流型,通过基于MATLAB的ECT仿真软件包进行计算得到其对应的电容值。
在进行仿真实验之前,需要先进行样本库的建立,训练样本需具有一定数量的规模和代表性,本文共建立训练样本7类,包括单个物体、2个物体、3个物体、环状、层状、空场及满场分布,如图5所示,空场及满场各50个样本,其余流型分别建立 1 000 个样本,总计5 100个样本。为使样本更具代表性,本文采用随机思想进行建模(以3个物体为例,3个圆形物体的圆心和半径为随机生成)。

图5 训练样本模型Fig.5 Phantom of training sample
仿真实验时,空场和满场各选取40个样本作为训练样本,10个样本作为测试样本外,其余5类流型均选择900个样本作为训练样本,100个样本作为测试样本。
4.2 实验结果及分析
本文选用常用的BP神经网络、支持向量机(SVM)、极限学习机(ELM)算法及PLP-ELM算法同本文使用的MO-PLP-ELM算法进行比较,其辨识结果如表1所示。

表1 各算法流型辨识率Tab.1 Identification rate of each algorithm (%)
从表1可见,MO-PLP-ELM算法辨识精度优于BP网络、SVM、ELM及PLP-ELM算法,平均辨识率可达96.1%。另外,2个物体和4个物体的辨识难度相对于常见的其它5类流型类型而言,辨识难度更高。对于2个物体的流型分布,其它4类算法的辨识结果很不理想,但本文算法辨识精度能达到97%,远优于其它4类算法。
各算法进行流型辨识的训练时间及辨识时间分别如表2所示。
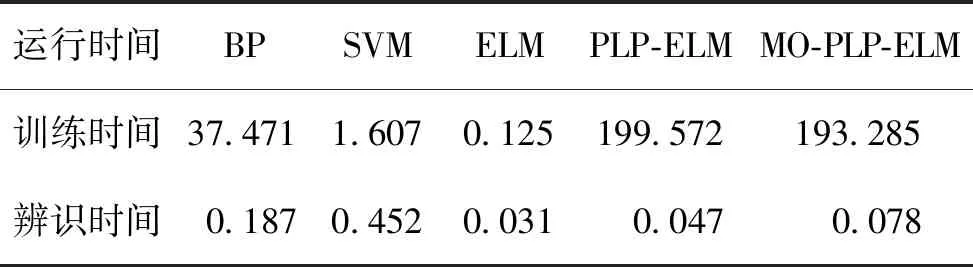
表2 各算法运行时间Tab.2 Run time of each algorithm s
由表2可见,PLP-ELM及MO-PLP-ELM算法的训练时间比其它算法高一到两个数量级,表明加入PLP算法对ELM网络的复杂度有所增加,导致其训练时间变长。在测试阶段,PLP-ELM及MO-PLP-ELM算法的辨识时间与ELM算法的辨识时间在同一数量级且均小于BP算法及SVM算法的辨识时间,可实现实时流型辨识。综上,本文采用的MO-PLP-ELM算法相较于其他算法可以得到较优的辨识结果,且平均辨识率在上述比较算法中最优,对于复杂流型辨识具有一定的参考价值。
5 结 论
本文针对7种较为复杂的两相流流型,基于电容层析成像仿真测量电容值,采用MO-PLP-ELM算法进行流型辨识,并与广泛采用的BP、SVM、ELM及PLP-ELM算法进行对比。仿真结果表明,本文使用的算法相较于其他算法对复杂流型的辨识精度更高,且更适用于复杂流型的流型在线辨识,为工业中更为复杂流体的流型辨识提出了一种新的思路。
