基于绳索欠驱动的连续型机械臂设计及仿真

郭亚星，郑继贵，侍 威，贾龙飞，陶云飞

（北京精密机电控制设备研究所，北京，100076）

0 引 言

在人类对太空的不断探索过程中，“太空垃圾”存在着潜在的威胁，“空间机器人技术”和“新型碎片主动离轨、清除与利用飞行器技术”等研究领域应运而生。连续型机械臂可实现近似连续变形，具有较多自由度；同时采用驱动系统与机械臂分离的方式，可减轻机械臂的质量，缩小机械臂的体积。因此，相关学者针对连续型机械臂的空间应用开展了一系列研究，包括连续型机械臂的基本构型，多关节结构及驱动方式，目前，都处于地面研究阶段。美国Walker根据象鼻的原理，提出一种连续型机器人，机械臂长度为83.82 cm，具有8个自由度[1,2]，但机械臂长度较小。英国OC Robotics公司在2002年已经开展对绳驱动连续型机器人的研究[3]，该类机器人应用于工业领域，主要应用于狭小空间作业，机械臂长度为1～3.1 m，最大负载可达 10 kg，但驱动数目较多，控制复杂。2018年，新松机器人自动化股份有限公司自主研发的具有（24+1）个自由度的连续型机器人，总长2269 mm，最大负载为5 kg，主要应用于狭小空间和恶劣环境，使用不同工具能够完成多种复杂作业，但也存在驱动装置体积较大、控制复杂的问题。以上研究中，单个关节至少由 3个电机驱动，若自由度过多，驱动系统体积较大，增加了控制难度。2018年，哈尔滨工业大学徐文福团队提出了一种多关节段绳索驱动柔性机械臂[4]，总长为 1265 mm，简化了驱动系统结构，减少了控制量，提高了整臂刚度和负载能力，但其机械臂长度较小。2019年，中国科学院韦贵炜提出了一种新型线驱动连续型机械臂[5]，机械臂整体有3个关节段，每个关节段包括16个小关节，最大负载能力为1.5 kg，可增加机械臂臂长，但负载能力较小。综上所述，现有连续型机械臂较难满足狭小、非结构化空间环境下长臂杆、末端大负载等要求。本文提出一种应用于连续型机械臂的新型关节组，采用欠驱动方式，简化了驱动系统结构，减少控制量，同时可实现连续型机械臂的较大臂长，在臂长一致情况下，相对单个臂杆具有更优的避障能力。

1 新型关节方案

1.1 结构及原理

按照运动不干涉原则，进行结构设计，得到SolidWorks三维模型，关节结构如图1所示。

图1 关节结构 Fig.1 Structure of the Joint

关节组由 3个关节和 3个臂杆组成，通过圆周120°均匀分布的三根驱动绳索进行驱动，如图2所示。

图2 关节组结构 Fig.2 Structure of the Joint Group

关节组内的关节相互之间为耦合联动，联动原理如图3所示[6]，借鉴带轮传动的原理，绳索交叉布置，固定在两连接点上，实现角度的传递。

图3 关节联动原理 Fig.3 Schematic Diagram of Linkage of the Joint

关节联动形式如图4所示，传动轮1至传动轮4实现关节组内关节之间俯仰自由度联动，传动轮 5至传动轮8实现关节组内关节之间偏转自由度联动，两个自由度联动都通过联动绳索1、联动绳索2实现。

图4 关节联动形式 Fig.4 Form of the Linkage of the Joint

1.2 关节组性能分析

常见的连续型机械臂方案中，单个关节由单组驱动控制，具有单个关节最大偏角。本文所提出的关节组构型，可利用一组驱动实现 3个关节的运动，关节组整体呈现为联动状态，可实现3个关节线性叠加的最大偏角。

a）等角度弯曲联动。

关节组内，当同一联动绳索连接的两传动轮直径相同，即传动轮传动比为1:1时，联动角度1α与2α相等，如图5所示。可实现两关节之间等角度运动的传递，最终呈现出等角度弯曲联动形式，如图6所示。

图5 传动比为1:1 Fig.5 Transmission Ratio of 1:1

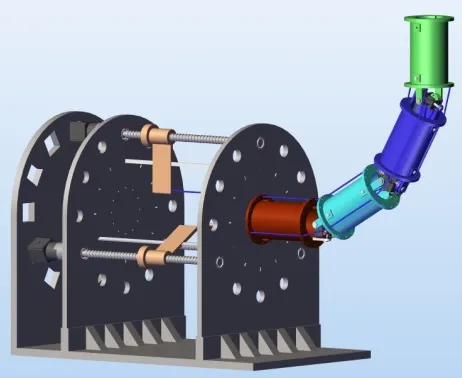
图6 等弯曲联动形式 Fig.6 Form of the Linkage of the Equal Bending

b）变角度弯曲联动。

当关节组内同一联动绳索所连接的传动轮直径不相等，即传动比不为1:1时，可实现两关节之间不同角度运动的传递，如图7所示，3个关节可表现为不同的运动角度，实现关节非等角度联动的运动模态。

图7 传动比不为1:1 Fig.7 Transmission Ratio is not 1:1

2 运动学分析

2.1 运动学建模

连续型机械臂关节组坐标系如图8所示。单个关节组内的关节转角互相耦合，角度值与方向相等，单个关节组内每个关节处的角度变量相等，单个关节具有2个旋转自由度，分别为绕X轴旋转ψ角，绕Y轴旋转θ角。

图8 关节组坐标系 Fig.8 Coordinate of the Group of Joints

相邻坐标系间的相对位置和姿态可通过基本的平移变换Trans和旋转变换Rot得到，在公式中分别采用T和R表示。

坐标系{0}到坐标系{1}的变换矩阵如式（1）所示，先沿Z0轴平移l和d，绕X1轴旋转ψ角，再绕Y1轴旋转θ角：

坐标系{i-1}和坐标系{i}之间的变换矩阵转换过程为，先沿Zi轴平移l和 2d，绕Xi轴旋转ψi角，再绕Yi轴旋转θi角：

式中sψ=sinψ，cψ=cosψ，sθ=sinθ，cθ=cosθ。

单个关节组齐次变换矩阵为

图9 关节运动参数描述 Fig.9 Description of Motion of the Joint

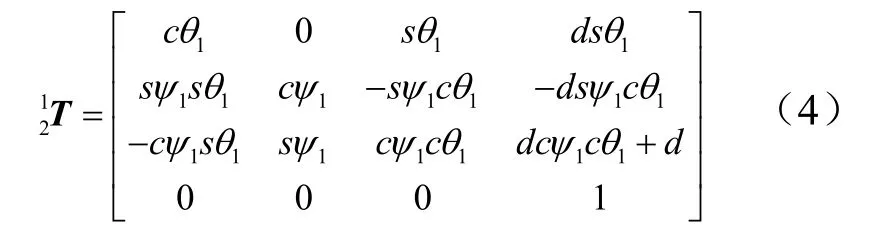
单个关节实现互相正交的两个自由度运动，至少需要3根驱动绳索耦合驱动。本文设计采用联动关节组模块，单个联动关节组内关节的运动互相耦合，运动状态一致，即关节角度变化与关节处驱动绳索长度都相等，因此关节之间的运动耦合可转化为关节组之间的运动耦合，只需将单个关节的运动变化进行线性叠加。

本文采用联动关节组形式，关节组内的关节运动角度相同，在进行运动学分析时，关节组内3个关节的同一个方向的角度变量可取同一个值，与传统连续型机械臂相比，减少了实际控制过程中的控制变量，简化了控制程序的复杂度。

2.2 运动学仿真

连续型机械臂工作空间反映末端能到达的位置，根据关节空间到操作空间的正运动学映射，选取关节角度θ、ψ范围都为[-30°，30°]，臂杆长度L为180 mm，关节一半长度d为35 mm，利用蒙特卡洛法对关节角度随机取值，最终得到连续型机械臂对应单个关节组和4个关节组时，末端执行器的工作空间，如图10所示，中间深色部分为单个关节组，外围为4个关节组。通过末端工作空间范围，可确定连续型机械臂极限运动范围。

图10 连续型机械臂工作空间 Fig.10 Workspace of the Continuous Manipulator

取关节俯仰角θ线性变化，变化范围为[-30°，30°]，取关节偏转角为0，借助Matlab绘制准连续型机械臂在不同关节角度下的轨迹状态，如图11所示。从图11中可以看出，在不同角度状态下，连续型机械臂呈现出不同的运动状态。同时针对单个关节和关节组进行了工作空间对比分析，如图12所示。通过对比分析，可以看出采用欠驱动关节组形式，与传统连续型机械臂相比，在实现相同的自由度时，单个关节组等效于 3个关节的叠加，连续型机械臂的可达范围更广，增加了连续型机械臂的工作空间，增强了末端的运动灵活性，且整臂的连续运动更平滑。

图11 关节组形式的不同运动状态 Fig.11 Different States of the Form of Joint Groups

图12 关节形式的不同运动状态 Fig.12 Different States of Form of Joints

3 静力学分析

本文以静力矩平衡原则进行连续型机械臂静力学建模与分析，并基于以下假设：

a）忽略驱动绳索的摩擦力；

b）单根驱动绳上的拉力均匀分布，处处相等；

c）将驱动绳索拉力看作外力进行分析。

本文所设计的连续型机械臂，在水平伸直状态下，驱动绳索的拉力最大，机械臂本体各部分对本体根部的力臂最大，因此静力学分析选取水平伸直状态下的连续型机械臂进行分析，力学简化模型如图13所示。

图13 力学简化模型 Fig.13 Simplified Model of Mechanics

表1 参数描述Tab.1 Description of the Parameters

a）机械臂整体受力分析。

机械臂整体相对X轴的力矩为

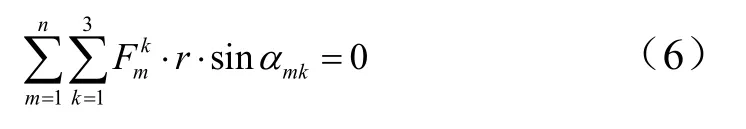
机械臂整体相对Y轴的力矩为

b）任意关节组q受力分析。

关节组q相对X轴的力矩为

关节组q相对Y轴的力矩为

其中，Lq= （n-q+ 1 ）Ln。

第q个关节组的驱动绳索拉力为

驱动绳索拉力的求解为2个公式，3个未知量，属于不定方程组，需增加额外约束条件，选取3根驱动绳索拉力之和最小为约束条件，构建最优化函数来进行驱动绳索拉力的求解，最优化函数为

根据连续型机械臂的实际参数需求，通过上述最优化函数求解，可得出驱动绳索拉力的最大值Fmax，进一步可确定试验所需驱动绳索的规格。本文在进行静力学分析时，由于关节组内部的关节相互之间靠联动绳索耦合，因此将每个关节组作为一个整体模块，为后续的动力学分析奠定基础。

4 结束语

本文提出一种应用于连续型机械臂的新型关节，并进行了结构设计、运动学分析及仿真研究。相比传统连续型机械臂，采用欠驱动联动关节组形式的连续型机械臂，具有以下特点：a）采用欠驱动方式简化了驱动系统结构，简化了控制量；b）采用联动关节组形式，与传统连续型机械臂相比，在实现相同的自由度时，连续型机械臂的可达范围更广，增加了连续型机械臂的工作空间，增强了末端的运动灵活性，且整臂的连续运动更平滑；c）本文提出的结构，可通过改变传动轮的直径，实现等弯曲和不等弯曲两种联动形式。通过对机械臂进行运动学分析与仿真，得出其运动规律，为后续零部件的设计选型与试验验证提供坚实的理论基础。