运筹学整数规划在体育赛事人员问题中的研究

周德康

(浙江省之江棋院，浙江 杭州 310004)

运筹学作为一门近代新兴学科，起始于第二次世界大战期间英国和美国军事管理部门进行的军事问题的研究。第二次世界大战后，运筹学在管理中的运用越来越被企业管理者们和政府部门所认识，如利用运筹学方法来解决新型的制定计划、进行决策的管理问题。近年来，在数学和计算机科学技术的巨大推动力作用下，目标规划、图论网络、存贮论、对策论和排队论等运筹学分支研究范式日趋成熟，应用领域不断扩大，成为由多学科融合创新形成的发展最快的学科之一。[1]

在体育学学科发展的理论和实践中，运筹学具有重大的影响力，学科之间相互交叉体现出覆盖面广、注重实战和普遍适用的前景与趋势。对策论是运筹学的一个重要分支，研究的对象是具有竞争或对抗性质的行为，与体育领域有着密切关联，处理问题的方法又有着明显特色，已经日益引起学界的广泛关注。整数规划是运筹学的另一个重要分支，研究的对象是许多实际状况中要求变量取整数解的问题，采用分支定界法求解，多应用于人数、车数、机器的台数以及方案的取舍等。[2-3]

对于大部分的体育赛事，基于时间和资源混合的关键约束是决策的最终考虑因素。体育赛事人员安排是赛事实施过程中人力资源可用性约束的管理，在合理编制最优资源计划程序中，运筹学整数规划有时被用来作为解决问题的最佳方法。利用计算机科学和计算机技术的成就，根据赛事目标的规定，对赛事工作的各项人力资源活动作出周密的安排。围绕赛事目标的完成，系统地确定赛事任务、安排任务进度、编制完成任务所需的人力资源预算等，能够保证赛事在合理的期间内，用尽可能低的成本和尽可能高的质量完成。[4-5]

1 基础模型的建立

体育赛事人员安排是一个实际问题，科学的人员安排不但可以保证赛事按时完成，而且可以使赛事达到其预设的目标，确保赛事在批准的预算内完成，这既是赛事管理的一大职能，也是赛事实施的基础。[6]

随着体育赛事日益增多，经济效益和社会效益的双赢导致许多体育组织培养了一批专业的竞赛主管。体育组织高绩效工作系统与竞赛主管人才管理发展到现在，单纯地追求传统人力资源管理的时代已经过去，目前面临的是通过胜任素质来应对决策需要的战略性人力资源管理。体育组织在招聘选拔、培训开发、绩效管理、梯队建设和文化落地等方面，构建与应用维度、行为等级协调统一的胜任素质模型，改善竞赛主管人力资源管理体系。以可持续和可预测的行为方式，体现高绩效的综合特质的竞赛主管，既是体育组织战略执行的关键，又是体育赛事高绩效的引擎。一个优秀的竞赛主管是体育赛事人员安排的前置条件。[7]

在体育赛事人员安排问题中，运筹学整数规划是一类很特殊的规划模型，其全体变量取值只为0或1逻辑变量，只能解决参与或不参与的问题，具有局限性，表现出一定的不足。运筹学的另两个重要分支网络计划技术和动态规划提供了整体解决方案：通过网络计划技术，使用工作分解结构工具，对体育赛事工作由粗到细的分解，形成分级的树型结构，依据各组成要素之间逻辑关系及完成时间，绘制网络图；通过动态规划，把比较复杂的体育赛事问题转换成确定型的多阶段问题，竞赛主管胜任或不胜任的状态随阶段变更而变化，然后对离散性问题，一个一个地进行求解。至此，回归到整数规划可以解决的问题。

浙江一家体育发展有限公司人力资源部安排一些竞赛主管完成A、B和C3个赛事。赛事A、B和C分别需要12、18和30人用1个月来完成。竞赛主管甲、乙、丙和丁都可以完成这些赛事，他们的月薪分别是10 600元、12 200元、12 900元、15 700元。

根据模型边界条件提出假设：①赛事：在整个过程中不出现大的调整；各项条件均满足各项限制；管理中不出现重大变故；②竞赛主管：在一定时期内完成相同的任务；在面对不同的任务时完成时间相同。模型内生变量中，Z表示赛事的总薪酬，tij(i=1，2，3；j=1，2，3，4)t表示月数，i表示赛事，j表示竞赛主管。赛事和竞赛主管之间的时间关系，如表1所示。

表1 赛事和赛事主管的时间关系

完成3个赛事的总薪酬，等于竞赛主管甲、乙、丙和丁参与完成赛事A、B和C各所用的月数和月薪酬的乘积之和，可以表示为：10 600(t11+t21+t31)+12 200(t12+t22+t32)+12 900(t13+t23+t33)+15 700(t14+t24+t34)；

赛事A完成所需的时间约束为：t11+t12+t13+t14≥12；赛事B完成所需的时间约束为：t21+t22+t23+t24≥18；赛事C完成所需的时间约束为：t31+t32+t33+t34≥30。[8]

综上所述，我们得线性规划模型如下：

目标函数：

约束条件：

这是一个整数规划优化问题，对变量有整数约束，一般不能使用单纯形法，采用LINGO能够较容易地求解，具体的程序如图1。[9]

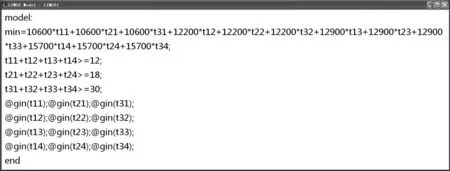
图1 LINGO模型窗口中显示的整数规划程序图

运行程序输出结果。图2当前模型的类型为纯整数线性规划，当前解的状态表示已经达到全局最优解，当前解的目标函数值为636 000，使用的特殊求解程序分支定界算法，变量数量总数12整数变量数，约束数量总数为4，非零系数数量总数为24。

图2 LINGO状态窗口图

据图3输出结果可知：找到全局最优解，目标值为636 000.0，各变量的值：T11=12.00000，T21=18.00000，T31=30.00000，给出检验数、松弛变量和对偶价格的值。

图3 LINGO报告窗口图

整理相应的运行结果如表2，总薪酬最小为：Zmin=636 000.0。

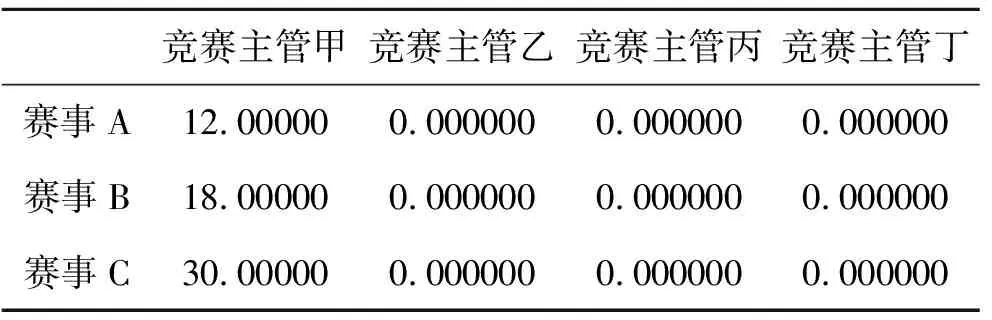
表2 结果数据表1

通过模型计算结果可以看出，竞赛主管甲工作于赛事A、B和C是最优解。其中的原因，是竞赛主管甲的月薪最低，所有的赛事都由其完成，可以让总薪酬降到最低。因此，模型在逻辑上正确，符合实际情况，可以作为进一步研究的基础。

现实的赛事管理工作中，启动、规划、执行、监控和收尾各个阶段都面临着诸多不确定性，在实施过程中又常常面临范围、质量、进度、预算、资源和风险等多重具体的制约因素的干扰。只有逐步考虑各种复杂因素问题，由数学数据去分析在各种情况下人员分配的最优解，模型才具有实用性。[10]

2 模型的扩展

在体育组织中，成功的赛事管理有时间、成本和绩效三约束，这与内部条件和外部环境密切相关。组织的结构和对人员配备的关注度为赛事管理提供了背景，它们既能起到支持与促进的作用，也可能妨碍赛事正常运作。大多数体育组织的业务范围是健身指导和竞赛表演，所采用的常见结构类型是矩阵型——一个职能部门与项目部门双重的层级。对赛事管理而言，组织环境是复杂的、动态的，有多种运营形式的需要，存在机会多而资源少的挑战。因此，竞赛主管是一个领导密集型的职业，在赛事实施中发挥核心作用，他们需要大量的时间来协调赛事和部门之间对关键资源的共享。[11]

2.1 赛事的进度约束和组织约束

增加模型边界条件：根据资源估算的结果，A、B和C3个赛事要求在18个月内完成。为确保履行职责、开展工作的连续性、稳定性和有效性，通常竞赛主管在每6个月中只安排1个赛事。

3个赛事要求只能在18个月内完成，则竞赛主管甲、乙、丙和丁各自的工作时间都不超过18个月：

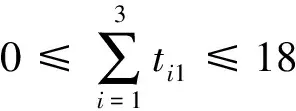
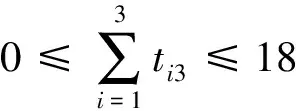
因为竞赛主管在每6个月中只能被安排一个赛事。

表3中，aij，bij，cij，dij(i=1，2，3；j=1，2，3)，a，b，c，d表示竞赛主管甲、乙、丙和丁，i表示赛事，j表示时期。aij，bij，cij，dij=0表示竞赛主管不被安排赛事；aij，bij，cij，dij=1表示竞赛主管被安排赛事。

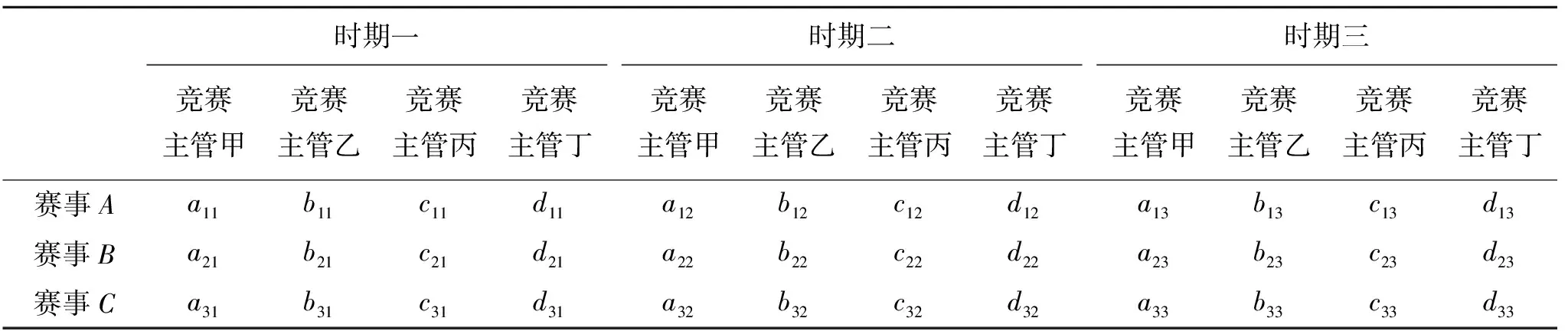
表3 赛事的进度和组织约束关系

竞赛主管甲、乙、丙和丁在时期一、时期二和时期三，各阶段都有可能被安排参与赛事，则：

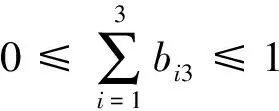
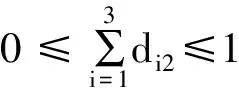
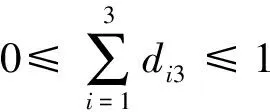
竞赛主管们在1个时期内参与1个赛事，薪酬应按6个月来计算，则每位竞赛主管时期一、时期二和时期三的所用时间之和为工作于1个赛事所用的总时间，有：

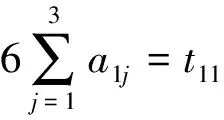
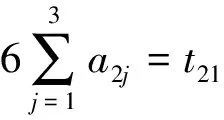
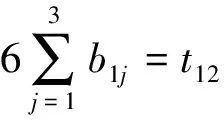
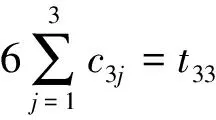
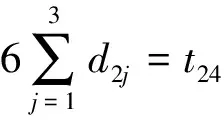
综上所述，建立相应的数学模型，增加约束条件如下：

约束条件：

S.T.

编写LINGO程序求解，运行程序输出结果，Z=736800.0，整理输出结果如表4和表5所示。[12]

表4 运行程序输出结果1

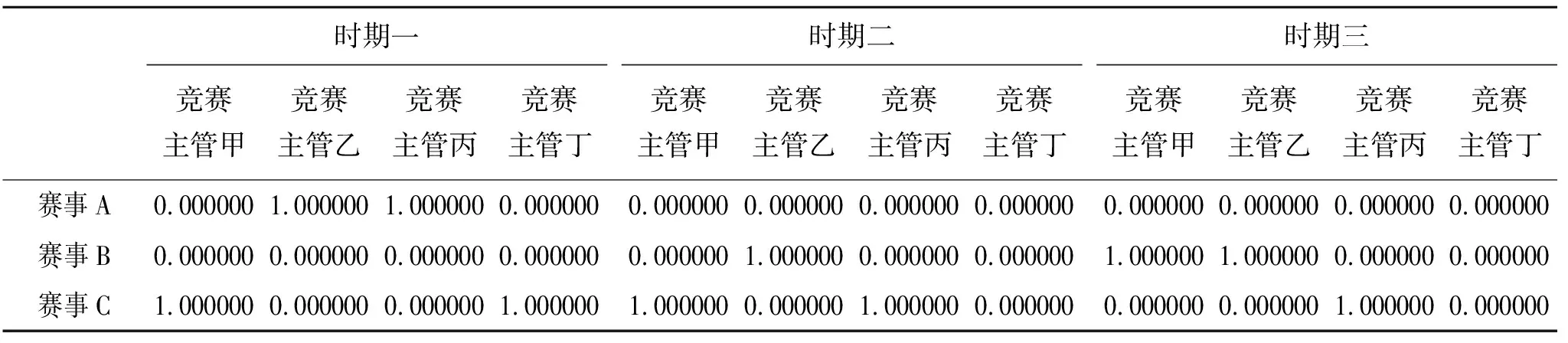
表5 运行程序输出结果2

由于赛事的进度约束和组织约束，竞赛主管乙、丙和丁被安排参与赛事，因此总薪酬增加。

2.2 赛事的赶工约束和冲突约束

增加模型边界条件：为了推动体育竞赛表演业跨越式发展，赛事A和B入库《重点培育品牌体育赛事名录库》，要求能够在12个月内完成。由于个人工作风格的差异，竞赛主管甲和乙存在个性冲突，意见分歧成为负面因素，致使他们不能同时在1个赛事中工作。

赛事A和B在12个月内完成：

6(a11+b11+c11+d11+a12+b12+c12+d12)≥12

6(a21+b21+c21+d21+a22+b22+c22+d22)≥18

竞赛主管甲和乙在时期一、二和三里不能同时出现：

0≤a11+b11≤1 0≤a21+b21≤1

0≤a31+b31≤1

0≤a12+b12≤1 0≤a22+b22≤1

0≤a32+b32≤1

0≤a13+b13≤1 0≤a23+b23≤1

0≤a33+b33≤1

增加这些约束条件：

约束条件：

S.T.

6(a11+b11+c11+d11+a12+b12+c12+d12)≥12

6(a21+b21+c21+d21+a22+b22+c22+d22)≥18

0≤aij+bij≤1(i=1，2，3j=1，2，3)

编写程序，由程序运行结果可得Z=757 800.0，整理输出结果如表6和表7所示。

表6 程序运行结果1

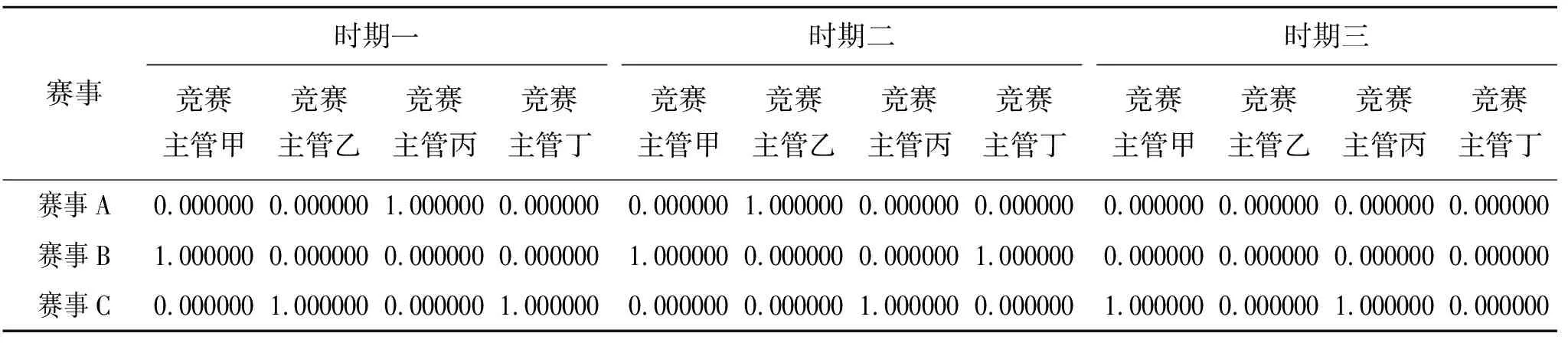
表7 程序运行结果2

赛事的赶工约束和冲突约束将会给人员安排带来额外损失。对于赶工约束，可以采用快速跟进的方法，把正常情况下按顺序执行的活动或阶段并行执行，来缩短赛事期间。对于冲突约束，可以采用妥协合作的方法，综合考虑不同的观点和意见，寻找能让全体当事人都在一定程度上满意的方案，引导各方达成一致意见并加以遵守。

3 结论

本文以体育赛事人员安排问题为背景，在综合数学建模方法和软件应用的基础上，针对人员安排的计算展开讨论，设定了一些常量和决策变量对问题中的已知和求解结果进行表示，利用规划模型进行人员安排问题的求解。求解完成所有赛事所需总薪酬的最小值的人员分配方案后，再考虑进度、组织、赶工和冲突的问题，对约束进行合理的转换，然后运用LINGO软件对模型进行求解，讨论了这些因素对总薪酬的影响，最终得出赛事的人员安排。

基于运筹学整数规划的体育赛事人员安排模型，可以结合人力资源负荷图，研究比赛期间约束下的人力资源均衡问题。对于劳动力来说，人力资源的成本将随着雇佣人数和培训人员的需要而增加。在赛事的人力资源需求中，为了使各工作人力资源需求的波动最小，应对竞赛主管进行再次分配，使其能够以比较稳定的人力资源使用率来降低人力资源成本。