弹性壁扩张式消声器传递损失特性研究

侯九霄，朱海潮，毛荣富，袁苏伟

（海军工程大学船舶振动噪声重点实验室，武汉430033）

0 引 言

扩张式消声器广泛应用于船舶管路系统，实际工程中受空间尺寸限制，其低频吸声效果有待提高。挠性接管具有较大的位移补偿能力和优良的隔振性能，前期研究主要集中在平衡性能[1-2]和振动传递特性[3-4]。张维等[5]试验研究发现，挠性接管在中低频段对线谱和宽频带噪声都有一定的消声效果。陈刚等[6]推导了挠性接管对管内声传播速度的影响。对鼓型消声器[7-8]和板式消声器[9-11]的研究表明，利用声波和弹性管壁的耦合作用，使管路内的声阻抗不连续而发生反射和散射作用，能够降低下游的透射声能。因此，将挠性接管和管路消声器相结合，研究弹性壁扩张式消声器传递损失特性，对于抑制船舶管路系统噪声的传播具有重要意义。

为此，本文提出弹性壁扩张式消声器结构模型，利用传递矩阵法将其划分为三个声学单元，基于模态叠加法和Kirchhoff-Helmholtz 积分公式建立弹性壁管段的结构-声耦合模型，利用Fourier-Galer⁃kin 方法进行耦合方程的求解，推导出弹性壁扩张式消声器的传递损失特性，并与传统刚性壁扩张式消声器进行比较，进一步地分析管壁参数对消声性能的影响，并利用有限元法对理论结果进行验证。此外，本文还提出弹性壁扩张式消声器的等效流体模型，简化了传递损失特性的求解方法。

1 弹性壁扩张式消声器理论

1.1 传递矩阵模型

弹性壁扩张式消声器的模型如图1（a）所示，挠性接管构成了消声器的腔壁。上下游管道的半径为a，扩张腔的半径为b，长度为L。在入射平面波pi作用下，反射声波为pr，透射声波为pt。考虑到模型为轴对称结构，在入射平面波作用下，弹性管壁的响应和内部声场成轴对称分布。此时，三维模型可以简化为二维轴对称结构如图1（b）所示。

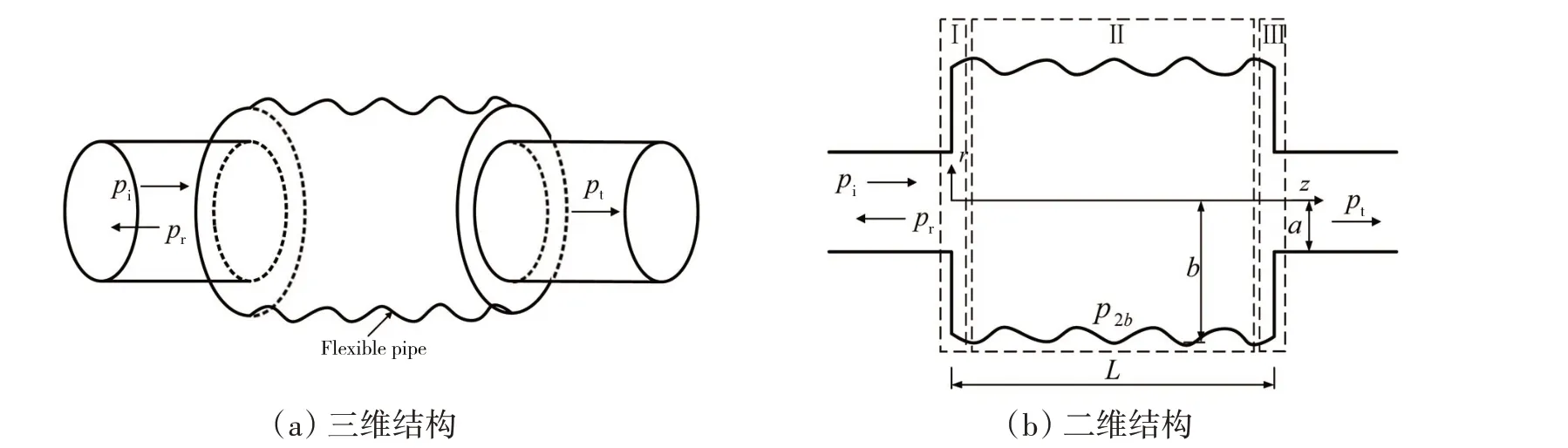
图1 弹性壁扩张式消声器结构示意图Fig.1 Geometry of the expansion muffler with flexible walls

利用传递矩阵法将弹性壁扩张式消声器划分为I、II和III三个声学单元。设声学单元I和III的传递矩阵分别为T1和T3，

式中，

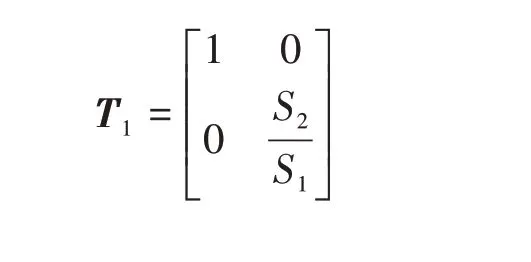
1.2 弹性管壁的振动响应

圆柱形的弹性管壁在入射声场p2i激励作用下产生动态响应，由于结构和入射声场具有轴对称性，因此弹性管壁的响应也成轴对称分布。为书写简便，下文中统一省略时间项ejωt。

依据Donnell-Mushtari薄壳理论，弹性管壁的轴对称运动微分方程为

弹性管壁的两端为简支边界条件，利用模态叠加法，弹性管壁的速度响应可表示为

利用Fourier-Galerkin方法求解弹性壁的运动微分方程，还需要求解弹性管段内部的辐射声压p2。

1.3 辐射阻抗

对于声学单元II，管道内部的Green函数为

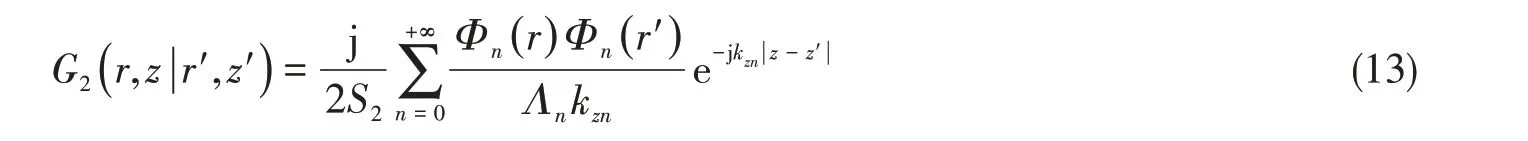
式中，( r,z )为观察点坐标，( r',z' )为源点坐标，Φn( r )、Λn和kzn分别为第n 阶特征函数、模态质量和轴向波数，

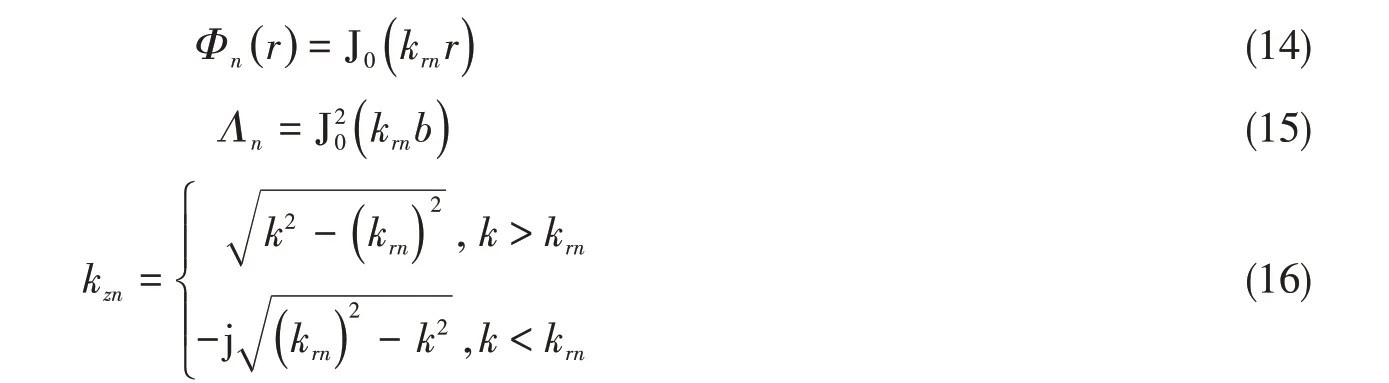
式中，Ji( krnr )为i阶柱贝塞尔函数；krn为径向模态波数，满足J1( krnb )= 0。

利用Kirchhoff-Helmholtz积分公式，可得II空间的声压分布为

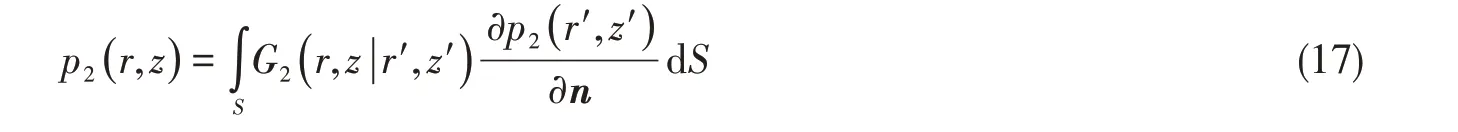
式中，n为弹性管壁的外法线方向。

将式（7）、（13）代入式（17），得

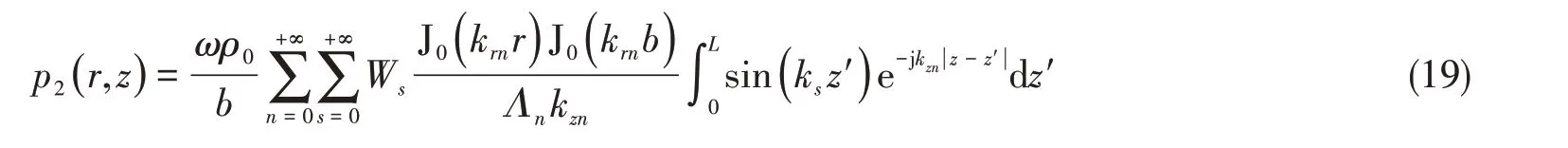
令r=b，求得弹性管壁位置的声压为

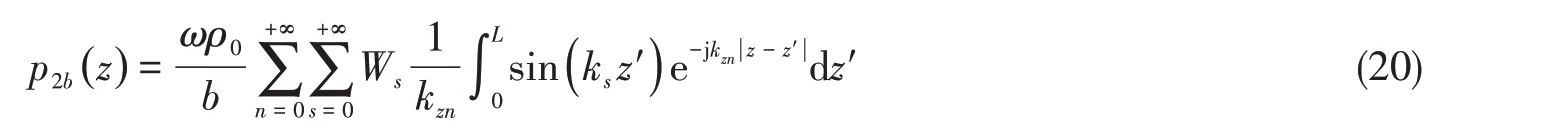
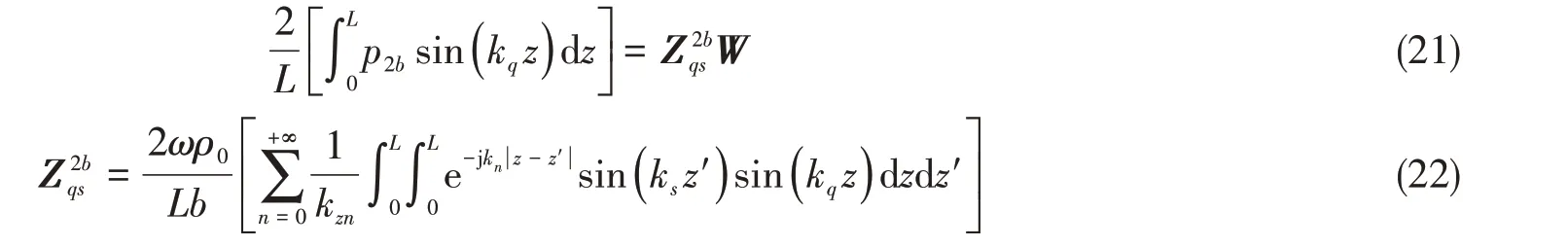
1.4 耦合方程求解和管内声场

将公式（22）代入式（9），得

求得弹性管壁的响应为

可得管内流体的质点振速uII为

1.5 传递损失

则声学单元II的传递矩阵T2为

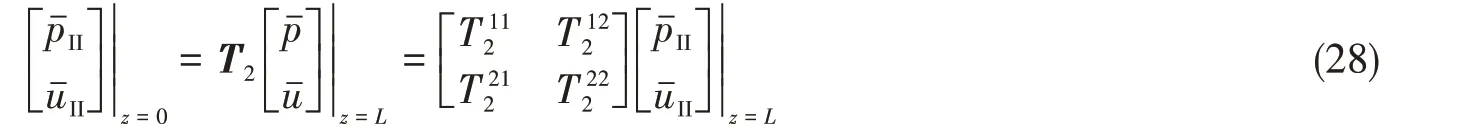
式（28）包含四个未知量和两个方程，还需要另外两个条件才能求解。由于声学单元II 具有结构对称性，依据互易原理可得

联立式（28）～（29）可得声学单元II的传递矩阵为

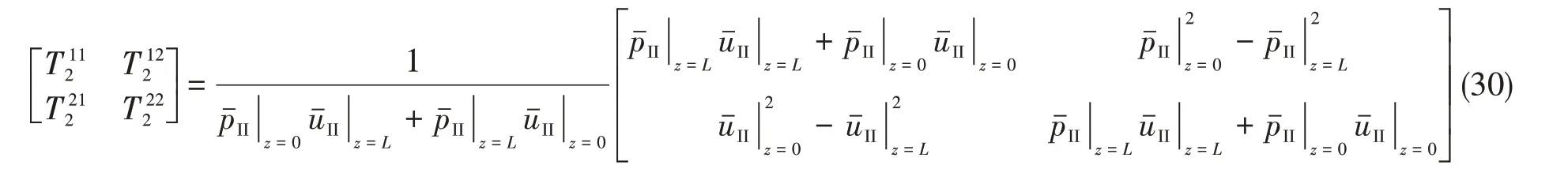
进一步地，得到弹性壁扩张式消声器入口到出口的传递矩阵T为

求得弹性壁扩张式消声器的传递损失为

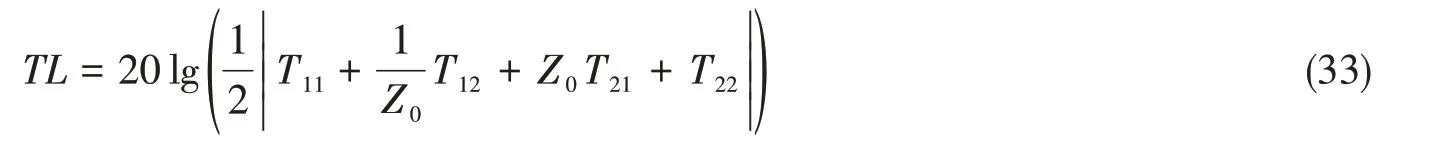
2 理论模型的验证

2.1 模态数目截断收敛性验证

利用模态叠加法求解弹性壁扩张式消声器传递损失，在实际计算过程中，分别截取前M阶的结构模态和前N阶的管道声模态。为确保求解结果的精确性，需要对模态数目截断收敛性进行验证。设置弹性壁扩张式消声器的几何参数与材料属性如表1所示。

以前50 阶结构模态和管道模态计算结果为准，构建模态截断误差函数为

表1 弹性壁扩张式消声器的几何参数与材料属性Tab.1 Structural parameters and material properties of flexible expansion muffler

式中，[ f1,f2]为频率范围，本文主要关注[ 20,2 000 ]Hz 频率范围内的弹性壁扩张式消声器的传递损失特性。取M=N，得到模态截取误差随截断模态阶数的曲线如图2 所示，随着模态数目的增加，模态叠加法求解结果趋近一致。当模态阶数大于8 时，所得结果误差已经小于1%。综合考虑计算成本，本文在计算弹性壁扩张式消声器传递损失时均选取前10阶模态叠加的结果。

2.2 有限元验证

为验证本文理论的准确性，利用有限元方法对理论结果进行验证，选用COMSOL Multiphysics 中声-壳耦合模块，在结构和声场耦合面上满足压力连续和法向振速连续条件。求得弹性壁扩张式消声器的传递损失曲线的理论结果与有限元结果如图3所示。对比发现，在中低频范围内，理论结果和有限元结果吻合良好；在高于1 500 Hz频率范围内理论结果与有限元仿真结果在幅值上有些许偏差，原因在于前文所使用传递矩阵法为平面波假设条件，在高频范围内弹性壁扩张式管路消声器中产生高次波，因而基于平面波假设的求解结果会带来一定的偏差。

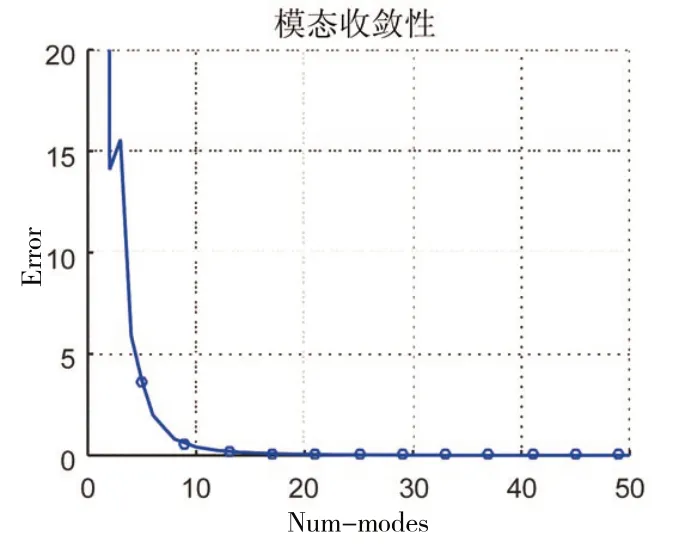
图2 模态数目截断误差曲线Fig.2 Convergence of transmission loss with different numbers of modes

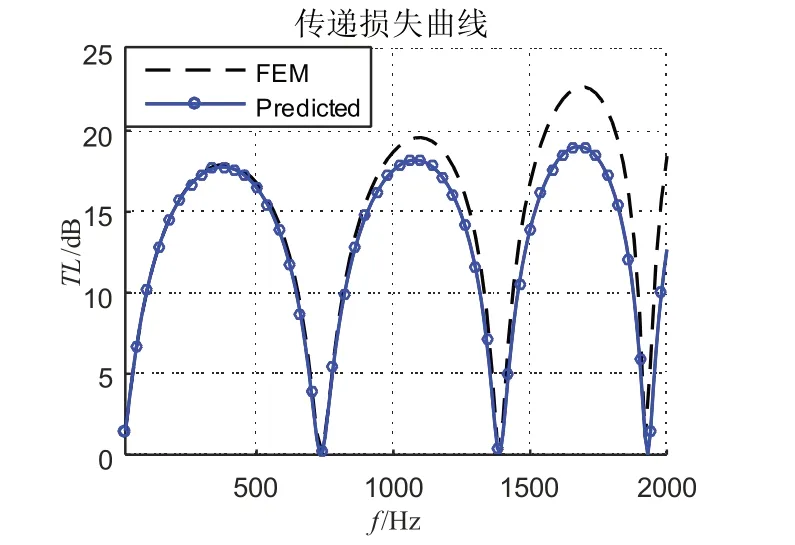
图3 理论结果与有限元计算结果的对比Fig.3 Comparison of transmission loss between theoretical results and FEM results

图4 为采用有限元方法计算得到的在1 400 Hz 弹性壁扩张式消声器内声场的切片图，此时，管道内出现高次波的传播形式。

2.3 与刚性扩张式消声器的对比

在相同尺寸条件下，对比弹性壁扩张式消声器与现有的刚性扩张式消声器消声特性，设置弹性壁扩张式消声器的几何参数与材料属性如表1所示。对比弹性壁扩张式消声器与现有的刚性扩张式消声器的传递损失曲线如图5所示。

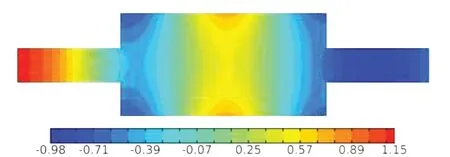
图4 1 400 Hz弹性壁扩张式消声器内部声压云图Fig.4 Sound pressure in expansion muffler with flexible walls at 1 400 Hz

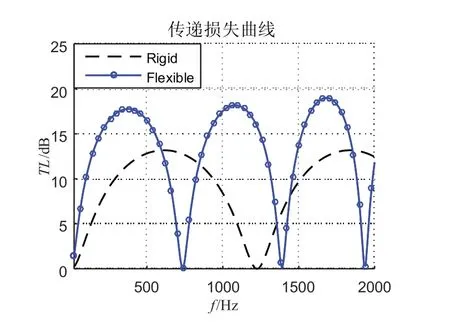
图5 弹性壁扩张式消声器与刚性扩张式消声器的对比Fig.5 Comparison of TL between flexible and rigid expansion mufflers

可以发现，相较刚性壁扩张式消声器，弹性壁扩张式消声器的传递损失曲线的峰值得到了提高。同时，通过频率向低频移动，低频消声性能得到了提升。

3 弹性管壁参数的影响

3.1 弹性模量

选取管壁材料的弹性模量分别为E1=10 GPa、E2=30 GPa 和E3=210 GPa，密度为ρ=1 200 kg/m3，得到不同弹性模量对弹性壁扩张式消声器传递损失的影响如图6 所示。可以发现，随着弹性模量的降低，弹性壁扩张式消声器的传递损失曲线进一步地向低频移动。由此可见，管壁采用挠性接管以后，并且选用较小的弹性模量，对于提高扩张式消声器的低频消声器性能有利。

3.2 密度

选取管壁材料的密度分别为ρ1=1 200 kg/m3、ρ2=2 700 kg/m3和ρ3=7 800 kg/m3，弹性模量为E=30 GPa，得到密度对弹性壁扩张式消声器传递损失的影响如图7 所示。可以发现，增大管壁材料的密度会使弹性壁扩张式消声器传递损失曲线向低频方向移动，然而，对低频消声性能影响不大。

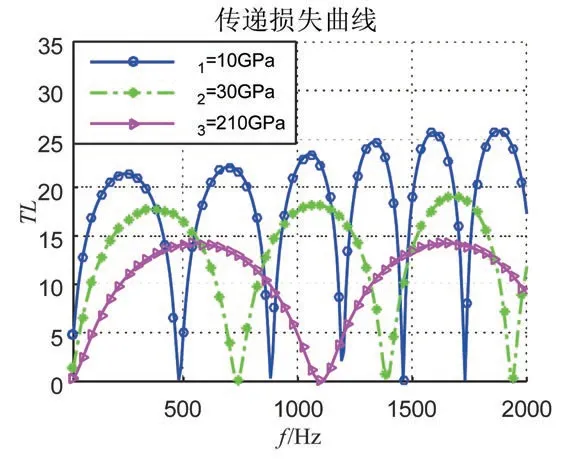
图6 管壁弹性模量对消声器传递损失的影响Fig.6 Influence of elastic modulus of the flexible pipe on transmission loss

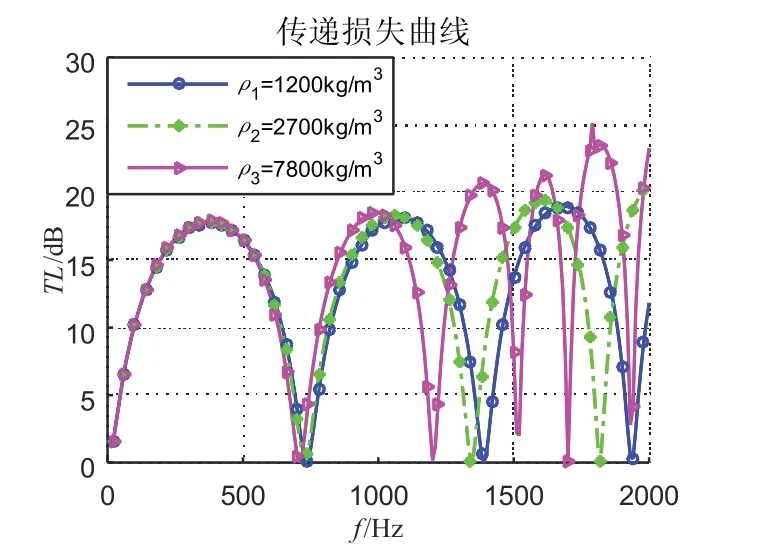
图7 管壁密度对消声器传递损失的影响Fig.7 Influence of density of the flexible pipe on transmission loss

3.3 阻尼

实际中弹性管壁为有阻尼结构，此时，用Lηs2替代原有的背腔结构特征参数Ls2，

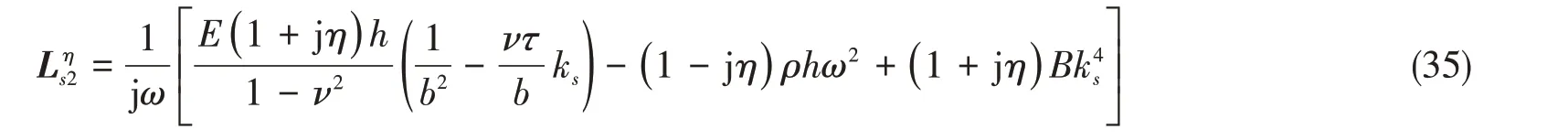
选取管壁材料的弹性模量为E=30 GPa，密度为ρ=1 200 kg/m3，对比不同阻尼系数对弹性壁扩张式消声器传递损失的影响如图8 所示。可以发现，随着阻尼系数的增加，弹性壁扩张式消声器在通过频率处的传递损失得到了提高，对于提高消声器宽频范围的消声性能有利。

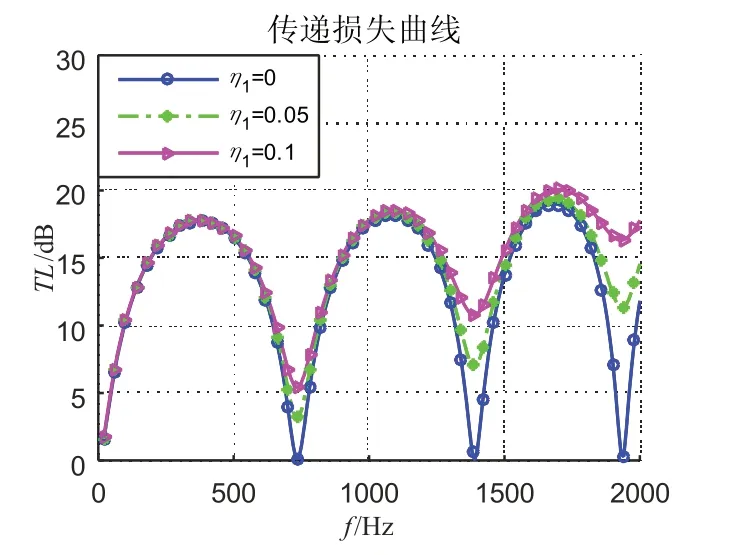
图8管壁阻尼对消声器传递损失的影响Fig.8 Influence of damping factor of the flexible pipe on transmission loss

4 等效流体模型

前文基于Green 函数和Kirchhoff-Helmholtz 积分公式，得到弹性壁扩张式消声器的传递损失。为简化计算，根据文献[6]对挠性接管内等效声速的计算方法，忽略管壁的振动，将声学单元II近似为内部充有声速为ce的等效流体介质的直管段。依据Korteweg波速公式，声学单元II的流体等效声速为

式中：c0为自由空间水介质中的声速；K=2.06×109Pa 为水介质的体积弹性系数；C 为修正系数，在两端均为弹性支撑条件下，C=1。此时，声学单元II的等效传递矩阵为

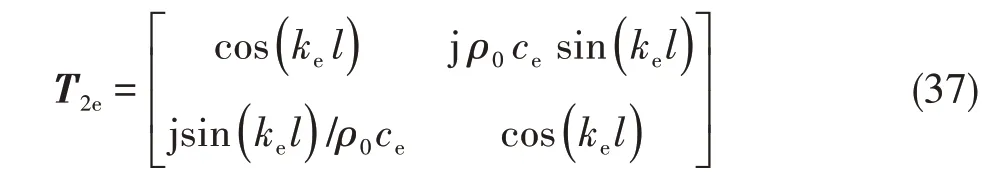
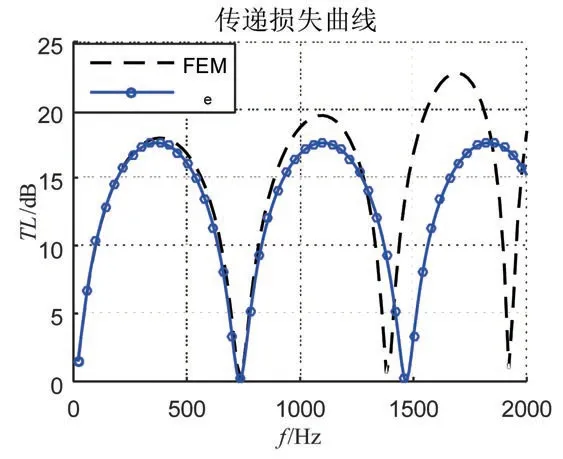
图9 等效流体法与有限元计算结果的对比Fig.9 Comparison of TL between equivalent fluid method and FEM results

式中，ke= ω/ce。将式（37）代入式（32）得到整个弹性壁扩张式消声器的传递矩阵，联立式（33）可以得到采用等效流体模型法弹性壁扩张式消声器的传递损失。

同样选用表1 所示的几何参数与材料属性，采用等效流体模型法得到弹性壁扩张式消声器与有限元仿真结果如图9所示。可以发现，在低频范围内，等效流体模型法和有限元法结果吻合良好；在800 Hz以上范围内等效流体模型结果偏差较大，原因在于等效流体法虽然考虑了管壁弹性对管内介质声速的影响，却没包含有限长管壁结构振动的影响。不过，在低频范围分析时等效流体法在取得满意精度的同时，极大简化了求解过程。

5 结 论

本文提出了弹性壁扩张式消声器结构模型，采用传递矩阵法将圆形管道弹性壁扩张式消声器分为三个声学单元，基于Green 函数和Kirchhoff-Helmholtz 积分公式建立其声学理论模型，并研究了管壁参数的影响。基于等效流体模型，得到弹性壁扩张式消声器传递损失的近似解法。利用有限元法对理论结果进行了验证，得到以下结论：

（1）相较传统刚性壁扩张式消声器，弹性壁扩张式消声器传递损失曲线的峰值得到了提高，同时向低频移动，低频消声性能得到了提升。采用本文给出的弹性管壁参数条件，扩张式消声器的最大消声量从13 dB提高至18 dB，共振频率从600 Hz降低至350 Hz。

（2）随着弹性模量的降低，弹性壁扩张式消声器的传递损失曲线进一步地向低频移动；增大管壁材料的密度使弹性壁扩张式消声器传递损失曲线向低频方向移动，然而，对低频消声性能影响不大；阻尼系数的增加，弹性壁扩张式消声器在通过频率处的传递损失得到了提高，对于提高消声器宽频范围的消声性能有利。

（3）采用等效流体模型法近似求解弹性壁扩张式消声器的传递损失特性，在0～900 Hz 范围内能够取得满意的精度，同时简化了求解过程。