重力勘查工作中基于大样法的松散沉积层密度测定方法的改进

耿涛,冯凡,杜辉,冯治汉,郭培虹

(1.中国地质调查局 西安地质调查中心，陕西 西安 710054； 2.西北地质科技创新中心，陕西 西安710054； 3.西安西北有色物化探总队有限公司，陕西 西安 710068)

0 引言

重力勘查是以地壳中不同岩(矿)石之间的密度差异为基础，通过观测和研究天然重力场的变化规律，用以查明地下地质构造和寻找有用矿产资源及能源的地球物理勘查方法。随着技术的进步，重力勘查技术的精度越来越高，应用领域也越来越广，相应地，其对已知条件的精度要求也越来越高。

在重力勘查工作中，需要通过大量的工作去测定工作区内出露的各种地层和岩(矿)石密度来作为已知条件，为后续研究工作打好基础。松散沉积层的密度测定，是密度测定工作的重要组成部分，尤其是第四系覆盖区的重力勘查工作中，准确测定松散沉积层的密度，对重力资料的改正、处理、反演、解释研究等都具有非常重要的意义，各种地层、岩(矿)石密度值测定的准确与否，直接影响最终勘探结果的正确性及准确性。因此，密度测定的精度要求是很高的，规范要求密度测定均方误差要优于±0.02 g/cm3。

与致密岩(矿)石密度测量方法不同，松散沉积层由于开挖以后其结构就发生了变化，因此只能通过测量采样坑的体积来计算密度值，这也决定了松散沉积层的密度只能用大样法(large sample method)在原位测定,且不能通过重复测定来统计松散沉积层密度测定的误差。

在各种重力规范规程[1-5]中，并没有给出大样法的具体做法，只是规定按规则形体直接取出一定体积的松散沉积层样本，测定重量，利用式(1)计算其密度。

(1)

式中：P为大样的质量，V为大样的体积。

同时，规范建议：大样法测定松散沉积层密度时，取样体积应适中，一般以0.5 m×0.5 m×0.5 m为宜。

现在野外工作中均采用挖取长方体的大样法测量松散沉积层的密度。具体做法为：在采样点处，将表层疏松层剥离修平，然后挖一个大约为0.5 m×0.5 m×0.5 m见方的标准长方体(如图1所示)，边挖边将挖出的物质分别称重，待挖好后，测量长方体的长(L)、宽(W)、深(H)，用式(2)直接计算松散沉积层的密度。

(2)

式中：∑P为长方体中所有挖出物质质量之和。

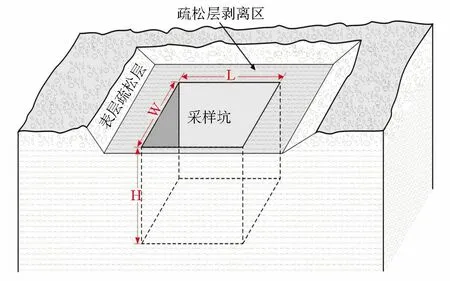
图1 一般大样法采样方法示意Fig.1 Schematic diagram of large sample method

上述的大样采样方法相当简便，在现场经过简单的计算就可得出结果，因此该方法是在重力野外工作中普遍采用的测定松散沉积层的密度的方法。

但是，这种方法存在明显的问题，即对采样坑的形状有严格的要求，必须是标准的长方体形状。然而，在野外工作中，这一点很难做到，尤其是西北较干旱地区，松散沉积层含水量少，含沙量较高，结构松散，因此，在挖大样的过程中，往往是边修整边垮塌，最后花费了很长时间，发现挖成的采样坑往往是一个近似长方体的不规则六面体，如图2所示。

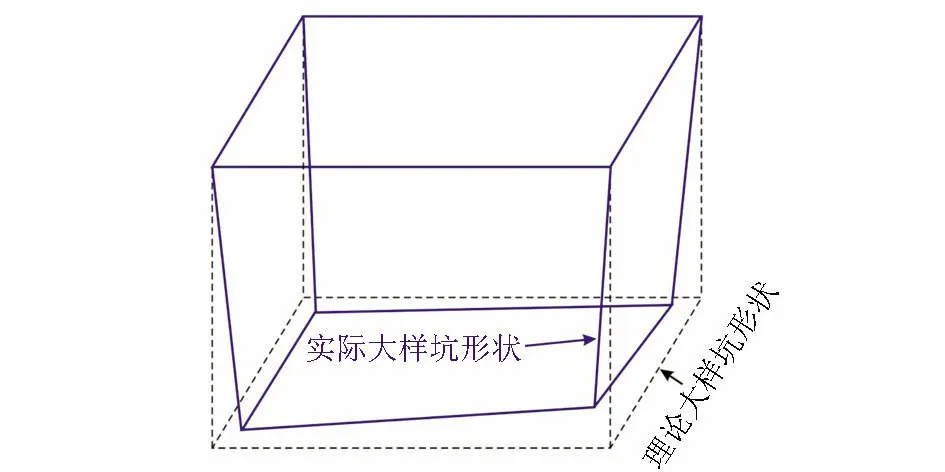
图2 实际采样坑与理论采样坑的差异示意Fig.2 Diagram of difference between actual sampling pit and theoretical sampling pit

这个不规则六面体一般都是上大下小，因此，利用开口处测量的长宽进行计算，计算出的体积(V计算)比实际挖出的不规则六面体采样坑体积(V实际)要大，导致最终计算出的松散沉积层密度较其实际密度偏小。

通过在西北地区大量的野外实际调查发现，即使非常认真仔细地修整，采样坑也难以达到标准长方体形态，用计算出的体积(V计算)与采样坑的实际体积(V实际)分别计算的密度值相比，发现其经常偏小0.1～0.2 g/cm3，有些情况下甚至更大，这对于一般介于1.6～2.2 g/cm3之间的松散沉积层密度值来说，相对误差一般大于7%～10%，甚至更大，这是不能忍受的。

需要说明的是，上述误差是在对该问题进行研究时，在非常认真的工作状态下得到的结果，而一般生产性野外重力勘查工作中，由于上述大样法非常简单，因此基本不把此项工作作为技术工作来做，而是作为简单体力劳动雇工完成，所以实际误差经常会更大，而且大样法具有不可重复测量的特点，缺少质量检查，往往是测成什么样就什么样。这也是在实际的松散沉积层密度测量资料中经常会见到一些密度值数据明显小于正常值范围，甚至出现极其不合理数据的一个重要原因。因此，如何基于大样法获取准确的松散沉积层的密度成为必须解决的问题。

笔者在以前的一篇文章[6]中曾简要提到用大样法测定松散沉积层密度存在的问题，并建议采用棱台体积计算公式替代长方体体积计算公式来计算采样坑的体积。但实际工作中发现采样坑大多都是不规则的近似六面体，并不符合棱台体的标准，用棱台体积计算公式计算的采样坑体积也是有误差的，因此，本文提出一种新的改进方法。

1 对常用大样法的改进

由以上分析可见，造成松散沉积层密度测定不准确的一个重要原因是所挖采样坑的体积计算不准确。如果能准确计算出采样坑的体积，那么，采样坑挖成什么形状其实并不重要，以前在野外工作中都尽量挖成长方体，只是为了体积计算方便而已。既然野外一般只能挖成近似长方体的不规则六面积，那么，只要能准确计算出这个不规则六面体的体积，就能解决这个问题。

不规则六面体体积的计算较为复杂，考虑到野外实际测量中，一般只能测长度，而不能测角度(测不准)，因此，我们按以下方法来计算不规则六面体的体积。

1.1 任意六面体转换为四面体

如果六面体的结点编号为i，六面体的表面编号为J(图3)，则结点i和不经过结点i的六面体表面J构成一个五面体体积为：

ViJ(i=1，2，…，8；J=1，2，…，6)。

图3 六面体角点、表面编号及特征参数的定义Fig.3 The numbering of the corner nodes and the surfaces of a hexahedral element,and the definition of the shape parameters

显然有关系式：

ViI+ViJ+ViK=V,

(3)

式中:V为六面体的体积；I、J、K分别为不经过结点i的3个表面编号。当结点i=1时，形成的3个五面体为：1-surf.2(1-2376)、1-surf.4(1-3487)、1-surf.6(1-5678)。

1个五面体又可以分割为2个四面体(图4)。

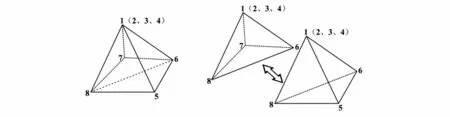
图4 六面体单元形状退化形式Fig.4 Degeneration forms of hexahedral elements

1.2 四面体的体积计算

分别计算分割出的各个四面体的体积。

首先求四面体1-567的体积。为方便表述，用O-ABC代表四面体1-567。建立如图5所示坐标系，以O点为原点，设A，B，C三点的坐标分别为(a1,b1,c1)、(a2,b2,c2)和(a3,b3,c3)，并设四面体O-ABC的6条棱长分别为BC=l，AB=n，AC=m，OA=p，OB=q，OC=r。需要说明的是，从棱锥的顶点向底面，底面角点逆时针编号)。

图5 用于计算四面体体积的坐标系Fig.5 Coordinate system used to calculate the volume of tetrahedron

由立体几何知道，该四面体的体积V等于以向量OA、OB、OC组成右手系时，以它们为棱的平行六面体的体积V6的1/6(图6)。

图6 平行六面体可分割为六个相等的四面体Fig.6 A parallelepiped can be divided into six equal tetrahedrons

于是得

将上式平方，得

根据向量的数量积的坐标表示，有

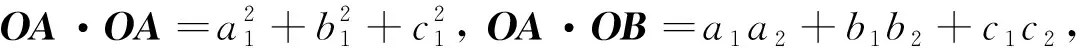
于是

(4)

由余弦定理，可得

同理

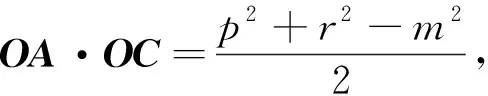
将以上各式代入式(4)，得

即可计算出四面体O-ABC的体积V：

其他5个四面体以此类推，最后，对6个四面体体积求和，即为六面体的体积。

1.3 野外工作中需测量的参数

为了达成上述计算不规则六面体采样坑体积的目的，野外实际工作中，需对以下22个参数进行测量(图7)。

图7 野外工作中需要测量的参数Fig.7 Need to measure parameters in field work

1) 采样坑的8条边长

需测量采样坑开口处的4条边S12、S23、S34、S14的长度及4条向下的边S15、S26、S37、S48的长度(图7a中的蓝线部分)。

2) 采样坑开口及侧壁的对角线长

需测量采样坑开口处的两条对角线S13、S24的长度及4个侧壁的8条对角线S16、S25、S27、S36、S38、S47、S45、S18的长度(图7b中的红线部分)。

3) 采样坑4条空间对角线长

需测量采样坑4条对角线S17、S28、S35、S46的长度(图7c中的绿线部分)。

4) 无需测量采样坑底部各边的长

在野外实际工作当中，测量采样坑底部4条边的长度相对比较困难，一是测量人员下坑测量较困难，且不易测准，二是容易弄塌采样坑边部，破坏其形状。针对这一问题，我们通过测定其他参数，采用以下的方法计算出底部各边的长度，避免去直接测量。

∠CAD=∠A-∠BAC。

根据三角形余弦定理，可得边长CD的长度为：

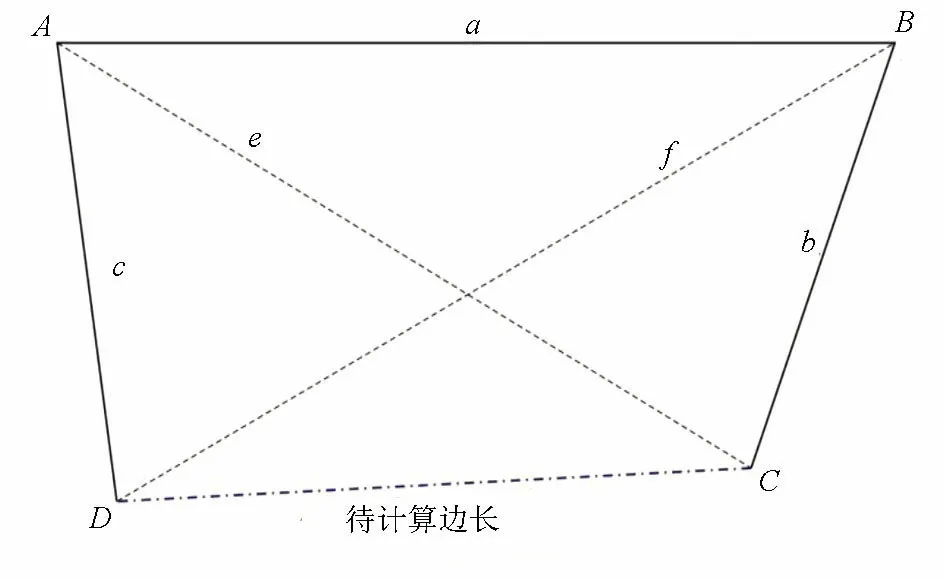
图8 不规则四边形已知条件及待计算边长Fig.8 The known conditions of irregular quadrilateral and the side length to be calculated

1.4 程序设计

显然，上述采样坑体积的计算，用简单的手工方法已不可能完成了，需要编程进行处理。

图9为我们依据上述计算公式开发的大样法密度计算程序界面。各测量边的数据输入过程中，示意图中有数据的边即变色。输入数据的单位：长度单位为厘米(cm)，样品重量单位为千克(kg)。

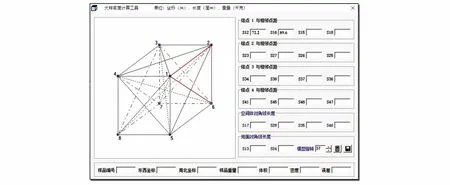
图9 大样密度计算程序界面Fig.9 Interface of calculation program for large sample density

完成所有数据输入后，可计算、保存数据。通过测量误差、示意图的图形形状可判断数据输入是否正确。

在上述计算过程中，采样坑开口处的对角线测量一条就可以了，另一条可通过以下方法计算出来。

已知任意四边形ABCD的边长AB=a，BC=b，CD=c，AD=d，对角线AC=e，那么，可通过下面的方法求出另一条对角线长BD的长度。

但是，为了防止里外测量出现混乱，程序中要求两条对角线的长度都要输入，这样，一来防止了野外出错，还可以通过计算出的结果与输入数据进行比对，判断野外数据测量误差，对数据测量质量进行初步控制。

2 本方法的优点

在野外采用大样法测定松散沉积层密度是一件比较费时费力的工作，而采样坑的形状不符合计算公式又是造成松散沉积层密度不准确的重要原因。为了减小误差，工作时都必须小心翼翼地修整采样坑。如果工作人员不用心或由于松散沉积层物质结构问题，边修边塌，根本修整不成一个较接近要求的形状，那么最终结果的误差就更大了。

本方法的优点在于，不必拘泥于采样坑的形状，只要是个六面体就行(而且这种形状较其他几何形态是最容易挖的)，采用本方法均可准确计算出其体积。因此挖掘时不必随时考虑采样坑形状，可以避开地层物质不均匀造成的坍塌等干扰，采样坑内各个面在修整时也不需有太多顾虑，只需修整成平面即可。

本方法野外测量的参数较常用方法有较大提高，但其所花费的时间和精力相较于小心翼翼地修整采样坑的形状，还是省时省力的。

3 野外工作中应注意的问题

与测定其他致密岩(矿)石密度不同，采用大样法测定松散沉积层的密度，在同一个采样点上是不可重复的，无法通过重复测量来确定其精度。因此，采样过程中的每一步工作都非常重要，都会影响到最终结果的准确性。

为了保证测量的准确性，在野外采样工作中，应注意以下问题：

1) 开始工作前，应充分研究工作区内松散沉积层的类型及分布、物质构成等，规划好采样点的大体位置，做到采样时心中有数。

2) 采样时，表层疏松层一定要剥离干净，至相对密实的压实层，修整平整，再开始挖样，表层的疏松层不代表实际的松散沉积层密度。疏松层剥离的范围要大一些，防止正式采样时周围的疏松层物质掉入采样坑内。

3) 在规划的采样点附近，如果有较新的陡坎、冲沟等，宜在其下部采样，最好是其下部侧壁上采样，可有效避免表层疏松层的影响。

4) 采样过程中，如果发现采样点过于干燥而坍塌严重，疏松层太厚难以剥离或板结太硬难以挖掘等，应果断放弃，在附近另寻采样点，不要强行采样凑数。

5) 疏松层剥离平整完成后，正式开始采样时，挖出的所有物质均应回收称重记录，不能遗漏。

6) 采样坑内五个面都应尽最大努力修整成平面，每条边修整成直线，以保证采样坑为一个六面体。

7) 因为采样坑内各个面间很难做到真正的直线相交，一般都是弧形的，因此，边长测量时应测至两边相交的位置(如图10)。

图10 边长的正确测量方法Fig.10 Correct method of measuring side length

8) 建议使用测量专用的金属折叠尺，采用两次测量取平均值的方法来得出每个参数的值。

9) 在可能的情况下，采样坑应尽量挖得大一些，这样可以降低由于测量不准确带来的误差。

4 实际应用情况

2011年起，笔者即对松散沉积层密度测定工作中存在的问题进行了研究，并提出了采用棱台体积计算公式替代长方体体积计算公式计算采样坑体积的解决方案[6]，但在后来的实际应用中发现，在西北一些地区，采样坑也难以挖成标准的棱台形状，于是，将采样坑体积计算方法进一步改进为本文所述的计算方法。

改进的方法目前已分别在陕西华阳川和甘肃金川两地的重力工作中进行了应用。从应用情况来看，首先，由于不用仔细地修整采样坑的形状，因此，挖掘采样坑的时间大为缩短，经对比(即先按改进方法挖好采样坑，测量后再按标准长方体采样坑要求修整)发现，改进的方法挖掘采样坑的时间约能节省1/2到2/3，尤其是在甘肃金川潮水盆地这种地表干燥疏松的戈壁地区，效果更为明显。其次，松散沉积层密度测定结果统计发现，测定数据的稳定性大大提高，相同成因及物质构成的松散沉积层测定的密度值不会出现大幅度的变化。这些都说明，改进的松散沉积层密度测定方法不仅提高了测定结果的可靠性，同时也大大节约了采样时间，减轻了野外工作强度。

5 结语

从密度测定的原理可知，只要知道样品的体积和质量，就可以求出样品的密度，因此，测定松散沉积层密度时，并未对采样坑的形状有任何限制，只要能精确测量出其体积和质量就行。但在实际野外工作中，是以方便易行为首要原则的，对于四面体(三棱锥)和五面体(四棱锥)这样的形状来说，不可避免地会有尖锐的顶角和锐角的棱出现，采用一般的挖掘工具很难挖掘，除非采用特种工具，这不太现实；而要挖掘顶面边数≥5的棱柱体形状的采样坑，不仅要增加工作量，也同样面临长方体采样坑面临的很难修整成标准形状的问题，因此，六面体采样坑是最易挖掘的形状。

本文提出的大样法测定松散沉积层密度的改进方法，并非是要取代规则形体的大样法，而是为重力勘查工作中的松散沉积层密度测定多提供一种工具。对于一些构成物质细密且粘性较大的松散沉积层，如果采样坑能挖成标准的长方体或上大下小的棱台体，则完全可以采用长方体或棱台体体积计算公式来计算采样坑的体积，而不必采用本文提供的较复杂的方法来计算。

当然，如果能有相应的专用设备来完成松散沉积层密度的采样测定工作，那是最理想的结果，或者是研制相应的软件，利用激光测距技术或三维全景扫描技术，配合掌上电脑，在野外快速测量任意形状采样坑的体积，在现今的技术条件下都是可行的，未来如果有大的需求，这些都不难实现。但在现阶段，松散沉积层密度的采样测定工作毕竟是一个重力调查工作中密度测定工作中的一小部分，需求很少，从成本效益方面考虑，可能没有单位愿意去开发相应的仪器设备。

然而，前文已经谈到，松散沉积层的密度测定又是密度测定工作的重要组成部分，对重力资料的改正、处理、反演、解释研究等都具有非常重要的意义。但是，松散沉积层的密度测定又有不可重复检查、缺少质量监控的特点，因此，在这项工作中，严谨、认真、科学的态度是非常重要的。试想，如果在采样过程中，不能准确测量采样坑的体积，不能完全回收并称量所有挖出物质的质量，那么，计算出的松散沉积层密度结果可想而知。因此，野外工作中，必须把松散沉积层的密度测定工作作为一项专业技术工作，严格按照要求来做，如果只是为了完成工作量，敷衍了事，那么，取得的数据就不能反映实际的情况，这项工作也就失去了意义。改进松散沉积层密度的采样测定方法的目的，也就是在现有的工作条件下，能较好地解决以前松散沉积层密度测定工作中存在的问题。