曲波变换在位场信号提取中的应用研究

张杨，王君恒，曹炼鹏，冯裕华，朱江皇，付强

(1.中国地质大学(北京) 地球物理与信息技术学院，北京 100083； 2.深圳市地质环境监测中心，广东 深圳 518034)

0 引言

重磁勘探技术是地球物理勘探中重要的方法之一。近年来，随着深部探测和航空重磁勘探技术的发展，对有效信号分离提取的需求越来越大。大区域产生的背景场中，经常包含微小的局部地质体产生的异常，因此，如何在密度差异或磁性差异不明显和存在强干扰的情况下，划分出不同地质体的边界、消除干扰的背景场、去除噪声的影响，己成为急需解决的问题[1-4]。

Curvelet变换是Candès和Donoho在1999年最先提出的方法[5]，为了让Curvelet变换更容易被人们理解和使用，Candès等先后提出第二代Curvelet变换框架体系，提出两种以第二代Curvelet变换理论为基础的快速离散实现方法。新算法理论的提出，使得Curvelet变换的实现更简单、快速，减少了初代算法带来的复杂冗余[6-9]。

在国内外，许多学者将Curvelet变换运用于各种数据处理，如图像数据、地震资料数据等[10-21]。国内学者将Curvelet变换运用于位场数据处理方面的研究较少，陈召曦通过建立简单、复杂组合模型对Curvelet变换的多尺度、多方向性进行了分析[22]。郇恒飞研究了Curvelet变换和小波阈值去噪方法在位场数据处理中的应用，通过模型试验对两种去噪方法的效果进行对比[23]。高铁等进行了 Curvelet 变换去噪和小波阈值去噪的实验对比，验证了 Curvelet 变换去噪的有效性[24]。杨斯涵研究Curvelet变换的多尺度分析性质及其去噪原理，得出Curvelet多尺度分解后各层系数重构数据可以与地下不同深度规模异常体相对应的结论[25]。

笔者首先介绍了Curvelet变换的基本原理，然后在前人研究的基础上开发了相关Curvelet变换软件，并且同时利用重力位场理论模型、加噪模型和南岭东部地区实际资料分析了Curvelet变换的分解和去噪能力。综合前人的研究成果，结果表明该方法可同时适用于位场数据的多尺度分解和去噪处理研究，为实际重磁数据的多尺度分析处理提供参考。

1 第二代Curvelet变换

第二代曲波变换是在小波变换、脊波变换和第一代曲波变换的基础上构建出来的。

二维空间R2中，x为空间的位置变量，ω为频率域变量，r、θ为对应频率域下的极坐标。假设存在平滑、实值非负的“角度窗”V(t)(支撑域为t∈[-1,1])和“半径窗”W(r)(支撑域区间为r∈(1/2,2))，且满足容许性条件:

(1)

对于每一个尺度j≥j0可以引入频率窗口Uj，定义频率域窗函数为：

(2)

式中：[j/2]表示j/2整数部分；频率域窗函数Uj为极坐标下受“半径窗”W和“角度窗”V支撑区间限定的楔形区域。

如果φj(x)的傅立叶变换满足等式

(3)

则定义φj(x)为母曲波函数。所以，在尺度2-j上所有的曲波函数都可以由φj(x)经过旋转与平移得到。

(4)

所以任何一个函数f∈L2(R2)的曲波变换系数c(j,l,k)可以通过此函数f与某一尺度上的曲波函数φj,l,k的内积来表示：

(5)

将地球物理数据应用于曲波变换时，地球物理数据可看作函数f，如本文使用的重力位场数据；将重力位场数据函数f与曲波函数φj,l,k进行内积c(j,l,k)=〈f,φj,l,k〉，就可以得到不同尺度下的曲波系数c(j,l,k)；对得到的曲波系数c(j,l,k)进行处理并反曲波变换重构，就可得到处理后的重力位场数据函数f′。

2 Curvelet变换应用

2.1 位场数据模型分离重构试验

二维数据函数f经过Curvelet多尺度变换分解后，在不同方向和不同分解尺度上都有对应的一组系数：

(6)

式中：Cj,0(k1,k2)为分解后原结果的低频系数，相当于数据的粗尺度部分，在该频带上无方向性；Cj,l(k1,k2)为尺度j，方向l下的高频系数，相当于数据的精细尺度部分。按照需要对不同尺度的系数进行处理，以达到实现数据的融合、去噪、多尺度、多方向等处理的要求，然后对处理后的系数进行选择性的反Curvelet变换重构，就可以得到处理后的结果。对于512×512的二维数据，经过Curvelet变换后，可以得到Curvelet系数如表1所示。

表1 512×512数据的Curvelet系数结构

随着层数的增加，反Curvelet变换重构的图像越精细，反映的越是高频成分和数据的细节部分，层数越低，反映的越是粗糙成分和低频成分。使用Curvelet变换就是把原始数据按照数据的大小多尺度分解为不同的层数，默认的层数大小设置为 ceil(log2min(M,N)-3)。对于512×512的二维数据，Curvelet变换分解为6层系数。

将Curvelet变换应用到重力数据，设置了5个场源体(直立六面体)和观测面组成的理论模型，观测面为z=0 km的平面，观测面z坐标方向向下为正。5个直立六面体场源分别编号为A1、A2、A3、B1和B2，其几何参数及密度参数见表2所示。将B1、B2看作深部区域异常，A1、A2、A3看作浅部局部异常，进行信号的分离提取。重力异常见图1。

表2 直立六面体场源参数统计

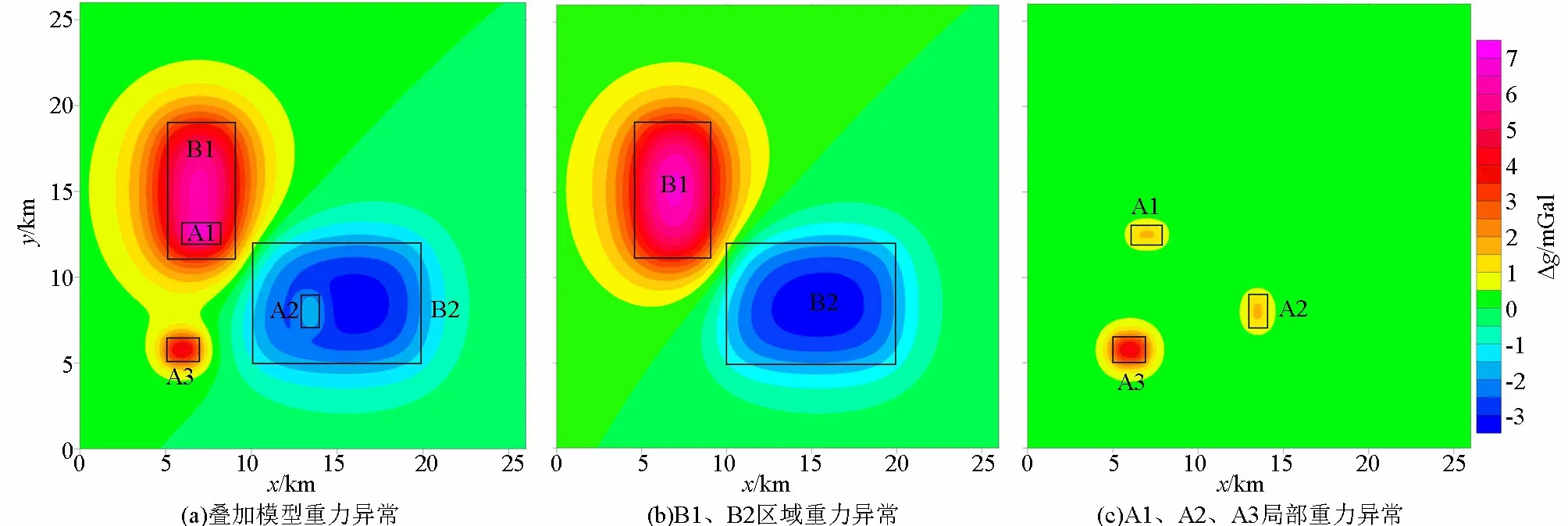
图1 直立六面体组合重力异常Fig.1 Vertical hexahedron combined gravity anomaly

对图1a重力数据进行Curvelet变换，分别提取6层的系数进行反Curvelet变换重构， Curvelet变换的多尺度分解性质能够完成位场数据的多尺度分解，可以对不同规模地质体所产生的不同尺度的重力异常进行分离，来达到重力位场多尺度分解的目的。规模大且埋藏深的地质体，重力异常通常表现为平缓的区域异常，经 Curvelet变换后得到低层系数；规模小、埋藏浅的地质体重力异常通常表现为变化剧烈的局部异常，经 Curvelet变换后得到高层系数(图2)。

图2 Curvelet变换分解后的系数重构重力异常Fig.2 Reconstructed graph of gravity anomaly with coefficients decomposed by Curvelet transform

第5层和第6层系数反映Curvelet变换重构图像数据近似为0，不能反映数据信息。将第1层图象定义为分解后得到的深层重力异常，重力平面图反映了埋深最深、规模最大的两个模型B1、B2的异常，消除了A1、A2模型的影响，但包含A3模型的影响，因为A3模型产生的重力异常幅值大，其重力异常在深层与浅层都有所体现。将第2层到第4层Curvelet系数重构图定义为浅层重力异常，包含埋深最浅、规模最小A1、A2、A3模型的异常。与图1对比，可以看到Curvelet系数第1层重构图体现了区域重力异常，反映深部数据，Curvelet系数第2层到第4层重构图体现了局部重力异常，反映浅部数据。

将A3模型的z坐标z1=0.5 km、z2=1.0 km改为z1=1.0 km、z2=1.4 km，原始叠加模型重力异常Curvelet变换重构图像见图3。

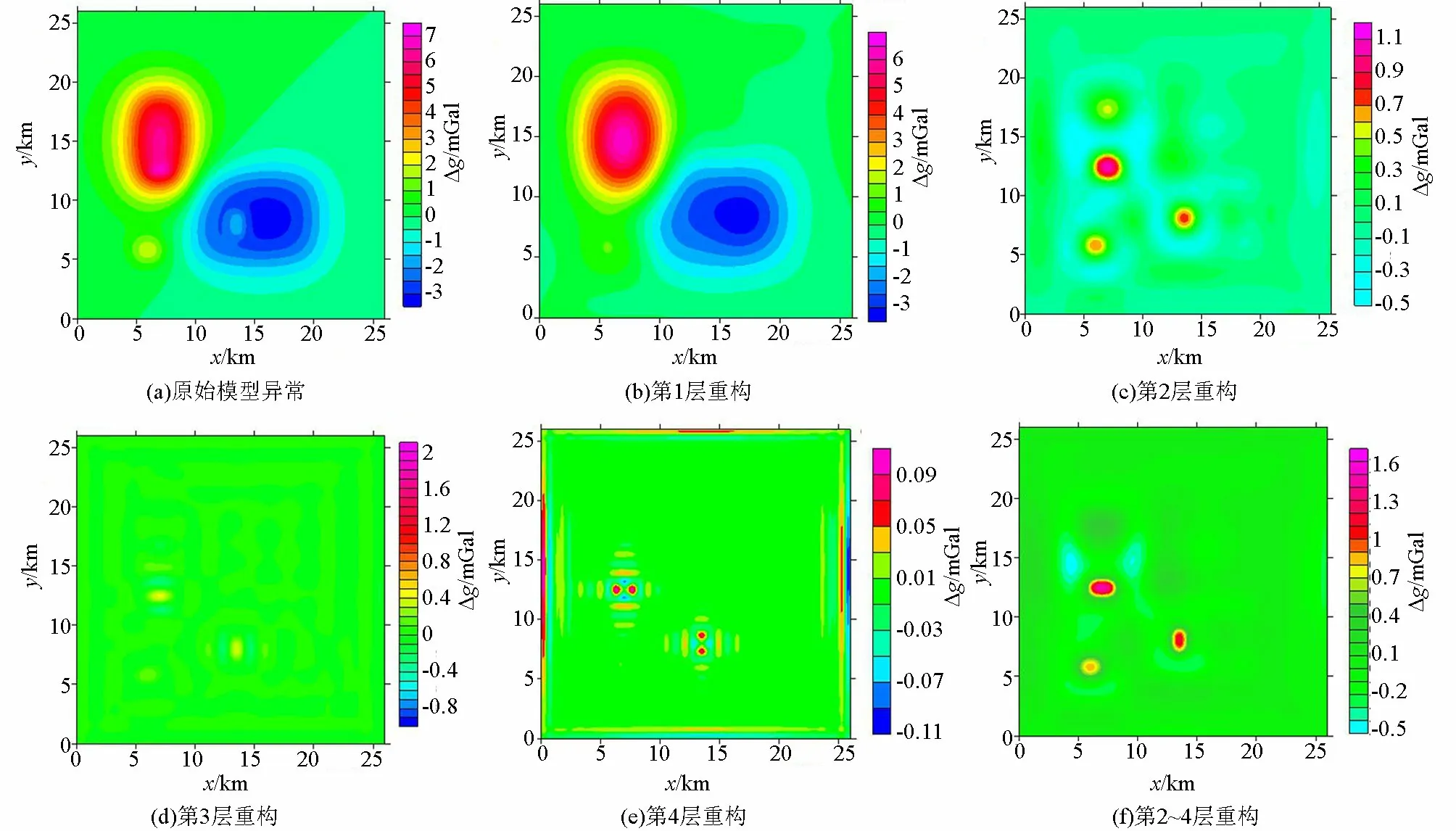
图3 Curvelet变换分解后的重构重力异常Fig.3 The reconstructed gravity anomaly map after the decomposition of the Curvelet transform

第5层和第6层系数重构图像近似为0，不能反映数据信息。将第1层图象定义为Curvelet分解后得到的深层重力异常，重力平面图反映了埋深最深、规模最大的两个模型B1、B2的重力异常，A3模型的重力异常影响被削弱，消除了A2、A1模型的影响，反映的是区域异常。将第2层系数重构图定义为中层重力异常，去掉了B1、B2模型体的重力异常，包含A1、A2、A3模型体产生的重力异常。将第3、4层系数重构结果定义为浅层重力异常，包含埋深最浅、规模最小A1、A2模型体的重力异常，去掉了A3模型体的影响。从分离结果来看，Curvelet变换有效地将不同深度层上的重力数据进行了分离，从而完成了位场数据的分解。

图3与图2对比，A3模型可以看成中层重力模型，较B1、B2模型埋深浅，较A2、A1模型埋深深，故图3第1层重构图与图2第1层重构图相比，A3模型影响减弱；图3第3层和第4层重构图与图2第3层和第4层重构图相比，主要反映了A1、A2模型重力异常，A3模型重力异常被消除。所以，通过建立不同埋深的异常体，验证了该方法的分层效果。该方法分层结果与异常体大小、埋深和密度有关，分解的系数层数越高，反映的越是浅层异常或局部异常；系数层数越低，反映的越是深层异常或区域异常。

2.2 阈值去噪模型试验

Curvelet变换去噪的原理是，数据经过Curvelet变换之后，噪声通常在变换后会表现为绝对值很小的系数，所以，我们可以引入阈值分割的理念，对分解后每一层系数进行阈值分割，将数值较小的系数设置为0，对数值较大的系数则进行保留。实际数据中的有效信息通常在Curvelet变换后表现为数值较大的系数。因此，通过这种阈值判断，可以保留原始数据中的重要信息，进而消除噪声的干扰，再将处理后的系数进行反Curvelet变换重构，就达到了去噪的目的。此外，由于曲波变换实现了不同尺度、层次数据的分解，对分解后各层系数进行分析，可以发现，噪声通常集中在最高几层系数中，有时可以直接将具有严重噪声的系数层去掉，便可实现噪声滤除。

阈值去噪方法包含硬阈值、软阈值、自适应阈值等。此外，还可以根据不同情况对Curvelet变换系数进行处理来达到滤波的目的。

本文采用硬阈值去噪方法来处理位场数据资料，硬阈值去噪处理的方法原理是将大于设定阈值的系数保留，而小于阈值的系数设置为零。

(7)

式中：Cp为原始数据的Curvelet变换系数；Tm是设

对原始数据进行去噪可以分为3个步骤:

1) 对原始加噪数据进行Curvelet变换多尺度分解;

2) 对Curvelet变换分层系数采用硬阈值法，对每层系数进行处理;

3) 将处理过后的Curvelet变换系数进行反Curvelet变换，就可以得到经过阈值处理后的数据重构图。

将表2中重力位场数据加5%重力幅值的随机噪声进行Curvelet变换处理(图4)，可以看出噪声集中在4、5层，即高层系数重构数据中，第3层中也有少部分噪声干扰。

图4 加噪数据曲波变换重构Fig.4 The reconstructed image with noise-added data using Curvelet transform

去噪是通过对Curvelet系数进行硬阈值处理来实现的，最精细的尺度层被设置为4×sigma_jl阈值，其他层数选择3×sigma_jl的阈值，这里 sigma_jl是规模为j和角度l的系数的噪声水平(等于噪声水平乘以相应曲波系数的L2范数)。

对原始重力异常数据加噪声，然后应用Curvelet变换阈值去噪(见图5～7)，由以上模型的去噪实验可以看出，Curvelet变换阈值去噪方法效果良好，可以去掉不同幅值噪声的影响。

图5 加噪数据Curvelet变换阈值去噪(加10%幅值随机噪声,sigma=0.8)Fig.5 Curvelet transform threshold denoising of noise-added data(add 10% amplitude random noise，sigma=0.8)

图6 加噪数据Curvelet变换阈值去噪(加5%幅值随机噪声,sigma=0.45)Fig.6 Curvelet transform threshold denoising of noise-added data(add 5% amplitude random noise，sigma=0.45)

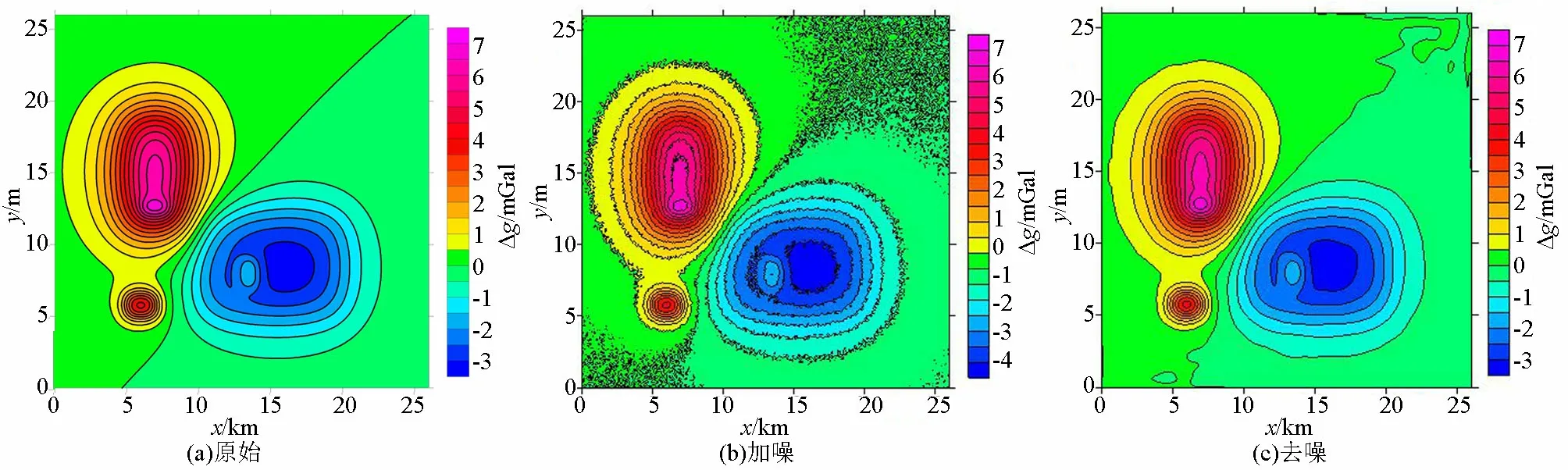
图7 加噪数据Curvelet变换阈值去噪(加1%幅值随机噪声,sigma=0.15)Fig.7 Curvelet transform threshold denoising of noise-added data(add 1% amplitude random noise，sigma=0.15)

2.3 实际资料处理

南岭位于华南地区的中南部，广泛发育不同成因、时代的花岗岩，盛产与花岗岩有密切成因关系的钨、锡稀有金属矿产，其成矿条件独特，而且成矿潜力巨大，专家学者对该区域的研究历史十分悠久[26-30]。

本次处理的重力位场实际资料是南岭东部区域EGM2008布格重力异常，数据范围：经度114°～116°，纬度24°30′～ 26°，网格化成大概1′× 1′的间距(见图8)。研究区地形见图9。

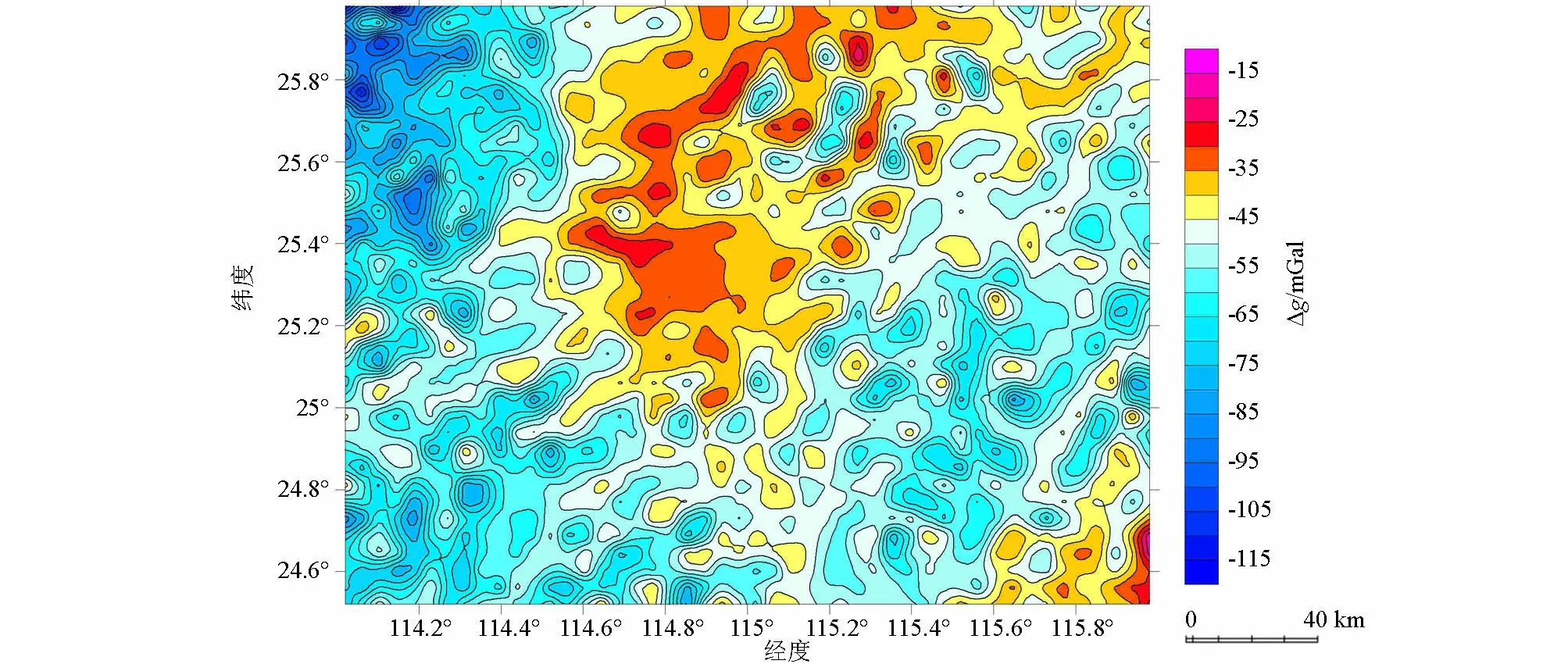
图8 南岭东部EGM2008布格重力异常Fig.8 Bouguer gravity anomaly map of EGM2008 in the eastern part of Nanling

图9 研究区地形Fig.9 Topographic map of the study area

南岭东部EGM2008布格重力异常是该区域地质体信息的综合反映，包括了壳内各种偏离正常密度分布的矿体与构造的影响，也包括了地壳下界面起伏的影响等。从原始资料(图8)可以看出，中部区域以及东南角区域布格重力异常值高，对应地形图中地形高程相对较低，西北角区域布格重力异常值最低，对应地形图中地形高程相对较高，布格重力异常范围为-115～-15 mGal，布格重力异常能与地形图高程信息联系起来。

对南岭东部EGM2008布格重力异常数据进行Curvelet变换处理，分解为4层Curvelet系数，将第1层曲波系数设为深部层，第2层曲波系数设为中部层，第3层曲波系数设为浅部层，第4层曲波系数设为噪声干扰层，对深部层、中部层、浅部层和干扰层曲波系数进行反Curvelet变换重构，就可以得到深层、中层、浅层和噪声干扰层重力异常平面(图10)。

图10 Curvelet变换重构重力异常Fig.10 The reconstructed gravity anomaly map using Curvelet transform

综合前人研究成果，如参考罗凡华南地区卫星布格重力异常和华南地区仅反映莫霍面变化的卫星布格重力异常[31]，结合图10a可以认为第1层Curvelet系数重构重力异常图近似为深部区域异常，消除了大部分局部异常的干扰。大体上中部区域和东南角区域重力异常高，对应该区域地形高程值相对较小，西北角区域重力异常值低，对应该区域地形高程值相对较大，能与地形图高程信息联系起来。重力异常范围为-95～-32 mGal，红色为重力异常高值，蓝色为重力异常低值。

对于图10b中，第2层系数重构重力异常图近似为中层深度局部异常体或构造产生的重力异常。图10c中，第3层系数重构重力异常图近似为浅层局部异常体或各种地质构造产生的重力异常。图10d为高频干扰异常。

将图10c中第3层系数重构重力异常图与该区域地质图(图11)进行对比，对比图见图12，可以看到地质图中标定的钨矿与锡矿的岩体分布(深蓝色和棕色圆圈)与图10c中重力异常体的分布和走向大致相似，可以认为图10c主要反映了浅层密度不均匀矿体、花岗岩岩体边界及各种地质构造等产生的局部重力异常，对浅地表矿体分布或地质构造等信息具有一定指示作用。

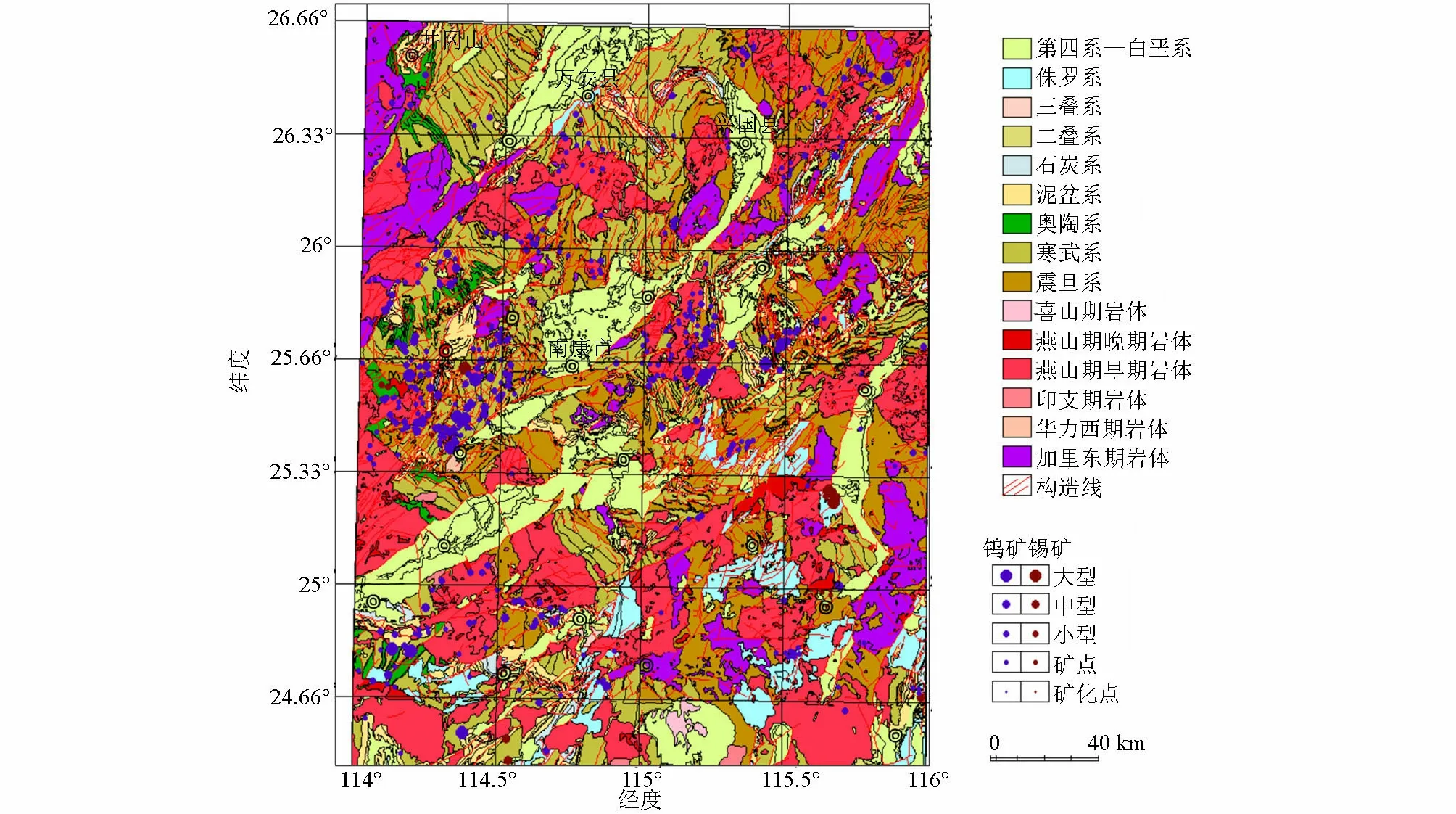
图11 南岭东部地质简图Fig.11 Geological sketch map of eastern Nanling

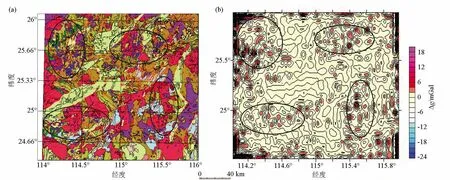
图12 南岭东部地质简图(a)与重力异常(b)对比Fig.12 Comparison of geological sketch map (a) and gravity anomaly map (b) of eastern Nanling

3 结论

1) Curvelet变换根据原始数据的大小将其分解为不同尺度的系数，各个尺度的系数又可以经过处理后反Curvelet变换为重构数据，并且各个尺度的系数相互之间可以叠加、增删。

2) Curvelet变换阈值去噪中，噪声信号为高频细节信号，一般在分解重构的高层系数中，对高层系数进行阈值处理可以有效去掉噪声的干扰。

3) Curvelet变换运用于位场数据中，可以近似的认为，低层系数重构数据表示深层区域异常信号，中层系数重构数据表示中层异常体产生的信号， 高层系数重构图表示浅层局部异常体信号。由南岭实测数据处理看出，低层Curvelet系数重构重力异常可以近似认为深部区域重力异常，高层Curvelet系数重构重力异常可以近似认为浅层密度不均匀矿体、花岗岩岩体边界及各种地质构造等产生的局部重力异常，对浅地表地质体或各种地质构造信息具有一定指示作用。

致谢：感谢审稿人和编辑对本文提出的宝贵意见。感谢中国地质大学(北京)同学和深圳市地质环境监测中心的帮助。