一类Copulas最优界的扰动及其相关性和对称性

李丽君，徐付霞

(天津工业大学 数学科学学院，天津 300387)

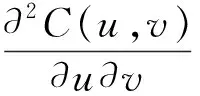
(1)

则C(u,v)=AC(u,v)+SC(u,v). 若SC为0，则称C是绝对连续的，如乘积CopulaΠ=uv和FGM CopulaCθ(u,v)=uv+θuv(1-u)(1-v)等是绝对连续的. 若AC为0, 则称C是奇异的, 如Frechet-Hoeffding上下界M(u,v)=min(u,v)和W(u,v)=max(u+v-1,0), 以及单点值给定的Copula最优上下界CU,CL:

CU(u,v)=min(u,v,θ+(u-a)++(v-b)+)

(2)

CL(u,v)=max(0,u+v-1,θ-(a-u)+-(b-v)+)

(3)

是奇异的[2]. Mesiar[3]研究了如下形式的扰动Copula

(4)

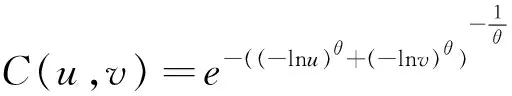
(5)

(6)

(7)

(8)

董永权[6]给出最大不可交换Copula的Spearman′sρ和Kendall′sτ秩相关系数的取值范围, 以及两种秩相关系数与 Blomqvist′sβ中位相关系数的关系. 徐付霞[7]研究了连续型广义FGM Copulas 的相关性度量, 说明ρ,τ,γ和β相比于线性相关系数的优越性. 徐付霞[8]基于Copula理论的随机变量的相关性, 研究了某个单点值给定时Copula 最优上下界的其他相关性度量φU,φL.本文旨在研究奇异型Copula增加扰动项后的新型Copula, 扰动参数对新型Copula 四种和谐性度量的影响.以Frechet-Hoeffding上下界M和W,CU和CL为例进行深入分析. 计算其和谐性度量和不可交换性度量, 得到扰动参数对和谐性度量和对称性的影响, 揭示增加扰动项后的奇异Copula的结构特点和性质.

目前, 国内外用Copula构造相关性度量研究的文献[9-11]很多, 但大多基于连续型的Copula, 如FGM Copulas, Archimedean Copulas, Clayton Copulas进行构造及相关性分析, 对奇异型Copula 研究较少. 本文对奇异型Copula增加扰动项构造新的Copula, 并对其相关性度量进行分析. 首先研究Frechet-Hoeffding 上下界添加扰动项构造新的Copula的和谐性度量. 进一步, 研究单点值给定的Copula的最佳上下界CU和CL增加扰动项后构造的新的Copula的和谐性度量和不可交换性度量.

1 基于M和W的扰动Copula相关性度量

令C(u,v)=M(u,v)=min(u,v)由公式(4)给出的扰动Copula

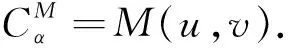
定理1 令C(u,v)=W(u,v)=max(u+v-1,0)，由式(4)给出的扰动Copula

(9)

的四个和谐性度量分别为:

证明：由式(5) 得到

由式(6)

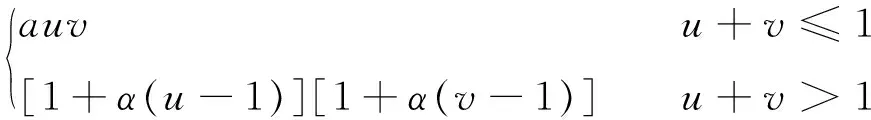
所以

由式(7)，

由式(8)

综上，Copula增加扰动项后原Copula的相关系数-1由数拓展为区间[-1,1]，增加了Copula 的适用性.

2 基于CU的扰动Copula相关性度量

如果已知Copula的某些信息, 比如某个点的值已知, 它的Frechet-Hoeffding上下界会变窄:

定理2 设C是一个Copula, 若存在点(a,b)∈I2及θ满足max(a+b-1)≤θ≤min(a,b)使得C(a,b)=θ，那么对任意的(u,v)∈I2，都有

CL(u,v)≤C(u,v)≤CU(v,u)

其中：CU和CL由式(2)、(3)给出，它们是C(u,v)的最佳上下界.

对它增加扰动项：

(10)

研究单点值给定的最优界的扰动Copula的相关性度量的变化.

定理3 令C(u,v)=CU(u,v)=min(u,v,θ+(u-a)++(v-b)+)，则由公式(4)给出的扰动Copula的四个相关性度量分别是：

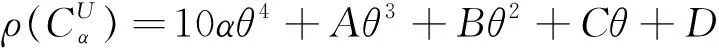
其中A=12-20α(a+b),B=12α(a2+3ab+b2)-18(a+b),C=-2α(a3+b3)-18αab(a+b)-6(a2+4ab+b2),D=2αab(a2+3ab+b2)-6ab(a+b)+1,E=4(α2ab-1)+2α2(a+b)2,F=4(a+b)-2α2ab(2a+b),G=1+2α2ab2(a-1)-4ab,H=-2αa-13αb-6α-7,I=a(2-α)+1/2(b-1)(3-α)-αb(2a+b),J=1/4b2(7-5α)+5b(1/2+1/3αb2)+αa(a-1)+ab(α-1)+1/4(α+1)+αb(2ab-1/2)

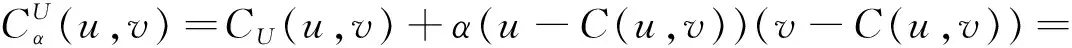
其中A1=[0,θ]×[0,u]∪[θ,a]×[u-θ+b,1]∪[a,a+b-θ]×[a+b-θ,1]∪[a+b-θ,1]×[u,1],B1=[0,θ]×[0,u]∪[a,θ]×[0,θ]∪[a,a+b-θ]×[0,u+θ-a]∪[a+b-θ,1]×[0,u],C1=[θ,a]×[θ,b],D1=[a,a+b-θ]×[a+θ-u,b],E1=[a,a+b-θ]×[u-a+θ,b],F1=[θ,a]×[b,u+b-θ],

其中，

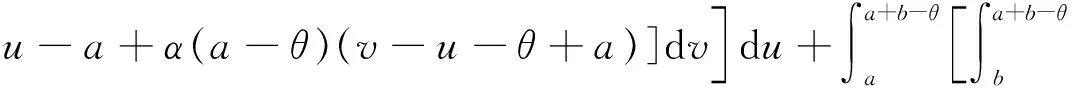
A,B,C,D的表达式见定理3.

由式(6)

得到

Eθ3+Fθ2+Gθ+H

其中:E,F,G,H的表达式见定理3.

由式(7)，得到

其中：I,J,K的表达式见定理3.

当(u,v)=(1/2,1/2)时，b-θ≤a-b≤a-θ时，落入[θ,a]×[b,a+b-θ]区域内，得到

经验证，当α=0时所得的相关系数与文献[6]中结果一致，

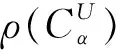
3 基于两类CU和CL的扰动Copula的不可交换性度量

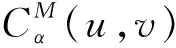
(11)

利用上式推导下面四个最大不可交换Copula：

(12)

(13)

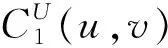
1) 当(u,v)落在v=u+1/3和v=u+2/3之间时, 有

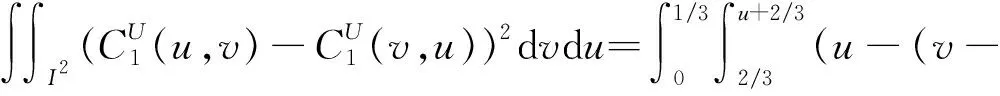
2) 当(u,v)落在v=u+1/3和v=u-1/3之间时, 有

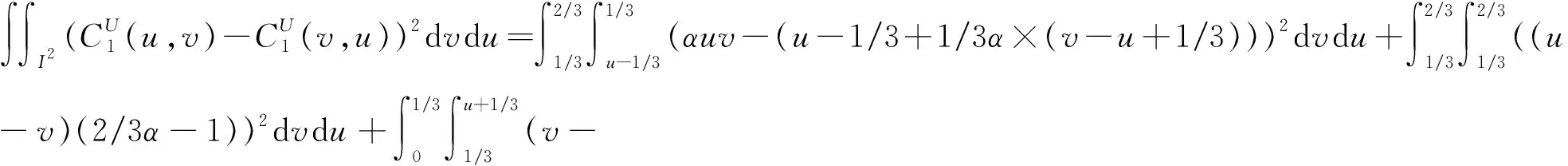
3) 当(u,v)落在v=u-1/3和v=u-2/3之间时, 有

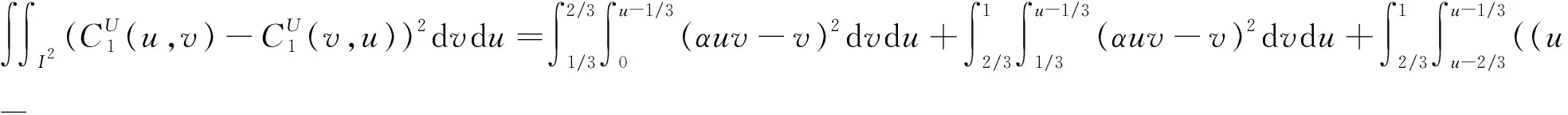
4 结 语

Copula函数最重要的功能就是度量随机变量之间的相关性. 奇异型Copula虽少，却是Copula函数不可缺少的组成部分，例如本文中研究的W，M，CU，CL是具有代表性的函数. 构造奇异型Copula族并研究其相关性度量和不可交换性度量，是基于Copula函数的理论研究，增加了Copula可描述的随机变量的范围，增加了它的适用性.