基于鲁棒性提高的航班计划优化模型

高 谦，王世瑞，高 强

（南京航空航天大学民航学院，江苏 南京211106）

2004 年Rosenberger[1]为了减少航班链上的延误和波及延误，通过采取了减少航班链长度和降低枢纽机场连通性的方法建立了鲁棒性优化模型，并且成功增加了航班计划的鲁棒性且减少了运营成本。Claudine[2]以增加非枢纽机场航班计划鲁棒性为目标，通过区别非枢纽机场的种类，建立了机组排班和机型指派的鲁棒性优化模型，并且成功增加了非枢纽机场航班计划的鲁棒性。Lan 等[3]提出了站在航空公司和旅客角度两种新的方法提高航班计划鲁棒性，分别以减少航班链长度和最小化延误影响的旅客数量为目标建立模型，两种方法都不同程度的减少了延误带来的成本增加。 Dunbar M[4]为了减少延误的总时间和延误总成本，提出了一种合并了飞机路线和机组规划鲁棒性的增强模型，并且有效的减少了延误成本。 Lee L H[5]为了解决鲁棒性求解问题，采用了多目标遗传算法对其通过仿真建立的多目标航班计划的鲁棒性优化模型进行求解，这种方法的优势在于可以在多重标准的情况下都可以求出最优解， 但这个最优解并不完全符合实际意义。 目前，国内学者朱新辉[6]提出了基于飞机排班的一体化鲁棒优化模型，通过设置双目标分别量化了整体航班计划的鲁棒性和运营成本，但是其模型并未考虑航班更改而产生的成本。 针对现有模型的不足，在这些模型的基础上建立基于鲁棒性提高的航班计划优化模型。

1 鲁棒性及运营成本计算

1.1 鲁棒性的定义及计算

鲁棒性（Robustness）是指当系统处于外界干扰时可以保持原系统状态的不变的能力和当系统状态改变时可以快速恢复系统状态的能力的综合能力。 针对航班计划来说，如果在制订航班计划时考虑到抵御航班延误和在已产生延误的基础上恢复航班状态，这就是提高航班计划的鲁棒性。 目前提高航班计划的鲁棒性的方法主要有：增加过站松弛时间、提高机型纯度、减少航班链长度。 由于提高机型纯度这种方法相对于航空公司来说短期实行成本巨大，故仅针对增加过站松弛时间和减少航班链来设计模型。 鲁棒性直接挂钩的变量为航班的起飞延误和到达延误， 故可以将鲁棒性的计算公式（1）进行定义[7]

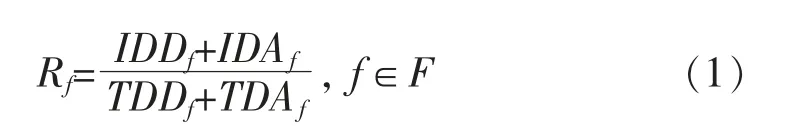
式中：Rf表示某个航班f 的鲁棒性；IDDf代表航班f的固有起飞延误；IDAf代表航班f 的固有到达延误；TDDf代表航班f 的实际起飞延误；TDAf代表航班f的实际到达延误；F 代表航班集合。 具体含义如图1所示[7]。

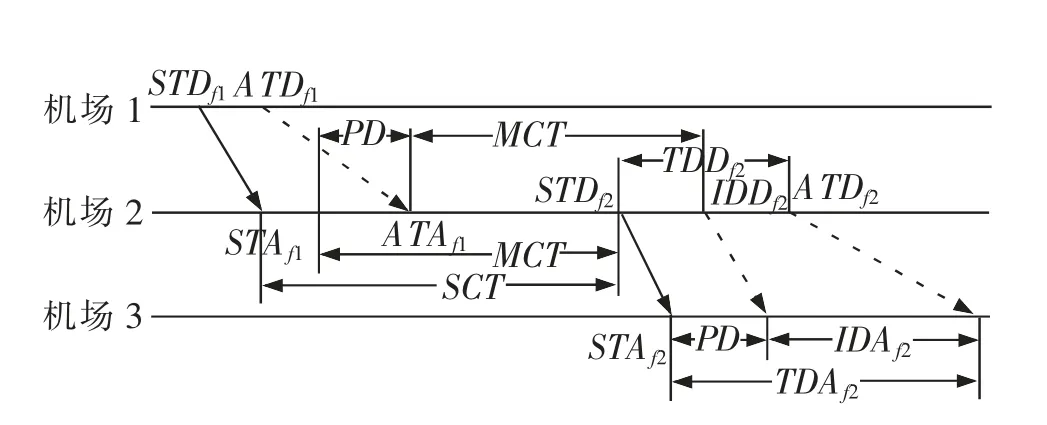
图1 航班延误示意图Fig.1 Schematic diagram of flight delays

图1 中STD 为计划起飞时间；SCT 为计划过站时间；TDD 为实际起飞延误；STA 为计划到达时间；MCT 为最小过站时间；TDA 为实际到达延误；ATD为实际起飞时间；IDD 为固有起飞延误；ATA 为实际到达时间；PD 为波及延误；IDA 为固有到达延误。

由于不考虑波及延误，故可将鲁棒性定义公式改为

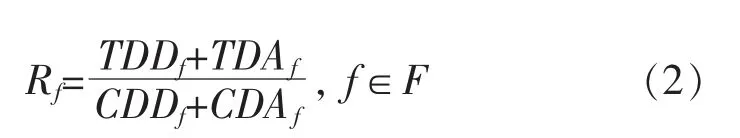
式中：CDDf代表航班f 的更改起飞延误；CDAf代表航班f 的更改到达延误。 具体含义如图2 所示。

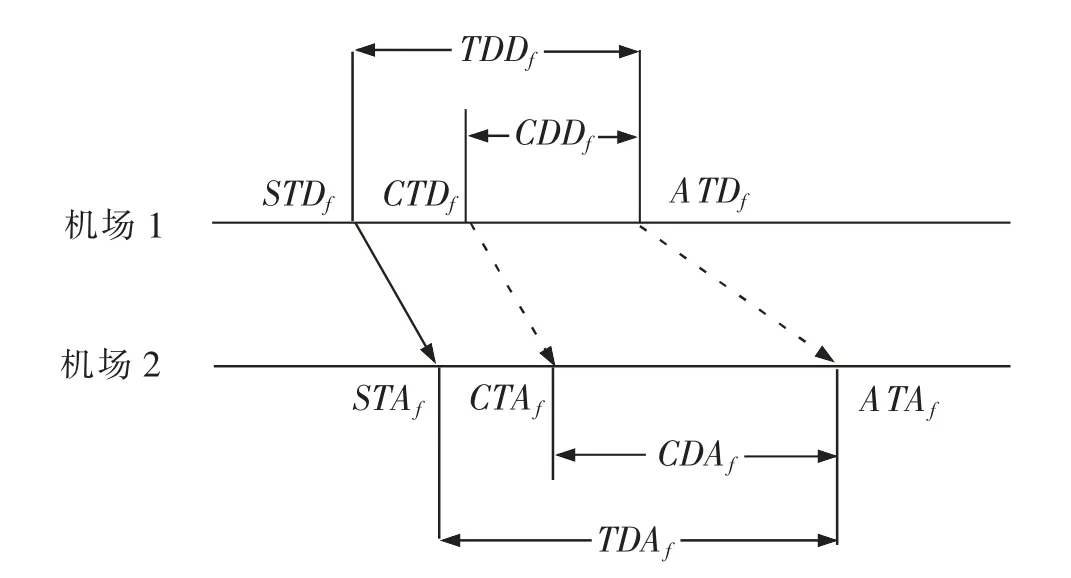
图2 更改航班计划示意图Fig.2 Sketch map of changing flight schedule

更改起飞延误为当更改起飞延误和更改到达延误的总和小于实际起飞延误和实际到达延误的总和时，总延误减少，Rf的值为正，航班f 鲁棒性增加；反之，总延误增加，Rf为负，航班f 鲁棒性减少。

1.2 航班计划运营成本的计算

航班计划运营成本分为计划运行成本和航班恢复成本两个部分。 计划运行成本为航班运行时所产生的固有成本，包括燃油成本、机组成本、折旧成本、维修成本、起降成本和航路成本等。

不同的机型每小时消耗的燃油体积不等，通过查阅资料得知目标航司的机型为波音737-800、波音737-300 和ERJ-145 的耗油量分别为2 650，2 800，1 200 L/h， 并且设置当下航空燃油成本为6元/L，就可以得出所有航班的燃油成本，计算公式如

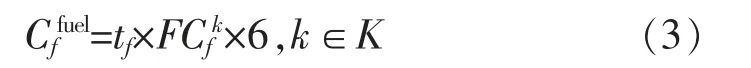
机组成本通过查阅相关资料可知该公司目标机型波音737-800、波音737-300 和ERJ-145 的机组人员数量分别为6，6，5 人。 根据机组人员每小时的工资可知，波音737-800 和波音737-300 每小时机组花费730 元，ERJ-145 每小时机组花费670元。 机组成本计算公式如

式中：Pairplane为购买飞机价格；Yyear为折旧年限Pengine为单台发动机价格；Rj为机型j 的残值率，一般按飞机售价的5%计算；U 为年轮挡小时数。

通过查阅相关资料可知该公司目标机型波音737-800， 波音737-300 和ERJ-145 的每小时的折旧成本分别为11 083，10 298，3 314 元。

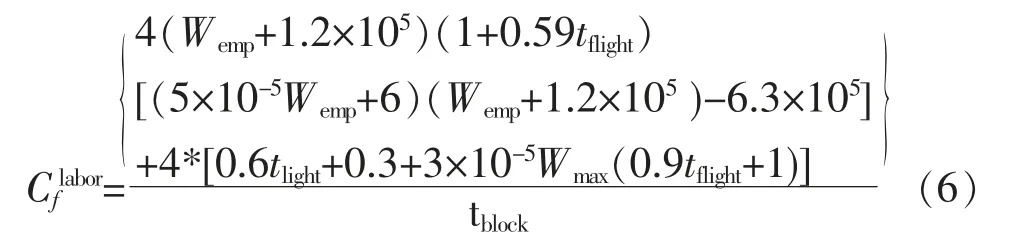
式中：Wemp为飞机空重；tflight为飞机飞行小时数；Wmax为最大起飞重量。

通过查阅相关资料可知该公司目标机型波音737-800， 波音737-300 和ERJ-145 的每小时维修成本为3 180，3 360，1 440 元。

其余的成本包括飞机起降成本和航路成本。 通过查阅相关资料可知该公司目标机型波音737-800， 波音737-300 和ERJ-145 的每架次起降成本为3 360，2 200，2 000 元； 每 公 里 航 路 成 本 为0.39，0.23，0.11 元。

由以上推算可知航班计划运营成本为如式（7）所示。 其中定值a 为航班起降成本与航路成本的和，具体到每一个航班来说为定值。

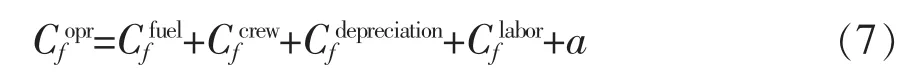
1.3 航班恢复成本的计算

航班计划恢复成本由延误成本， 取消成本，换机成本和调机成本组成[7]，由于换机和调机的成本过高，发生条件比较苛刻，故发生概率较低，暂不对换机成本和调机成本进行计算。

1.3.1 延误成本

式中：N 为机型载客量；T 为延误时间； 延误成本UCdelay设定为每延误一分钟亏损1 200 元；N 基于不同机型而不同。

1.3.2 取消成本

通常情况下航空公司不会轻易取消航班，因为取消航班的成本巨大，并且后续航班很难得到有效的执行，还降低了航空公司的声誉，航班取消的成本表示方法如

式中：N 为机型载客量；P 为综合票价。 N 和P 均可以通过机型求出。

1.3.3 航班的期望恢复成本计算

航班的期望恢复成本由上文的两个个成本组成，如

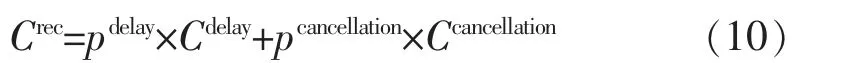
式中：pdelay为延误发生的概率；pcancellation为航班取消发生的概率。 其中由于不考虑换机和调机的情况，则认为换机和调机发生的概率为0[9]，由此可总结为式（11），其中pregular为正常航班的概率。

(1)确保PCL控制系统运用环境干燥。虽然PCL控制系统的环境适应能力较强，但是由于其为电气设备，因此应当保证应用PCL控制系统的环境的干燥，确保PCL控制技术在金矿山电气设备中的安全稳定性。

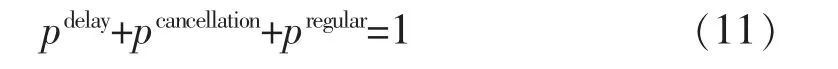
2 基于鲁棒性提高的航班计划优化模型

本模型在时空网络模型的基础上进行了变换，以整体航班计划的鲁棒性最大化为目标，模型参数和变量的含义为：Rf代表航班f 的鲁棒性；F 代表航班集合，f∈F；K 代表机型集合k∈K；S 代表航班链集合，s∈S；Cfopr代表计划运行成本；Cfrec代表期望恢复成本；r 代表航班成本增加比率；Cmin为不考虑鲁棒性的情况下航班计划运行成本最小值；xf为决策变量，当航班被执行时取值为1，反之为0；afs为指示变量，当航班f 在航班链s 上时，afs为1，反之为0；xsk为决策变量， 当航班链s 被选中并且由机型k所执飞时，xsk为1，反之为0；ydk-和ydk+分别代表在整个航班计划中任意时刻前后起飞的机型k 的数量；yak-和yak+分别代表在整个航班计划中任意时刻前后到达的机型k 的数量[9]。

根据以上参数以及变量，建立以下基于鲁棒性提高的航班计划优化模型

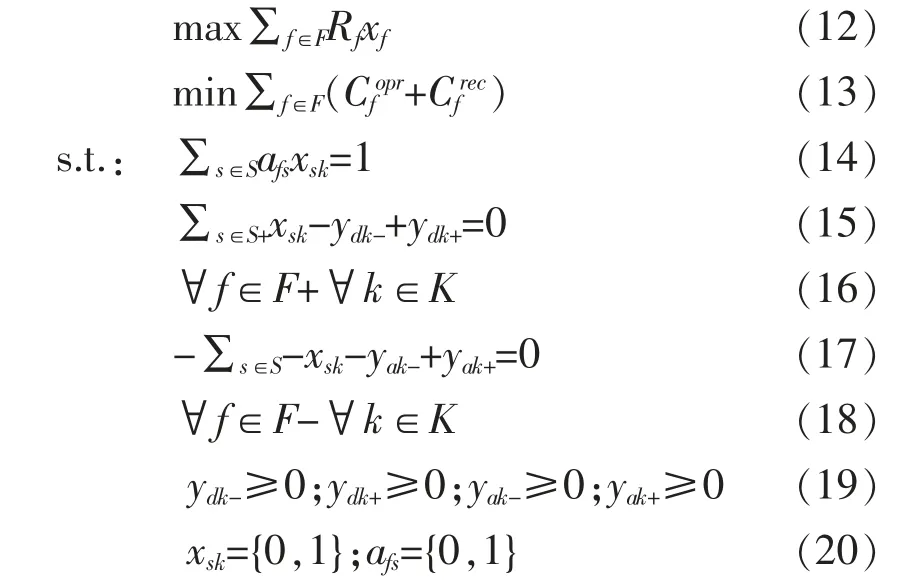
该模型中，式（12）目标函数表示使得整个航班计划鲁棒性最大化；式（13）为航班计划运行成本与期望恢复成本之和最小化；式（14）为航班覆盖约束；式（15）和式（17）为航班网络模型的节点流平衡约束；式（19）和式（20）为变量约束[11]。

3 基于十日航班数据的模型求解

由于模型是双目标函数，在求解过程中有一定的困难，故通过将模型简化为单目标函数来进行计算[12]。 求解思路如图3 所示。

3.1 将双目标函数模型转换为单目标函数模型

由于调整完航班计划后会减少延误的时长，但是变相增加了航班调整和取消的次数， 导致了Cfrec的增加，所以为了防止一味的增加鲁棒性而忽视航班计划成本的增加，将成本的目标函数转为约束以限制成本的无限制增长[13]。 转换后成本目标函数变为以下约束

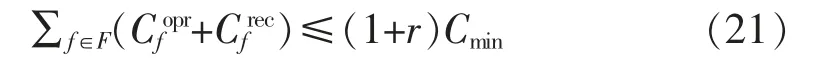
式中：可以发现计算结果与r 的取值直接相关，在理想状态下r=0 时式子无解，即不增加成本而提高航班计划鲁棒性的结果不存在，同时通过航班经验得知航空延误成本一般是总成本的20%～28%， 这里通过取下限20%来约束r 的取值范围为[0,0.2]。

3.2 通过原数据求解Cmin 与Ccancellation

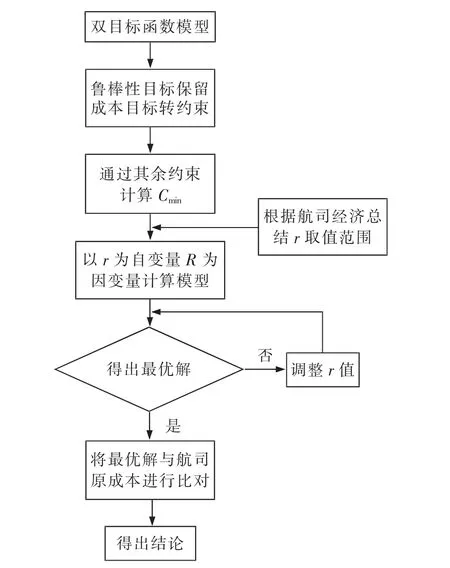
图3 模型求解思路Fig.3 Model solution idea

由于已知某航司在冬春航班上某月十天的航班数据，可以通过第一节里面介绍的方法对每一天的航班运营成本进行计算，因为航司在不计算延误的情况下航班计划是按照最小运营成本制订的，所以可以认为Cmin即为每一天的运营成本[14]。 计算结果如表1 所示。

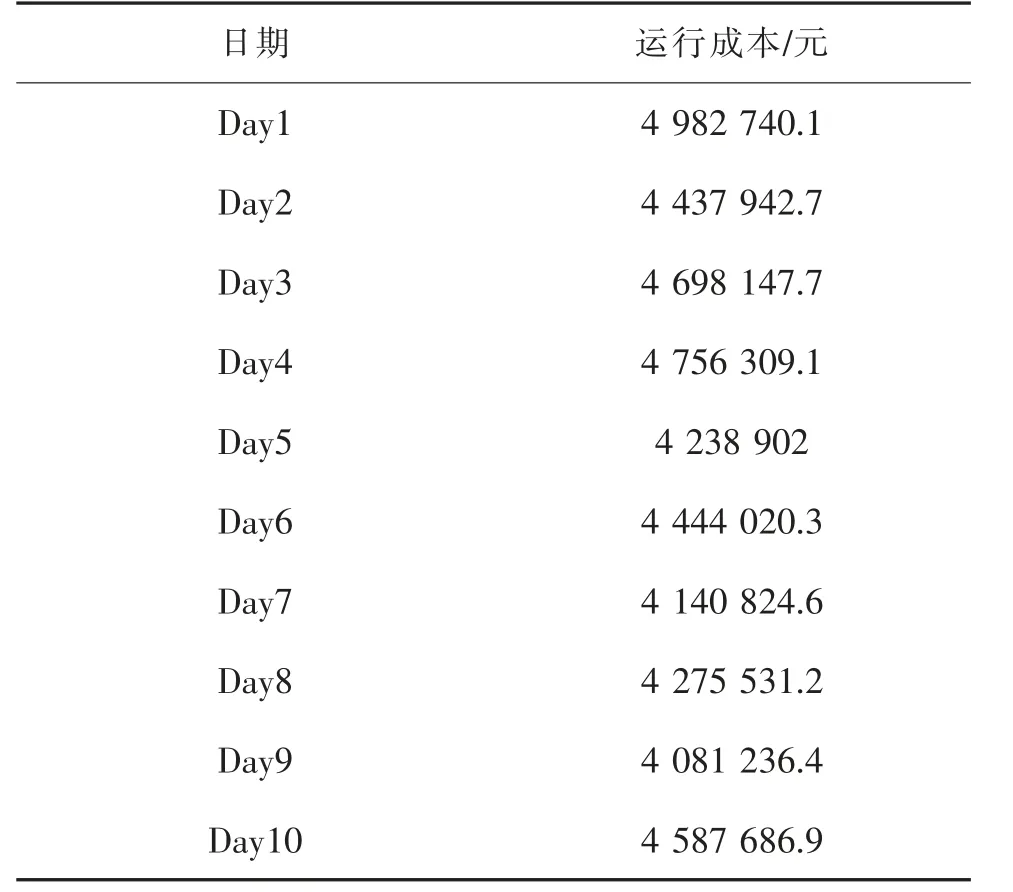
表1 每日最小运营成本Tab.1 Minimum daily operating costs

求出Cmin以后便可以通过Cmin对单目标模型进行求解，目标函数为max∑f∈FRf。

由于已知航班计划的情况下，当前航班计划不考虑延误成本即为航司运营实际最小成本。 故约束式（21）可以简化为式（22）

将约束式（22）带入原模型，即可得到化简之后的模型。 模型如下

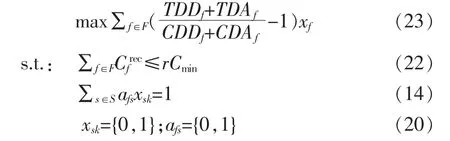
式（23）中的Rf通过第一章里面的公式进行替换；式（14）为航班覆盖约束；式（20）为变量约束。

通过上文的求解Cmin可以发现这10 天之内的航班数量并不相同， 这也是导致每天运营成本差距较大的原因， 对此可以推算出航司已经将所有不适合运行的航班进行了取消， 对此约束式（22）里面的由原式（10）可知×Ccancellation。由于在这10 天中第1 天的运营成本最大，并且航班数量最多， 假定第1 天的航班计划为没有航班取消的情况， 通过观察航班数据得知第4 天也没有产生航班取消情况，其余时间的航班计划均产生了不同程度的取消。 通过式（9）可以计算出Ccancellation，如表2 所示。 其中波音737-800， 波音737-300 和ERJ-145 载客量分别为164，149 人和50 人[15]，综合票价取各个航班票价。pcancellation为这十天内该航班取消的概率。

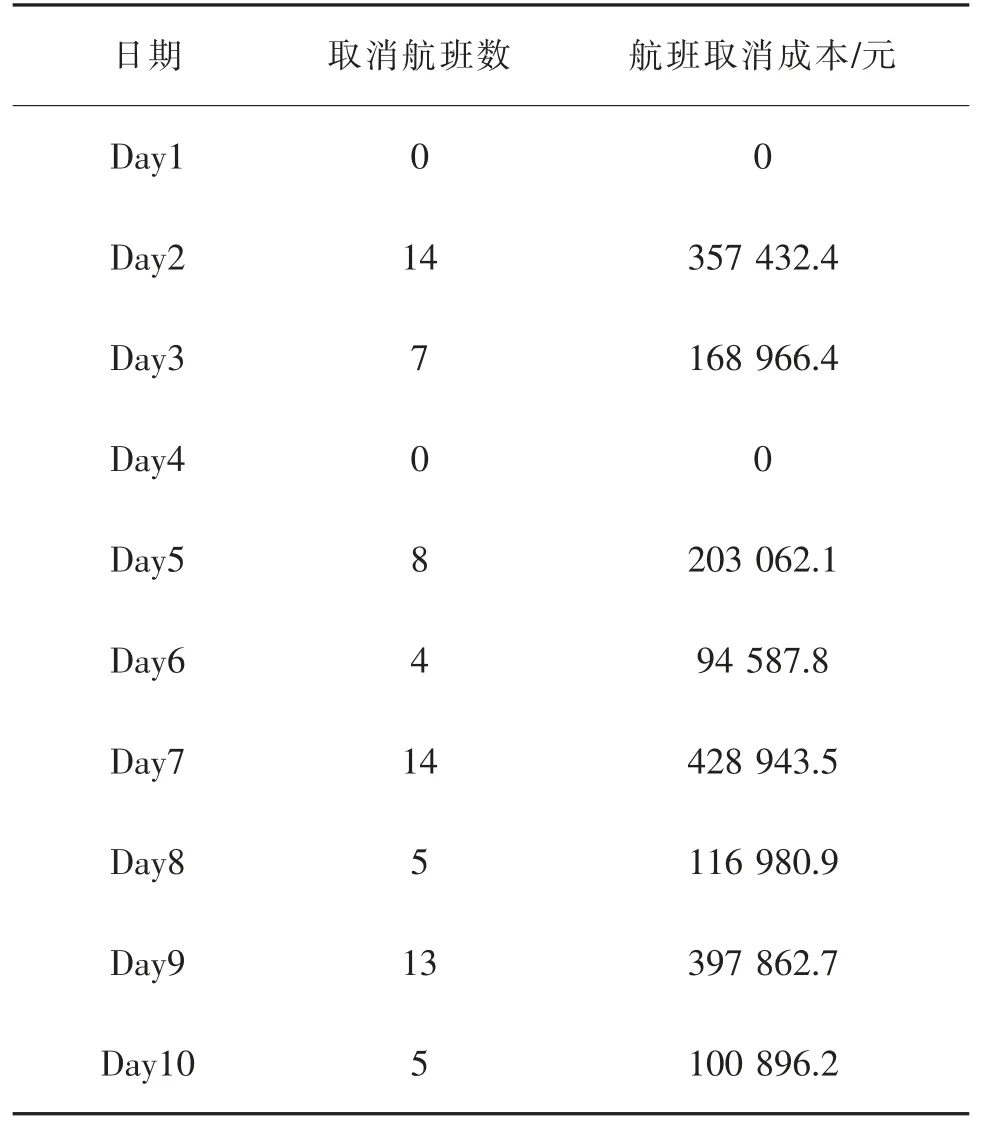
表2 每日航班取消成本Tab.2 Daily flight cancellation costs

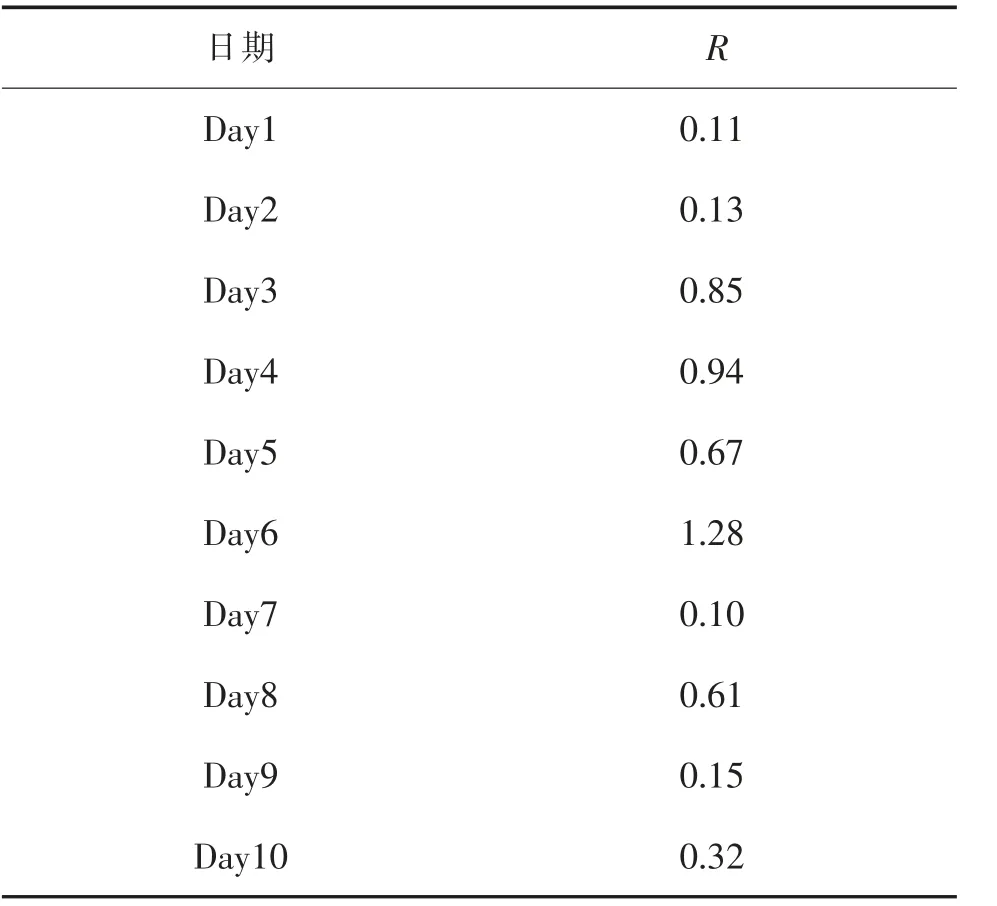
表3 每日鲁棒性Tab.3 Daily robustness

3.3 通过Lingo 软件求鲁棒性最大值

在已知上述条件下， 通过Lingo 进行建模对航班计划鲁棒性进行求解。

通过对Lingo 的求解结果描点作图， 可得到鲁棒性R 随着比率r 变化的曲线图， 这里采用Day1的数据进行作图。 实验结果如图4 所示。

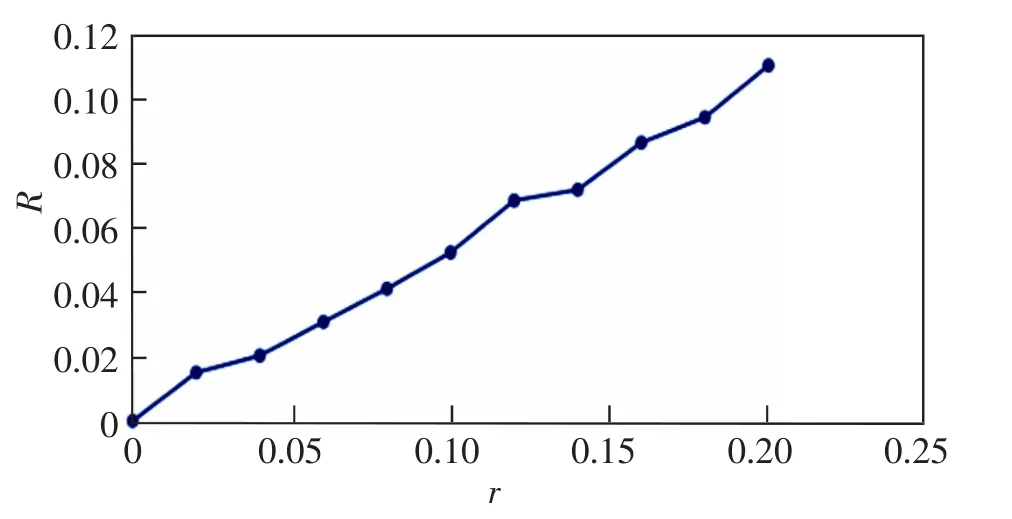
图4 实验结果Fig.4 Experimental results

从图4 可知随着r 的增长， 航班计划的鲁棒性随之增长，并且在r=0.2 时到达最高点。

通过Lingo 计算得到当r=0.2 时10 天的鲁棒性如表3 所示。

根据表3 的结果可以发现在模型优化这10 天中的八天鲁棒性都得到了不同程度的提高。而day7与Day9 的鲁棒性为0.10 和0.15， 结果相较于其他天数较小，通过对数据的观察发现缺少部分航班计划延误时间，导致产生了一定程度的异常。 Day1 和Day6 都没有数据缺失，但是结果差值较大，通过数据观察发现由于Day1 的延误时间最长，而Day6 的延误时间最短，由此可见该模型在较短时间内的延误下可以极大的增加航班计划鲁棒性。

4 结论

1） 航班计划遭遇延误的情况是无法避免的，通过设置模型，将航班计划的鲁棒性最大化，并且通过十日的航班数据来验证模型的正确性。 该模型可以帮助航空公司在制订航班计划时考虑鲁棒性这个因素，从而在设计之初增加过站裕度时间以减少航班延误的发生。

2） 通过功能强大的Lingo 软件建模求解，并将结果绘图，得到了当r=0.2 时鲁棒性最大的结论。

3） 本模型的不足在于没有考虑调机和飞机交换的成本， 导致在计算时会产生鲁棒性偏高的结果，综合考虑所有期望恢复成本并进行建模计算是接下来研究的重点。