基于Kelvin 链率型模型的混凝土徐变有限元计算

2021-04-24陈梦成

华东交通大学学报 2021年1期

杨超，陈梦成

（华东交通大学土木建筑学院，江西南昌330013）

混凝土徐变是指混凝土结构在恒载作用下随时间变化的变形。混凝土徐变计算的理论基础主要包括老化理论[1]、多孔介质理论[2]、黏弹性理论[3]、继效流动理论[4]、固结理论[5]等。基于上述徐变理论，演绎出了各种混凝土结构的徐变分析方法如：初应变法[6-7]、位移增量法[8]、Galerkin 加权残值法、等效模量法[9]、龄期调整有效模量法[10-13]、逐步积分法[14]、全量递推方法[15]、率型叠加算法[16]等。 2001 年Bazant[17]将等效模量法、按龄期调整有效模量法、徐变率法、流动率法及Levi’s & Arutyunian’s 方法等6 种徐变计算方法的计算结果与徐变试验曲线进行比较，结果发现，按龄期调整有效模量法优于其它所有方法。混凝土材料在长期服役过程中，徐变性能因受众多因素影响，目前尚未形成统一、有效的徐变计算方法。

采用Kelvin 链模型将应变Volterra 积分方程转化为率型徐变积分微分方程[18]，在此基础上，引入中间变量离散连续时间，结合应力应变增量弹性本构关系，最终建立含初应变的弹性结构有限元分析模型。最后使用该有限元分析模型，对大型商用有限元软件Ansys 进行二次开发，实现混凝土徐变计算。

1 基于Kelvin 链率型模型的徐变理论

根据微观力学理论[19]，混凝土在工作应力范围内，单轴作用下徐变模型可依据Stieltjes 积分公式，用以下两种Volterra 积分方程形式表示

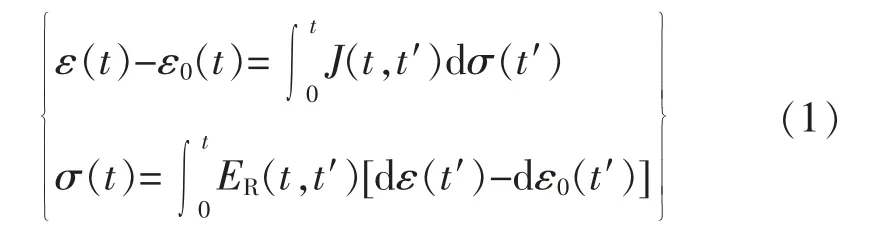
式中：t 为混凝土开始浇筑至徐变计算时间；t′为加载龄期；σ 为混凝土应力；ε 为混凝土应变；ε0（t）为非弹性初始应变（如温度引起的热膨胀和收缩等除作用力以外产生的应变）；J（t，t′）为徐变函数（也称为徐变柔度函数），定义为单位应力作用下，t-t′时间内引起的应变；ER（t，t′）为松弛函数（也称为松弛模量），定义为单位应变作用下，t-t′时间内引起的应力；1/J（t，t′）=ER（t，t′）=E（t）表示为瞬时弹性模量。

徐变函数通过Dirichlet 序列变化[20]可以表示为

式中：τi为黏滞时间（事先给定值），其中i=1，2，…，M；E0为瞬时弹性模量；Di（t′）为龄期相关模量，可以由确切的柔度函数通过最小二乘法拟合得到，也可以由连续黏滞谱[21]确定，在后文给出。

将式（2）代入式（1）中，可得

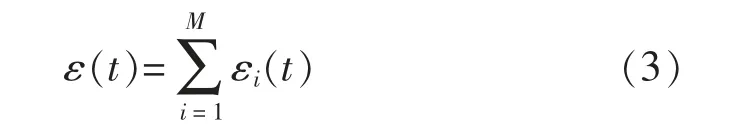
其中

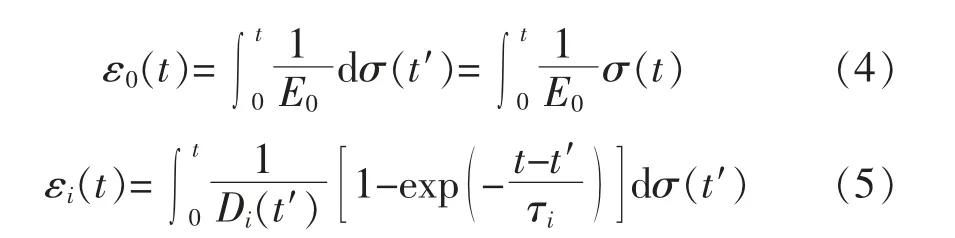
式（3）可以理解为总应变由M+1 个元件的应变累加而成；式（4）理解为编号为“0”、弹性刚度为E0的弹簧元件；式（5）理解为流变模型中的其他M 个Kelvin 黏滞元件。

将式（5）对t 进行微分，得到结合公式（5），可以得到以下积分微分方程

1）考虑非老化情况，满足Di（t′）=Di=常数，式（7）改写为微分方程（率型方程）

由式（8）可得，总的应力可以分为两部分。第一部分为由刚度为Di弹性元件引起的应力；第二部分为ηi=τiDi由线性阻尼为黏滞元件引起的应力，该阻尼元件的应变率为ε˙i。此时对应图1 中的（a）非老化Kelvin 链模型。

图1 Kelvin 链模型Fig.1 Kelvin chain model

2）考虑老化情况。通常情况需要考虑材料的老化。为了消除式（7）中的积分，再次对该式对t 进行微分，得到微分方程（率型方程）

同样，可以采用式（9）来表征具有时变性能的Kelvin 元件（包含其中的弹性元件和阻尼元件）。参考文献[18]，考虑老化时，Ei（t）=Di（t）-τi（t），ηi=τi-Di。此时对应图1 中的（b）老化Kelvin 链模型。

式（8）和式（9）即为不考虑材料老化与考虑材料老化情况下的徐变计算微分方程形式（也称为率型）。在考虑材料老化情况下，为了解上述二阶微分方程，文献[18]提出中间变量使计算便捷有效，引入中间变量

将式（10）代入式（9），即可得到满足初始条件γi（0）=0 的一阶微分方程

在复杂应力状态下，一阶微分方程（11）可改写为

一般来说，微分方程（11）式的解需要对每个时间步Δt（从时刻tn到tn+1）进行积分计算，分析任意步计算时，中间变量γi（tn）=γi（n）的值总是依赖于上一步（如果是第一步，则依赖于初始条件）。根据文献[18]分析，时间步Δt 的选取对计算效率影响很大。当Δt≥τ1时，采用积分算法求解常微分方程所得到的结果是不稳定且精度不高，为此，需要对时间步Δt 寻找其它选择方法。Zienkiewicz 等[22]在分析非老化材料时对时间步Δt 的选取，曾提出了指数法，后来这种时间步Δt 选取的指数法被Bazant[23]延伸到了老化材料中。

指数算法的关键在于当Δt≥τ1时，若微分方程（11）的右边在任意时间步保持为常数，则微分方程（11）可以有解析解。为简便计算，我们先考虑单向应力问题，然后再拓展至复杂应力状态问题。令Δt=tn+1-tn，Δσ=σ（tn+1）-σ（tn），Di（n+1/2）=Di（tn+Δt1/2），则式（11）右边可以写成Δσ/ΔtDi（n+1/2），即式（11）可以表示为

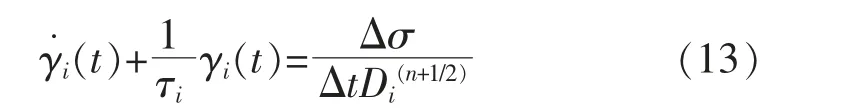
求解常微分方程（13），得到

其中，βi和λi为

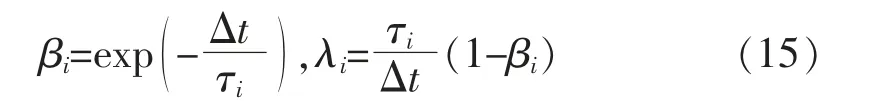
对式（10）积分求出应变增量，根据Kelvin 链模型，对应变增量进行求和可以得到总的应变增量计算公式

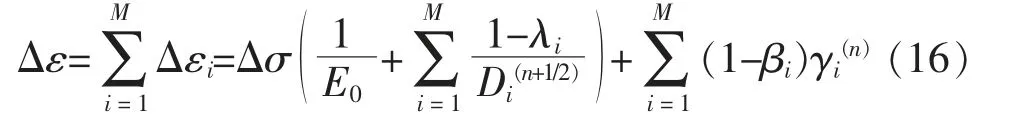
式（16）右边第一项理解为施加应力时引起的弹性应变增量，该弹性应变增量等于弹性应力增量乘以等效弹性柔量。等效弹性模量表示为

式（16）右边第二项理解为恒载引起的徐变应变增量

为方便有限元子程序编写，式（16）可以改写为

将式（19）代入公式（14），中间变量可以由下式更新计算

以上算法适用于单向应力情况，但是也很容易通过乘以各项同性材料矩阵CV应用至复杂应力情况（即三维情况）。

基于Kelvin 链模型的计算连续黏滞谱有[21]

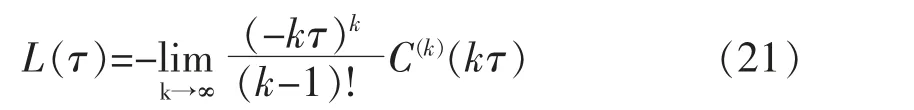
式中：C（k）（kτi）为徐变函数C（t，tn-1/2）k 阶导数；C（t，t′）=J（t，t′）-1/E0；当k=3 的时候，计算可满足精度要求[21]。将连续的黏滞谱离散得到离散的黏滞谱

2 Ansys 有限元软件中Usermat 子程序的算法设计

基于Kelvin链率型的混凝土徐变计算方法式（19），采用64 位Ansys15.0+Vsiual Studio 2010+Inter Fortran Composer XE 2013 SP1 对用户材料子程序Usermat 进行二次开发，算法流程图如图2 所示。具体计算步骤如下。

1）说明Ansys 有限元软件中Usermat 子程序所需要的常数、变量、变量数组。

2）从Ansys 主输入数据中读取材料常数，包括弹性模量、泊松比、加载龄期等。

3）在三维复杂应力情况下，定义CV和雅克比矩阵D=E0CV。

4）离散时间tn，n＝1，2，…；Δt=tn-tn-1；tn-1/2=t0+[（tn-t0）（tn-1-t0）]1/2；当n=1 时，t1/2=（t0-t1）/2，t0为加载龄期，开始时间步循环步。

5）当计算时间小于加载龄期t0时，按式（6）计算瞬时加载弹性变形，否则（即当t 超过加载龄期t0时）按式（7）计算持荷过程中徐变变形。

6）初始化应力增量，按弹性结构计算初应变增量Δε。

7）按照率型徐变拟线弹性应力应变关系计算任意时刻徐变变形：

8）循环计算下一分析步，当增量步达到设置的最大值时结束计算。

图2 基于率型徐变模型的有限元徐变分析算法流程图Fig.2 Flowchart of finite element creep analysis algorithm based on rate-type creep model

3 标准算例

算例1 计算恒定轴压荷载作用下素混凝土方块徐变[24]。素混凝土28 d 弹性模量E28=30 MPa。混凝土龄期为7 d 时，方块顶面施加1 MPa 恒定应力，随后保持荷载恒定30 年左右。本节有限元模型数值解与及现有结果[24]对比情况如图3（b）所示。比较结果表明，三者结果几乎一致。

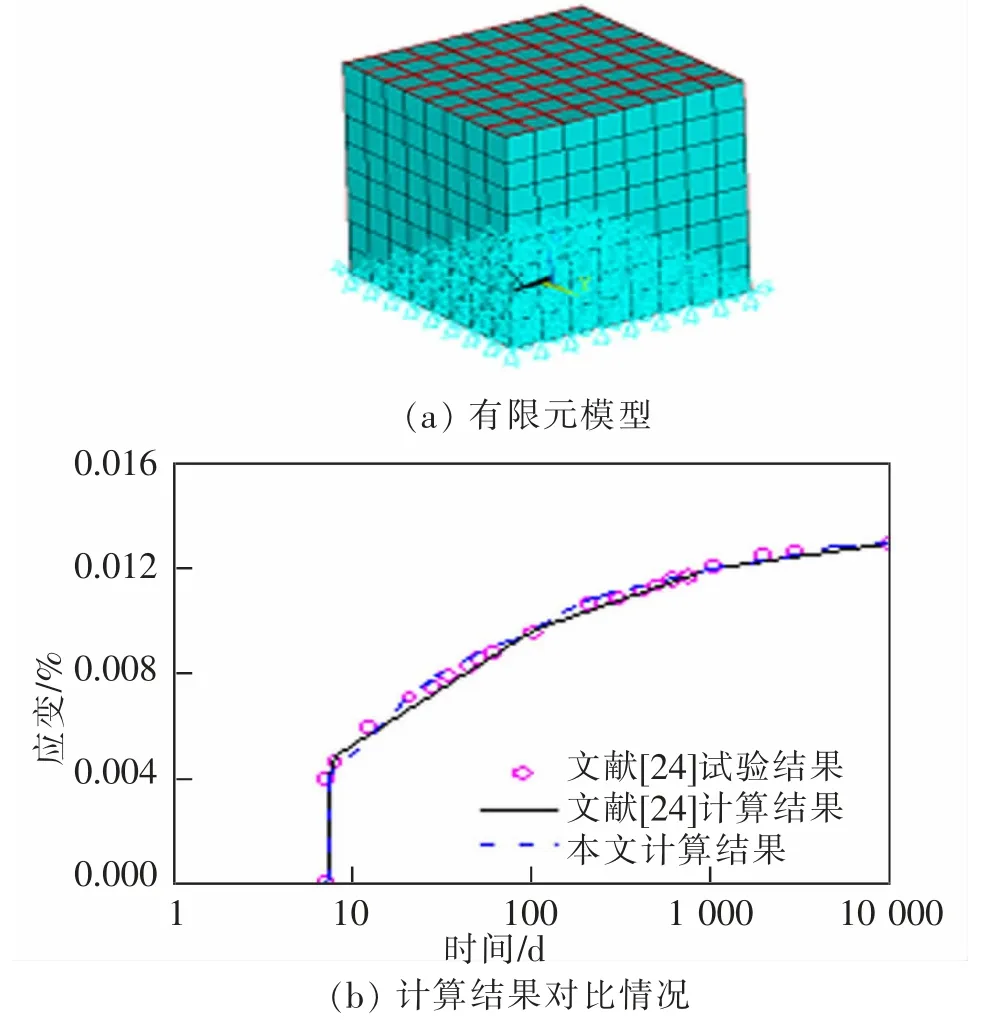
图3 素混凝土方块有限元模型及计算结果对比图Fig.3 Finite element model and calculation results comparison of plain concrete brick

图4 素混凝土长柱有限元模型及计算验证Fig.4 The finite element model and calculation validations of plain concrete long column

算例2 计算逐步施加轴压荷载的素混凝土长柱徐变[24]。素混凝土强度fc28=30 MPa，相对环境湿度h=70%。混凝土龄期为7 d 时，柱端面进行第一次加载，应力值为1 MPa；随后每隔7 d 对柱端面叠加1 MPa 应力；叠加次数共12 次；叠加完成后，保持荷载恒定约30 年。有限元计算模型如图4（a）所示，本节有限元模型数值解与及现有结果[24]对比情况如图4（b）所示。比较结果表明，三者结果几乎一致。