基于VMD-LSTM 轨道交通客流预测模型

黄海超，陈景雅，孙 睿

（河海大学土木与交通学院，江苏 南京210098）

由于轨道交通安全、准时和环保等特点，已逐渐成为人们出行的首选交通方式，基于数据挖掘技术的客流量预测是城市智能交通系统的重要组成部分，不仅对人们出行和智能交通管控有着重要的指导意义，也有助于相关部门提前进行运营规划和调度。

客流量预测模型主要分为以差分自回归移动平均模型[1]（ARIMA）和灰色模型（GM）为代表的参数模型与以支持向量机[2]（SVM）和神经网络[3]为代表的非参数模型。 但传统模型收敛慢，时效性低，很难满足交通大数据情况下智能管控需求[4]。 基于深度学习的长短时记忆神经网络LSTM （long shortterm memory）不仅预测性能、收敛时间优于传统参数[5]与非参数[6]预测模型，偏差分布波动与预测鲁棒性也明显优于传统预测模型[7]；针对非平稳的客流量数据，经验模态分解[8]（EMD）、集成经验模态分解[9]（EEMD） 被用于降低样本噪声干扰并有效提高预测精度。 变分模态分解（variational mode decomposition，VMD）作为最新提出的分解算法，虽然在交通领域应用较少，但在电力荷载[10]、期货[11]等领域已证明其对非平稳信号良好的处理能力。

目前研究大多集中于短时客流量预测[12]（15 min内），然而过短时间的预测不能为人们出行规划预留充足时间，提供有价值的出行指导。 为此，文章创新性地将VMD 引入客流量预测领域，降低客流量信号的非平稳性，结合深度学习的LSTM 进行预测，提出VMD-LSTM 预测模型，实现对每小时轨道交通客流量的准确预测，提高LSTM 神经网络的预测性能。

1 VMD-LSTM 神经网络预测模型构建

1.1 VMD 分解原理

VMD 是一种全新的自适应、完全非递归时频信号分解算法，通过构建变分模型，将原始时间序列s（t）分解为不同的具有有限带宽的分量uk（t），对应的中心频率为ωk，交替迭代更新寻找约束变分模型的最优解，在此过程中实现本征模态函数IMF 的有效分离，克服了EMD 存在端点效应和模态分量混叠的问题，其算法可表示为[13]

1） 对每一个uk（t）进行Hilbert 变换得到单侧频谱

式中：δ（t）表示Dirac 分布函数；*表示卷积运算。

2） 通过将每个模式的分析信号乘以估计的中心频率e-jωkt，将频谱移到基带

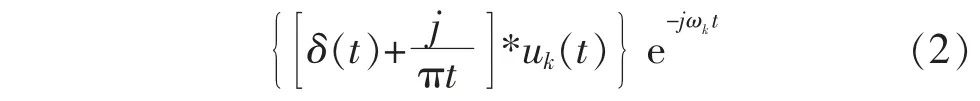
3） 通过对解调信号梯度的L2 正则化进行高斯平滑估计，得到各模态函数的带宽，约束变分模型可表示为

式中：∂t表示求偏导；k 为分量的个数。

1.2 LSTM 神经网络

LSTM 是深度循环神经网络的代表，通过门的开关实现时空记忆功能，能有效解决循环神经网络的梯度消失和爆炸问题。 通过引入一个门控单元系统，可以控制何时忘记历史信息或使用新信息更新单元状态， 使LSTM 在解决非线性时间序列问题时效果极佳[14]，其过程可表达为

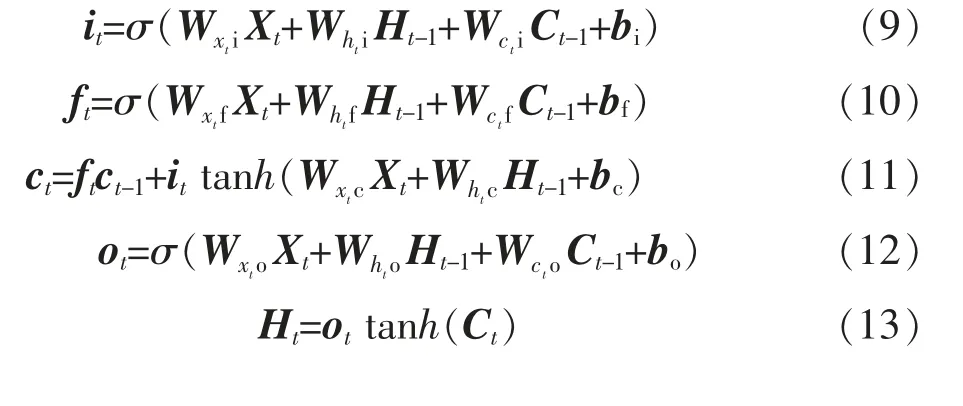
1.3 VMD-LSTM 预测模型

VMD-LSTM 预测模型建立主要分为两部分。 第一部分为数据预处理，首先将对原始数据中的重复、异常、 缺省值进行清洗获得时序客流量数据。 基于VMD 分解原理，设定合适的超参数，将非平稳的每小时客流量数据分解为本征模态函数IMF 和余量信号R（t），弱化样本噪声干扰；第二部分为分量预测，首先选择LSTM 神经网络时间步长、 输入层隐藏层神经元个数等基本参数，确定神经网络的训练方式与代价函数，获得网络拓扑结构。 建立与分解分量个数相同的LSTM 神经网络，对分量分别进行预测，获得仿真本征模态函数（SimIMF）最后将各预测值进行重构获得最终客流量预测值， 并与真实客流量进行比较，评价模型性能。 模型建立流程如图1 所示。

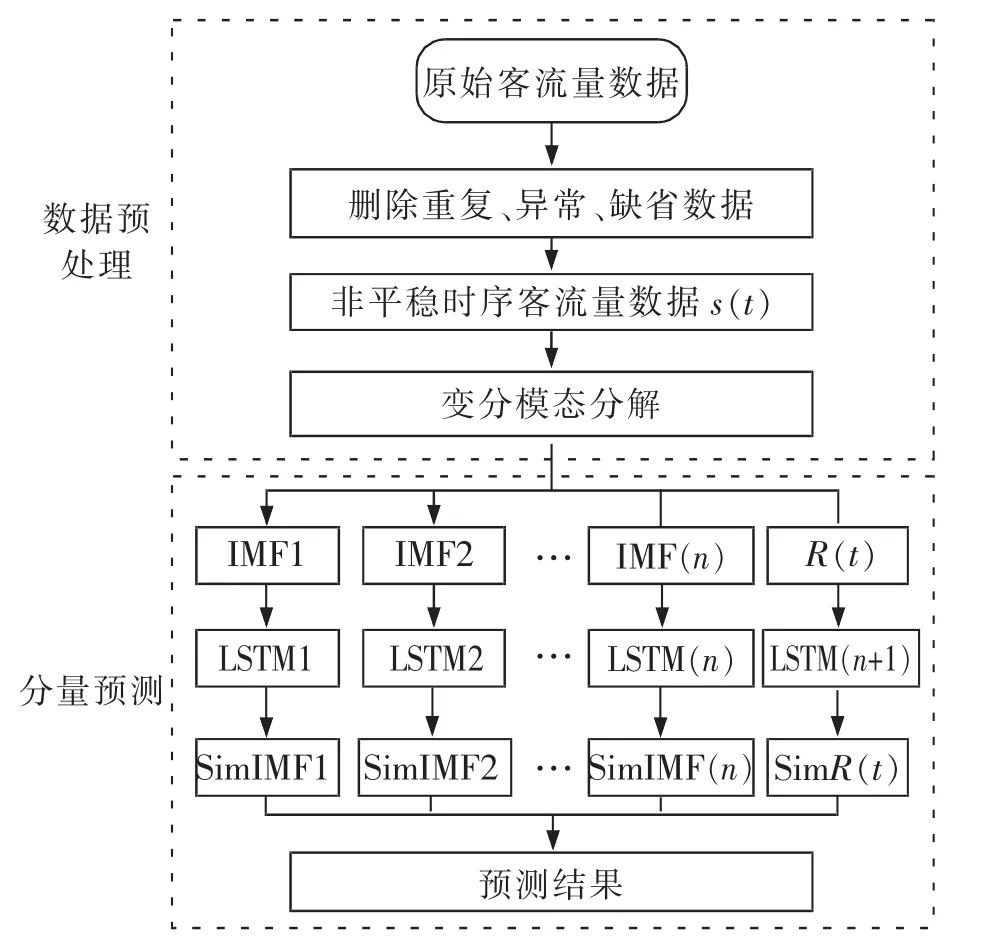
图1 VMD-LSTM 神经网络模型流程图Fig.1 VMD-LSTM neural network model flow chart

2 应用实例

2.1 数据预处理

采集明尼苏达州明尼阿波利斯至圣保罗301站台2017 年每小时轨道交通客流量，明尼阿波利斯与圣保罗分别是明尼苏达州第一、 二大城市，旅客往来频繁，客流规模大；301 站台为圣保罗通往明尼阿波利斯及其他城市的主要站台，人员出行规律复杂，因此采用该站台作为研究对象。 对轨道交通数据中的异常数据进行预处理。 包括完全相同的记录、明显异常的记录及缺失的记录，数据清洗后共获得10 605 条时间数据。 由于数据样本较大，有效避免了机器学习过程中预测模型对个别样本的偏好，无需对样本进行抽样训练。

采用VMD 算法对非平稳交通量时间序列数据进行分解时，由于VMD 在轨道交通客流量预测领域应用较少，缺乏先验知识确定超参数。 综合考虑重构误差与中心频率分布，二次罚因子α 取1 000，分解模态数K 取11。分解得到10 个IMF 分量以及一个余量信号R（t），分解结果如图2 所示。 分量频率由高到低进行排列，更加清晰的呈现原始客流量数据在不同时间尺度下的变化规律，其中高频信号表示客流量变化的细节，含有大量样本噪声；低频部分则表征客流量的趋势，频率最低的余量信号R（t）也称为趋势项，表征全年轨道交通客流量的波动趋势。

2.2 神经网络模型构建

选择前10 个月（8 880 条时间数据）作为训练集，最后两个月（1 725 条时间数据）用于测试模型性能。 时间步长取4，隐含层数取1，隐含层神经元个数取200；迭代次数取250。初始学习率设为0.01，同时为防止学习率过大，模型来回震荡，采用衰减法动态调整学习率，每迭代50 次学习率衰减50%。损失函数采用均方根误差，通过AdamOptimizer 优化器对模型进行优化， 得到LSTM 神经网络的拓扑结构。

根据以上参数，建立11 个LSTM 神经网络，对分解获得的分量分别进行训练、预测，根据VMD 算法对预测结果进行重构，得到最终每小时客流量预测值。 并绘制总体预测残差，如图3 所示，可以看出LSTM 神经网络仅在初期前1%数据范围内预测误差较大，随后残差迅速变小并趋于稳定，表现出良好的鲁棒性。

同时为验证VMD-LSTM 神经网络模型的性能，分别与LSTM 神经网络、随机森林（RF）、支持向量机（SVM）进行对比。 对比模型与原模型采用相同的参数设置，RF 预测模型利用经验公式确定子树数目为103，SVM 预测模型采用自适应算法搜索最佳超参数c，g，预测结果如图4 所示。

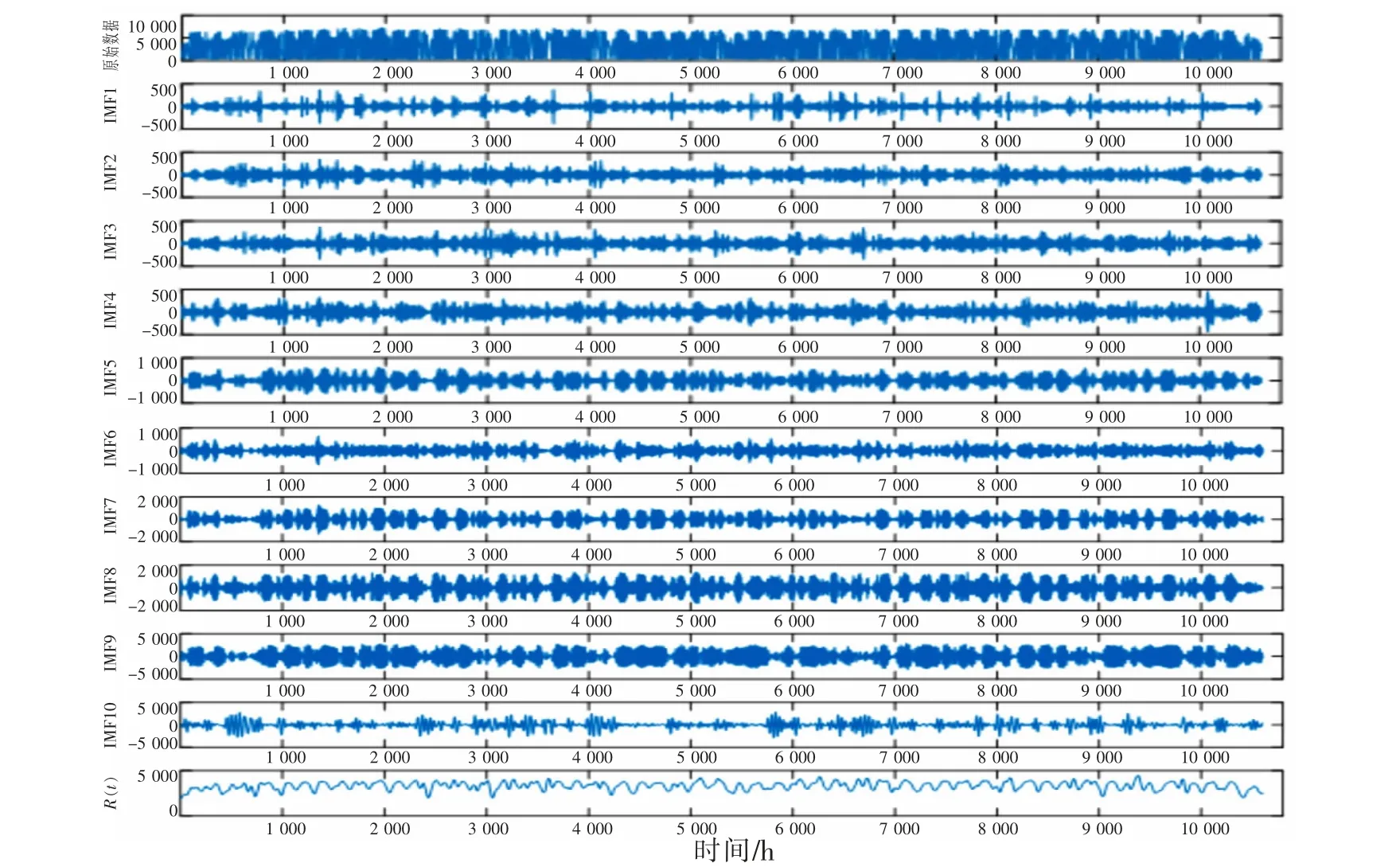
图2 客流量数据VMD 分解结果Fig.2 VMD decomposition results of passenger flow sequence

图3 预测残差Fig.3 Predicting residual

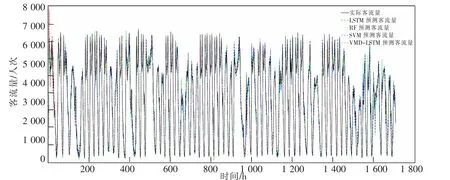
图4 神经网络模型对比Fig.4 Comparison of neural network models

平均绝对百分误差（MAPE）体现了真实值与预测值的相对偏差，可直接衡量预测结果的好坏，常被用于评价预测模型的优劣，但不能直观反映真实值与预测值的差值。 均方根误差（RMSE）可直接体现真实值与预测值的绝对差值，且特大或特小误差对指标影响明显，可有效弥补MAPE 的不足，相关系数（R）可用于表征真实值与预测值变化趋势的相似程度。 分别采取以上指标对各预测模型性能进行评价，结果如表1 所示。

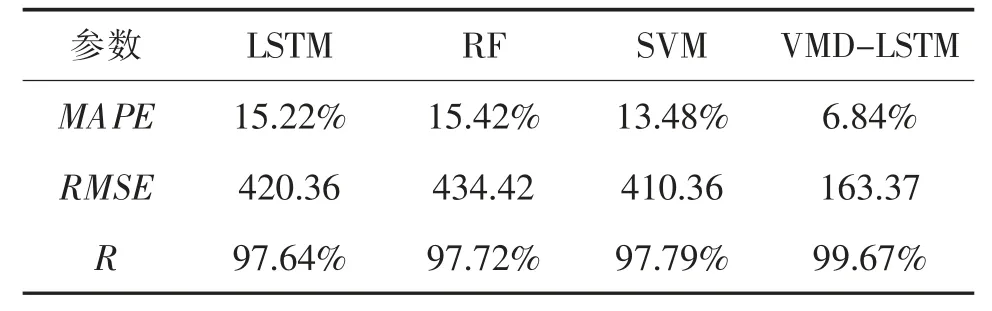
表1 经典预测模型性能对比Tab.1 Performance comparison of classical prediction models

结合图4 和表1 可以看出，在轨道交通客流量数据样本足够大的情况下，所有预测模型均有极高的预测精度。传统的时间序列预测模型RF，SVM 与基于深度学习的LSTM 预测误差相差不大。 但LSTM 神经网络克服传统预测模型每次加入新数据，需要重新训练的缺陷，收敛速度也有较大提高，体现神经网络良好的综合性能。

当采用VMD 优化LSTM 后，预测误差显著降低，VMD-LSTM 模型的预测精度相对三种对比模型总体有了较大提高。 对比传统时间序列预测模型RF，SVM，MAPE 分别减小了8.58%，6.64%，RMSE分别减小了271.05，246.99； 相比LSTM 神经网络，MAPE 减小了8.38%，RMSE 减小了256.99，R 值也有一定的提高。 这是因为VMD 将含噪声的客流量数据分解成模态分量与余量信号，将含噪声的高频信号单独分离出来，从而弱化样本噪声对总体预测精度的干扰，有效提高神经网络的预测精度；同时使非平稳客流量数据转换为多个平稳时间序列，LSTM 神经网络对这些平稳信号进行预测，进一步提高模型的鲁棒性。

3 结论

1） 采用VMD 将含噪声的轨道交通客流量数据分解成具有原始数据局部特征的不同频率信号，降低噪声对模型的干扰，提出VMD-LSTM 神经网络预测模型。

2） 采用明尼苏达州轨道交通数据验证VMDLSTM 预测模型性能，结果表明VMD 改进LSTM 能显著提高神经网络的预测精度与鲁棒性，预测误差相对传统预测模型更小。