基于改进型梯度法的客车侧翻一步碰撞算法精度改进研究＊

王童 陈轶嵩

（长安大学，西安 710064）

主题词：客车 侧翻碰撞 一步算法 改进型梯度法 局部摄动思想

1 前言

侧翻是客车最严重的事故类型之一，往往造成群死群伤的严重后果[1]。客车侧翻碰撞安全性能主要通过有限元仿真软件模拟和优化。目前常用的侧翻碰撞安全性仿真软件LS-DYNA、PAM-CRASH、DYTRAN 等，都是以非线性动态显式积分算法为基础，主要采用中心差分格式，计算时间过长，分析结果受工程师的经验和知识水平影响较大，严重影响计算效率，增加了开发成本[2]。

客车侧翻一步碰撞算法是参考板料冲压一步成形算法思想[3-5]提出的一种用于客车侧翻碰撞的新算法。针对板料冲压一步成形算法，王鹏等人通过应用基于塑性变形理论的一步有限元方法模拟金属成形过程，快速预测了最终坯料形状及应力应变分布情况[6]。借鉴该算法的核心思想，侧翻一步碰撞算法同样基于非线性全量理论，并利用了侧翻碰撞过程中的能量转换关系，与现有LS-DYNA 等增量法软件相比，在略微牺牲计算精度的情况下，大幅提升了计算效率。算法可在车身设计初期对结构侧翻安全性进行快速评价，缩短产品开发周期[7]。

为获得结构最终变形，算法根据车身侧翻碰撞过程运动变形特点和能量转换关系对满足变形条件的初始解进行预测，再采用牛顿-拉夫森（Newton-Raphson）法迭代求解[8]，得到结构的最终变形。由于传统的Newton-Raphson 方法在平衡迭代过程中需对有限元平衡方程进行求解，且需考虑节点约束对切线刚度矩阵的影响，同时，在每次平衡迭代时，均需对所有节点进行广义失衡力计算，极大影响了求解效率与计算稳定性。

本文基于改进型梯度法[9-11]，对侧翻一步碰撞算法的Newton-Raphson 平衡迭代过程进行改进，并将局部摄动思想引入基于改进型梯度法的广义失衡力迭代过程[12]。在每次平衡迭代中，无需计算切线刚度矩阵，且无需对所有节点进行广义失衡力梯度计算，以期在保证算法模拟精度的同时，大幅提高计算效率。

2 客车侧翻一步碰撞算法基本理论

客车侧翻一步碰撞算法的计算原理为：基于非线性全量理论和比例加载假定，依据ECE R66 法规，忽略中间状态和构形变化，只考虑结构碰撞开始和最大变形2 个状态。根据车体侧翻碰撞过程运动变形特点和能量转换关系，得到满足变形条件的初始解，并采用Newton-Raphson法迭代求解，快速获得结构最终变形。

将碰撞开始状态的结构作为原始构形{X0}。此时车体未发生变形，结构动能Ed为：

式中，M为车体质量；Δh为车体重心下降高度；J为车体绕固定转轴的转动惯量；ω为车体角速度。

碰撞开始状态结构各节点的速度{v0}由式（2）计算：

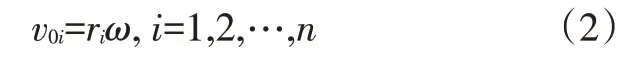
式中，ri为各节点到侧翻假定转轴的距离；n为节点数量。

在结构最大变形状态，车体结构明显变形。侧翻一步碰撞算法中，结构的最大变形是不确定的，因此需假定一个最大变形构形{x0}。此刻各节点位移{U0}为：

忽略碰撞过程中能量的微量增加，认为车体动能Ed在碰撞中主要转换为结构形变能W：

式中，ε为单元应变；σ为单元Cauchy 应力；Ve为单元体积；V为积分体积；N为单元数量。

判断此刻的结构形变能W与车体动能Ed是否相等。若不相等，则对节点位移{U0}进行修正，按照式（4）重新计算结构形变能；若相等，则将节点位移{U0}作为Newton-Raphson迭代初始解。

由于车体结构在空间内变形过程无外力作用，满足能量转换关系的初始解{U}，节点广义失衡力{R(U)}已处于不平衡状态：

式中，{Fext(Ui)}为节点外力；{Fint(Ui)}为节点内力。

应用Newton-Raphson 法，解决节点广义失衡力的不平衡问题。对初始解{U}按式（6）迭代求解，使式（5）达到平衡，得到结构的最终变形：

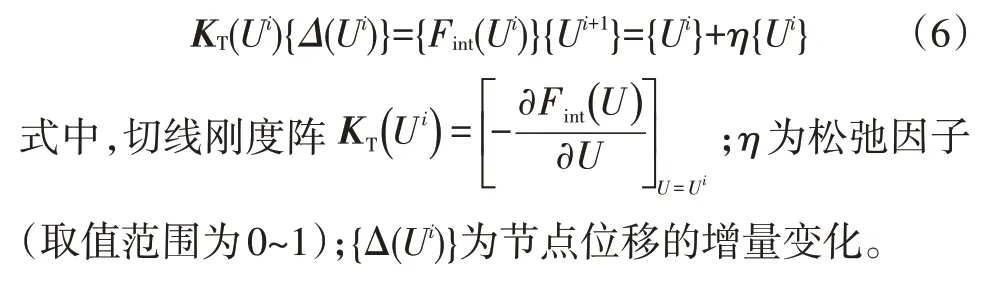
3 改进型梯度法在侧翻一步碰撞算法中的应用

由于Newton-Raphson 法每次迭代均需求解有限元平衡方程，增加了算法的计算时间。为提高平衡迭代效率，本文应用改进型梯度法对算法进行改进，对初始解各节点广义失衡力进行平衡迭代。

首先计算各节点的广义失衡力及其梯度，通过对节点广义坐标作微小扰动，寻找各广义失衡力梯度下降方向，迭代计算至广义失衡力范数达到极小值，即结构内力平衡。接着，将局部摄动思想引入广义失衡力迭代过程，每次有针对性地对部分节点进行扰动与平衡迭代，使广义失衡力范数快速收敛至极小值，获得最终变形。

3.1 节点广义失衡力计算

结构各节点在空间坐标系内均有6个自由度，对应6 个广义力：沿3 个坐标轴方向的节点力Fx、Fy、Fz，及绕3个坐标轴方向的节点力矩Fxx、Fyy、Fzz。

首先求解塑性变形条件下单元局部坐标系内的广义节点失衡力{rie}：

3.2 改进型梯度法的引入

3.3 局部摄动思想的引入

经研究发现，在平衡迭代过程中，对局部节点的广义坐标作微量修改时，仅会引起与其相关的若干节点的广义失衡力变化，其他无关联节点不发生变化。而应用改进型梯度法进行广义失衡力平衡迭代时，在每个迭代步均需计算结构所有节点的广义失衡力及其梯度，加大了算法的计算工作量。在保持计算精度的前提下，为了进一步提高计算效率，本文将局部摄动思想引入基于改进型梯度法的节点广义失衡力的平衡迭代过程。

仍以节点j0为例，在空间坐标系下，对其广义坐标作微量修正(Δuj0x,Δuj0y,Δuj0z,Δuj0xx,Δuj0yy,Δuj0zz,)，扰动后的节点位置如图1 所示。因节点j0为A、B、C、D 4 个单元的公共节点，当节点j0的广义坐标发生变化时，该节点及相关4个单元各节点j1～j8的广义失衡力也发生变化，而其他无关节点的广义失衡力没有变化。节点j0的广义坐标经过微量修正后，结构广义失衡力向量{R}发生变化：

式中，{ΔRj0}为节点j0引起的广义失衡力改变向量。

由节点j0引起的广义失衡力改变向量{ΔRj0}为：

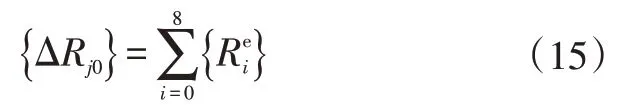
图1 节点j0的局部摄动

为计算节点j0广义坐标改变后的各自由度广义失衡力梯度，本文以X轴方向的位移修改为例，梯度为：

相应的广义失衡力梯度因子可由式（12）计算，进行式（13）的平衡迭代过程。

由上述分析可以看到，应用局部摄动思想进行广义失衡力平衡迭代时，每次迭代实际参与计算的节点数量与结构所有节点相比，几乎可忽略不计，算法的计算量进一步得到大幅缩减。将局部摄动思想引入基于改进型梯度法的节点广义失衡力平衡迭代过程，在保证算法计算精度的同时，进一步提高了计算效率。

4 应用实例

本文以某款长12 m的公路客车的典型车身段作为分析对象，应用本文提出的侧翻一步碰撞改进算法进行模拟，并与原始算法仿真结果及侧翻试验结果进行对比，以检验所提方法的实际应用效果。

图2所示为典型车身段的有限元模型，共包括离散四边形单元234 286 个，节点232 583 个。材料性能参数采用Holloman幂次硬化法则，强化系数k=710 MPa，应变硬化指数t=0.2，初始应变ε0=0，厚向异性系数r=1.3。

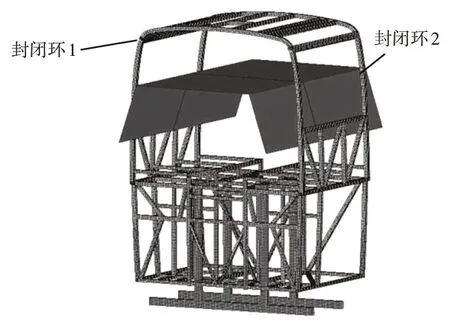
图2 典型车身段有限元模型

图3 所示为基于改进型梯度法的侧翻一步碰撞算法（以下简称“改进算法”）模拟的结构最终变形云图，图4为原始算法模拟的结构最终变形云图，图5为侧翻试验结果。

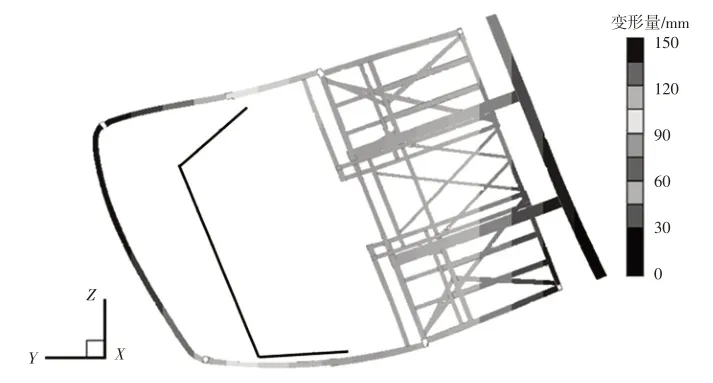
图3 改进算法模拟结构变形

图4 原始算法模拟结构变形

图5 侧翻试验结构变形

选取典型车身段的封闭环1和2两侧立柱内侧的若干测点进行数据采集，如图2所示，则上述3种方式中各立柱的变形量如表1所示。

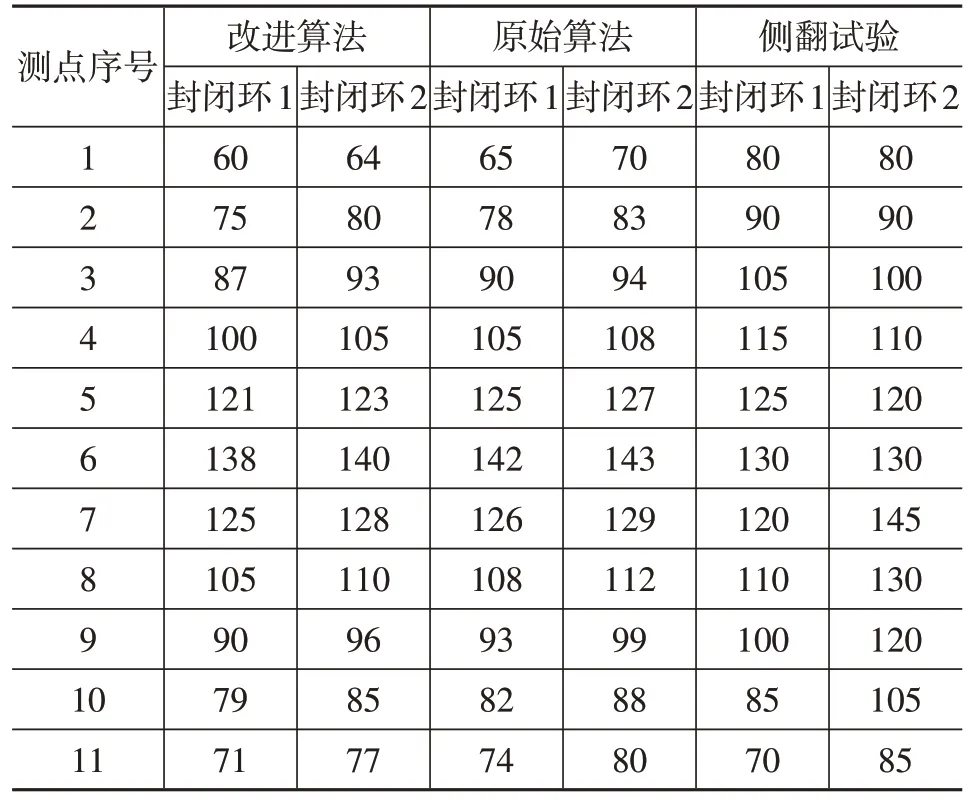
表1 各封闭环两侧立柱变形量统计 mm

通过分析对比发现，3种结果中各测点的数据走势基本一致。将改进算法及原始算法各测点的计算数据和侧翻试验的数据进行对比，分别进行误差计算，并分别对22 个测点获得的误差数据求平均值，发现改进算法的模拟结果与原始算法仿真结果的平均误差相接近，且均小于15%，精度在结构碰撞大变形有限元计算误差可接受的范围内。但改进算法和原始算法的计算时间分别为6 min 和20 min，在基本保证算法计算精度的同时，大幅提升了计算效率，验证了本文所提出的方法在实际应用中的有效性。

5 结束语

本文基于改进型梯度法，对客车侧翻一步碰撞算法进行了改进，并将局部摄动思想引入基于改进型梯度法的节点广义失衡力平衡迭代过程，在保证算法模拟精度的同时，进一步提高了算法的计算效率。

由于在空间坐标系内，各节点广义失衡力均有6个分量，即3个失衡力及3个失衡力矩，在应用改进型梯度法进行节点失衡力平衡迭代时，对失衡力及失衡力矩同时进行了考虑，而力与力矩因量纲不同，可能会对计算效率及结果产生一定影响，需在后续研究中作进一步探索，继续对算法进行完善。