动态载荷作用下UGS管柱非线性屈曲特性研究*
2021-04-23闫行闫怡飞闫相祯
闫行 闫怡飞 闫相祯
(1.中国石油大学(华东)储运与建筑工程学院 2. 中国石油大学(华东)机电工程学院)
0 引 言
注采管柱作为地下储气库(Underground Gas Storage ,UGS)运行的主要工具,面临地质构造复杂和大流量强注强采的苛刻要求,服役周期管柱的非线性屈曲特性研究是储气库井安全运行的关键问题[1-4]。在储气库井作业过程中,井下压力波动和井身结构等产生的持续动态载荷诱发注采管柱振动位移,易导致变形管柱与套管壁碰撞接触,加剧管柱的变形失效。因此,对动态载荷作用下UGS管柱屈曲特性研究显得尤为必要[5-7]。国内外许多学者对储气库井的管柱屈曲做了大量研究。A.LUBINSKI等[8]对轴压及内外压作用下油管的螺旋弯曲进行了研究,发现了管柱失稳的诱因。练章华等[9]采用 ANSYS模拟分析了高温高压超深气井管柱屈曲形态,获得油管-套管接触压力分布情况。张强等[10]通过慢动力法和有限元计算,对悬挂管柱静力屈曲演变进行了分析。石小磊等[11]建立井口抬升高度预测模型,研究了深水条件下高温气井井口抬升的螺旋屈曲效应。刘祥康等[12]通过有限元模型对热生产等工况下全井管柱的屈曲行为进行研究,发现超深气井管柱产生了不均匀的屈曲变形。
上述文献对管柱屈曲进行了深入研究,为UGS管柱安全生产的进一步研究奠定了良好基础。但国内已建UGS主要以深井和超深井为主,管柱处于复杂的力学工况,以上研究成果未充分考虑作业过程储气库井动态载荷对管柱受力变形的影响,尤其是在UGS井高速气流下特定工况的变形分析,已有研究成果无法完整或准确地描述管柱的非线性屈曲特性。针对上述问题,本文根据储气库井筒结构特点,建立了柔性约束下储气库井管柱非线性屈曲力学模型,采用慢动力法阶跃式施加管柱外载荷,并结合考虑接触的管柱屈曲动力学方程,分析动态载荷作用下管柱的非线性屈曲行为和临界载荷。以UGS-ZY11井现场数据为例,通过ABAQUS模拟计算进行对比研究,并分析储库井产量和管径等因素对管柱非线性屈曲的影响,从而获得动态载荷作用下管柱屈曲演变过程和套管接触压力分布特点。研究结果为深入开展动态载荷作用下UGS管柱非线性屈曲特性研究提供了一种新的思路和方法。
1 柔性约束下UGS管柱力学模型
基于弹性力学和管柱力学相关理论,建立柔性约束下UGS管柱非线性力学模型[13],如图1所示。图1中Ft为管柱上端施加的悬挂拉力,Fb为约束反力,Fhk为环空压力。

图1 柔性约束下UGS管柱非线性力学模型Fig.1 Nonlinear mechanical model of UGS string under flexible constraints
UGS井筒内管柱存在上部悬挂,底部放置封隔器等固定约束限制。在正常作业过程中,管柱受自重、气体流动载荷和环空压力等动态载荷作用,导致底部封隔器处管柱的轴向力不断增大。同时,由于管柱自重和上部悬挂约束作用加大,中和点以上管柱处于受拉状态,结构稳定,不会发生屈曲变形;反之,中和点以下至封隔器的管柱处于受压状态,管柱易发生屈曲变形[10]。如果井筒内持续动态载荷诱发管柱振动,屈曲变形的管柱将与套管壁发生碰撞接触,产生接触压力,加剧管柱的变形失效[12]。为了获得动态载荷作用对UGS管柱受力变形的影响,考虑UGS井身结构和井下工具分布较为复杂,做出如下假设:①井下管柱为长直杆件,并且是各向同性、均匀连续的线弹性体;②忽略管柱上提或下放过程中的瞬态影响;③忽略接头等部件对屈曲的影响。
2 慢动力法载荷设置
慢动力法是采用瞬态动力分析方法解决静力学问题的一种方法[14]。其本质是利用动力学方法,对目标结构在计算周期内逐步施加外载荷,将静力学问题转化为动力响应的求解过程。考虑UGS注采生产中高速气流的不稳定性因素, UGS管柱受力一定范围内存在压力波动,即真实载荷存在一定波动范围。因此,为接近真实工况,在管柱屈曲行为分析时,通过慢动力法添加正弦波式外载荷,其中受压管段扭矩FM(t)和横向扰动力FR(t)的计算公式分别为[15]:
(1)
(2)
式中:q为管柱的单位长度重力,N/m;T为管柱固有周期,s;FR为初始扰动力,N。
为弥补管柱屈曲初始条件的不足,并提高计算效率和计算精度,在t
(3)
(4)
(5)
Ft,b=qhLsin(2πt/T)
(6)
式中:Ft,b为初始悬挂拉力,N;hL为管柱受拉段长度,m;E为油管弹性模量,MPa;I为油管截面惯性矩,m4。
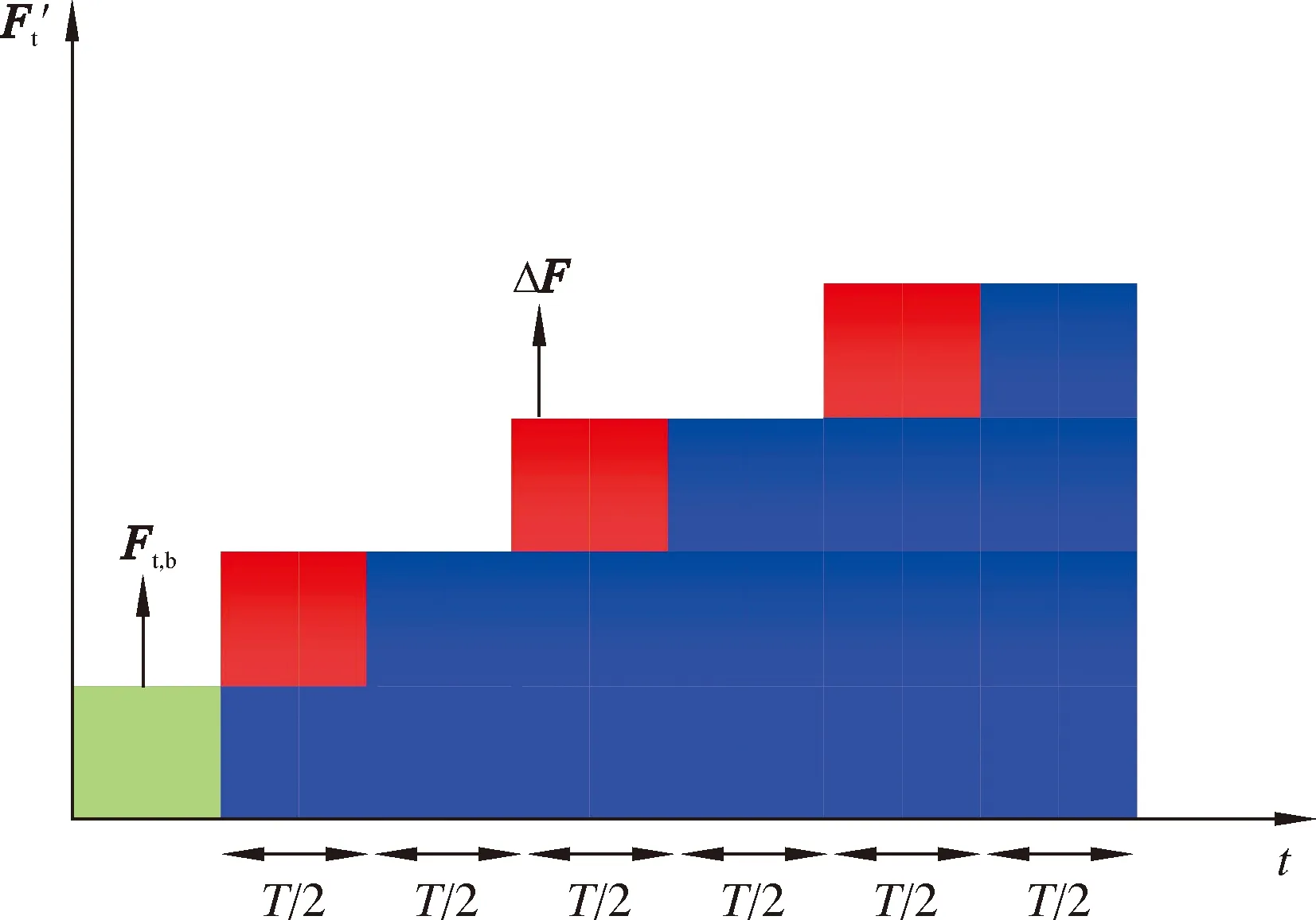
图2 阶跃式载荷的设置Fig.2 Setting of step type load
3 考虑接触的管柱屈曲动力学方程
考虑接触的管柱屈曲动力学方程为[10,15]:
(7)
C=αM=4πw1ζM
(8)
式中:M为质量矩阵;C为阻尼矩阵;K0为线弹性刚度矩阵;Kσ(d)、Kn(d)分别为管柱的几何、接触刚度矩阵;d为管柱振动时节点的位移;F(t)为关注的节点载荷向量;t为计算时间,s;w1为管柱固有频率,Hz;ζ为阻尼比。
应用UGS非线性振动分析方法[15]求解获得t时刻的振动频域值,代入式(7)中并通过Newmark 直接积分法进行隐式求解。在求解过程中,施加随计算时间延长的阶跃式外载荷,可通过管柱挠度变化来判断管柱的屈曲演变过程,当任一位置管柱挠度不再随时间变化时,则管柱处于屈曲临界状态,从而获得管柱屈曲演变构型及临界载荷。
4 现场实例分析
某衰竭油气藏储气库ZY区块井群位于华南地域,由原主力生产井改建而成。UGS-ZY区块储气库建成后,用以满足目前陕京线、陕京二线和西气东输等长输管线对储气库季节及安全调峰气量的迫切需求[16],因此,对储气库群设计和安全运行要求比较高。该区块井群储层以成层分布的溶蚀孔洞为主,岩性致密,有效厚度为6.16~10.52 m,具有天然良好的密封构造。井群深度2 400~3 900 m,地温梯度0.031 ℃/m,地层压力30.4 MPa,储层孔隙度范围6.4%~8.7%。本文主要针对UGS-ZY11井进行分析,现场基本井况参数为:油管规格ø114.3 mm×14.22 mm,套管规格ø177.8×10.36 mm,下深3 674 m,设计库容量(5.0~10.4)×108m3,运行压力10~40 MPa,工作气量(5~8)×108m3。
4.1 慢动力法UGS管柱屈曲演变分析
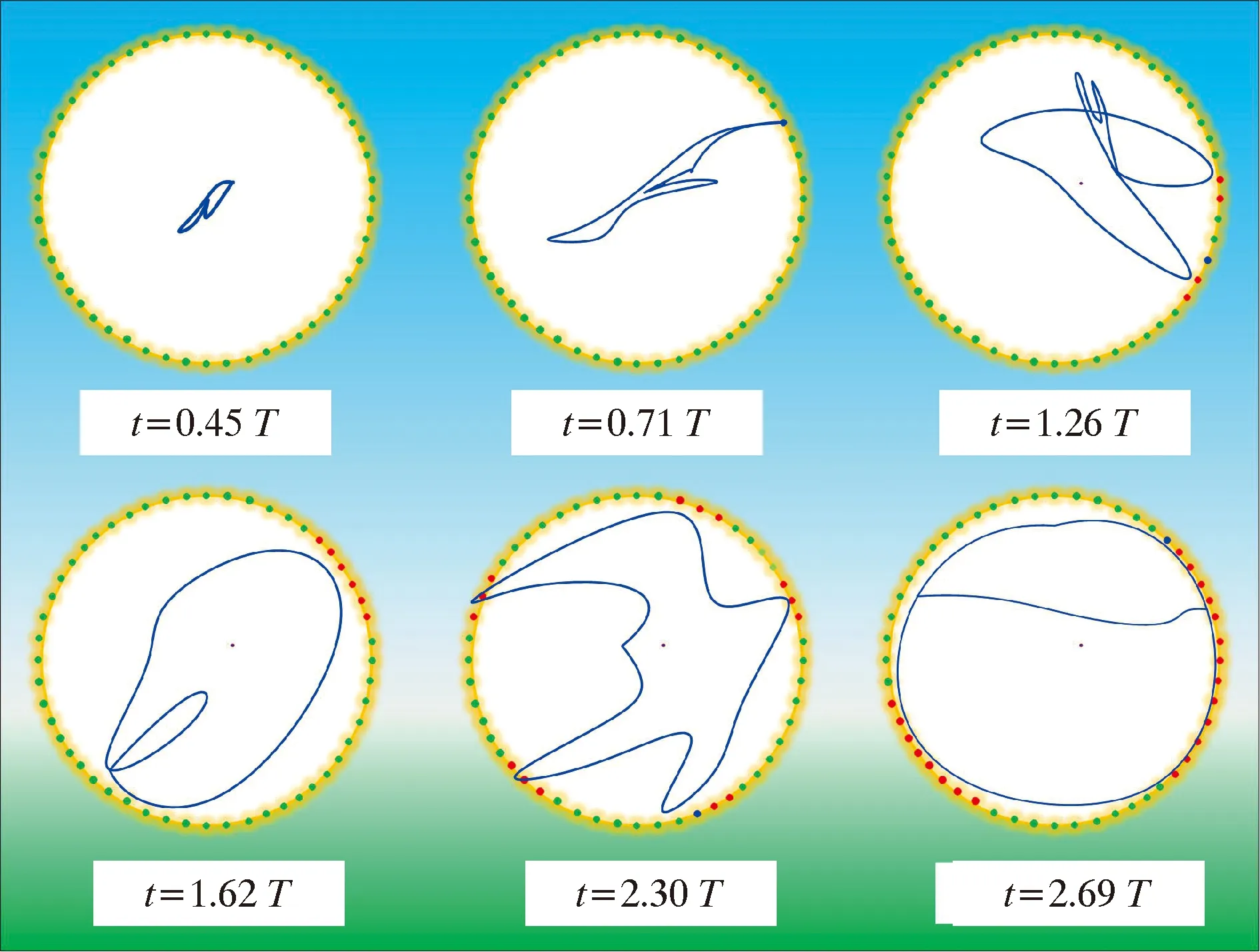
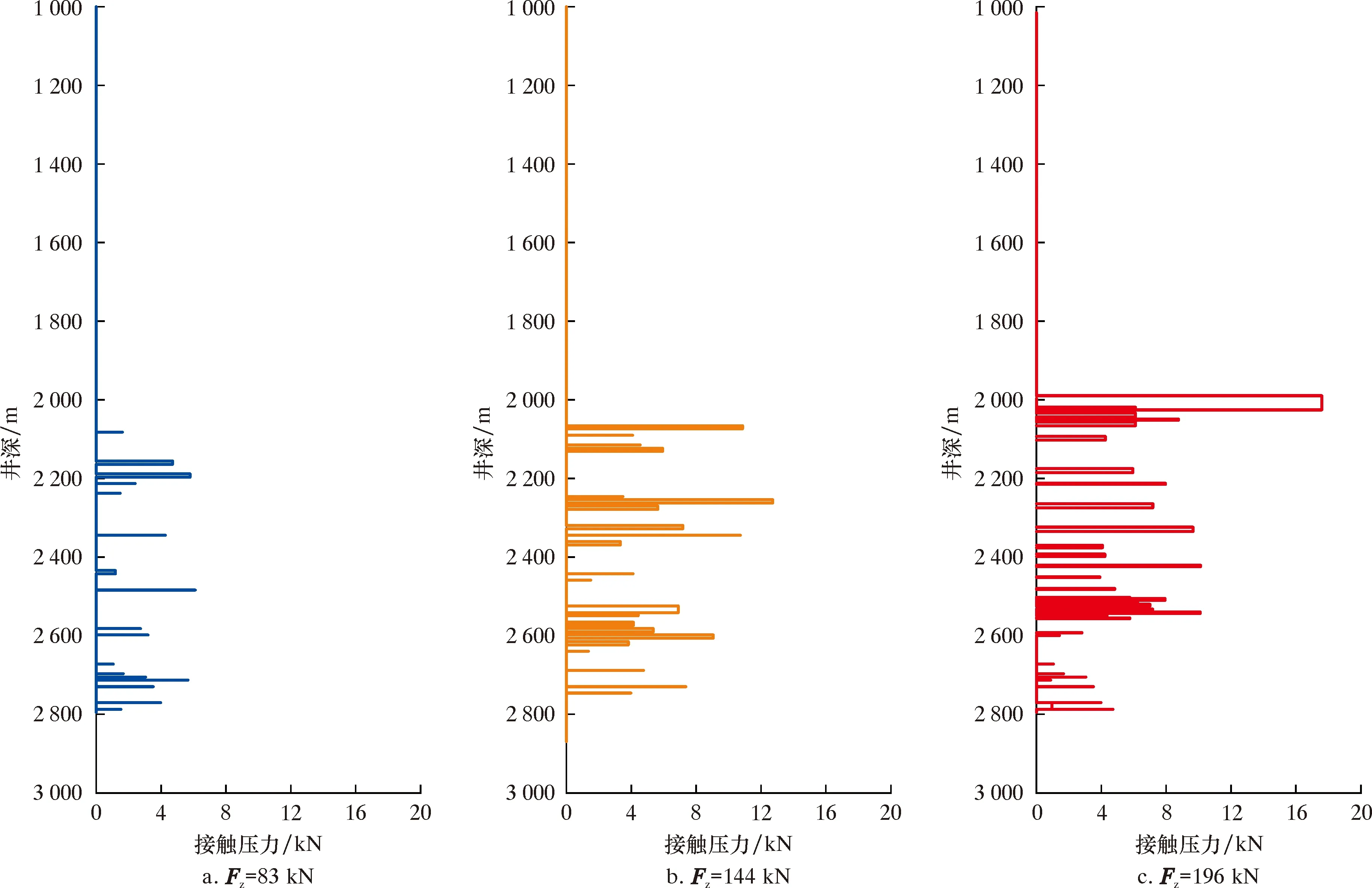
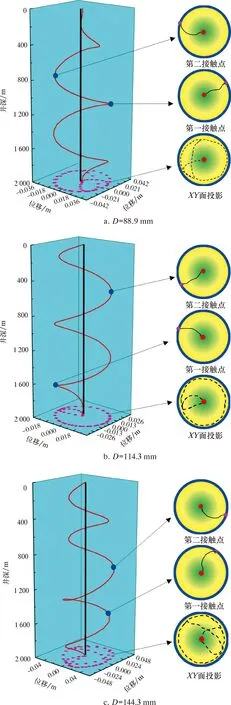
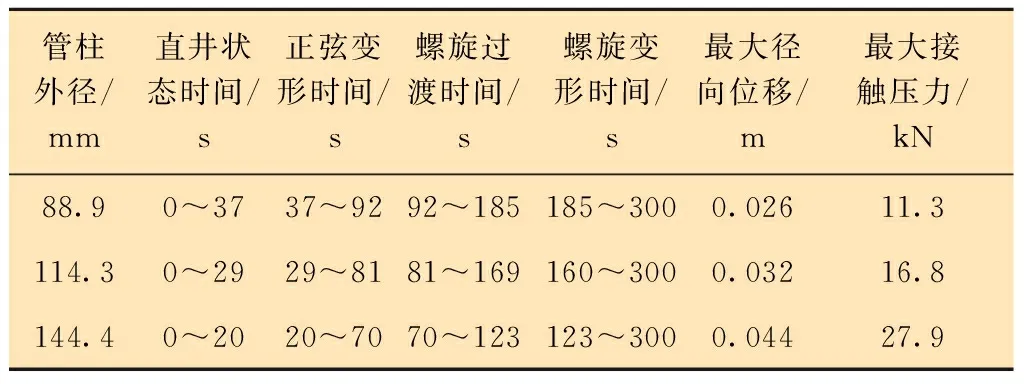
以UGS-ZY11井现场工况为例,采用慢动力法对管柱屈曲演变进行分析[17-18]。提取分析过程中管柱受压段AB位置的横向挠度(u和v)和油套环空空隙r。图3为运算周期(3T)内管柱受压段A、B位置挠度u/r和v/r的变化曲线,提取的A、B位置横向挠度值反映了管柱进入螺旋屈曲至稳定期间的变化趋势。由图 3 可知,运算周期(3T)内,在T/4 图4所示为动态载荷作用下管柱三维屈曲构型变化图。由图4可知,随着施加的阶跃式载荷的增长,管柱逐渐由直线状态进入正弦弯曲状态,最终进入螺旋弯曲状态。随着计算周期的增加,油管的径向变形从井底逐渐向上发展,最后可形成全井的变形。其中,当t≤T/2 时,在初始扰动载荷作用下,屈曲构型随着时间的延长开始变化; 当T/2 图3 运算周期(3T)内管柱受压段A、B位置横向挠度的变化曲线Fig.3 Transverse deflection variation curve of positions A and B in pressure bearing interval of the string within computing period (3T) 图4 动态载荷作用下管柱三维屈曲构型变化图Fig.4 3D buckling configuration variation of string under dynamic loads 图5表示以管柱简化为质点,管柱屈曲构型演变的过程。由图5可以看出:当t<0. 71T时, 管柱与套管壁未产生接触; 当t=0.71T时,管柱与套管壁产生一个接触点,对应临界载荷为83 kN;当 1.26T 图5 管柱屈曲构型演变Fig.5 Buckling configuration evolution of string 为验证慢动力法求解管柱屈曲结果的准确性,本文利用ABAQUS对同一生产工况的UGS管柱屈曲进行有限元分析。设定管柱为实体单元,套管视为刚体,不考虑其变形分析[19-21],结合现场数据设定模型所处基本工况为:环空带压(井口0、井底18 MPa),管柱内压(井口25 MPa、井底50 MPa),切向摩擦因数0.2。为提高计算效率,基于UGS管柱屈曲演变分析结果提取管柱受力变形的轴向力临界载荷Fz(83、112、144和196 kN)进行分析,图6为管柱轴向力随井深的变化关系图。由图6可知,底部管柱始终处于受压状态,并随着底部载荷的增加,管柱中和点上移。 图7为管柱轴向屈曲形态的数值模拟结果。由图7可知,随着轴向受力的增大,油管从直线状态逐渐进入正弦弯曲状态,最终进入螺旋弯曲状态。油管的径向变形也从井底逐渐向上发展,最后形成全井的变形,结果表明管柱的变形弯曲状态主要由管柱轴向力决定。例如,当底部管柱轴向力小于临界载荷值83 kN时,管柱轴向尚未发生变形,呈直线状态;当底部管柱轴向力从83 kN逐渐增大到112 kN时,管柱由直线状态逐渐变为正弦弯曲状态,管柱沿径向开始产生位移(见图7c),但未与管壁接触,主要原因是环空压力对管柱与套管壁接触存在“软约束”。当下端的轴向力从151 kN逐渐增大到196 kN时,管柱由正弦弯曲状态向螺旋弯曲状态过渡, 其径向方向产生的位移持续增大,与套管壁的接触位置和范围也增加。研究结果表明慢动力法求解管柱屈曲计算结果可信。 图6 管柱轴向力随井深的变化关系图Fig.6 Axial force of string vs well depth 图8为轴向力临界载荷下(83、144和196 kN)UGS管柱屈曲变形后与套管壁的接触压力分布。由图8可知,管柱屈曲后套管壁接触位置发生在2 000~2 800 m,接触压力分布的疏密反映出管柱产生了连续非均匀的屈曲状态。随着轴向压力增大,管柱屈曲后与套管壁的接触密集程度明显增加,对应的接触压力分布也密集产生。接触压力最大值主要分布在接触部位的顶部,其中临界载荷为83、144和196 kN 时,对应的接触压力最大值分别为6.5、13.7和18.3 kN。同时,2 300~25 00 m部分的管柱-套管壁接触稀疏,表明该区域管柱屈曲变形出现自锁现象,导致其接触压力较小,此时已进入永久屈曲状态。若永久屈曲的管柱发生振动,其与套管壁易产生接触摩擦力,将加剧油套管损伤破坏。 4.3.1 不同管径 基于动态载荷的UGS管柱非线性屈曲构型演变分析,利用有限元软件ABAQUS进一步研究了生产过程管柱管径和储气库产量等对UGS管柱屈曲变形的影响。图9和表1为不同管柱管径D(88.9、114.3和144.3 mm)对管柱非线性屈曲的分析结果。由表1可知,同一生产工况下,不同管径管柱处于直井状态的时间分别为37、29和20 s,处于正弦弯曲状态的时间分别为55、52和50 s, 图7 管柱轴向屈曲形态的数值模拟结果Fig.7 Numerical simulation results of axial buckling shape of string 图8 临界载荷下管柱屈曲变形后与套管壁的接触压力分布Fig.8 Distribution of contact pressure between string and casing wall after buckling deformation of string under critical load 图9 不同管径对UGS管柱屈曲的影响Fig.9 Effect of different pipe diameters on buckling of UGS string 处于过渡状态的时间分别为93、88和53 s。由此可知,管径越大,管柱处于直线状态、正弦弯曲状态和过渡状态的时间越短,管柱越容易发生螺旋变形。 同时,生产所用油管柱的管径越大,达到临界载荷发生屈曲的管柱径向位移越大,对应的管柱(88.9、114.3和144.3 mm)径向最大位移分别为0.026、0.032和0.044 m,管柱与套管的最大接触压力分别为11.3、16.8和27.9 kN。由管柱与套管壁的第一、第二接触点位置可知,随着管径的增大,屈曲变形管段与套管壁第一接触点的位置下移,说明油管的内径越大,发生变形碰撞后其接触压力就越大。 表1 不同管径下管柱屈曲分析结果Table 1 String buckling analysis results under different pipe diameters 4.3.2 不同注采量 同一生产工况下(油管规格ø114.3 mm×14.22 mm,套管规格ø177.8 mm×10.36 mm),模拟分析不同注采量Q(9.2×104、17.9×104和 26.6×104m3/d)对管柱非线性屈曲变形的影响规律,结果如表2和图10所示。由表2和图10可知,不同注采量下,管柱处于直井状态的时间分别为26、22和17 s,处于正弦弯曲状态的时间分别为62、49和40 s,处于过渡状态的时间分别为72、61和35 s。由此可知,随着注采量的增加,管柱更容易发生屈曲变形。 同时,随着UGS注采量的增加,达到临界载荷发生屈曲的管柱径向位移越大,对应不同注采量Q(9.2×104、17.9×104和26.6×104m3/d)的径向最大位移分别为0.023、0.038和0.041 m,且在注采量为9.2×104m3/d时,管柱最大径向位移小于环空间隙情况下产生接触压力,表明动态载荷作用下诱发管柱振动,导致变形的油管柱与套管壁发生接触。同时,由管柱与套管壁的第一、第二接触点位置可知,随着UGS注采量的增大,屈曲变形管段与套管壁第一接触点的位置下移。 表2 不同注采量下管柱屈曲分析结果Table 2 String buckling analysis results under different injection-production volumes 图10 不同注采量对UGS管柱屈曲的影响规律Fig.10 Effect of different injection-production volumes on buckling of UGS string (1)根据储气库井筒结构特点建立柔性约束下储气库井管柱非线性屈曲力学模型,以UGS-ZY11井现场数据为例,引入慢动力法和考虑接触的管柱屈曲动力学方程,分析动态载荷作用下管柱的非线性屈曲过程和临界载荷,并通过ABAQUS模拟计算进行对比研究,结果表明动态载荷作用下管柱中和点到封隔器处的管柱处于连续非均匀的屈曲构型。 (2)对UGS管柱进行动态载荷下管柱屈曲有限元分析,证实管柱的变形弯曲状态主要由管柱轴向力决定。随着轴向力的增大,油管从直线状态逐渐进入正弦弯曲状态,最终进入螺旋弯曲状态。同时,在管柱受力变形初始阶段,环空压力对其与套管壁接触存在“软约束”。随着储气库井产量和管径的增加,管柱屈曲变形过渡的时间越短,管柱越容易发生螺旋变形。 (3)动态载荷作用下诱发管柱振动,导致径向位移较小的油管柱与套管壁发生接触,表明管柱振动将加剧油套管损伤失效破坏,在管柱安全生产设计和运行时应做出相应的安全措施。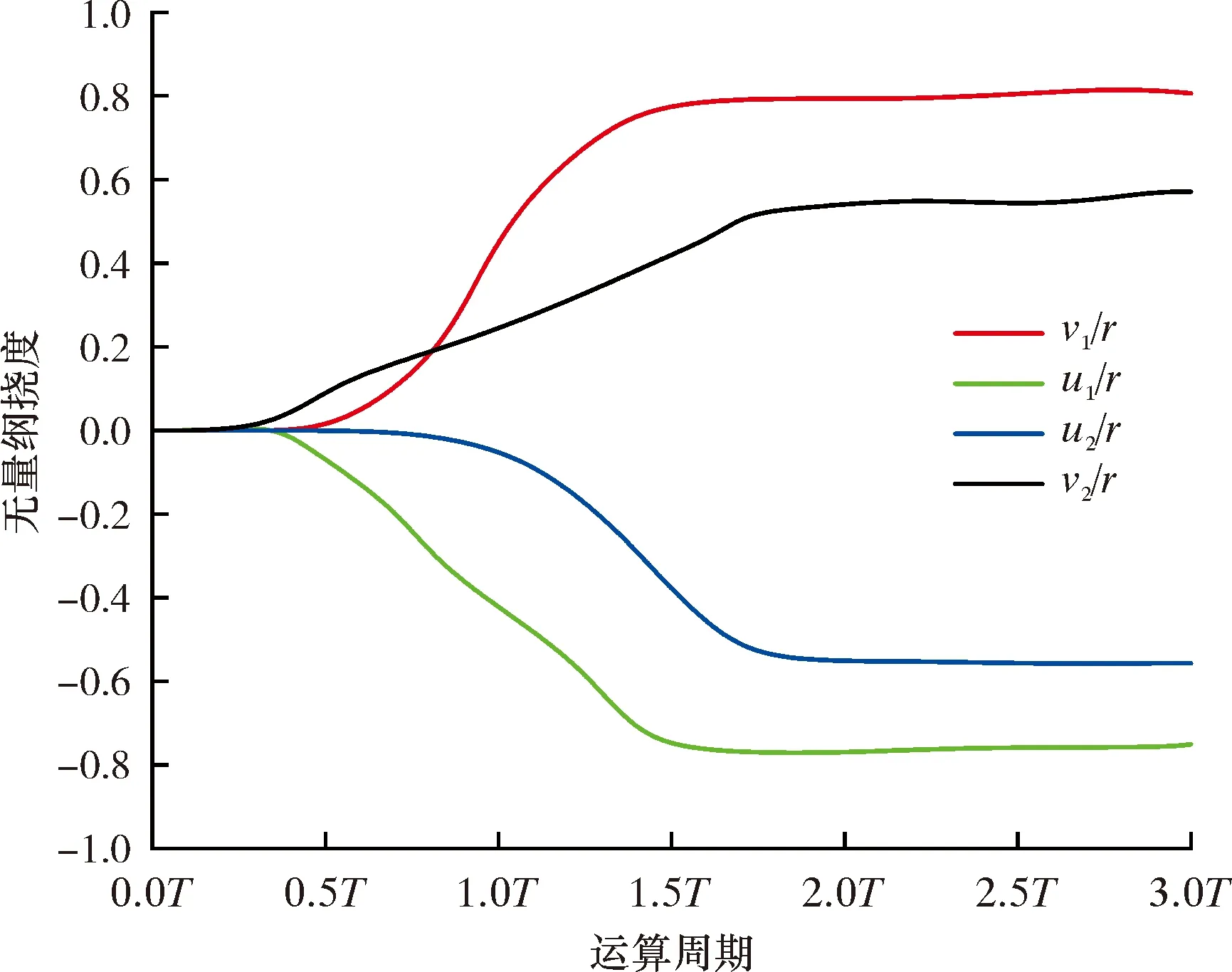

4.2 动态载荷下UGS管柱屈曲有限元分析

4.3 影响因素分析



5 结 论
