基于AMESim的节流阀自动控制系统*
2021-04-23张锐尧李军柳贡慧明瑞卿岳婷
张锐尧 李军,2 柳贡慧,3 明瑞卿 岳婷
(1.中国石油大学(北京)石油工程学院 2. 中国石油大学(北京)克拉玛依校区3.北京工业大学 4.中国石油勘探开发研究院 5.中国石油大学(北京)经济管理学院)
0 引 言
随着我国经济的不断发展,对油气资源的需求量也日益增加,其中大部分是依赖于进口,对外依存度达到70%[1-3],因此亟需加大国内油气勘探开发力度,从而减少油气的对外依存度[4]。随着我国浅部地层优质油气资源的持续开采,深水油气将是我国油气勘探开发的重要接替区[5-6]。但是深水区地层环境复杂,浅层存在弱胶结、易坍塌以及孔隙压力高、破裂压力低等问题。特别是南海北部莺琼盆地有超过75%的地区高温高压地层发育,地层压力系数近2.3,压力窗口狭窄[7],极易发生溢流、气侵或漏失等,从而造成极大的资源浪费、设备损坏、环境污染、甚至人员伤亡等[8-9]。因此,在控压钻井过程中经常需要通过压井作业来实现安全钻进,而其中的关键环节就是通过调节节流阀的开度来实现对回压的控制,最终实现对井底压力的调节[10],从而避免井下复杂情况的发生。然而现有的节流阀控制系统需要人工操作,而人工操作控制精度低,且具有盲目性与主观性[11],如果出现操作不当,不但解决不了问题,而且还会使得井下情况进一步恶化,最终造成重大的损失[12]。所以针对该技术问题,有必要研究一套自动化程度高且性能稳定的节流阀自动控制系统。本文首先介绍了节流阀自动控制系统的结构与工作原理,然后对系统各部分进行了设计,并得到了系统的传递函数,然后根据传递函数模型进行分析。AMESim软件可以在统一的平台上实现多学科领域的系统工程的建模和仿真,并且其智能求解器的鲁棒性极强,因此本文利用AMESim软件建立了自动控制系统的仿真物理模型,最后对仿真结果进行了分析。
1 节流阀自动控制系统的工作原理
节流阀自动控制系统工作原理示意图如图1所示。节流阀自动控制系统主要包括输入信号源、PID控制器、比例放大器、电液比例阀、液压缸、位移传感器和楔形节流阀等,其中液压缸的活塞-活塞杆执行机构与节流阀的阀芯连接。在钻井作业中,如果出现溢流或气侵等井下复杂情况时,钻井现场的PAC控制系统会将收集的信号源传递给比例放大器,实现对信号放大处理。该信号会与节流阀的反馈位移信号进行误差分析,当误差信号经过PID控制器处理后,会再传递给电液比例阀,从而实现对电液比例阀油路的切换。而电液比例阀的两个压力出口分别与液压缸的有杆腔和无杆腔相连,从而可实现液压缸的活塞-活塞杆执行结构的往复运动。又因为该执行机构与节流阀的阀芯直接相连,最终可以实现对节流阀开度的自动调节。综上所述,得到了节流阀开度的自动调节及其位移信号实时反馈的闭环控制系统。

图1 节流阀自动控制系统工作原理示意图Fig.1 Working principle of automatic throttle control system
2 节流阀自动控制系统的设计
根据节流阀自动控制系统的工作原理,输入信号源需要在系统各子元件之间传递才能实现节流阀开度的自动控制与调节,而信号的传递都是通过传递函数来实现[13]。本文一方面先对比例放大器、电液比例阀和位移传感器进行选型,从而确定各自的传递函数数学模型;另一方面,又因为节流阀的开度调节先通过电液比例阀换向,改变液压缸腔内液压油的流动方向,从而实现液压缸执行机构的往复运动,而液压缸的执行机构与节流阀相连,进一步地实现了节流阀的开度调节,所以整个液压系统的传递函数又可以分为两个部分,即以电液比例阀的位移为输入、液压缸的位移为输出,以及以节流阀的负载为输入、液压缸的位移为输出。通过叠加原理就可以得到整个系统的传递函数的数学模型。
2.1 系统各子元件的传递函数模型
根据比例放大器、电液比例阀以及位移传感器的选型以及工作特性[14-15],可以分别得到各自的传递函数:
(1)
式中:I(s)为比例放大器输出电流,取值2 A;U(s)为数字控制器输出经转换成的模拟电压信号,取值10 V;Ka为比例放大器增益,A/V;η为阻尼比,一般为0.5~0.7;f为频率,取值87 rad/s;Kv为比例系数,取值0.6×10-3;δ为传感器增益,V/m;Ypod为活塞执行结构的位移,取值0.06 m;Uc为反馈电压,取值5 V。
2.2 液压控制系统的传递函数模型
图2为液压系统工作原理示意图。由图2可知:当电液比例阀的右侧线圈通电时,则左侧液路为通路,液压油由阀的中路进入后会进入到液压缸的左侧腔内,从而推动活塞-活塞杆执行机构向右运动,节流阀的开度则变小;反之,如果电液比例阀的另一侧通电,则可以实现节流阀开度的反方向调节。因此,基于电液比例阀以及液压缸的负载-流量特性方程,就可以建立电液比例阀与液压缸以及液压缸与节流阀之间的传递函数。

图2 液压系统工作原理示意图Fig.2 Working principle of hydraulic system
2.2.1 电液比例阀的负载-流量方程
由电液比例阀的特性可以得到其入口与出口流量方程[16]:
(2)
然后根据电液比例阀的进出口质量守恒关系以及节流阀与液压缸的执行结构之间力的平衡关系,即有:
(3)
由于本文选择的电液比例阀为零开口四通滑阀,所以可以得到其负载流量为进出口流量之和的[17-18],故可以分别得到节流阀正向移动与负向移动时的负载流量方程:
(4)
将式(4)中的流量方程进行统一和线性化处理,得到如式(5)所示的负载流量方程:
Qv=δQLv-δppv
(5)
其中:
(6)
(7)
式中:CQ为电液比例阀节流口流量系数,取0.5;ΔA为电液比例阀节流窗口面积梯度,m2;Qin为电液比例阀入口流量,m3/s;Lv为阀芯位移,m;ρ为液压油密度,kg/m3;pL为节流阀动力机构活塞左侧压力,MPa;ps为系统输入压力,MPa;p0为系统输出压力,MPa;pR为节流阀动力机构活塞右侧压力,MPa;pv为负载压降,MPa ;Qin为电液比例阀入口流量,m3/s;Qout为电液比例阀出口流量,m3/s;Qv为电液比例阀负载流量,m3/s;δQ为电液比例阀稳定工作时的流量增益,m2/s;δp为电液比例阀稳定工作时压力流量系数,m5/(N·s)。
2.2.2 液压缸的压力-流量特性方程
基于液压缸的工作特性,并结合连续性方程,可得到如式(8)所示的液压缸进油腔方程、如式(9)所示的回油腔方程以及如式(10)所示的液压缸容积的变化量。
(8)
(9)
(10)

(11)

(12)
(13)
对上述式(5)、式(11)和式(13)进行拉普拉斯变换,可以得到如式(14)~式(16)所示的方程:
Qv(s)=δQLv(s)-δPpv(s)
(14)
Qv(s)=AsY+[Cic+Cec/2+Vs/(4βe)]pv
(15)
pv(s)=[(ms2+ζs+K)Y(s)+Fd]/A
(16)
式中:Cic为液压缸内泄漏系数;Cec为液压缸外泄漏系数;VL为液压缸进油腔容积,m3;VR为液压缸回油腔容积,m3;m为执行机构的总质量,kg;ζ为黏性阻尼系数;K为弹簧刚度,N/m;Fd为钻井液对节流阀阀芯的作用力,N;Fp为液压油作用力,N;A为液压油预作用于活塞的有效面积,m2;Y(s)为液压缸的位移,m。
根据式(14)~式(16),并由位移叠加原理,同时由于执行机构为无弹性负载且泄漏产生的阻尼系数A2/(δQ+Cic+Cec) 要远大于常规阻尼系数ζ[19],所以对上述两式进行简化后可以得到系统总的传递函数:
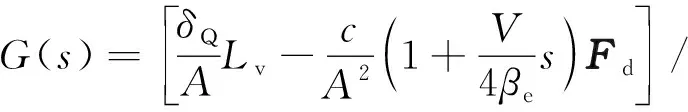
(17)
其中:
(18)
(19)
(20)
2.3 节流阀开度与压降数学模型
图3所示为节流阀运动过程中最小过流面积的变化情况。由图3可知,当楔形节流阀从左向右运动时,节流阀的开度从100%到0%变化。由于节流阀在运动过程中,其最小过流面积为动态变化的弧形面积,所以在不影响计算精度的条件下假设弧形面积为其外接矩形面积。若节流阀在任意时刻的行程为hi,初始状态时节流阀全部开启,则行程为0;若完全关闭时的行程为L,则节流阀的开度与行程的关系如式(21)所示。若不考虑节流阀结构的影响,则可以得到楔形节流阀的流量方程,如式(22)所示,并进一步整理得到节流阀压降的计算公式,如式(23)所示。
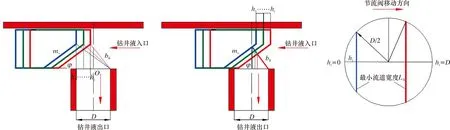
图3 节流阀运动过程中最小过流面积的变化情况Fig.3 Change in minimum open area in the process of throttle movement
δ=1-(L-hi)×100%/L
(21)
(22)
(23)
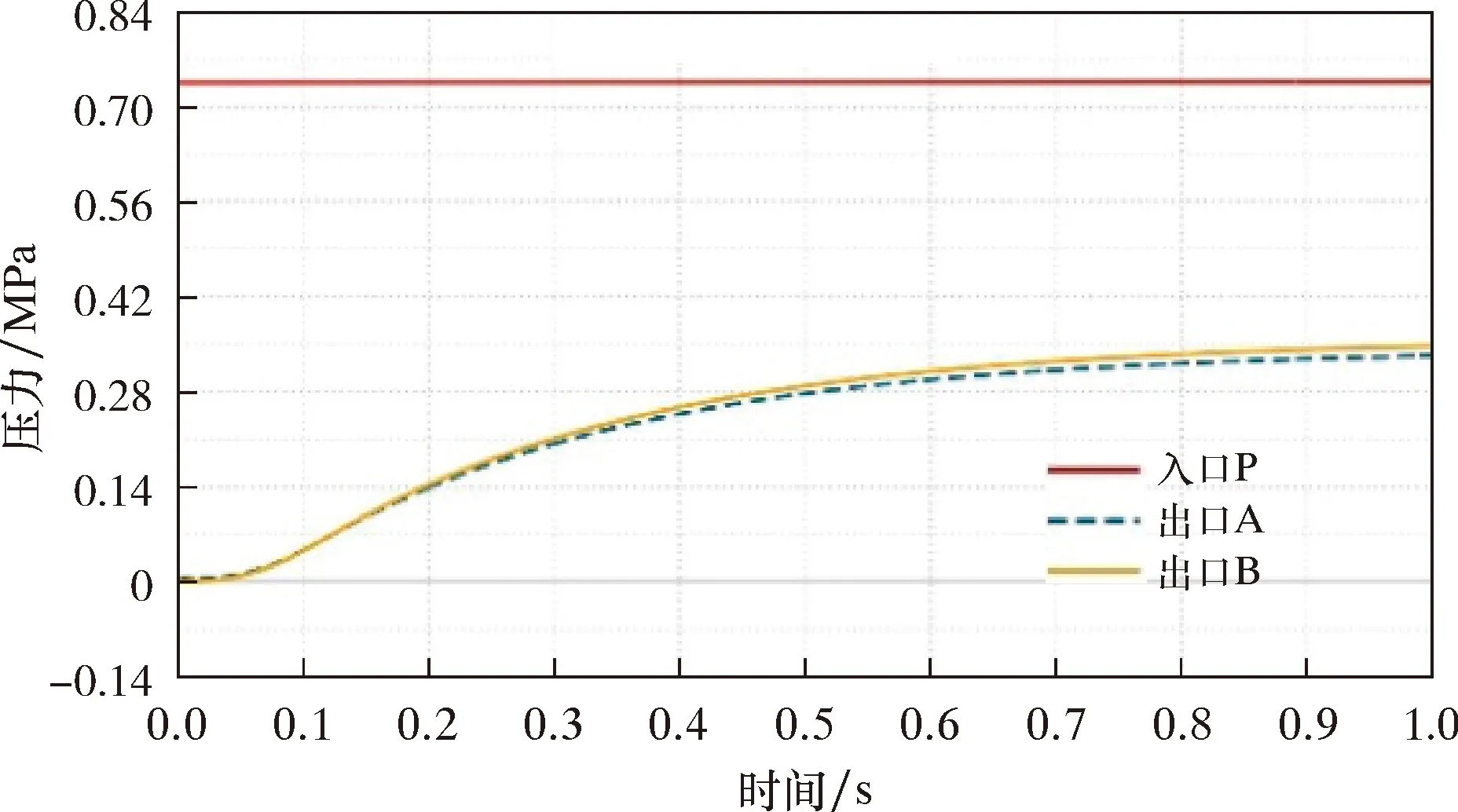
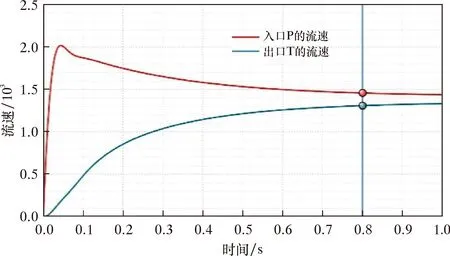
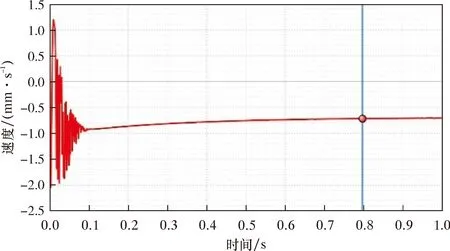
初始状态时,节流阀全部开启,则最小过流面积等于钻井液出口面积,即Af=π(D/2)2;若节流阀在钻井液出口的中轴线左侧时,即0 (24) (25) 结合式(23)~式(25)可以得到节流阀的压降与位移的关系,如式(26)所示,并将相关数据带入可以得到节流阀的压降与节流速度随节流阀开度的变化规律,如图4所示。 (26) 式中:δ为节流阀的开度,%;hi为节流阀的位移,mm;A为阀座中流道的面积,mm2;Af为钻井液在节流阀中的最小过流面积,mm2;Δp为节流阀进出口压降,MPa;Q为流量,m3/s;ρ为钻井液密度,kg/m3;mv为节流阀斜边长度,mm;D为钻井液的出口直径,mm。 图4 节流阀压降与节流速度随开度的变化规律Fig.4 Variation of throttle pressure drawdown and throttling velocity with opening 基于该传递函数,并结合各控制元件的连接与布置方式,利用AMESim软件建立了节流阀自动控制系统的仿真系统物理模型,如图7所示。信号输入后,通过增益实现信号放大,并与节流阀的反馈位移之间进行误差计算,然后位移误差信号通过PID控制器进行处理后变为控制信号,经过放大后传递给电液比例阀,从而实现电液比例阀液路的切换。进一步实现液压缸有杆腔与无杆腔压力的变化,使得活塞-活塞杆执行机构做往复直线运动。而节流阀又与活塞杆直接连接,所以在执行机构的往复运动过程中就实现了节流阀开度的自动控制与调节。 图5 传递函数框图Fig.5 Block diagram of transfer function 图6 控制系统传递函数的伯德图Fig.6 Bode diagram for transfer function of control system 根据图7所示的节流阀自动控制系统进行仿真,得到的仿真结果如图8~图17所示。其中图8~图10为系统运行时电液比例阀的性能指标随时间的变化情况。从图8可以看出,当系统刚启动时,电液比例阀的入口P处的流量在0.1 s内快速增加,而出口A和B的流量逐渐减小。当系统运行0.8 s后,流量基本趋于稳定状态。由图9可知,电液比例阀的入口压力值保持恒定,而出口A和B的压力值随着运行时间的延长而增加,当运行1.0 s后,出口压力也达到恒定状态。图10所示为分数阀芯位移与速度随系统运行时间的变化。由图10可知,随着时间的延长,分数阀芯位移快速增加,而分数阀芯速度则快速减小,当系统运行0.12 s时,两者都达到稳定值。从图11可以看出,电液比例阀的入口P和出口T的流速同样在系统运行0.8 s后达到了稳定的状态。 图7 节流阀自动控制系统的仿真系统Fig.7 Simulation system of automatic throttle control system 图8 电液比例阀出、入口流量的变化Fig.8 Change in flow rate at inlet and outlet of electro-hydraulic proportional valve 图9 电液比例阀出、入口压力的变化Fig.9 Change in pressure at inlet and outlet of electro-hydraulic proportional valve 图10 电液比例阀的分数阀芯位移与速度的变化Fig.10 Displacement and speed variation of fractional spool of electro-hydraulic proportional valve 图11 电液比例阀出、入口流速的变化Fig.11 Change in flow velocity at inlet and outlet of electro-hydraulic proportional valve 图12~图15所示为系统运行1.0 s后,液压缸的相关性能指标随时间的变化。其中图12为节流阀施加在活塞杆上的受力随时间的变化。在系统刚启动时,活塞杆的受力存在一定的波动。当系统运行0.1 s后,其受力的波动幅度逐渐减小,并在0.1 s后达到了稳定状态。由图13和图14可知:在系统运行0.1 s后,无杆腔的流量快速增加,导致其压力逐渐增加,从而推动执行机构向右运动;有杆腔的流量逐渐减小,由于其体积不断减小,所以压力也逐渐增加。但是执行机构在压差作用下从左往右运动,在运行1.0 s后液压缸的运行也达到了稳定状态。又因为系统刚启动0.1 s,活塞杆的受力存在一定的波动,所以其运动速度也不稳定,当运行0.8 s后其运动速度趋于稳定,如图15所示。 同理,由图16~图17可知,因为节流阀与活塞杆直接相连,所以其受力与活塞杆相同,在系统运行0.10 s内,节流阀的受力及加速度都存在较大幅度的波动。当运行0.12 s后其受力与加速度都达到了恒定状态。而其速度在0.8 s时开始趋于稳定,所以其位移随着时间的延长也呈线性增加。 综上所述,在控制系统运行1.0 s后,通过对关键控制元件进行仿真分析,系统中电液比例阀、液压缸以及节流阀的性能参数都在0.1~1.0 s内达到了稳定状态,说明该节流阀自动控制系统具有较好的稳定性和快速性。 图12 液压缸的活塞杆受力的变化Fig.12 Change in force on piston rod of hydraulic cylinder 图13 液压缸内流量的变化Fig.13 Change in flow rate within hydraulic cylinder 图14 液压缸内压力的变化Fig.14 Change in pressure within hydraulic cylinder 图15 活塞杆运动速度的变化 Fig.15 Change in piston rod movement velocity 图16 节流阀位移与关闭速度随时间的变化Fig.16 Variation of throttle displacement and closing velocity with time 图17 节流阀加速度与受力随时间的变化Fig.17 Variation of acceleration and stress of throttle with time 通过对节流阀自动控制系统的传递函数数学模型的推导,并以此建立了节流阀自动控制系统模型,然后对仿真结果进行了稳定性分析,同时,还分析了节流压降与速度随节流阀开度的变化规律。基于以上研究得出如下结论: (1)所推导的节流阀自动控制系统的传递函数数学模型可以为压井作业中节流阀开度的自动、精准调节提供理论依据,从而提升压井作业的安全性、准确性与高效性。 (2)建立了节流阀自动控制系统模型,通过仿真结果分析,系统具有较好的稳定性与快速性,符合工程控制技术的要求。 (3) 由节流阀开度与节流阀压降之间的数学关系计算可知,随着节流阀开度的不断增加,钻井液有效过流面积逐渐增加,所以其节流压降与速度都逐渐减小。该研究可以有效确定节流阀的压降随节流阀位置的变化情况,为压井作业中井底压力的准确调节提供了技术支撑。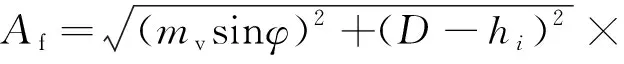

3 节流阀自动控制系统的建立与仿真分析
3.1 节流阀自动控制系统的建立
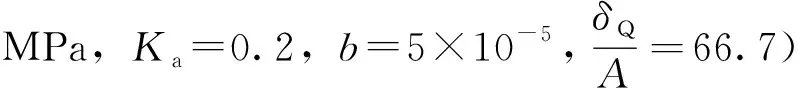


3.2 仿真结果分析








4 结 论
