基于分区法的扩眼器刀翼布齿优化研究*

张全立 曹通 侯福祥 喻开安

(1.中国石油集团工程技术研究院有限公司 2.中国石油大学(北京) 机械与储运工程学院)

0 引 言

扩眼器广泛应用于石油天然气钻井作业中[1-6]，用以解决井眼缩径、优化套管程序以及提高固井质量等各种井下复杂工况作业问题。在扩眼器破岩过程中，刀翼受力不均会产生不平衡侧向力，导致扩眼器发生横向振动，并在井眼轴向方向上产生“小台阶”，影响井眼质量；并且长时间振动容易引起钻具提前疲劳失效，影响钻井作业安全。因此，为了提高扩眼质量和保证作业安全，有必要对扩眼器刀翼布齿进行优化，从而尽可能地减小扩眼过程中的侧向力。扩眼器和PDC钻头的破岩过程在本质上相同，都是固定切削齿绕着钻具中心线旋转切削岩石，因此可以将PDC钻头布齿优化理论应用于扩眼器[7-8]。

邹德永等[9-10]通过切削齿在不同情况下的切削试验，研究了切削参数、钻头参数及岩石性质等对PDC钻头受力的影响，建立了PDC钻头受力的数学计算模型，提出了切削参数的方程计算法，建立了侧向力的计算方程，并给出了以刀翼周向角为变量的布齿优化方法。宋洵成等[11]利用遗传算法建立了PDC钻头侧向力平衡优化设计方法，解决了散布式钻头相比刀翼式钻头优化数目增多而导致的计算量大幅增加的问题。李辉等[12]采用融合了蚁群算法和粒子群算法(PSO)的混合算法对PDC钻头侧向力进行优化，充分利用了PSO算法的快速、全局收敛性和蚁群算法的正反馈机制，与单独采用PSO优化算法的结果相比，优化结果更好，收敛速度更快。马亚超等[13-14]提出了磨损状态下PDC钻头切削齿切削参数的计算方法，建立了考虑切削齿磨损状态的PDC钻头侧向力优化模型，并利用克里金(Kriging)插值法和粒子群算法进行了算例分析，优化结果表明侧向力可大幅度减小。

现有布齿优化研究假设刀翼切削过程中受力保持恒定，只考虑了一种切削受力情况，忽略了切削过程中其他不同情况，因此优化结果的准确性有限，与实际情况的契合度较低。

本文在前人研究的基础上，提出了新的切削过程分析法——分区法：认为刀翼的切削过程可以分为几个不同的切削阶段，不同的切削阶段对应不同的切削参数和受力情况，对不同切削阶段依次进行研究，可以实现更加准确的扩眼器切削受力分析。基于分区法，建立了以各个切削阶段侧向力最小为目标，以所有切削齿后倾角为优化变量的多目标优化模型，并利用非支配排序遗传算法2(NSGA-Ⅱ)和模糊综合评价法实现了最优解的求解和选取。最后，以三刀翼扩眼器为例进行了布齿优化设计。优化结果证明，基于分区法的布齿优化设计可以大幅减小各个切削阶段的侧向力，实现扩眼器的全阶段侧向力平衡。

1 分区法

根据三刀翼扩眼器的刀翼位置，井底岩石被划分为3个不同区块。在破岩过程中的某一时刻，被切削岩石区块和切削刀翼是一一对应的切削配对，此时的切削过程可划分为一个切削阶段。随着刀翼不断地旋转，当刀翼进入新的区块，此时的切削配对关系发生了改变，相对应的切削情况也发生了改变，此时切削进入了另一个阶段。以此类推，三刀翼扩眼器旋转切削一圈的过程可以分为3个切削阶段，如图1所示。图1中虚线为已经经过的刀翼。每个切削阶段的切削情况如图2所示。

图1 扩眼器旋转切削一圈中的不同阶段Fig.1 The different stages of the reamer rotating and cutting circle

在不同的切削阶段，刀翼所切削的岩石区块不同，切削情况也不同，因此每个阶段对应不同的切削参数和受力情况。

图2 不同切削阶段的切削情况Fig.2 Cutting conditions at different cutting stages

对于n个刀翼的扩眼器，基于分区法可以将切削过程划分为n个阶段，每个阶段的切削参数计算需要依次进行，具体的计算流程如图3所示。

图3 切削参数计算流程图Fig.3 Flow chart of cutting parameter calculation

2 扩眼器布齿优化模型

基于分区法，扩眼器切削过程可以分为若干个不同的切削阶段，每个切削阶段对应不同的切削受力情况。本文以各个阶段侧向力最小为目标，以各个切削齿后倾角为优化变量，建立了布齿优化的多目标优化模型。

2.1 目标函数

借鉴PDC钻头受力的计算模型[10]，可得扩眼器侧向力计算公式：

(1)

其中：

(2)

(3)

a1=(0.03α2-0.07α+11.84)×
(2.31Kd-8.87)(0.43lnv+0.81)

(4)

b1=(0.19α2-5.34α+321.83)×
(1.10Kd-3.38)(0.04lnv+0.08)

(5)

a2=(0.01α2-1.29α+11.23)×
(2.12Kd-7.83)(0.44lnv+0.82)

(6)

b2=(0.01α2+0.03α+96.39)×
(0.31Kd-0.60)(0.04lnv+0.07)

(7)

式中：Fs为扩眼器所受总侧向力，Fx为Fs在x方向的分力，Fy为Fs在y方向的分力，n为切削齿齿数，α为切削齿后倾角，β为侧转角，γ为法向角，θc为周向角，A为切削面积，w为切削弧长，Kd为岩石可钻性级值，v为切削速度。

由扩眼器侧向力计算公式可以看出，侧向力大小与扩眼器结构参数、切削参数、地层性质及钻井参数有关，可以表示为：

Fs=f({αi,βi,γi,Ai,wi,vi,θci},Kd)
i=1,2,……,n

(8)

m刀翼扩眼器的旋转切削过程可分为m个阶段，可以得到m组不同的切削参数，代入式(8)可得到m个侧向力计算公式，如式(9)所示：

Fsj=f({αi,βi,γi,Aij,wij,vi,θci},Kd)
i=1,2,……,n；j=1,2,……,m

(9)

确定岩石性质、钻井速度、刀翼形状、切削齿的侧转角和切削齿的法向角后，当后倾角调整量较小时，可以认为切削参数保持不变，此时扩眼器的侧向力只与切削齿的后倾角有关。不同阶段的切削参数可以根据分区法进行计算，因此布齿优化的目标函数表达式可写为：

Fsj=fj({αi})
i=1,2,……,n；j=1,2,……,m

(10)

2.2 约束条件

优化中，每个切削齿的后倾角都可作为独立变量参与优化计算。同时为了保证切削齿后倾角在合理范围，优化后的后倾角需满足以下约束条件：

b1≤αi≤b2i=1,2,……,n

(11)

式中：αi为第i颗切削齿后倾角，b1、b2为边界值，需要根据实际地层情况确定。

3 齿优化模型的求解方法

3.1 基于NSGA-Ⅱ算法求解最优Pareto解集

非支配排序遗传算法2 (NSGA-Ⅱ)是Srinivas和Deb于2000年在NSGA的基础上改进的一种算法，它提出了快速非支配排序算法，降低了计算难度；采用了拥挤度和拥挤度比较算子，保持了种群的多样性；引入了精英策略，扩大了采样空间，防止了最佳个体的丢失，是目前流行的多目标优化算法之一[15-17]。在NSGA-Ⅱ中，个体的适应度体现在它的非支配排序等级和拥挤距离两个指标上，避免了目标偏好性，因而能够找出使各目标函数能尽量达到比较大(比较小)的最优解集，为多目标优化分析提供了有效的工具。本文采用NSGA-Ⅱ算法来对布齿优化模型进行求解，得到优化模型的最优Pareto解集，其具体计算流程如图4所示。

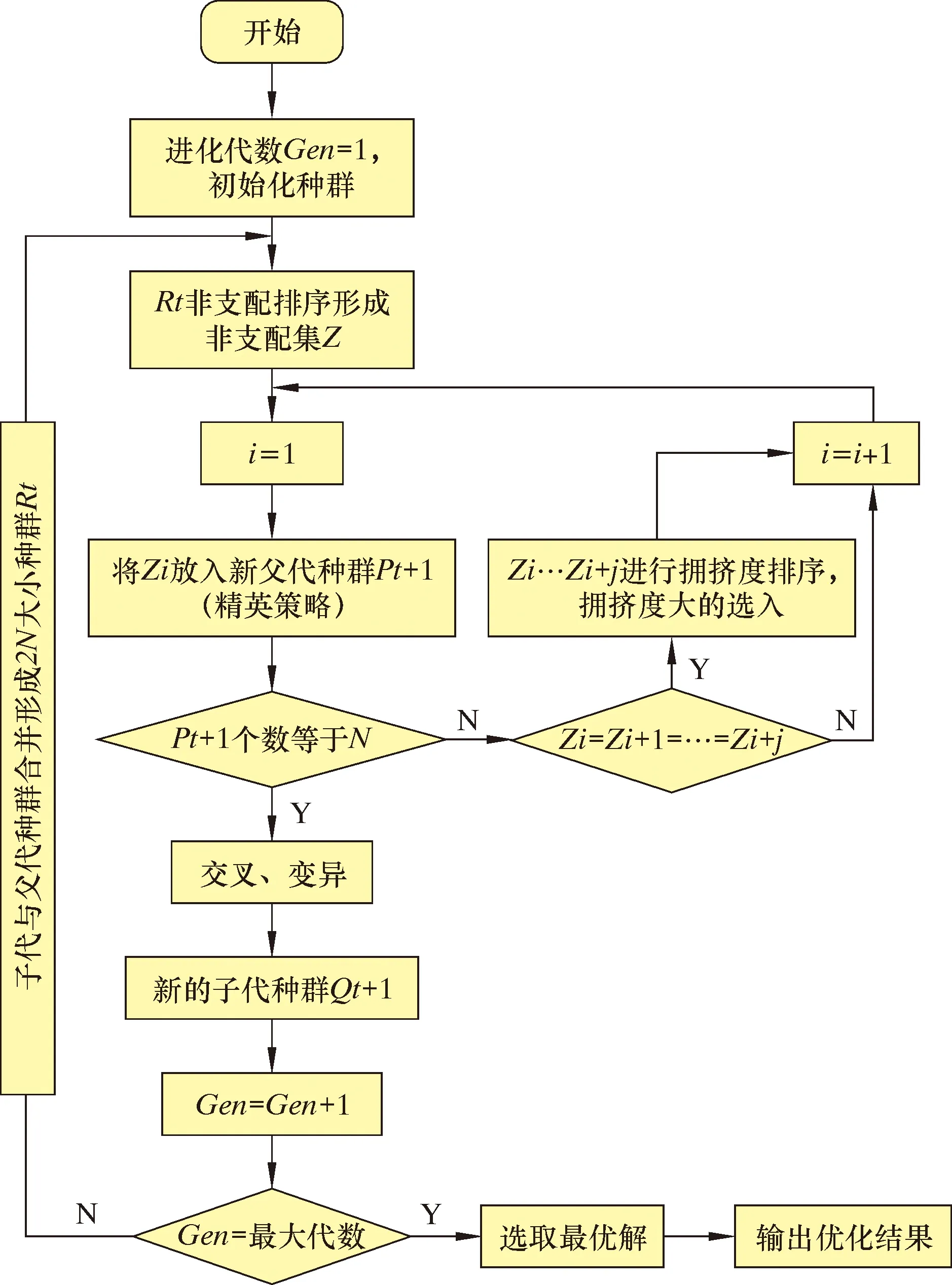
图4 NSGA-Ⅱ计算流程Fig.4 NSGA-Ⅱ calculation process

3.2 基于模糊综合评价法选取最优解

为了在Pareto解集中找出满足条件的最优个体解，还需要对Pareto解集中的个体解做进一步的评价。利用模糊隶属函数，计算个体解对目标函数的隶属度，从而反映个体解对目标函数的优化程度，隶属度越高，代表个体解对目标函数的优化效果越好。隶属度计算公式为：

(12)

将个体解对不同目标函数的隶属度加权之后进行求和，可得到个体解对于多目标函数的总隶属度，总隶属度值最大的个体解即为Pareto解集中的最优解。同时为了保证所有目标函数都得到理想的优化，当个体解代入某一目标函数的值大于设定上限时，采用一票否决制，将该个体解的总隶属度置为0。第k个解的总隶属度计算方法为：

(13)

式中：Nobj为目标函数的总数，λj为j目标函数的加权系数。

4 算例分析

以如图5所示的扩眼器为例，进行布齿优化设计。扩眼器刀翼数为3，切削齿初始后倾角为10°，领眼直径为216 mm，扩眼直径为311.2 mm，设计转速为60 r/min，设计机械钻速为15 m/h，待钻地层可钻性级值为4。

图5 三刀翼扩眼器Fig.5 Three-blade reamer

图6为扩眼器刀翼结构示意图。由图6可知，扩眼器刀翼结构可分为主切削段、保径和倒划眼段，其中主切削段上的切削齿切削量最大，受力也最大，其余刀翼段只起辅助切削作用，对扩眼器侧向力影响很小，因此本文只针对主切削段的切削齿进行布齿优化设计，共计30颗齿。

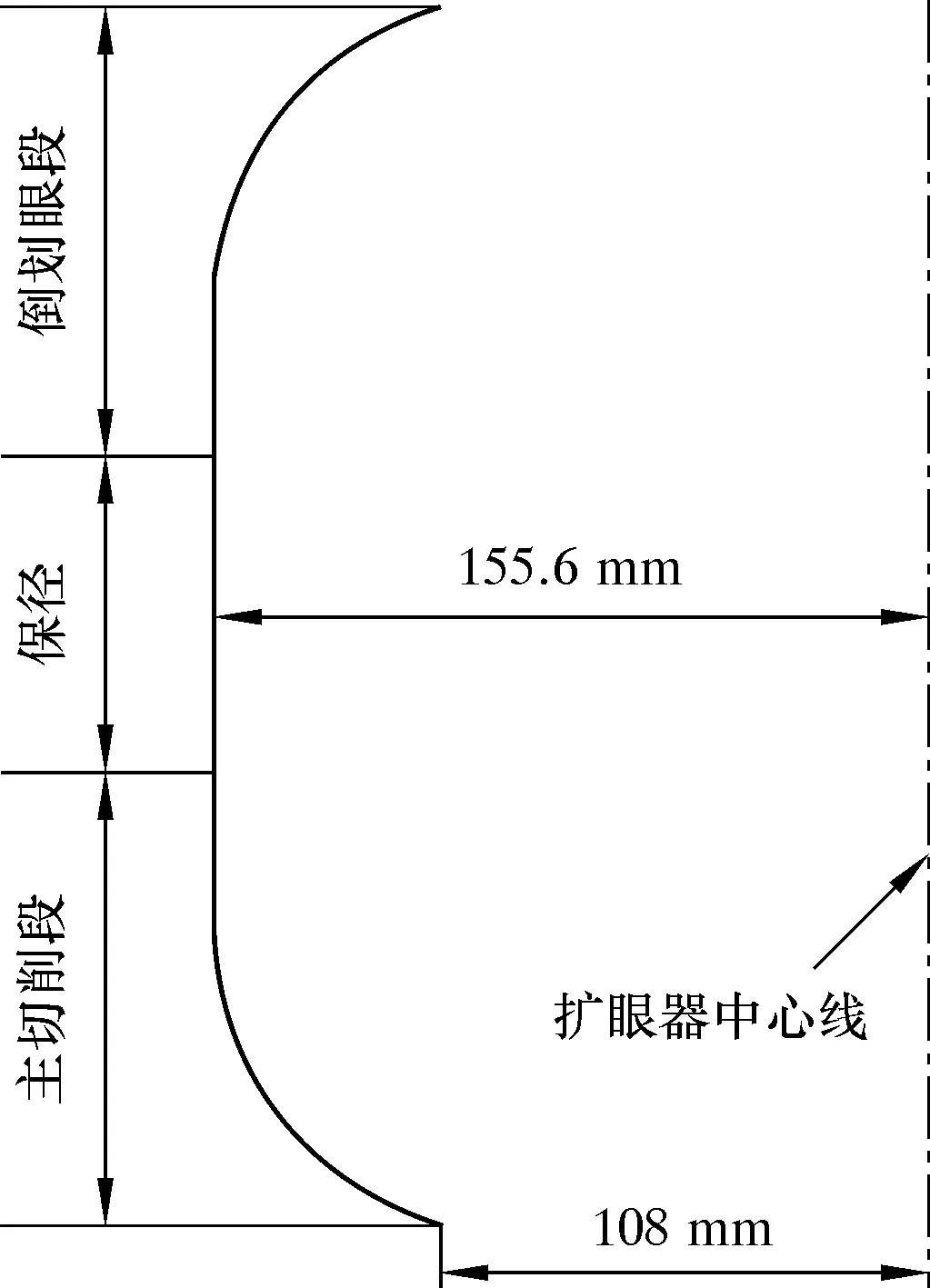
图6 扩眼器刀翼结构示意图Fig.6 Blade structure of the reamer

基于分区法，三刀翼扩眼器的切削过程可分为3个阶段，按照图3所示的计算流程得到3组切削参数，代入式(10)可得布齿优化方程：

(14)

式中：xi为第i颗切削齿后倾角的变化量，αi为优化前第i颗切削齿的后倾角。

本实例采用等权重法计算个体解的总隶属度，并将个体解代入目标函数，函数值上限设为钻压的5%，具体计算公式为：

(15)

式中：P为钻压。

NSGA-Ⅱ算法参数设置如下：种群规模为250，最大进化代数为500，变异概率为0.2，交叉概率为0.8。利用NSGA-Ⅱ算法求解得到满足约束条件的Pareto解集,利用模糊综合评价法计算Pareto解集中所有个体解的总隶属度，最终挑选出最优解。图7为扩眼器布齿优化设计的最优解。图8为优化后的切削齿后倾角。将最优解代入扩眼器受力计算公式，可得到如图9所示的优化前、后的侧向力与钻压比值。从图9可以看出，优化后的各阶段侧向力占比有了大幅度的下降，并且各个阶段的侧向力占比都在5%以内，实现了扩眼器全切削阶段的侧向力平衡。

图7 扩眼器布齿优化的最优解Fig.7 The optimal solution of the reamer cutter layout optimization

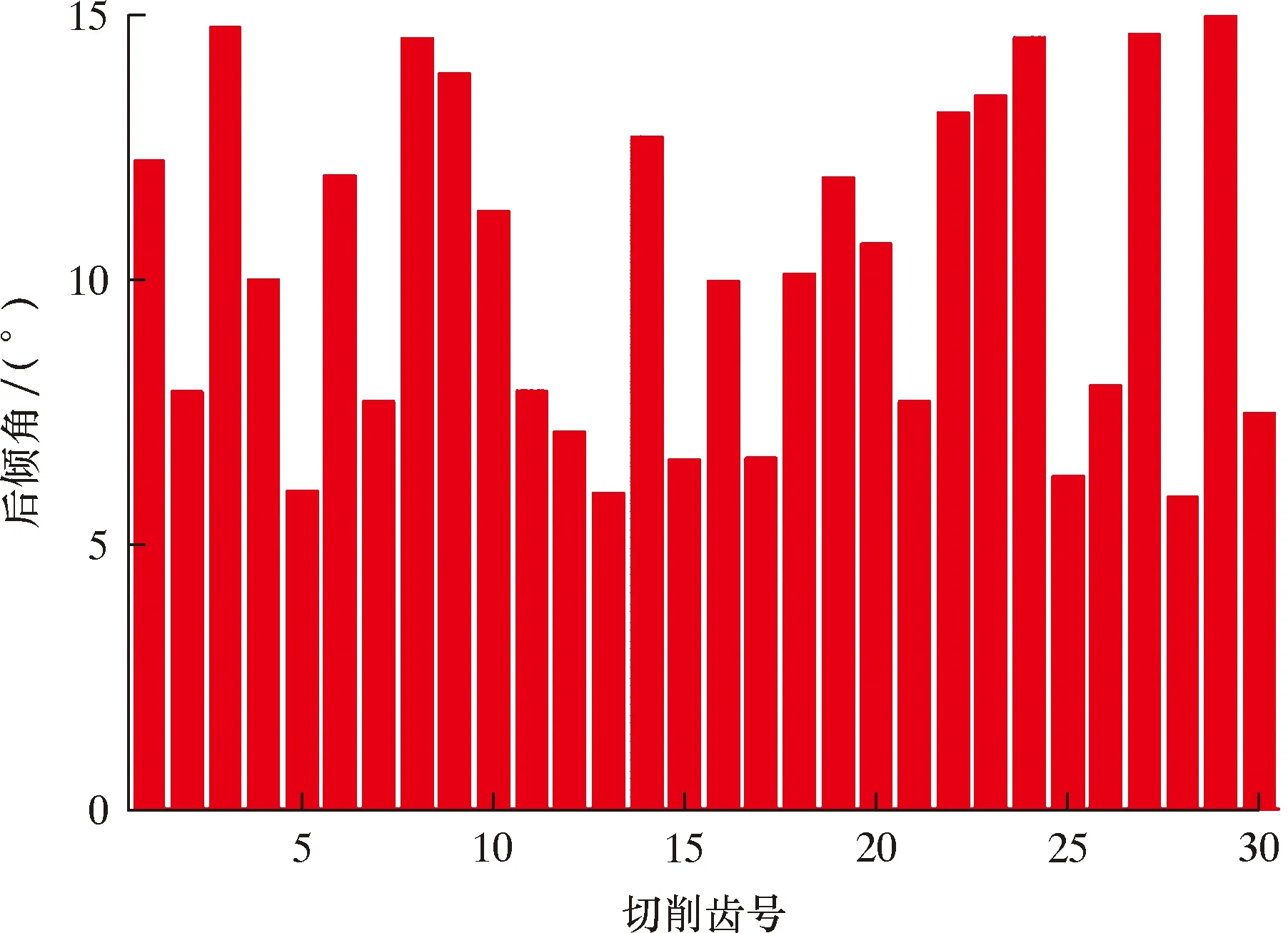
图8 优化后的切削齿后倾角Fig.8 The optimized back rake angle of the cutter

图9 优化前、后的侧向力与钻压比值Fig.9 The ratio of lateral force to WOB before and after optimization

5 结 论

(1)提出了新的切削过程分析方法——分区法。将扩眼器旋转切削破岩一圈的过程划分为不同的切削阶段，不同的切削阶段对应不同的切削受力，依次对各个切削阶段进行分析，可以得到更准确的扩眼器切削受力。

(2)基于分区法进行了各切削阶段的切削参数计算，建立了以各阶段侧向力最小为目标，以各切削齿后倾角为优化变量的多目标布齿优化模型。

(3)利用NSGA-Ⅱ对多目标优化模型进行求解得到最优Pareto解集，基于模糊综合评价法建立了对Pareto解集中个体解的评价方法，从而选取了最优个体解。

(4)以三刀翼扩眼器为例进行了刀翼布齿的优化设计。优化结果表明，基于分区法的布齿优化模型可以有效地减小各个切削阶段的侧向力，并将侧向力与钻压的比值保持在5%以下，从而实现扩眼器的全切削阶段侧向力平衡。