高产曲井油管柱疲劳试验及疲劳寿命分析*
2021-04-23柳军李建郭晓强魏安超黄亮王国荣
柳军 李建 郭晓强 魏安超 黄亮 王国荣
(1.西南石油大学 2.中海石油(中国)有限公司湛江分公司)
0 引 言
随着浅层油气资源的日益减少,我国钻井、完井工艺不断向高压、高温和复杂的深部地层方向发展,并以高产的开采方式才能够满足当前的需求。与常规油气井油管柱相比,高产气井油管柱面临更大的风险[1],主要表现为管内高速气体诱发管柱的非周期性剧烈振动,并产生复杂的交变应力,易导致油管发生疲劳失效[2]。一旦油管柱发生破坏,将被迫井下作业,甚至导致井筒报废,造成严重的经济损失和环境污染。
早期学者针对内流作用下的管柱振动问题开展了初步研究[3],通过试验验证了内流对管柱的动力响应有显著影响[4]。随后,诸多学者针对管柱振动模型开展了详细的研究,建立了流体作用力的计算方法[5]、管柱纵向振动模型[6-7]、横向振动模型[8-9]以及流固耦合振动模型[10-11]。近年来,有学者发现细长管柱的纵横向耦合效应明显,且不可忽略[12]。因此,LIU J.等[13]采用能量法和哈密顿原理建立了考虑井眼轨迹变化、内流冲击、油套管接触碰撞和纵横向耦合作用的高产曲井油管柱非线性振动模型。针对管柱疲劳寿命分析方法的研究,J.A.HOWARD等[14]分析了油管柱振动疲劳失效问题,提出了管柱全寿命预测方法和裂纹扩展分析方法。黄桢[15]发现气井管柱在内流激励下的振动会缩短其疲劳寿命,但未给出管柱疲劳寿命的分析方法。基于此,吴睿等[16-18]借助数值分析技术,建立了气井直管柱疲劳寿命预测模型,但同时考虑油套管接触作用和纵横向耦合效应的高产曲井油管柱流致振动疲劳寿命相关研究还未见报道。
本文首先建立内流冲击、油套管接触碰撞和纵横向耦合作用下的高产曲井油管柱振动疲劳寿命分析方法;接着开展疲劳试验测定油管柱材料13Cr-L80的S-N曲线并进行修正;最后以南海西部某气田为例,分析两口典型的曲井(水平井和定向井)管柱在不同产量和不同油管尺寸下的疲劳寿命。研究结果可为高产曲井油管柱的设计及现场作业提供有效的分析工具和理论依据。
1 油管柱疲劳寿命分析方法
随着现场气井产量的增加,管内高速气体易诱发油管柱发生非线性流致振动,产生复杂的交变应力。为此,笔者在前期的研究中[13]根据现场油管柱的实际情况,采用能量法和哈密顿原理建立了考虑井眼轨迹变化、内流冲击、油套管接触碰撞和纵横向耦合作用的高产曲井油管柱非线性振动模型:
(1)

(2)
式中:x表示管长方向;u表示横向位移,m;w表示纵向位移,m;ρ表示管材密度,kg/m3;ρ0表示内流密度,kg/m3;A表示管柱横截面积,m2;E表示弹性模量,Pa;I表示截面惯性矩,m4;v表示内流速度,m/s;t表示时间,s;f和p分布表示横向外力和纵向外力,且与井斜角有关,N。
通过动力学分析,得到管柱轴向交变应力,再统计出轴向交变应力的应力幅和应力循环次数。本文采用雨流计数法[19-20]对油管柱交变应力进行统计。统计出管柱所有应力循环的应力幅、平均应力及循环次数之后,由于存在平均应力不为0的应力循环,这些应力循环不能直接等效为管柱应力循环,所以需要考虑平均应力的影响。选用古德曼公式[21]进行修正。
古德曼公式:
(3)
式中:σar表示等效应力幅,σa表示应力幅,σm表示平均应力,σs表示材料屈服强度,单位均为MPa。
统计出所有应力循环后,采用Miner疲劳累积损伤理论[22]对油管柱进行疲劳寿命分析。疲劳寿命分析步骤如下:
(1)计算油管柱每个应力循环造成的损伤。统计出油管柱在使用期T′内所有应力循环的应力幅值σ1,σ2,σ3……,和相应的作用次数n1,n2,n3……;根据管材的S-N曲线得到各个应力幅值单独作用时的循环次数N1,N2,N3……,于是可以得到每个应力循环造成的损伤程度n1/N1,n2/N2,n3/N3……。
(2)计算疲劳损伤总量。将所有的应力循环损伤相加可得油管柱在使用期T′内疲劳损伤总量D:
(4)
(3)计算油管柱疲劳寿命L′。
(5)
最终得到高产曲井油管柱疲劳寿命分析流程简图,如图1所示。由图1可知,计算疲劳寿命需要管材的S-N曲线。因此,接下来开展疲劳试验测定管材13Cr-L80的S-N曲线。
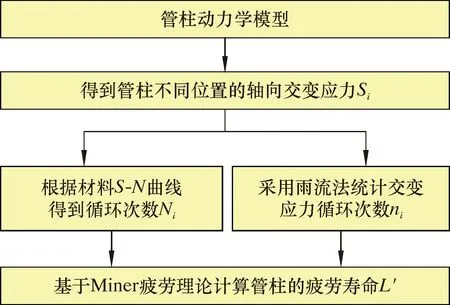
图1 油管柱疲劳寿命分析流程简图Fig.1 Fatigue life analysis process of tubing string
2 S-N曲线的试验测定及修正
2.1 试验设备和试件
此次疲劳试验采用PQ-6型弯曲疲劳试验机。图2为试件受力分析图。试件两端由夹具夹持,试验采用砝码加载。试件的最小直径为d,则可以计算出加载砝码的重力:
(6)
式中:F′表示加载砝码的重力,N;L表示力臂度,即L1和L2,m;σ表示试件承受的应力,MPa;G表示砝码盘和力架等附加重力,N。

图2 试件受力分析图Fig.2 Force analysis of test piece
毛坯按图3进行加工,并通过磨削和抛光等工艺精加工成标准疲劳试验试件。

图3 疲劳试件图片Fig.3 Fatigue test piece
2.2 试验原理和步骤
此次疲劳试验依照GB/T 4337—2015[23]执行,结果如图4所示。测定S-N曲线需分两部分完成:有限疲劳寿命区和无限疲劳寿命区。

图4 测定S-N曲线示意图Fig.4 Determined S-N curve
2.2.1 有限疲劳寿命区
管材(13Cr-L80)的屈服极限σs=600 MPa,初步设定7个应力幅值,即S=585、535、485、435、425、415和405 MPa。每个应力幅值下测定3个试件,记录每个试件发生断裂时的循环次数N,将3个试件的平均循环次数作为该应力幅值对应的循环次数N,共测定21个试件。若在最小应力幅作用下还未有试件的循环次数超过107,则减小应力幅值S,继续试验,直到出现循环次数N大于107。由此,根据试验结果可以推测出疲劳极限的范围,并得到有限疲劳寿命区的S-N曲线。
2.2.2 无限疲劳寿命区
由前一步试验得到的疲劳极限范围来确定试验初始应力幅S,采用9个试件的升降法来测定疲劳极限,得到疲劳极限即测定出无限疲劳寿命区。对第一根试件进行判断,若第一根试样失效,则减小应力值。反之,则增大。从第一次出现相反情况时开始计算,判断出无效的试件,最终由有效试件的数据计算出13Cr-L80的疲劳极限,从而得到无限疲劳寿命区的S-N曲线。为保证准确测定,备用6根试件,共15根试件。
试验步骤如下:
①测量试件最小直径d;②根据确定的应力水平σ,由式(6)计算应加砝码的重力F′;③将试件安装于套筒上,拧紧两根连接螺杆,使之与试件成为一个整体;④连接挠性连轴节;⑤加上砝码;⑥开机前托起砝码,在运转平稳后,迅速无冲击地加上砝码,并将计数器调零;⑦试件断裂或试验次数超过107,记下次数N。
2.3 试验结果
表1为有限疲劳寿命区的试验数据。从表1可以看出,随着应力幅值的减小,循环次数呈数量级增大,在应力幅S为405 MPa时,其平均应力循环次数N为7.9×106,并且该应力幅下有一个试件的循环次数N大于107,从而可以推测出此材料的疲劳极限存在范围为385~415 MPa。

表1 有限疲劳寿命区的试验数据Table 1 Test data of finite fatigue life area
表2为疲劳极限区的试验数据。由表2中的应力等级可以计算出材料的疲劳极限为402.78 MPa。

表2 疲劳极限区试验数据Table 2 Test data of fatigue limit area
2.4 试验结果分析及修正
将表1和表2中的试验结果在双对数坐标系上拟合出管材13Cr-L80的有限疲劳寿命区的S-N曲线,并得到其拟合方程,如图5所示。
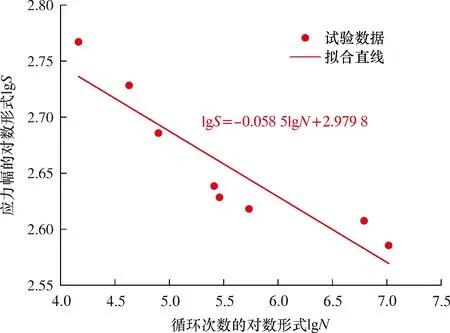
图5 有限寿命区的S-N曲线Fig.5 S-N curve of finite life area
通过试验得到管材13Cr-L80标准试件的S-N曲线之后,为了使曲线更符合现场管柱结构的疲劳失效情况,根据文献[21]从以下4个方面对试验所得的S-N曲线进行修正。
2.4.1 加载类型修正系数CL
在实际工况中,油管柱受到的是纵横向耦合作用,而试验中的试件只受到纯弯曲作用。因此,需要对试验测得的S-N曲线进行修正。修正系数如表3所示。由表3可知修正系数CL=0.7。

表3 修正系数CL[21]Table 3 Correction coefficient CL[21]
2.4.2 试样尺寸修正系数CD
试件尺寸越大,越不易发生疲劳断裂。具体判断依据如下:
当d<8 mm时,CD=1.0;当8 mm 2.4.3 理论应力集中系数Kt和有效应力集中系数Kf 不同的表面粗糙度Ra会在试件表面造成不同程度的应力集中,文献[21]中提出了考虑试件表面粗糙度影响下的应力集中系数公式: (7) 式中:ρ表示微裂纹底部的曲率半径,ρ=39 mm;λ表示微裂纹的间距与深度的比值,取1;q表示切口灵敏度系数,取0.99。 检测得到试件表面粗糙度Ra=6.625 μm,由式(7)可得出有效应力集中系数Kf=1.024 8。 2.4.4 表面质量修正系数CS 管柱疲劳裂纹主要在管柱的自由表面上萌生,因此需要考虑试件的表面质量对裂纹产生的影响。已知试件表面粗糙度Ra=6.625 μm,查文献[21]可知表面质量修正系数CS=0.82。 综合表面粗糙度、缺口效应、加载类型、可靠性系数、表面质量系数和尺寸系数,修正公式为: (8) 式中:Sbe表示标准S-N曲线的应力,MPa;Se表示修正后S-N曲线的应力,MPa。 修正前后的管材S-N曲线如图6所示。由图6可见,修正后的曲线与修正前相比,斜率不变,纵轴截距减小,表明利用修正后曲线得到的疲劳寿命更短。 图6 修正前、后有限寿命区的S-N曲线Fig.6 S-N curve of finite life area 采用Fortran语言,编制高产曲井油管柱疲劳寿命分析方法的计算代码,以南海西部某气田的两口典型曲井(水平井和定向井)为例,分析产量和油管柱尺寸对油管柱疲劳寿命的影响规律。 A1H水平井的井身结构图如图7所示。管柱总长3 500 m,生产封隔器和中部封隔器的位置为3 045和3 500 m,井斜角为0.00°~90.89°。 计算参数:油管密度为7 850 kg/m3;气体密度为275 kg/m3;套管内径为165.8 mm;两种油管柱尺寸分别为外径114.3 mm、壁厚7 mm和外径88.9 mm、壁厚6.5 mm;产量Q分别为4.0×105、6.0×105、9.0×105、1.2×106和1.6×106m3/d;时间取50 s,步长0.002 s,离散为100个单元。 1—油管挂;2—油管;3—套管;4—生产封隔器;5—中部封隔器。 3.1.1 产量对管柱疲劳寿命的影响 图8 不同产量下ø114.3 mm管柱的交变应力曲线Fig.8 Alternating stress of ø114.3 mm string under different production rates 由图8可知,由于自重,上端管柱主要受拉应力作用,下端管柱受压应力作用,上端管柱的交变应力随产量的增加而减小,下端管柱的压应力却随产量增加而增大。其主要原因是随着产量的增加,上端绷紧状态下的管柱横向振动加剧,牵制了纵向振动,导致上端拉应力减小,同时增加了下端管柱的压应力。 图9为A1H水平井ø114.3 mm管柱不同产量下的最大应力和疲劳寿命。由图9a可知:管柱下端受坐封力和流体力作用,在管柱中部偏上位置存在中和点(既不受拉也不受压),并且由于管柱下端气体温度更高、冲击力更大,下端的压应力比上端的拉应力大,导致下部管柱更加容易发生疲劳失效;下部最大压应力值随产量的增加而增大,导致管柱疲劳寿命随产量的增加而缩短,小产量时变化不明显,当产量由1.2×106m3/d增加到1.6×106m3/d时,管柱寿命发生大幅度缩短,产量为1.6×106m3/d时,保持一直不断的生产,管柱的疲劳寿命仅有3.8 a,无法达到现场油气藏配产的使用年限要求(20 a)。 图9 不同产量下ø114.3 mm管柱的最大应力和疲劳寿命Fig.9 Maximum stress and fatigue life of ø114.3 mm string under different production rates 3.1.2 管柱尺寸对管柱疲劳寿命的影响 图10为水平井ø88.9和ø114.3 mm管柱在6.0×105m3/d产量下的交变应力曲线。由图10可知,ø88.9 mm管柱的交变应力显著大于ø114.3 mm管柱的交变应力。其主要原因是管径越大,油套管间隙越小,更加容易发生油套管接触碰撞,增大轴向方向的摩擦力,从而阻碍油管柱轴向运动,使交变应力幅值更小。 图10 水平井不同尺寸管柱的交变应力曲线Fig.10 Alternating stress of different sizes of strings 图11为不同尺寸管柱在产量为6.0×105m3/d时的最大应力和疲劳寿命。由图11可知,水平井ø88.9 mm管柱和ø114.3 mm管柱均在管柱下端出现较大的应力幅值,且ø88.9 mm管柱的最大压应力大于ø114.3 mm管柱的最大压应力,导致小尺寸管柱的使用寿命显著短于大尺寸管柱。这表明小尺寸管柱更易发生疲劳失效,当产量为6.0×105m3/d时,ø88.9 mm管柱的使用寿命约为22.9 a,能够满足现场的使用要求。 图11 水平井不同尺寸管柱的最大应力和疲劳寿命Fig.11 Maximum stress and fatigue life of different sizes of strings 前面分析了水平井管柱疲劳寿命的影响规律,下一步采用南海西部典型定向井(A3气井)现场参数,分析定向井管柱疲劳寿命的变化规律。该定向井井身结构如图12所示。管柱总长为4 000 m,生产封隔器位置为3 766 m,中部封隔器位置为4 000 m,井斜角为0.00°~43.44°,其余参数与水平井计算参数相同。 1—油管挂;2—油管;3—套管;4—生产封隔器;5—中部封隔器。 3.2.1 产量对管柱疲劳寿命的影响 图13为定向井ø114.3 mm管柱在不同产量下的交变应力曲线。由图13可知,随着产量的增加,上端管柱的拉应力存在微小变化,影响并不明显,下端管柱的压应力却发生显著的变化,其变化机理与水平井相同。 图13 管柱在不同产量下的交变应力曲线Fig.13 Alternating stress of string under different production rates 图14为定向井ø114.3 mm管柱在不同产量下的最大应力和疲劳寿命。 图14 管柱在不同产量下的最大应力和疲劳寿命Fig.14 Maximum stress and fatigue life of string under different production rates 由图14可知:水平井管柱依然上端受拉、下端受压,下部管柱出现的压应力幅值更大,更加容易发生疲劳失效;随产量的增加,下部管柱的压应力发生显著增大,导致寿命出现缩短的趋势,且当产量为1.6×106m3/d时,管柱疲劳寿命最短,在生产封隔器处的疲劳寿命约为1.8 a。 3.2.2 管柱尺寸对管柱疲劳寿命的影响 图15为定向井ø88.9和ø114.3 mm管柱在产量为6.0×105m3/d时的交变应力曲线。由图15可知,ø88.9 mm管柱的交变应力同样显著大于ø114.3 mm管柱的交变应力,其变化机理与水平井相同。 图15 定向井不同尺寸管柱的交变应力曲线Fig.15 Alternating stress of different sizes of strings 图16为定向井ø88.9 mm管柱和ø114.3 mm管柱的最大应力和疲劳寿命。由图16可知,ø88.9 mm管柱的疲劳寿命短于ø114.3 mm管柱的疲劳寿命,且当产量为6.0×105m3/d时,其疲劳寿命为8.5 a,无法满足现场油藏的使用要求。 图16 定向井不同尺寸管柱的最大应力和疲劳寿命Fig.16 Maximum stress and fatigue life of different sizes of strings 在分析南海西部2口典型曲井油管柱疲劳寿命变化规律的基础上,通过大量计算,得到水平井和定向井管柱疲劳寿命随产量的变化规律(见图17),进一步提出了现场配产数据。由图17可知,产量越大,油管柱疲劳寿命越短,水平井管柱(ø114.3 mm)达到油气藏年限(20 a)的临界产量为1.1×106m3/d,而定向井管柱的临界产量为4.5×105m3/d。因此,现场作业时,当配产数据低于临界产量时,可以持续生产,当配产数据高于临界产量时,不能长期高产量配产,需后期调整产量,以保证油管的使用寿命。 图17 管柱疲劳寿命随产量的变化规律Fig.17 String fatigue life vs production rate 根据前面水平井和定向井油管柱疲劳寿命的研究成果,提出了现场A1H水平井和A3定向井的配产数据,如图18所示。A1H水平井在生产1 a后,产量从1.6×106m3/d降到7.0×105m3/d,又生产1 a后,产量会降到5.0×105m3/d,最终产量降到6.0×104m3/d;A3定向井在生产1 a后,产量从7.0×105m3/d降到4.0×105m3/d,再生产1 a后稳定在2.0×105m3/d,并且两口井已在2018年投产,本文提出的疲劳寿命分析方法已得到现场应用。 图18 水平井和定向井的现场配产数据Fig.18 Field proration of horizontal wells and directional wells (1)针对高产曲井油管柱流致振动疲劳失效问题,笔者在前期建立的管柱非线性流致振动模型的基础上,结合其交变应力响应和材料的S-N曲线,引入Miner线性疲劳累积损伤理论,形成了高产曲井油管柱疲劳寿命分析方法。 (2)以现场管材13CrL80开展疲劳试验,测定了管材的S-N曲线,并结合现场工况考虑试件表面质量、加载类型、应力集中和加工尺寸的影响修正了管材的S-N曲线。 (3)以南海西部某气田的2口典型曲井(水平井和定向井)为例,分析了油管柱在不同产量(4.0×105~1.6×106m3/d)、不同油管柱尺寸(ø88.9 mm和ø114.3 mm)下的疲劳寿命。研究结果表明:产量越大,管柱疲劳寿命越短;水平井管柱(ø114.3 mm)达到油气藏年限(20 a)的临界产量为1.1×106m3/d,定向井管柱的临界产量为4.5×105m3/d,在产量大于临界产量时,应在管柱危险位置处设置扶正器以延长管柱疲劳寿命;ø88.9 mm管柱相对于ø114.3 mm管柱更易发生疲劳失效。
3 实例分析
3.1 A1H水平井油管柱疲劳寿命分析




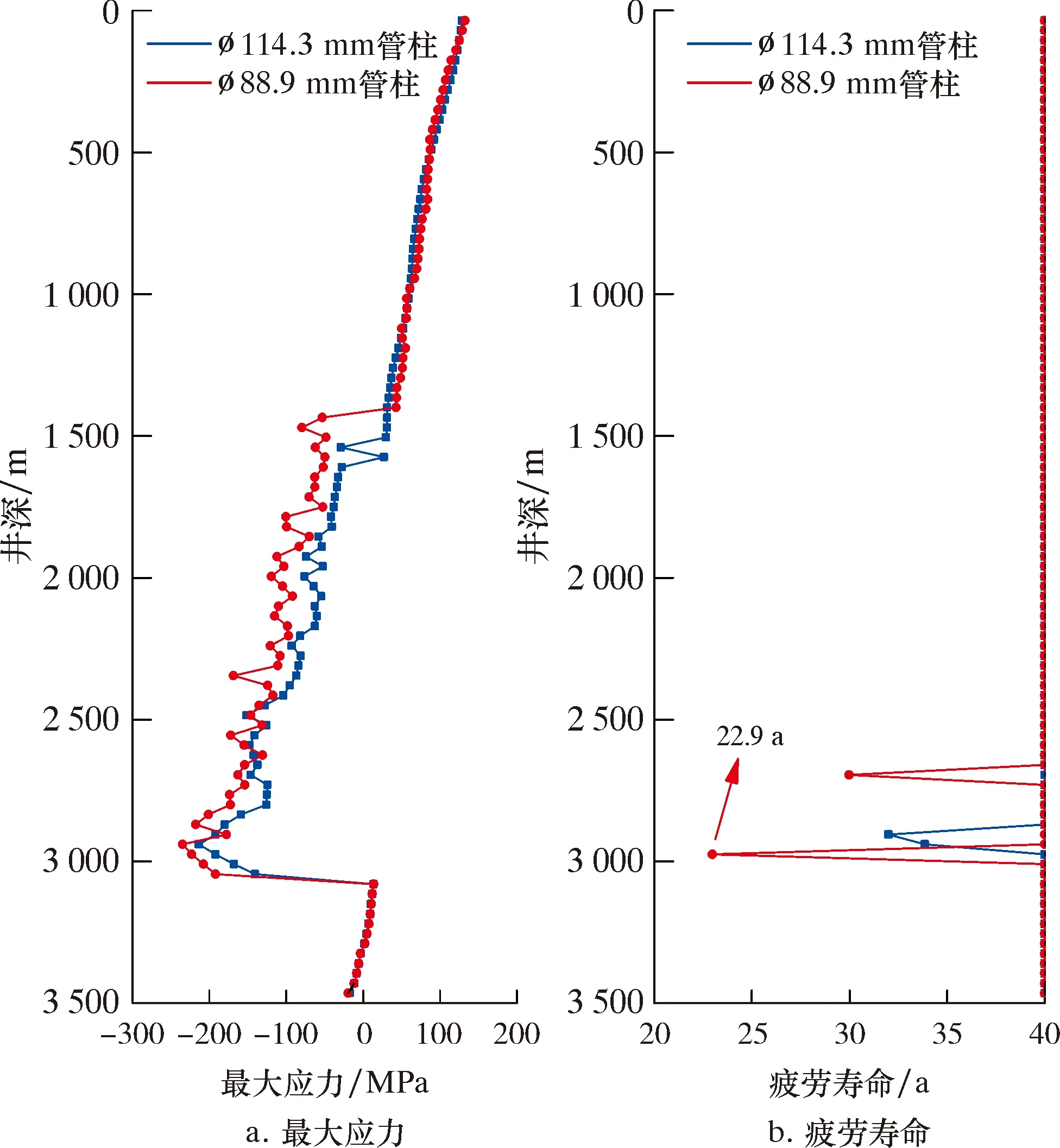
3.2 A3定向井油管柱的疲劳寿命分析

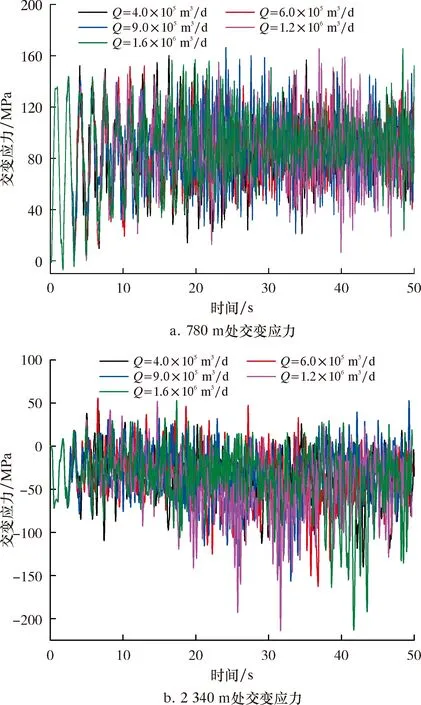

3.3 现场指导

4 结 论
