混合励磁磁通切换直线磁悬浮电动机电磁力的有限元计算
2021-04-23艾春洋蓝益鹏
艾春洋, 蓝益鹏
(沈阳工业大学 电气工程学院,辽宁 沈阳 110870)
0 引 言
轨道交通的牵引系统所使用的电机主要为旋转电机和直线电机[1]。与旋转电机相比,直线电机的驱动方式具有显著优点[2]。无论在中国国内还是国外,直线感应电机驱动在高速铁路运营系统中均得到了广泛的应用,如日本横滨市营地铁4号线、中国广州地铁6号线等。直线感应电机在轨道交通方面应用存在低效率、无功功率占比高等缺点[3]。在长定子轨道交通领域,将永磁体或绕组沿轨道铺设,大幅度增加预算成本,日常的维护也比较困难,这些技术难题亟待解决[4]。
直线电机法向力较大,一般情况下,该法向力可能是电磁推力的数倍。通常主要研究直线电机的水平推力,一般不考虑法向力[5-7],但是磁悬浮列车运行速度非常快,在竖直方向的法向力必须得到很好的控制,使列车能稳定运行。车身本身具有重力,重力的方向和磁悬浮力的方向相反,可以通过调节磁悬浮力的大小与自身车重达到平衡,此时的动子和定子间没有摩擦,达到了稳定运行的目的[8]。在水平方向上,采用直线电机直接驱动方式,可以实现无磨损快速运动。
本文设计的混合励磁磁通切换直线磁悬浮电动机(HEFSLMSM)主要应用于磁悬浮列车牵引系统,该电动机的抱轨结构使动子结构更加复杂,永磁体、励磁绕组以及电枢绕组均位于短动子上,次级长定子仅由导磁铁心构成,用1台电动机能够实现直接驱动和稳定悬浮,同时还具有可调节的气隙磁场。该设计结构具有低成本、坚固耐用等优点,特别适合于长距离的轨道交通[9-10]。
1 HEFSLMSM结构与运行原理
1.1 HEFSLMSM结构
图1为HEFSLMSM结构示意图。永磁体、励磁绕组以及电枢绕组位于初级短动子上。电枢绕组缠绕在2个相邻的U型铁心槽中;直流励磁绕组缠绕在U型铁心上;次级只有铁心材料。永磁体的充磁方向为横向交替充磁,即与运动方向相同或者相反。
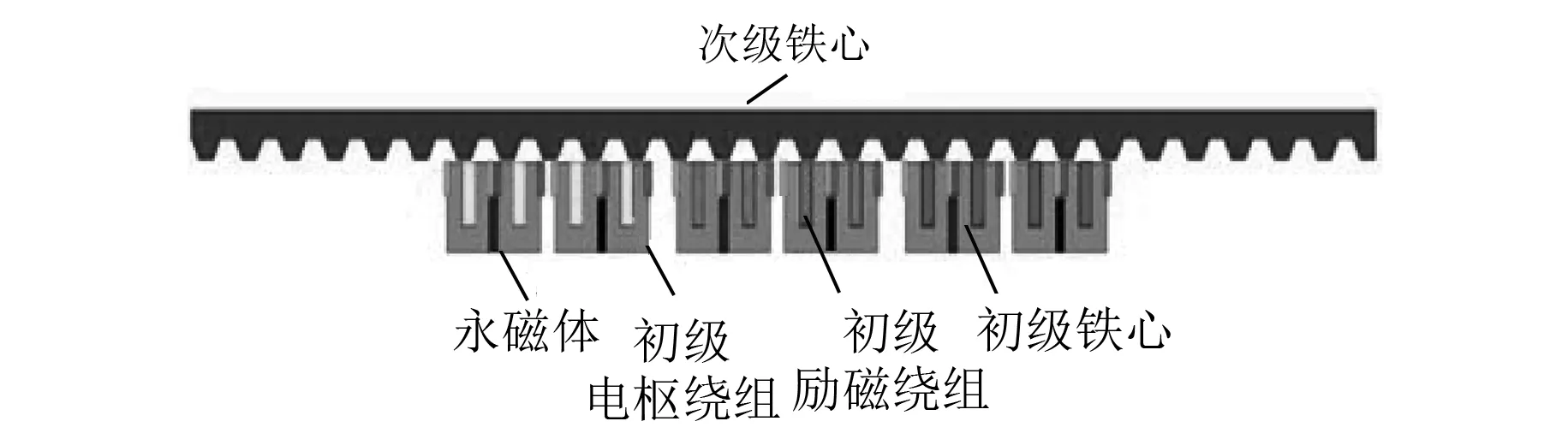
图1 HEFSLMSM结构示意图
1.2 HEFSLMSM的运行原理
1.2.1 磁通切换原理
A相电枢绕组中的磁链能够出现双极性,磁通能够正向穿过A相绕组又能过渡到反向穿过。动子处在4个不同位置时对应的磁通情况如图2所示,由正向最大位置过渡到第一平衡位置(磁通为0),负向磁通最大位置过渡到第二平衡位置(磁通为0)。B、C相磁通变化同理,在此不作赘述。
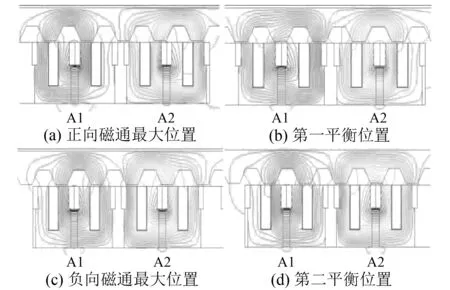
图2 磁场分布
1.2.2 电磁推力产生原理
图3(a)中的磁力线是由永磁体产生的,A1与A2模块处于正磁链的最大位置,也就是图3(b)中M1处,励磁电流产生的磁链和永磁体产生的磁链合成后为总磁链,按照磁通走磁阻最小路径原理,动子向右移动。随着动子的运动,动子齿和定子齿重合部分变大,当两者完全重合时,到达第一平衡位置(磁通为0)。这时A相关断,B相导通,图3(b)所示B相磁链到达最大位置M2处,向右的电磁推力产生原理和A相相同,动子继续向右运动,当B相磁链到达平衡位置时,B相关断,C相开始导通。通过控制电流的导通和关断从而保证动子朝一个方向运动。

图3 电磁推力原理示意图
1.2.3 悬浮力产生原理
当电动机运行过程中,励磁绕组和永磁体均会在气隙中产生磁场,此时气隙中的合成磁场和次级铁心相互作用使铁心被吸起,即悬浮力。当悬浮力与磁悬浮列车的重力大小相等时,即可实现稳定悬浮。
2 建立HEFSLMSM的数学模型
模型的假设条件如下:
(1) 假设电机铁心材料不饱和,不考虑涡流和磁滞带来的影响;
(2) 永磁体与励磁绕组所产生的气隙磁场正弦分布,忽略高次谐波影响;
(3) 通入的电枢电流为三相对称。
在d-q坐标系下的磁链方程:

(1)
式中:Ld、Lq、Lf分别为电枢绕组d轴自感、电枢绕组q轴自感及励磁绕组自感;Mf为单相电枢绕组与励磁绕组之间互感的幅值;ψf永磁体产生磁链。
在d-q坐标系下的电压方程:
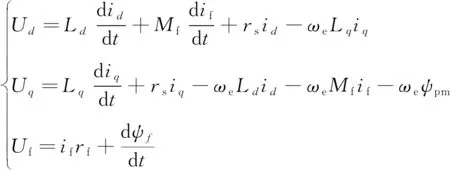
(2)
式中:Ud、Uq分别为电枢d轴电压及电枢q轴电压;Ld、Lq分别为d、q轴电感;id、iq分别为d、q轴电流;if为直流励磁电流;rs为电枢绕组的电阻;Uf为励磁电压;ψf、ψpm分别为励磁磁链和永磁磁链的幅值;rf为励磁绕组的电阻。
电磁推力:电机在运行过程中的功率主要由各项绕组的输入功率组成,当忽略铁耗影响时,该电机的输入功率可表示为

(3)
将式(1)和式(2)代入式(3),可得电动机的电磁推力方程和悬浮力方程:
Fpm+Fr+Ff
(4)
悬浮力方程为

(5)
式中:Fpm为永磁体产生的推力;Fr为磁阻推力;Ff为电励磁推力分量;τs为定子极距;g为气隙长度。
3 电机静态特性的有限元分析
图1中的HEFSLMSM基本参数如表1所示[11]。根据图1和表1在ANSYS软件中设计Maxwell 2D仿真模型。
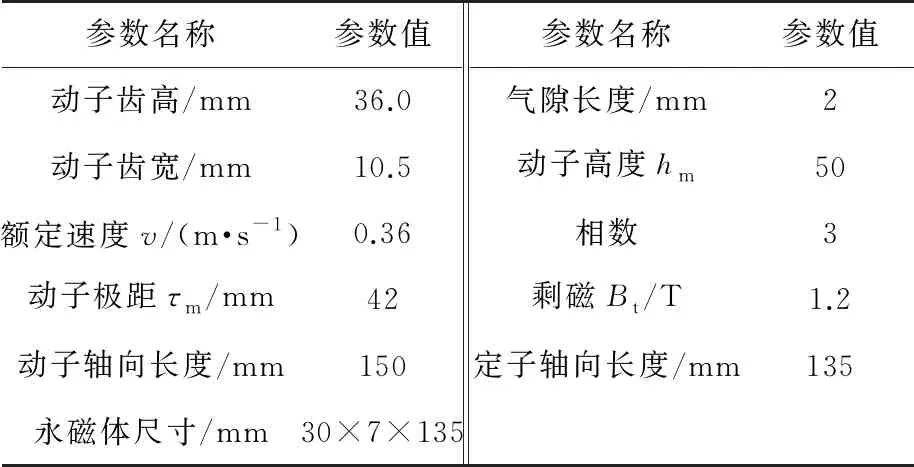
表1 HELMSM基本参数
3.1 磁场分布
图4为HEFSLMSM在空载情况下的磁场分布。利用ANSYS软件分析时,会有一定漏磁的情况,为了不让永磁体与外界空气有接触,可以在电动机模型外增加一个空气区域。由图4可以看出,定子的齿在运动时与动子齿重合的面积越大,说明通过的磁力线越多,磁通越大,漏磁通越小,则电动机效率越高。
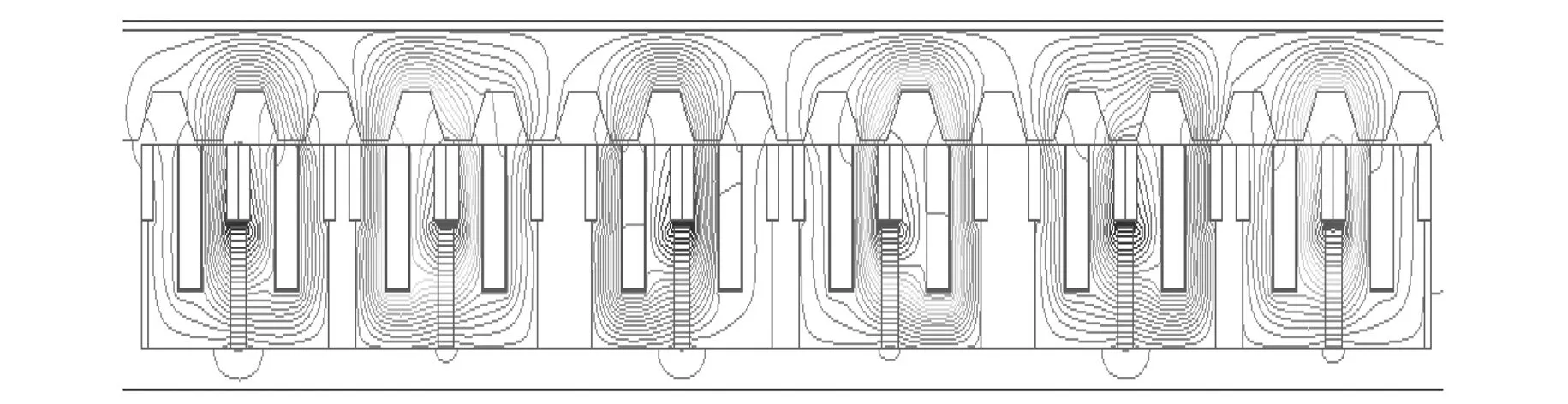
图4 HEFSLMSM空载磁力线分布图
图5(a)为电动机处在空载状态时的磁密云图,可以得到各部分的磁密值;图5(b)为局部磁密云图[12]。

图5 气隙磁密云图
从图6可以看出,HEFSLMSM的气隙磁密约为1.3 T,气隙磁场不是理想的正弦波,原因是初级动子和次级定子均是凸极结构,会产生齿槽效应影响谐波分量,使理想情况下的正弦波发生畸变[13-14]。

图6 气隙磁密
3.2 空载反电动势
图7为HEFSLMSM的三相反电动势波形,接近正弦波。气隙磁密谐波分析如图8所示。由图8可知,由于每相的2个模块通入相同幅值电流,会产生相同幅值的反电动势,相位角的不同影响高次谐波的分量,当相邻2个模块线圈中的反电动势串联叠加后,反电动势波形中的高次谐波分量被抵消掉,只剩下基波分量以及一些幅值非常小的高次谐波分量,从而使得波形更接近正弦波[15-16]。

图7 三相反电动势
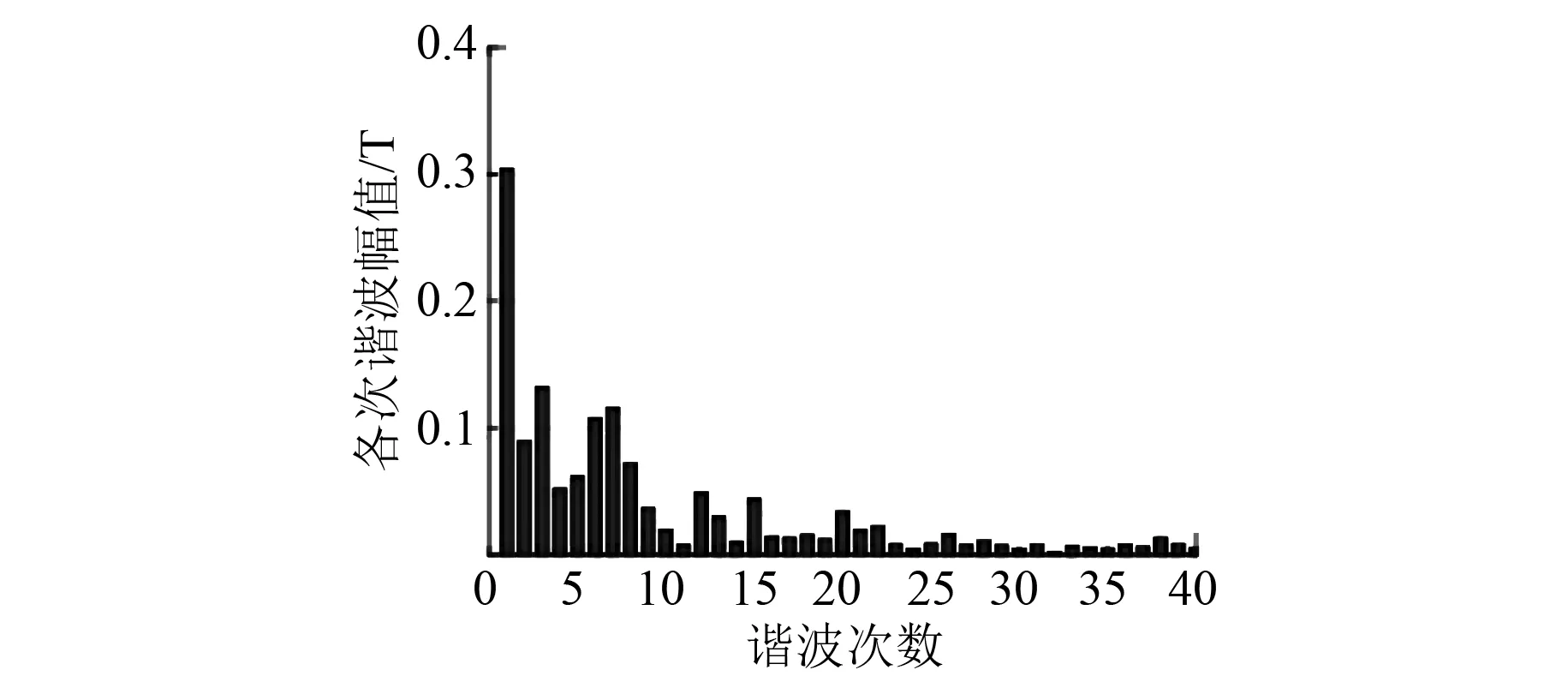
图8 气隙磁密谐波分析
3.3 空载磁链
图9为在HEFSLMSM空载状态下的三相磁链图。由图9可知,磁链正弦,每相磁链的幅值相同,相位相差120°。
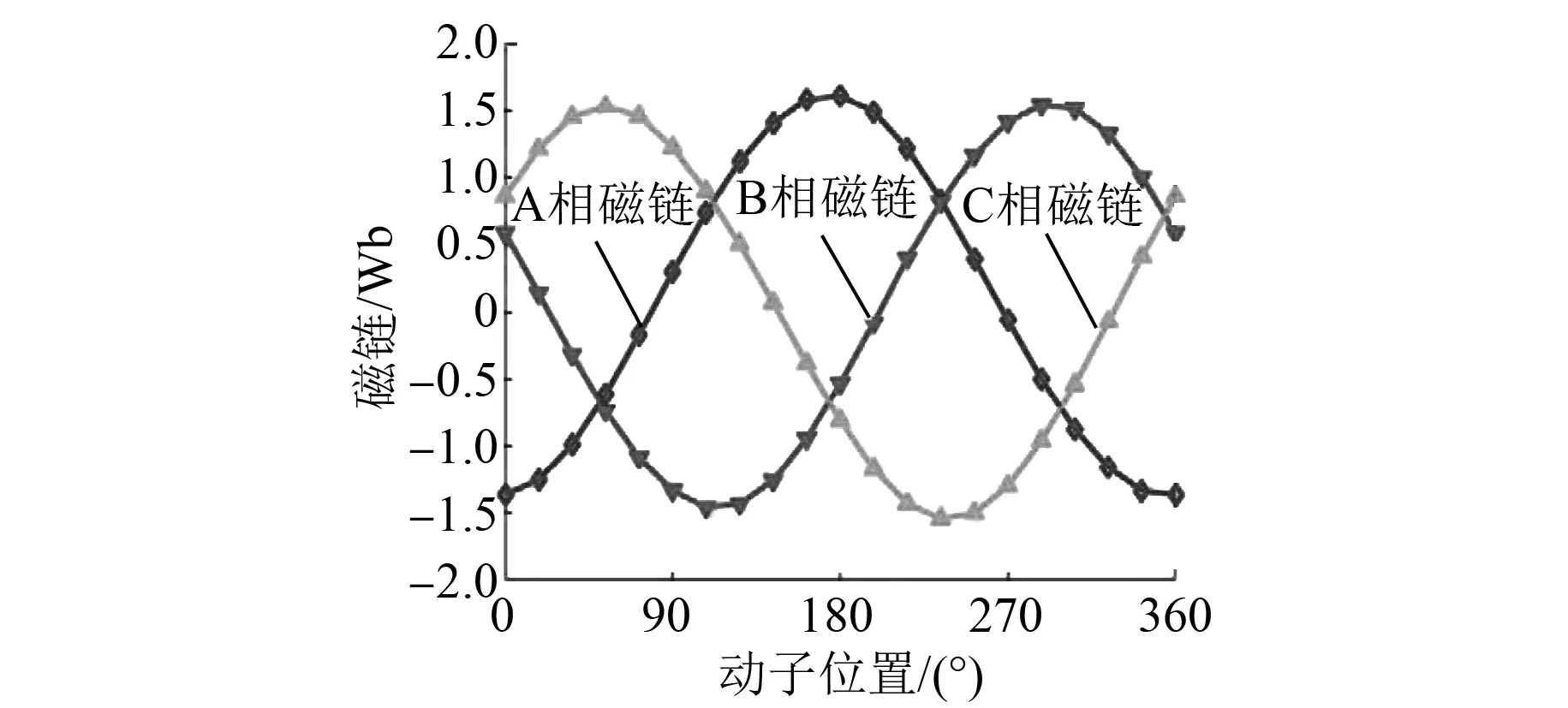
图9 三相空载磁链
3.4 调磁能力
图10和图11所示为电机的调磁性能。图10为在不同直流励磁电流下的A相磁链;图11为在不同直流励磁电流下的A相反电动势。从图10、图11可以看出,励磁电流变化影响磁链和电动势峰值和相位。因此,励磁电流的大小影响磁链和反电动势波形正弦度。
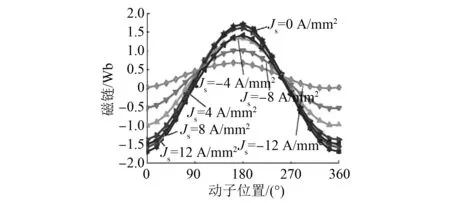
图10 A相磁链

图11 A 相反电动势
4 电磁力的有限元计算
利用ANSYS软件计算出HEFSLMSM模型在不同的励磁电流和电枢电流下的电磁推力和悬浮力[17-20]。
图12为励磁电流为0 A时,电枢电流变化对电磁推力和悬浮力均值变化的曲线。可以看出,电磁推力随电枢电流呈线性增加;悬浮力随电枢电流的变化量较小,当气隙磁场稳定时,电枢电流主要影响HEFSLMSM的电磁推力。

图12 励磁电流为0 A时,电磁力均值随电枢电流的变化曲线
当电枢电流为0 A,电磁推力近乎为零,悬浮力均值随励磁电流变化的曲线如图13所示。HEFSLMSM的悬浮力随励磁电流近似呈线性递增趋势。

图13 电枢电流为0 A,悬浮力均值随励磁电流变化的曲线
电枢电流为5 A时,励磁电流变化对电磁力均值和悬浮力均值变化的曲线如图14所示。可以看出,电磁推力随励磁电流呈线性递增;悬浮力随励磁电流呈线性递增,并且变化量要远大于电磁推力的变化量。当电枢电流一定时,励磁电流主要影响HEFSLMSM的悬浮力。

图14 电枢电流为5 A,励磁电流变化对电磁力均值和悬浮力均值变化的曲线
5 结 语
(1) 研究了HEFSLMSM的基本结构,并对其运行原理进行论述,推导出HEFSLMSM在d-q坐标系中的电压方程、磁链方程、电磁推力和悬浮力的解析表达式。
(2) 该电机采用混合励磁的方式,在有效减小永磁体用量,降低电机成本的同时,引入了电励磁,使得电机具有可调的气隙磁场,通过控制直流励磁电流控制电机的悬浮力,使其稳定悬浮。
(3) 对电磁力和悬浮力进行有限元计算并进行对比,得出电枢电流主要影响电动机的电磁推力,励磁电流主要影响悬浮力。本文所提的新型电动机,因为不需要在导轨上铺设绕组,大幅度减少了成本,所以非常适用于长定子磁悬浮列车场合。
