基于全阶状态滑模观测器的永磁同步电机模型预测电流控制策略

刘向辰, 熊志誉, 薛二桥

(1. 兰州石化职业技术学院 汽车工程学院，甘肃 兰州 730060；2. 湖南兵器轻武器研究所有限责任公司，湖南 益阳 413000)

0 引 言

永磁同步电机(PMSM)具有体积小、调速性能优异、功率密度大等诸多优点，在中国工业生产领域应用较为广泛。针对PMSM控制方法的研究，也是国内外相关领域专家研究的重点。为了解决PMSM PI控制参数整定困难的问题，文献[1]提出一种有限控制集模型预测电流控制(MPCC)[2-3]策略，该策略无需考虑空间电压调制，通过构造电流偏差最优函数，从而对负载突变时的电机转矩进行准确控制。为了实现交流电机转速和转子磁链的精准信息，文献[4]提出一种基于二阶滑模观测器[5-6]的电机转子磁链观测方法，该方法将包含磁链的电流模型改造成参考自适应系统，用于对电机转速进行估测，最终完成电机矢量控制。为了解决超高速飞行器在飞行过程中不稳定的问题，文献[7]将自适应模糊二阶滑模控制器[8-9]用于对超高速飞行器进行姿态调整和控制，解决了飞行器动力学和运动学模型不确定的问题。针对PMSM直接转矩控制开关表失效的问题，文献[10]将电压矢量模糊调节的思想应用到PMSM直接转矩控制[11-12]中，能够有效抑制电机的转矩脉动。

综上，本文提出一种基于全阶状态滑模观测器的PMSM MPCC方案。该方案首先采用一种改进型MPCC方案，与传统MPCC相比，通过采用缩减电压矢量选择的方法，降低了计算量，提高了控制效率。同时，应用一个结合模糊控制思想的全阶状态滑模观测器对PMSM的转子位置和转速进行精准估算，消除了观测过程中存在的转子位置和转速抖振问题，提高了PMSM的控制性能。

1 PMSM MPCC

两相同步旋转坐标系下的PMSM数学模型可以写成：

(1)

式中：id、iq为定子电流的d、q轴分量；R为定子电阻；L为定子电感；ωe为电角速度；ud、uq为定子电压的d、q轴分量；ψ为永磁体磁链。

对式(1)进行离散化处理，可得:

(2)

式中：Ts为系统采样时间。

电机定子电压共有7种组合方式，其合成电压矢量如图1所示。

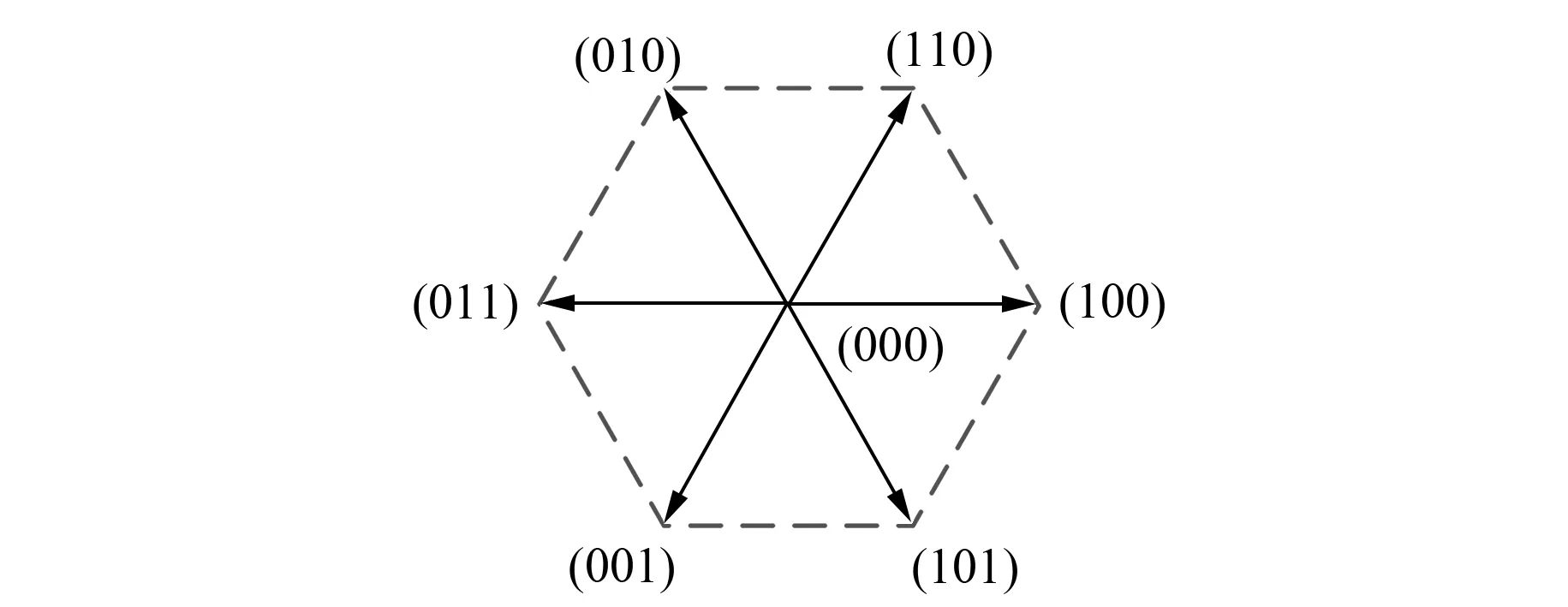
图1 电机定子电压7种组合方式原理图

图1中，(000)表示PMSM三相定子电压uA=uB=uC=0 V；(110)表示uA=uB=UDC，uC=0 V；(111)表示uA=uB=uC=UDC，依次类推。其中，UDC为电机直流母线电压。

MPCC的目标函数可以写成：

(3)

将图1中电机定子的7种电压矢量组合形式所对应的电流值代入式(3)，选取使目标函数最小(即实际电流与参考给定电流差最小)的电压矢量组合，用该组定子电压对逆变器开关进行控制，可以达到良好的控制效果。

由于传统MPCC采用的是最优电压矢量枚举法，需要对所有的电压矢量组合进行动态预测，计算量大。针对这一问题，本文采用一种改进型最优电压矢量选择方法，缩减了电压矢量选择的范围，降低了计算量，提高了控制效率。

对零电压矢量组合控制下的参考给定电流与预测电流作差，可以写成：

(4)

根据PMSM实际控制的要求，设定一组电流误差最小值γd、λq，若|ed0|≤γd且|eq0|≤γq，则最优电压矢量选择零电压矢量，若不满足上述条件，最优电压矢量就从其他电压矢量中选择。

对非零电压矢量组合控制下的参考给定电流与预测电流作差，可以写成：

(5)

对式(4)、式(5)进行化简，可得：

(6)

由于MPCC的目标是保证ed、eq尽可能小，令ed=eq=0，可得：

(7)

对式(7)进行化简，可得：

(8)

因此，可以得到非零电压矢量与d轴的夹角α为

(9)

非零电压矢量与空间参考A轴的夹角β为

β=[α+θe%(2π)]%(2π)

(10)

式中：θe为电机转子的位置角；%为取余运算。

在选择电压矢量时，一般选取最接近最优非零电压矢量作为控制电压组合，因此需要重新划分定子电压扇区划分，保证每个区域均有一个非零电压矢量。重新划分后的电压合成矢量原理如图2所示。

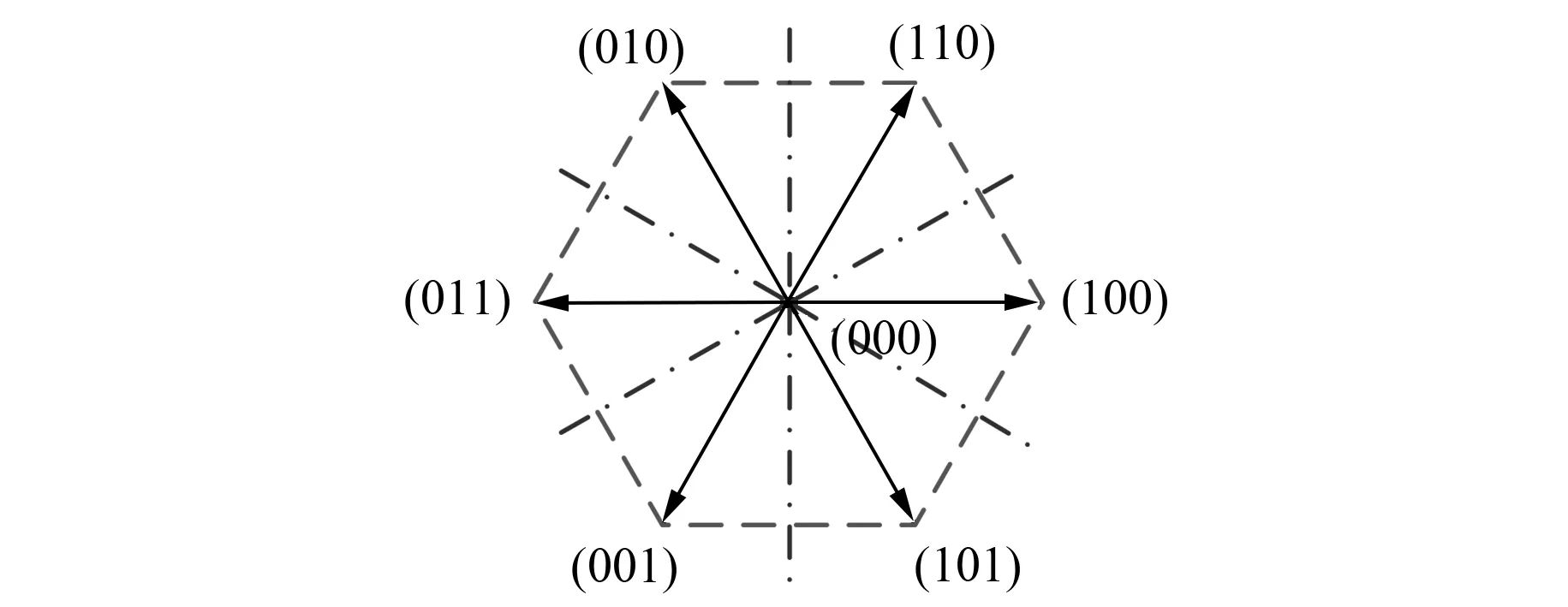
图2 重新划分后的电压合成矢量原理图

2 基于全阶状态滑模观测器的PMSM MPCC

在MPCC过程中，还需要准确估算出PMSM的电机转子位置和电机转速。由式(1)可得在αβ两相静止坐标系下的电机数学模型：

(11)

式中：Eα、Eβ为定子电压的αβ轴分量，且Eα=-ψωesinθe、Eβ=ψωecosθe。

从式(11)可以看出，Eα、Eβ中含有电机转速和转子位置信息，为了从反电动势的众多高频噪声信号中准确提取出转速和转子位置信号，一般采用滑模观测器，但传统滑模观测器观测精度低且存在抖振，为了解决这一问题，在传统滑模观测器中结合模糊控制的思想。

由于PMSM在一个工作周期内转速的变化率很小[13]，则dωe/dt=0，反电动势方程可以写成:

(12)

由式(11)和式(12)，可以写出PMSM全阶状态方程：

(13)

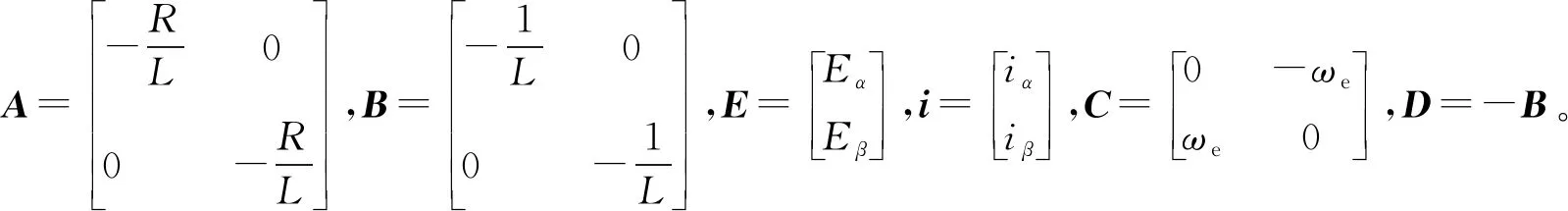
由式(13)可以写出PMSM全阶状态滑模观测器方程:

(14)

sgn可以表示成：

(15)

式中：α为滑模观测器切换函数sgn的边界层系数，α的选取应该考虑到尽可能降低系统抖振和系统响应时间。

通过构造Lyapunov函数，为了保证系统稳定，全阶状态滑模观测器的反馈增益矩阵G需要满足条件:G>max(|Eα|，|Eβ|)。

表1 模糊控制规则

令输入、输出统一化论域为{-3、-2、-1、0、1、2、3}。

模糊自适应滑模控制的主要作用是可以使系统误差快速趋近于零，且到达滑模平面附近时，尽可能稳定，最大限度减小抖振。

模糊自适应滑模控制的隶属度函数曲线如图3所示。

图3 隶属度函数曲线

基于模糊自适应思想的全阶状态滑模观测器如图4所示。

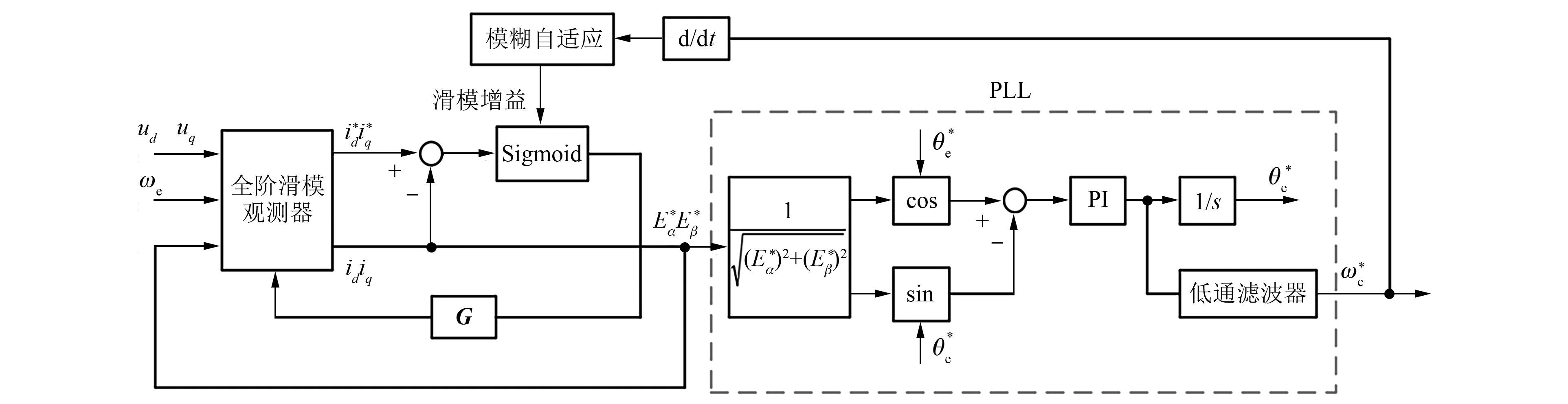
图4 全阶状态滑模观测器原理图

3 仿真分析

为了验证所提理论的正确性，在MATLAB/Simulink中搭建了电机控制仿真模型。PMSM仿真参数如下：额定功率1.5 kW、定子d轴电感Ld=1.85 mH、定子q轴电感Lq=5 mH、永磁体磁链为0.1 Wb、定子电阻R=0.5 Ω、转动惯量0.001 kg·m2、极对数为2。

基于全阶状态滑模观测器的PMSM MPCC原理如图5所示。

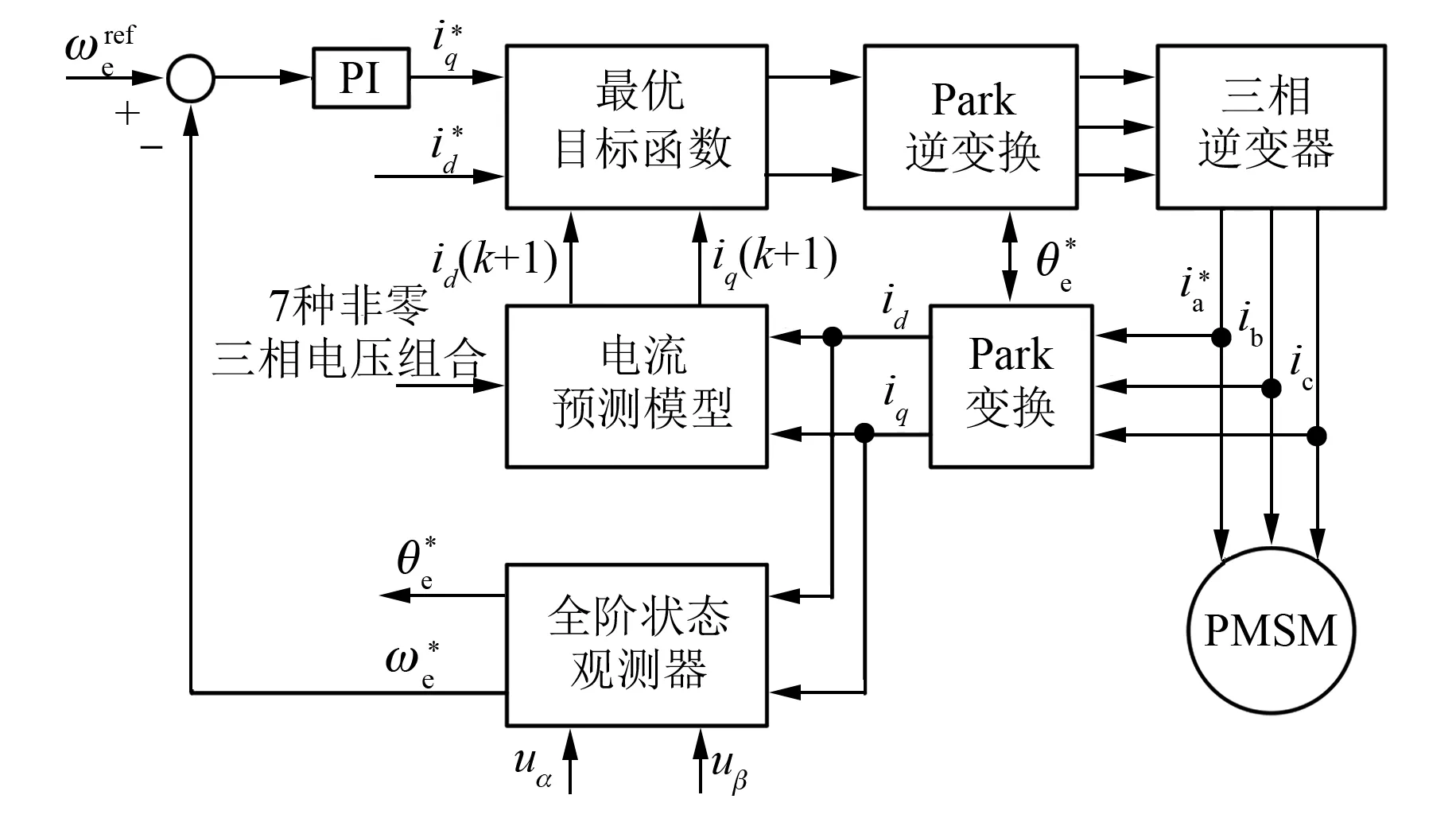
图5 基于全阶状态滑模观测器的PMSM MPCC原理图

3.1 2种观测器观测精度仿真分析

电机参考给定转速为1 500 r/min，传统观测方法和全阶状态滑模观测方法下的电机转子位置和角度仿真波形如图6所示。

图6 电机转子位置和角度仿真波形

通过比较图6(a)、图6(b)可以看出，传统观测器在观测电机转子角度位置时，0.04 s时才能稳定；而全阶状态滑模观测器在观测电机转子角度位置时，0.02 s时即可准确跟踪电机转子实际角度位置，且在观测过程中，观测曲线稳定性好，几乎没有波动。

由此可以验证，加入了模糊控制的思想的全阶状态滑模观测器可以快速、准确地观测电机转子角度位置。

3.2 电机动态特性仿真分析

电机空载起动至参考给定转速1 500 r/min，在0.6 s时给电机加载到8 N·m，稳定运行至1.4 s时，给电机减载到4 N·m，所得电机定子电流、转速和转矩仿真波形如图7～图9所示。

图7 电机定子电流仿真波形

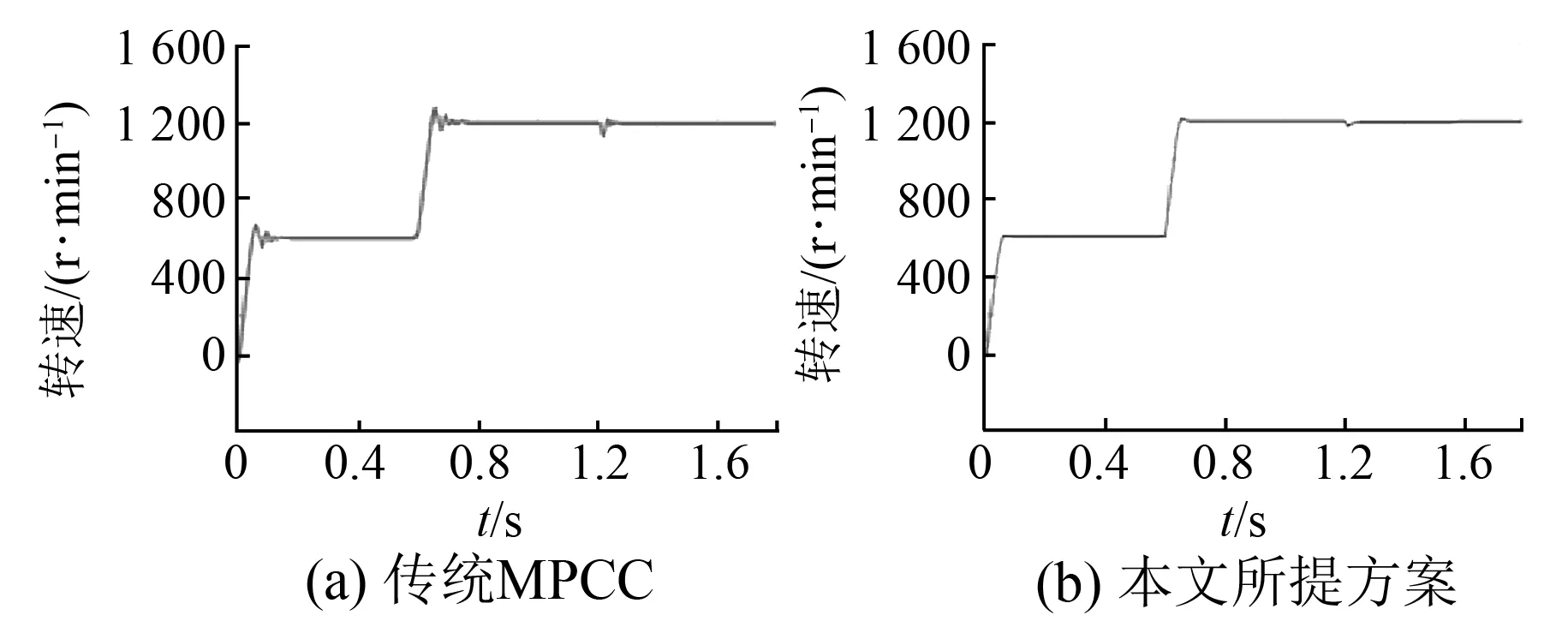
图8 电机转速仿真波形

图9 电机转矩仿真波形

对比图7(a)、图7(b)可以看出，本文所提控制策略下的电机定子电流超调量小，稳定性能好。

对比图8(a)、图8(b)可以看出，传统MPCC下的电机转速存在一定程度的超调，且调节时间较长。而本文所提控制策略下的电机转速几乎没有超调，且调节时间明显缩短。由此证明了，本文所提出的控制策略具有良好的电机调速性能。

从图9(a)、图9(b)可以看出，与传统MPCC相比，本文所提控制策略下的电机转矩更加平稳，波动更小。

4 结 语

本文提出一种基于全阶状态滑模观测器的PMSM MPCC方案，能够降低电压矢量选择时的计算量，提高运算效率。同时，能够对PMSM的转子位置和转速进行精准估算，消除了观测过程中存在的转子位置和转速抖振问题，提高了PMSM的控制性能。