动平衡机气体驱动研究

2021-04-23王贺权马星宇曲天羽

液压与气动 2021年4期

王贺权，马星宇，曲天羽

(1.沈阳航空航天大学机电工程学院，辽宁沈阳 110136； 2.凤城市时代龙增压器制造有限公司，辽宁凤城 118100)

引言

动平衡是涡轮增压器转子生产和制造必不可少的重要环节，其检测的精确程度直接影响旋转机械的性能和寿命[1]。因此只有精确地测量转子不平衡量，使其数值在许用范围内，才能保证转子良好的工作性能。

在实际工作中，对于平衡机精度的影响因素很多，最主要的影响因素之一是驱动系统。动平衡机的驱动系统可以分为：万向节驱动系统、带圈驱动系统、气体驱动等。万向节驱动为刚性接触性传动，对转子不平衡量测量的精度影响很大；带圈驱动虽然是柔性接触，但仍会对动平衡机产生波动性影响[2]；气体驱动为非接触式驱动，具有驱动平稳，功率小等优点，特别适用于带叶片类转子[3]。

对于动平衡机驱动系统的研究，国内外学者开展了大量的研究工作。万勇等[4]优化了喷嘴并实现流量的精确控制。石凯凯等[5]分析了喷嘴位置对压气机叶轮旋转的影响。王秋晓等[6-7]分析了动平衡机摆架系统扭摆效应所造成的测量误差。SU等[8]提出了新型自动动平衡驱动器。BECZE等[9]对涡轮增压器平衡机的气流驱动与转速进行分析和优化。李皓月等[10]研究了平衡机和转子叠加引起的转子振动中心的变化问题。QIN等[11]在一定的旋转频率范围内，采用频率补偿方法得到了优于标称频率响应特性的补偿结果。虞启辉等[12]分析了进气压力与转速的关系。郑恒等[13]分析了气动马达流场状态，并对其进行优化。郜思洋[14]设计了气悬浮盘式转子动平衡机并研究了气驱动技术。目前主流研究是采用万向节驱动、带圈驱动和垂直放置涡轮转子气体驱动，而针对水平放置的涡轮转子气体驱动的研究却少见报道。

本研究应用气体驱动系统，确定了水平放置涡轮转子在动平衡检测中的转速与气体流量的关系，根据实验分析了气体驱动系统对不平衡量测量的干扰；并研究了不同驱动方式、不同转速对转子振动中心的影响及不同试重下不平衡量的误差。

1 结构参数

1.1 结构设计

气体从喷嘴孔喷出，作用于涡轮转子叶片驱动其旋转。在此工作过程中，若没有外壳对气流进行导向，则气流的大部分动能会浪费。因此，设计了一种涡轮罩壳，使高速气流以一定的角度喷射在叶片上，驱动涡轮转子旋转做功。涡轮罩壳的示意图和实物图如图1所示，通过控制进入喷嘴气体的流量的大小，来控制涡轮转子的转速。

图1 涡轮罩壳与测量转子

1.2 关键尺寸设计

气体驱动涡轮转子旋转类似于废气从叶栅流出驱动涡轮。为了减少气流扰动对动平衡机有用信号的干扰，喷嘴仅布置在垂直于摆架的振动方向上。如图2a所示，气流出口角α1b和喷嘴出口位置与气流作用于叶片位置的距离，决定了涡轮转子的圆周速度，从喷嘴出来的实际气流是偏离气流出口角α1b的,而精确的实际气流角度α1通常由公式(1)得出[15]：

(1)

式中，a—— 出口最小宽度

t—— 出口最大宽度

在应用中用a值控制α1角的大小。而实际出口角α1取值范围在20°～22°。涡轮转子在测量前会有一定的偏心距，为了防止涡轮转子振动时撞击内壁，涡流罩壳内径与叶轮之间应有一定间隙如图2b所示，即：

DN=D1+2Δ

(2)

Δ=(0.04～0.08)D1

(3)

式中，DN—— 涡轮罩壳内径

D1—— 所选用涡轮转子叶片外径

Δ —— 轮壳间隙

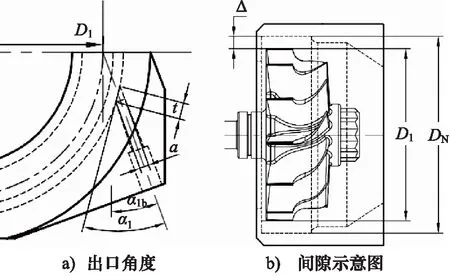
图2 结构示意图

2 数学模型

气体作为驱动力时通过喷嘴流向涡轮叶片，并以一定的角度α1射入涡轮的叶片之间。气体作用在叶片的冲击力对涡轮转子产生转动力矩，并克服阻力矩使涡轮转子转动[1]。当入射角度和喷嘴出口位置确定后，转子的转速仅与通过喷嘴的流量有关。

在转速平稳的条件下，流经涡轮转子的流量qv与涡轮转子旋转的角速度ω呈线性关系，可表示为ω=Cqv。而实际测量时，系数C值并不是保持不变的，与流体在叶道中的流动状态有关，从而产生误差[13]。要使驱动系统正常工作，需要涡轮转子保持稳定的转速，根据C与qv的函数关系C=f(qv),建立相关的数学模型，根据运动学定律得出：

(4)

式中，J—— 涡轮转子的转动惯量

Tr—— 气体通过涡轮时对叶片的推动力矩

Tf—— 摩擦阻力力矩

Ta—— 气体通过涡轮叶片时对涡轮转子产生的流动阻力矩

当涡轮转子转速达到测量值时，涡轮转子角速度处于稳定状态，即角加速度为0，此时通过涡轮转子叶片的流量为定值，得：

Tr=Tf+Ta

(5)

根据流体在旋转机械中的流动原理，动量矩方程适用于流体在涡轮叶片中作定常流动。因此由动量矩定理可以得出各质点力矩和∑M为:

(6)

(7)

将式(7)代入式(6)中，得:

(8)

由作用力和反作用力的关系，气流对叶片的转矩与叶片对气流的转矩相反，所以气流对叶片的作用力为：

(9)

图3 通过叶轮流体速度示意图

如图3所示，入口速度与入口流量的关系为c1u=η1qv/s；出口速度与圆周速度的三角关系为c2u+u2=w2u；其中w2u=ηωr2；u2=ωr2,所以整理为c2u=η2ωr2。将上述关系式代入式(9)中，推得流量、转速、力矩的表现形式为：

(10)

式中，η1—— 流量从喷嘴流向叶片的损失系数

η2—— 圆周转速与出口速度的相关系数

ρ—— 气体密度

r1，r2—— 分别为叶轮入口直径和出口直径

S—— 喷嘴出口横截面积

c1u—— 气体流向叶片的绝对速度在圆周速度上的投影

c2u—— 出口气流绝对速度在圆周速度上的投影

转子的转速由0至匀速转动的过程中，只分析转子未发生旋转和保持匀速转动的两种状态，当气流产生的转矩小于摩擦阻力矩时，转速ω=0,且流动阻力矩Ta=0，将参数代入式(5)、式(10)联立的式子中，得最小启动流量qmin为:

(11)

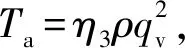
(12)

根据比例系数C和最小启动流量qmin构造一元一次函数，所以流量与转速的最终表达式为:

ω=C(qv-qmin)

(13)

由上式可以看出，流量与转速呈正比关系，斜率主要与涡轮进出口半径和喷嘴横截面积有关。

3 实验研究分析

3.1 实验装置

动平衡驱动系统的主要性能指标是驱动转速的稳定性和有足够的功率使工件驱动至所需平衡转速的能力。实验主要对动平衡机驱动系统进行实验验证和分析，研究转速与流量的关系，并对比气体驱动与带圈驱动对测量结果的不同影响。气体驱动动平衡机实验装置如图4所示，表1为实验参数。

3.2 流量与转速关系实验

当转子具有气动外形，就可以用气体作为驱动源驱动转子旋转。图5为不同的启动阻力矩下测量流量与转速的关系。

图5中反映了流量与转速的线性关系，随着阻力矩的增大，最小启动流量也随之增大，但是实验转速随

图4 气体驱动动平衡机实验装置图

表1 动平衡实验参数

流量增大的幅度没有理论幅度大，可能是因为理论公式无法将所有影响条件代入作为参数，例如转速流量的测量精度。相同条件下，参数的理论曲线与实际结果变化趋势基本一致。

在有无外壳对比实验中，喷嘴位置相同并在一定的流量范围内，无壳条件下，流量与转速也保持了线性关系。有壁的自由射流与无壁的自由射流是两种不同的流动状态，无壳气体驱动转子的最小启动流量明显大于有壳气体驱动的最小启动流量，并且有壳气体驱动可以充分利用高速气流的动能，使转子具有更好的驱动响应。

3.3 转速波动实验

转子的振动中心与转速有关，而转速的波动会使转子的振动中心改变，从而影响测量的最终结果。根据不平衡转子的运动规律可知，y0为随质心的平动，α为绕质心的摆动，所以振动中心到质心的距离L可表示为y0与α的比值；ξ为转速波动对振动中心影响误差。

(14)

(15)

式中，ω—— 转速

z—— 不平衡质量到质心的距离

M—— 振动系统的质量

JT—— 转动惯量

ωα—— 绕质心转动的固有频率

ωy—— 平动的固有频率

ω1，ω2—— 分别为测定转速中出现的最高转速和最低转速

L1，L2—— 分别为最高转速和最低转速对应的距离

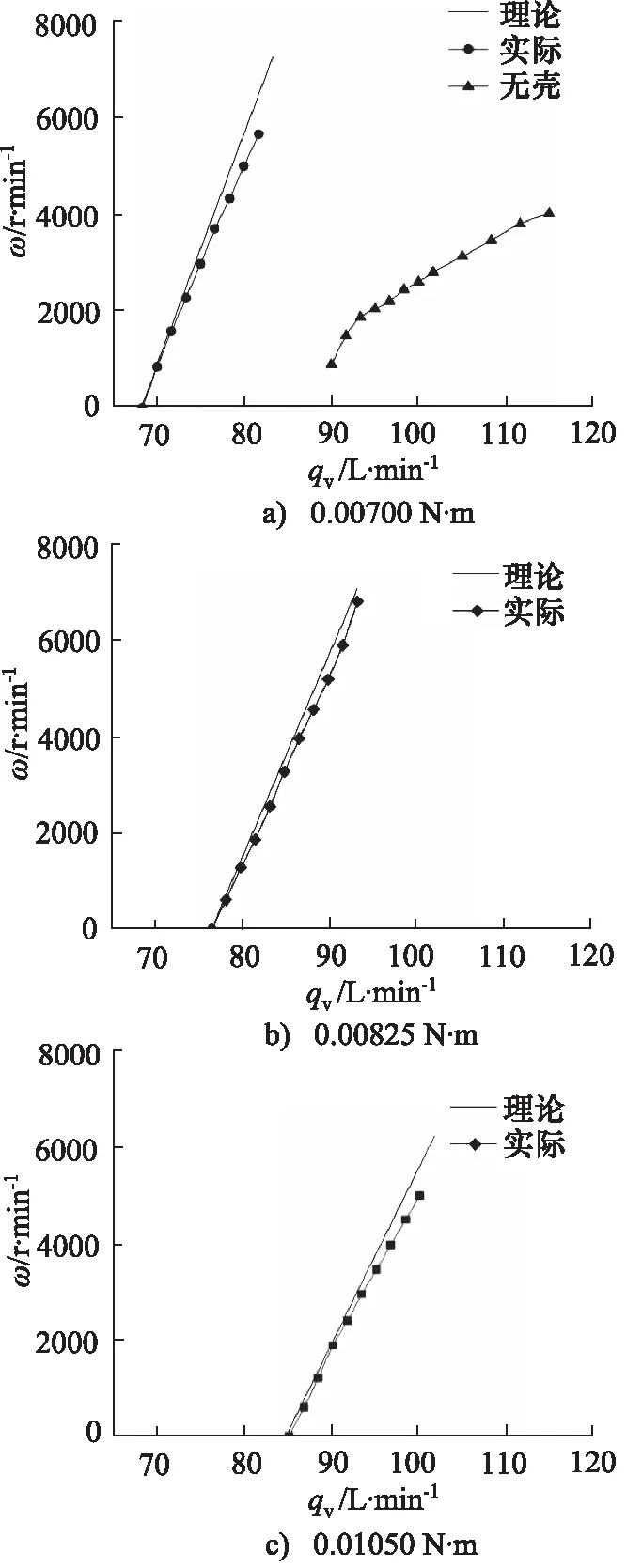
图5 不同阻力矩下流量与转速关系图

对于软支承动平衡机，转速频率为系统固有频率的2.5倍，可认定为趋近于振动中心的极限值[3]。ξ越小说明转速波动对振动中心位置的影响就越小。动平衡机的固有频率为1500 Hz。选择四种测量转速值，维持电机转速与气体流量保持一定值不变，测量涡

图6 转速波动图

轮转子的波动情况，经过加速阶段后，记录40 s内每一次转速变化的数值，测量次数n，如图6所示。

将带圈驱动和气体驱动的转速最大值和最小值代入式(15),得出不同转速下转速波动对振动中心影响误差如图7所示。当转速达到2.5倍的固有频率以上，转速波动对振动中心的影响较小。测量了转速稳定后的20组数值，并分析数据的均方误差如表2所示，并将标准差σ绘制在图7中。通过综合分析，在5000 r/min下，测得的转子转速更趋近于稳定转速；

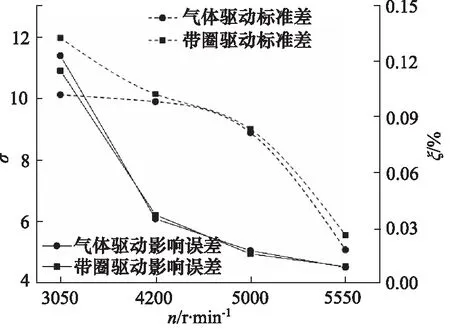
图7 气体驱动与带圈驱动的标准误差与影响误差

表2 转速波动均方误差

相对于带圈驱动，气体驱动转速波动更小，进而对振动中心的影响也越小。

3.4 气体驱动与带圈驱动的不平衡量对比

为对比气体驱动与带圈驱动的测量精度，选用由气悬浮测量方式精确平衡的标准涡轮转子。将同一状态下的转子分别在两种驱动方式下进行动平衡检测，添加相同的质量，在左右校正面添加方式如表3所示,并通过测量得到如表4、表5所示数据，通过对比可知，在小于350 mg试重以下，相位角偏差均未大于10°，因此忽略影响。