基于多轴电液伺服转向系统的重型车辆操纵稳定性研究
2021-04-23)
)
(福州大学 机械工程及自动化学院, 福建 福州 350108)
引言
重型车辆广泛应用于基础设施建设,如大吨位全路面起重机、大型运梁车和矿用自卸车等民用装备;及军事重工领域,如大型导弹运输车、重型电子发射车和牵引运载车等军用特种车辆[1-2]。同时,由于单轴承重的限制并考虑到道路损坏,常通过增加重型车辆的轴数提高其运输效率[3]。然而,多轴车辆由于整车尺寸和承载质量增大以及工况的复杂, 转向时机动性变差, 驾驶员操作困难,容易引发安全事故。因此有必要深入研究多轴车辆的操纵稳定性。
为了分析多轴车辆转向时的操纵稳定性,建立准确的操纵动力学模型成为横向动力学研究中的重点,许多学者对此已经做了不少工作。ELLIS[4]以前轮转向的三轴车辆为研究对象,提出了将不参与转向的后两轴等同为位于其中间位置的单个等效轴,在假设所有轮胎都具有相同的侧偏刚度且各轴载荷平均分配的前提下,将三轴车辆等效为二轴,对原有二自由度自行车模型进行扩展。但该模型的侧偏角只与侧向加速度有关,WINKLER等[5]进一步研究了轮胎侧偏角与车速、转弯半径等的关系,对具有多个非转向轴的重型卡车建立了轮胎侧偏角与转弯半径及侧向加速度的函数,提出了一种更为复杂的通用车辆操纵稳定性分析模型。上述模型针对的是前轴转向的车辆。接着,人们研究了多轴转向的操纵稳定性。李运华等[6]针对非完整约束多轴驱动车辆,以中间轴为基准建立动力学模型。QU Q等[7]建立了前后轴转向的三轴车辆模型,基于人-车-路闭环系统,通过后轮转向提高车辆的操纵稳定性。BAYAR K[8]将四轮转向系统转向策略推广到多轴,建立了可以实现全轮转向的三、四轴车辆模型。WILLIAMS[9]通过对已建立的二轴和三轴模型进行改进并推广到n轴,建立了一个具有任意转向轴的多轴车辆二自由度通用动力学模型。上述研究所建立的二自由度动力学模型都是以前轮转角为输入。然而,在重型多轴车辆中,由于车轮惯量大和电液伺服转向系统固有频率低,转向系统的响应速度并不快。因此,转向系统成为影响重型多轴车辆操纵稳定性的重要因素[10]。为此,需结合转向系统模型以进一步分析其对重型车辆操纵稳定性的影响。
对于重型多轴车辆,其负载大、变化范围广、转向模式多样,为保证车辆的越野性和灵活性,重型多轴车辆通常采用电液伺服转向系统。DU H等[2]针对实际多轴车辆建立了包含转向机构和液压系统的单轴电液伺服转向系统非线性时域模型,并进行了试验验证。基于此模型,本研究以七轴电液伺服转向车辆为例对线性二自由度模型扩展,建立了考虑转向系统影响的多轴电液助力式二自由度动力学模型。接着,以横摆角速度和质心侧偏角为评价参数对模型进行仿真分析,研究转向系统对整车操纵稳定性的影响及不同转速、转角输入下的影响规律。
首先,建立电液伺服转向系统模型及多轴转向车辆线性二自由度动力学模型;其次,基于MATLAB/Simulink软件,建立多轴电液助力式转向车辆动力学仿真模型,研究电液伺服转向系统对多轴车辆操纵稳定性的影响,并分析不同车速和转角输入下的质心侧偏角和横摆角速度响应;最后,对本研究内容进行总结和展望。
1 多轴电液助力式转向车辆线性二自由度动力学模型
重型多轴车辆转向系统中,各转向轴大都采用电液伺服转向系统,且各轴相互独立以实现多模式转向。因此,为建立多轴转向车辆线性二自由度动力学模型,首先需要建立单轴转向系统模型,在此基础上根据多轴转向动力学关系将各转向轴组合,建立包含转向系统的多轴车辆线性二自由度动力学模型。
1.1 电液伺服转向系统动力学模型
电液伺服转向包含两部分:机械系统和液压系统,如图1所示。机械系统由梯形机构(包括左右转向节臂、横拉杆以及横梁)、左右轮胎等组成。液压系统是由伺服比例阀、双转向助力缸、角位移传感器等元件组成。转向系统通过左右转向助力缸带动梯形机构运动,从而实现轮胎的转向。电液伺服转向系统的液压控制系统是由1个伺服比例阀控制2个串接的转向助力缸实现液压系统驱动和控制。电液伺服转向系统的详细信息已在之前研究中进行详细描述[2],所以此部分不对系统机械模型和液压模型进行赘述,只给出推导结果。

1.轮胎 2.横向拉杆 3.转向节臂 4.转向助力缸 5.车桥 6.转向节 7.伺服比例阀图1 电液伺服转向系统示意图
1) 电液伺服转向系统机械模型
如图1所示,设右侧轮胎绕主销转动的转角为β,左侧为α,以右侧转角为自变量。建立电液伺服转向系统机械部分动力学方程[2]:

(1)

θ3—— 右侧转向助力缸作用力与作用点速度的夹角
JL,JR—— 左、右侧轮胎及其附属结构绕右侧主销转动的等效转动惯量
CL,CR—— 左、右侧轮胎等结构的等效阻尼系数
TL,TR—— 左、右轮转向阻力矩
FL,FR—— 左、右缸转向助力
2) 电液伺服转向系统液压模型
通过推导,可以获得电液伺服转向系统的液压模型[2]。左右转向助力缸驱动力:
(2)
式中,p1,p2—— 分别为伺服比例阀A,B口压力
a—— 转向助力缸有杆腔的面积
A—— 转向助力缸无杆腔面积
伺服比例阀可以看作是理想零开口四边滑阀,其阀口流量方程为:
(3)
式中,q1—— 流入两转向助力缸的流量
q2—— 流出两转向助力缸的流量
xv—— 伺服比例阀的开口量,并规定阀芯向左移为正方向
Cd—— 伺服比例阀各节流口的流量系数
w1,w2—— 滑阀面积梯度
双转向助力缸的流量连续性方程为:

(4)
式中,Cip—— 转向助力缸内泄漏系数
Cep—— 转向助力缸外泄漏系数
Vt—— 有杆腔和无杆腔的总容积
xL,xR—— 左右转向助力缸活塞位移
1.2 多轴转向车辆线性二自由度动力学模型
为建立各转向轴之间的运动学关系、研究多轴转向车辆的操纵稳定性,参考车辆动力学及控制、汽车理论等[11-20],建立七轴全地面起重机的转向运动二自由度动力学模型。提出理想化的假设:
(1) 忽略悬架作用,认为车辆只做平行于地面的平面运动,即忽略车辆沿Z轴的位移、绕Y轴的俯仰角及绕X轴的侧倾角;
(2) 假定汽车的前进速度u不变;
(3) 汽车侧向加速度限定在0.4g以下,轮胎侧偏特性处于线性范围;
(4) 忽略空气动力学影响,忽略左右轮载荷变化引起的轮胎特性变化。
因此,认为车辆只有沿Y轴的侧向运动与绕Z轴的横摆运动两个自由度,多轴车辆转向动力学模型如图2所示。

图2 多轴转向车辆线性二自由度动力学模型
由图2可知,以各轮转角为输入,二自由度车辆受到的外力沿Y轴方向的合力与绕质心的力矩和为:
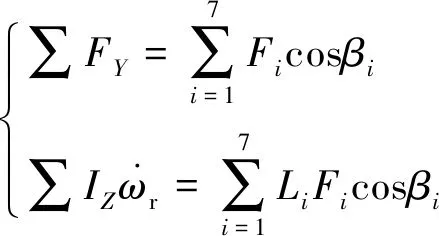
(5)

式中,FY—— 车辆沿Y轴方向的合力
IZ—— 绕Z轴的转动惯量
ωr—— 横摆角速度
M—— 整车质量
Fi—— 第i轴轮胎受到的侧偏力(N),
Fi=ki×φi
ki—— 第i轴轮胎侧偏刚度之和
φi—— 第i轴轮胎的侧偏角
βi—— 车辆第i轴右轮转角
Li—— 质心到第i轴的距离(m),在质心之前为正,质心之后为负
考虑到βi角较小,cosβi=1,式(5)可写作:
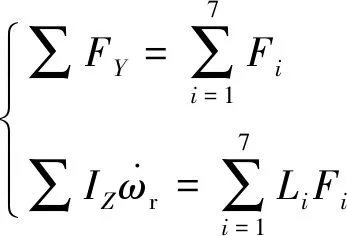
(6)
车辆各轴侧偏角与其运动参数有关。如图2所示,车辆各轴中点速度为ui,质心侧偏角为δ,δ=v/u。ξi是ui与X轴的夹角,其值为:
(7)
前后轮侧偏角为:
(8)
式中,v—— 车辆质心处的侧向速度
u—— 车辆质心处的纵向速度
ξi—— 车辆第i轴轮胎的航向角
因此,外力、外力矩与汽车运动参数的关系式为:

(9)
整理得多轴车辆二自由度微分方程为:
根据Ackermann转向定理:
(11)
式中,li—— 各轴到瞬心的距离在X轴的投影,
li=Li-D
D—— 质心到瞬心的距离(向X方向为正)
考虑到转角βi较小,近似处理后得到:
(12)

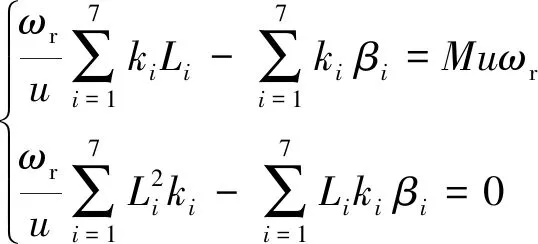
(13)
将式(12)代入式(13)中,化简得到质心到瞬心的距离D:
将式(14)代入式(10)中,并写成状态空间方程形式:


(15)
写成状态空间方程:

(16)
其中:
x=[δωr]T;U=[β1…β7]T;


2 多轴电液助力式转向车辆操纵动力学仿真分析
通过多轴转向车辆线性二自由度动力学模型,获得多轴车辆各转向轴之间的转角关系将单轴电液伺服转向系统扩展到多轴,建立包含转向系统的多轴电液助力式转向线性二自由度动力学模型,如图3所示。
驾驶员给转向盘一个转角信号, 通过质心零侧偏角控制策略,算得各转向轴理论转角后通过电液转向系统控制轮胎转向。电液伺服转向系统模型如图4所示,电液伺服转向系统相关设计变量值如表1所示。
为评价转向盘角阶跃输入下的转向特性,以质心侧偏角和横摆角速度的瞬态响应作为评价参数,研究电液伺服转向系统对整车操纵稳定性的影响,并讨论转角输入及车速对二自由度模型操纵稳定性的影响。质心侧偏角为车辆纵向平面与运动方向的夹角,质心侧偏角越小,车辆遵循驾驶者指令按照给定方向行驶能力越好;横摆角速度为车辆围绕车身坐标系中垂向轴转动的角速度,为保证车辆的操纵稳定性,低速时应使横摆角速度响应快、横摆角速度增益大一些,高速时相反。

图3 多轴电液助力转向车辆Simulink模型

图4 电液伺服转向系统模型
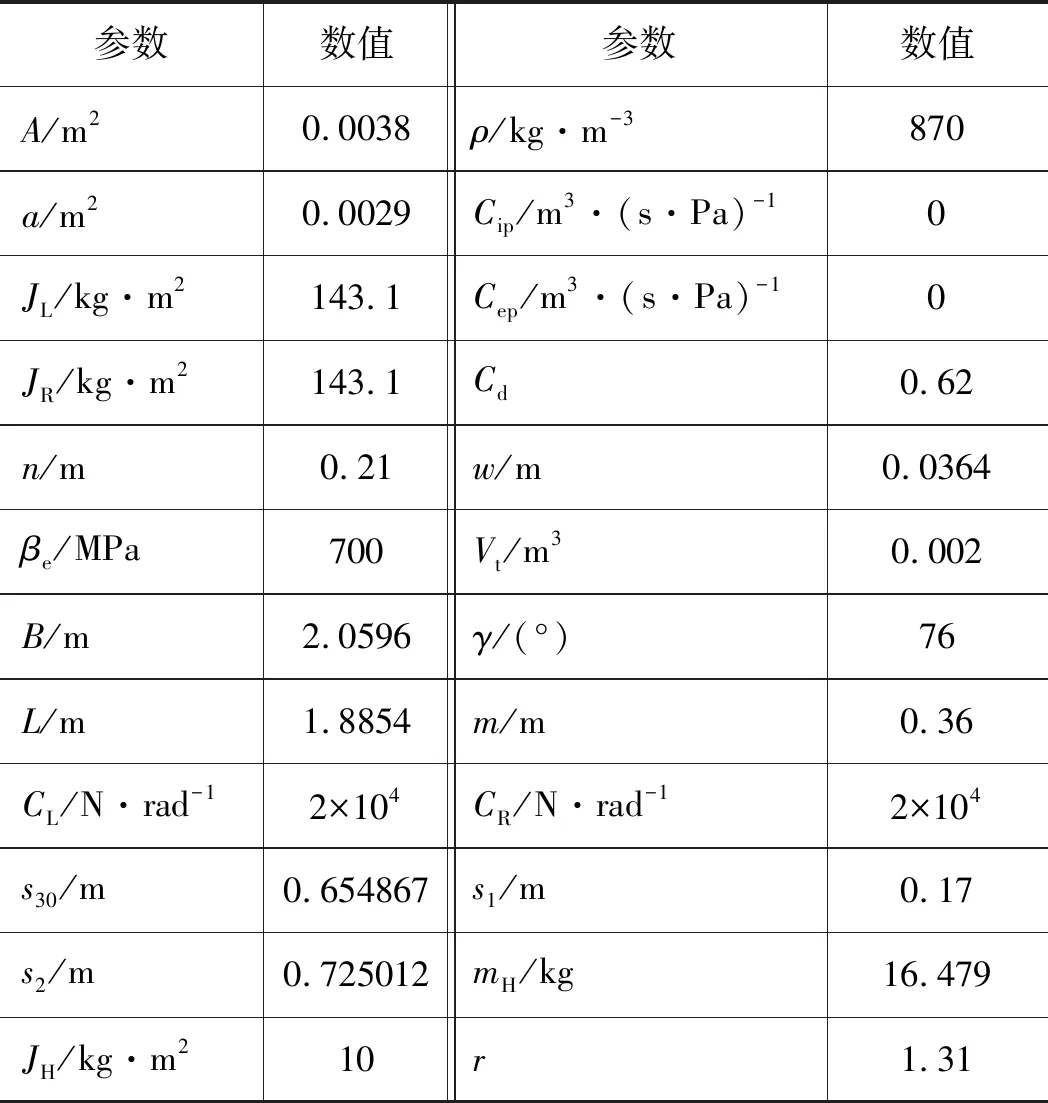
表1 电液伺服转向系统的相关设计变量值
2.1 有无转向系统的二自由度模型仿真
为研究电液伺服转向系统对整车操纵稳定性的影响,在车速为20 km/h给转向盘15°的阶跃信号,与无转向系统的线性二自由度动力学模型对比,图5为相应的车辆质心侧偏角和横摆角速度响应。
二者都是基于质心零侧偏角控制策略,因此稳态时质心侧偏角都为0,如图5a所示。考虑电液伺服转向系统的二自由度模型质心侧偏角瞬态峰值明显下降,意味着在该行驶条件车辆服从驾驶者指令、沿指定弯道行驶而不发生偏离的能力更好;图5a中电液伺服转向系统使车辆的横摆角速度响应变慢。上述结果都显示了电液伺服转向系统使多轴车辆到达稳态转向的时间增加了0.8 s左右,这主要与重型多轴转向系统频宽低及重型车辆惯性大等因素有关。
2.2 不同转角输入下的横摆角与质心侧偏角
进一步地,分析不同转角输入工况下电液伺服转向系统对整车操纵稳定性的影响。图6所示为车速10 km/h,转角输入分别为5°,15°,25°时车辆质心侧偏角与横摆角速度响应。
2.3 不同车速下的横摆角速度与质心侧偏角
为分析电液伺服转向系统对整车操纵稳定性的影响与车速的关系,图7为转向盘转角输入为5°,行驶车速分别为10, 20, 30 km/h, 多轴转向车辆的质心侧

图5 两种模型质心侧偏角与横摆角速度响应
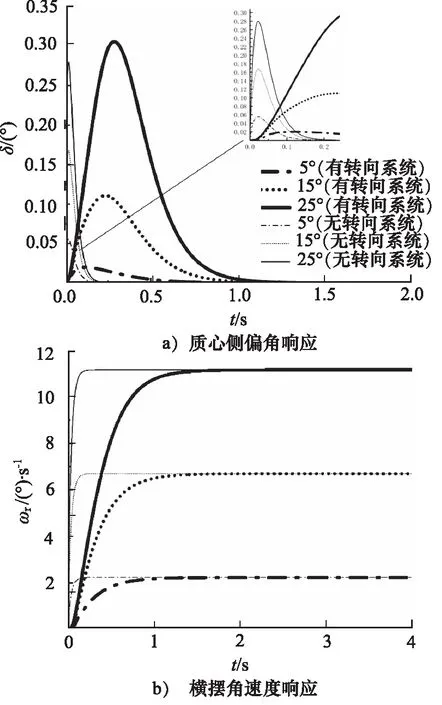
图6 不同转角输入下的多轴车辆转向特性

图7 不同车速下的多轴车辆转向特性
偏角与横摆角速度响应。
首先对不同因素对质心侧偏角响应的影响规律进行分析,如转角和车速。图6a中,相同车速工况下,转角较小时,有转向系统模型时质心侧偏角小于无转向系统模型的质心侧偏角;而值得注意的是,在大转角工况下,有转向系统模型时质心侧偏角超过了无转向系统模型的质心侧偏角。图7b中,在相同转角工况下,随着车速增加,有转向系统的模型和无转向系统模型的质心侧偏角峰值均增加,同时有转向系统模型的质心侧偏角峰值小于无转向系统模型。因此,在高速小转角下,有转向系统的质心侧偏角低于无转向系统。而不同因素对横摆角速度响应的影响,如图6b和图7b所示。有转向系统的模型横摆角速度响应都比无转向系统模型滞后,这个滞后的程度随着转角增加越明显,随着车速的增加却无明显变化。这是由于转向系统模型是非线性的,转角变化时转向系统的非线性模型对整车的动态特性影响更明显,而整车二自由度模型是线性的,车速变化对动态特性的影响不明显。
3 结论
基于广义多轴转向车辆动力学方程,分析了各轴转向运动学关系,并联立各轴单轴电液伺服转向模型,建立了多轴电液助力式转向车辆二自由度动力学模型,并对系统的质心侧偏角和横摆角速度规律进行了分析。结果表明:在小转角范围内,有转向系统模型时的质心侧偏角普遍小于无转向系统模型时的质心侧偏角;同时,随着车速增加,有转向系统的模型和无转向系统模型的质心侧偏角峰值均增加;有转向系统的模型横摆角速度响应都比无转向系统模型滞后,该滞后程度随转角增加越明显,但随车速增加无明显变化。
