双喷嘴挡板力反馈两级电液伺服阀的物理建模

李跃松

(河南科技大学 机电工程学院， 河南 洛阳 471003)

引言

双喷嘴挡板力反馈两级电液伺服阀线性度好，动态性能好，受温差变化影响较小，是目前国内应用最广泛的一种电液伺服阀[1-2]；但由于其涉及机械、电子、磁场、流体传动、传感和控制等技术，描述其工作机理的数学模型十分复杂且不便于分析和仿真计算。在工程应用中往往采用便于分析的线性化模型，而线性化模型是简化模型，只有在一定的限制条件下才准确，因此获得一种准确简单的电液伺服阀建模方法对于电液伺服阀的准确应用十分重要[3-6]。

随着计算机软件的发展，物理建模方法被越来越多的工程应用者所青睐。物理建模方法只需通过将基础组件依照原理图对物理组件的模块框图连接装配，就可以建立复杂的多学科领域的系统模型， 并在此基础上进行仿真计算和深入分析，从而避免繁琐的数学建模[7-8]。本研究将基于Simulink物理建模工具箱给出双喷嘴挡板电液伺服阀物理建模方法，并给出其稳态和动态性能。

1 双喷嘴挡板电液伺服阀

双喷嘴挡板力反馈两级电液伺服阀结构，如图1所示[9]。其前置级液压放大器为双喷嘴挡板阀，由永磁动铁式力矩马达控制，第二级液压放大器为四通滑阀，阀芯位移通过反馈杆与衔铁挡板组件相连，构成滑阀位移力反馈回路。

1.衔铁 2.挡板 3.阀芯 4.上导磁体 5.下导磁体 6.喷嘴 7.固定节流孔图1 双喷嘴挡板力反馈两级电液伺服阀

当无电流输入时，衔铁处在上、下导磁铁中间位置，挡板处在2个喷嘴中间位置，阀芯在反馈杆小球的约束下处于中位，滑阀无液压能输出。当有电流输入时，衔铁在电磁力矩作用下，带动挡板组件发生偏转，喷嘴与挡板构成的液阻发生变化，致使阀芯两端腔内压力发生变化，驱动阀芯运动，阀芯带动反馈杆变形，当反馈杆对衔铁的作用力与其所受电磁力相平衡时，阀芯停止。输出与控制电流成比例的流量。

2 双喷嘴挡板电液伺服阀物理模型

2.1 力矩马达

由图1中力矩马达结构图，可建立如图2所示的磁路简图，Simulink磁路元件如表1所示。

图2 力矩马达磁路简图

表1 Simulink磁路物理建模元件

2.2 液压放大器

双喷嘴挡板液压放大器由喷嘴、固定节流孔和挡板构成。挡板和两喷嘴间的柱面构成2个可变节流孔，其通流面积有挡板位移改变。

由图1双喷嘴挡板液压放大器的结构和表2所示节流孔的物理模型可得，双喷嘴挡板液压放大器的物理模型如图3所示。

图3 双喷嘴挡板液压放大器物理模型

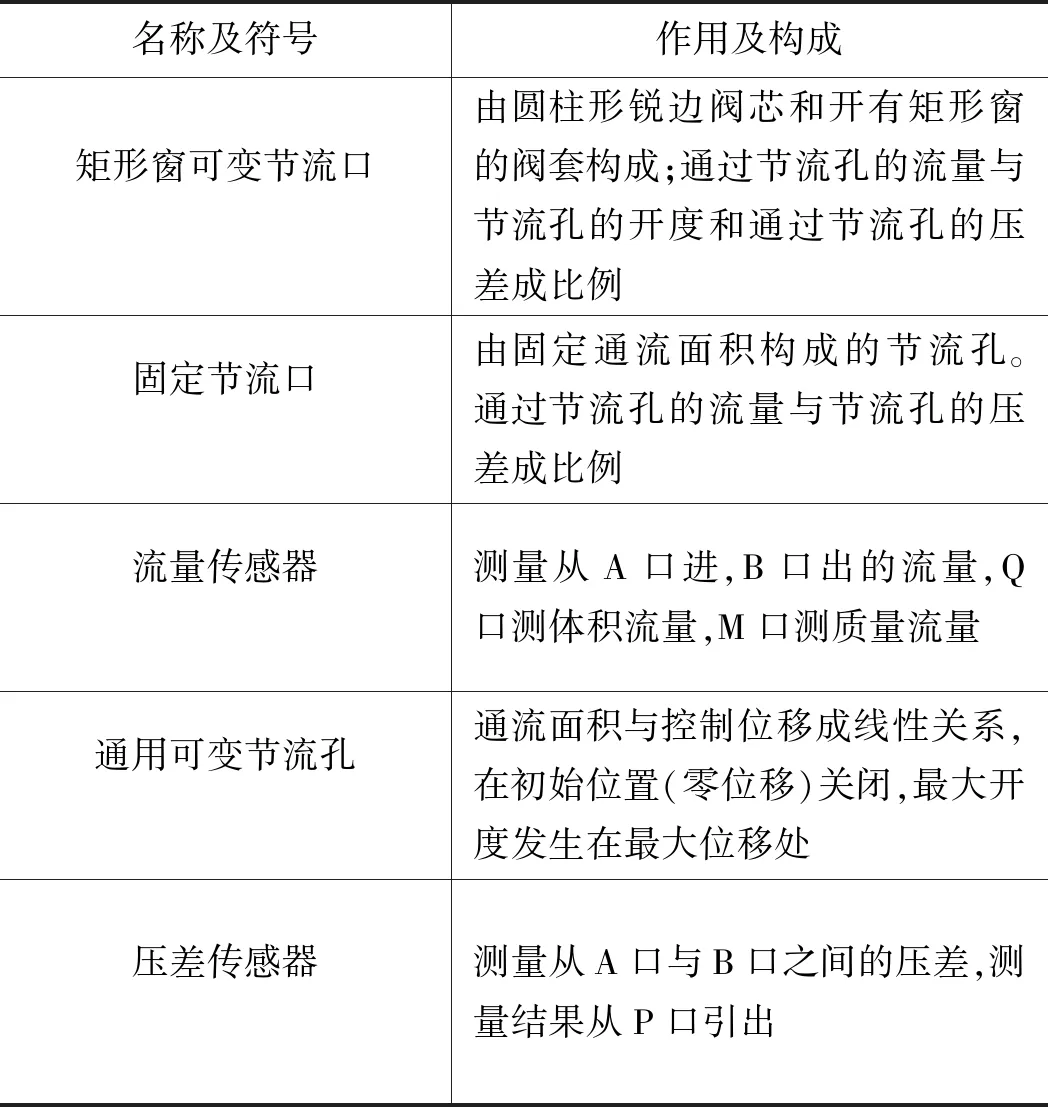
表2 Simulink液压节流元件物理模型

两级伺服阀常用滑阀液压放大器为四通圆柱滑阀，其结构如图4所示。其液压能控制分别通过4个可变矩形窗节流孔完成，4个节流孔分别为PA、AT、PB和BT。可变节流孔通流面积由阀芯位移改变。由滑阀结构原理和表2可得， 滑阀液压放大器的物理模型如图5所示。

图4 滑阀液压放大器结构原理

2.3 双喷嘴挡板电液伺服阀

由上所述及图1可得，双喷嘴挡板力反馈两级电液伺服阀的物理模型如图6所示。其中反馈杆具有弹簧特性和阻尼特性可以等效为反馈弹簧和反馈阻尼[6]。

图5 滑阀液压放大器物理模型

图6 双喷嘴挡板力反馈两级电液伺服阀物理模型

3 仿真分析

取供油压力21 MPa，固定节流口直径0.2 mm，喷嘴直径0.42 mm，喷嘴挡板零位间距为30 μm，代入图3，可得双喷嘴挡板液压放大器的压力特性曲线如图7所示。

图7 双喷嘴挡板液压放大器压力特性曲线

由图7可知，挡板在-30～30 μm运动时，压力变化范围为-16.85～16.85 MPa。取挡板运动区间[-1 μm,1 μm]内的压力灵敏度近似为零位压力灵敏度，由图7可知挡板运动范围为-1～1 μm时的压力灵敏度为0.6998 MPa/μm，采用理论公式计算的零位压力灵敏度取值0.7 MPa/μm，两者之间十分接近，可见双喷嘴挡板液压放大器物理模型准确度较高。

下面对双喷嘴挡板力反馈两级电液伺服阀的静、动态特性进行仿真。为便于对比和验证，仿真参数取参考文献[10]所给参数，此参数与额定流量为15 L/min的MOOG 31伺服阀结构参数接近，将结构参数代入图6物理模型。

取控制电流幅度为10 mA，驱动频率为0.01 Hz，可得所仿真伺服阀的空载流量特性曲线如图8所示。

图8 空载流量特性曲线

由图8可知，所仿真伺服阀在-10～10 mA变化时，空载输出流量-15～15 L/min。与参考文献[11]所给设计值和MOOG 31伺服阀的所对应额定流量取值一致。

将图7中，正弦信号换成阶跃信号，幅度为10 mA，仿真可得伺服阀的时域特性曲线如图9所示。由图9可知，在供油压力为21 MPa，仿真伺服阀的上升时间约为3 ms，稳态调节时间7 ms。而相同条件下，MOOG 31伺服阀样本所给上升时间为2.5 ms，稍快于物理模型仿真结果。

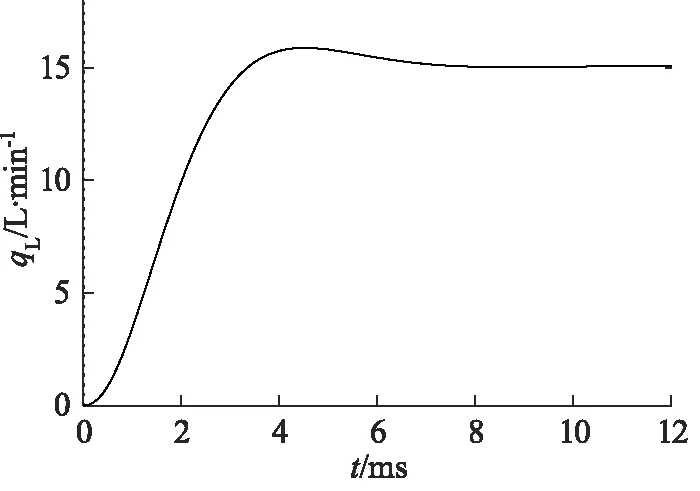
图9 额定输出下的阶跃响应曲线

令图7输入信号为正弦信号，幅值为2.5 mA(额定值的25%)，驱动频率分别为1，5，10，50，100，200，250 Hz，分别可获得对应频率下输出流量的幅值，由流量的幅值和频率的关系，可得所仿真伺服阀的幅频特性曲线如图10所示。由图10可得所仿真伺服阀的幅频宽约为235 Hz。

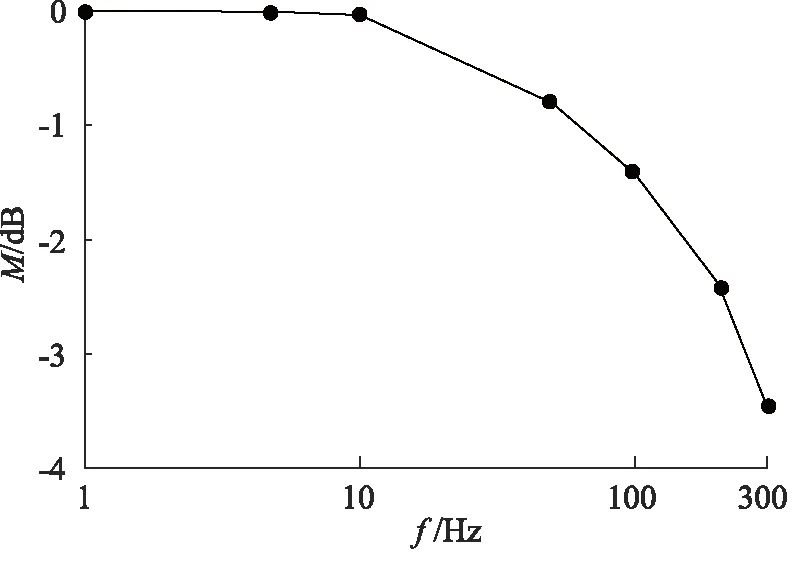
图10 幅频特性曲线

供油压力为21 MPa，MOOG 31伺服阀的频率特性曲线如图11所示[11]。由图11可知，25%额定信号输入下(2.5 mA)，其幅频宽约为250 Hz，稍大于物理模型仿真结果。

4 结论

为解决伺服阀准确的数学模型复杂，不易求解和工程应用的问题，本研究采用物理建模的方法对双喷嘴挡板力反馈两级电液伺服阀进行了建模仿真。由建模过程可知， 基于物理建模的方法仅需对伺服阀工作

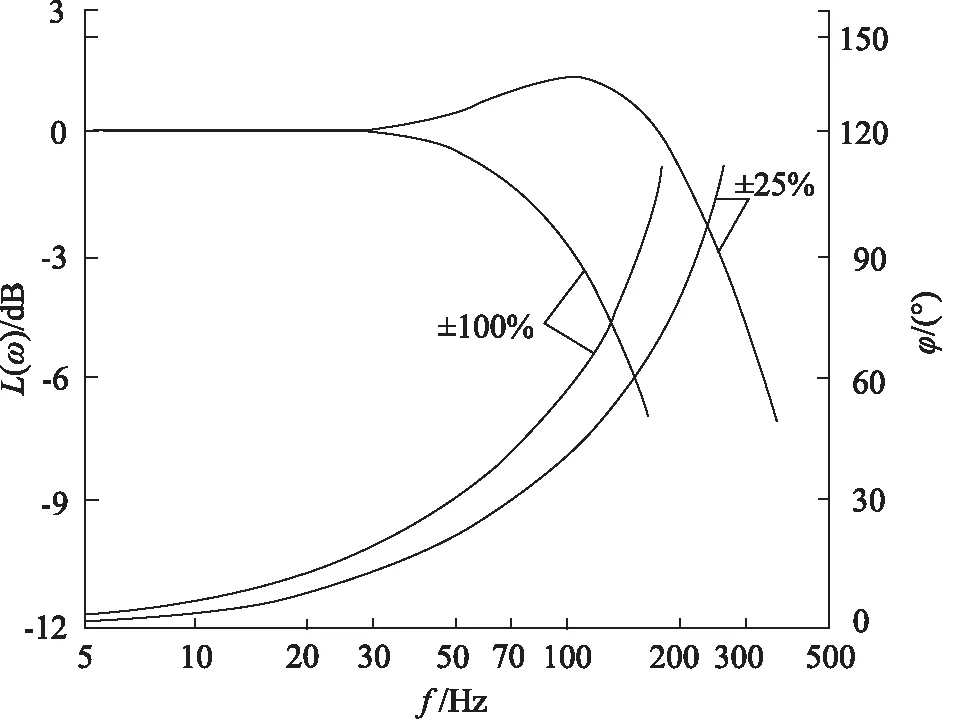
图11 MOOG 31伺服阀频率特性

的机理深入了解即可建立比较准确的物理模型。仿真过程中不涉及复杂的传递函数和限制条件下的简化。所得结果与数学模型所给结果接近。另外物理模型可以方便的考虑磁滞非线性的影响，可以忽略这种影响，本模型中不计磁滞影响。