基于介质层耦合的柔性触觉传感器空间分辨率补偿方法研究
2021-04-23陈英龙解佳森朱沣樟王斌丞弓永军
陈英龙, 解佳森, 朱沣樟, 王斌丞, 弓永军
(大连海事大学 船舶与海洋工程学院, 辽宁 大连 116000)
引言
近年来,随着经济的发展、科技的进步以及人们生活水平的提高,人机交互机器人正逐步融入医疗检测、教育等领域[1-2]。触觉作为感知信息的一种关键方式,在人机交互过程中起着非常重要的作用。因此,一种全柔性并且可大面积穿戴的电子皮肤成为了科研人员研究的热点之一[3-4]。MITTENDORFER等[5]设计的一种模块化的触觉传感单元,可构成不同大小的敏感“皮肤”实现触觉感知。上述触觉传感器用作仿生皮肤时多采用刚性基体,缺乏应有的柔性和可穿戴性,在人机交互智能机器人弯曲部位中不宜广泛应用。SHIRAFUJI S等[6]使用聚偏氟乙烯柔性压电薄膜制作了一种仿生皮肤,可用于测量滑觉信息,但缺乏对静态力的感知。CHOONG C L等[7]介绍了一种高灵敏度、高拉伸性的压阻式触觉传感器,电阻能量损耗较大。由于柔性电容式压力传感器具有体积小、灵敏度高、低噪声、耗能少、温度漂移少等特点而受到广泛的关注[8],并应用于多种电子设备中,例如电子皮肤、可穿戴电子设备等。黄英等[9]提出一种全柔性电容式触觉传感器,并设计成两种不同的分离式阵列单元。WEI Peiqi等[10]介绍了一种多孔状复合介质层电容式柔性离散型触觉传感器,空间分辨率较低,且阵列传感器的尺寸较小,具有操作复杂、成本高等缺点。王迪等[11]研究单向大面积压缩模式下聚二甲基硅氧烷(简称PDMS)软材料的膨胀变形模型。窦海斌等[12]针对液压作动系统的传感器故障检测开展研究工作,通过1个线性转换将液压系统的初始模型转换成2个子模型,1个模型只含系统的不确定性,而另1个子系统只含传感器故障,从而实现了不确定性和传感器故障的完全解耦。冯世泽等[13]针对某特种液压缸内置磁致伸缩位移传感器发讯异常问题,使用 ANSYS Electronics 对磁环通过油管后的径向磁感应强度分布进行了仿真分析,同时结合试验研究得出磁环磁感应强度经不同相对磁导率油管作用下的磁感应强度,仿真与试验结果基本一致。通过优化油管加工工艺,消除了油管的铁磁性,解决了位移传感器发讯异常问题。
以具挑战性且应用潜力较大的接触压力测量的TAKEI K等[14]和汪浩鹏[15]的电子皮肤触觉传感器为例,其空间分辨率分别为4.0 mm×4.0 mm和4.5 mm×6.0 mm,接近人类皮肤。CHANDRA M等[16]提出了一种有2个电容的传感单元的解决方案,电容排列紧凑,虽然使电容式触觉传感器的空间分辨率提高1倍,但分辨率仍然较低。CHANDRA M等[17]通过共用电极的2个电容的垂直叠加,在x和y方向上的空间分辨率增加了1倍,还通过理论设计等对法向力和剪切力进行了传感演示,但仍存在空间分辨率偏低等问题。WATATANI K等[18]提出了一种新型的“阵列式”单片电路类似指纹的触觉传感器,可以获取触觉信息的高分辨率图像表面,虽然获得了100 μm的空间分辨率,但制作工艺复杂、成本较高。
针对现有的柔性电容式压力传感器存在空间分辨率偏低等问题,提出了一种基于整体介质层耦合结构的柔性传感器,并且将建立传感器接触及扩散电容单元的数学模型,通过接触及扩散电容对接触位置进行准确判断,显著提高电容式柔性压力传感器的空间分辨率,可以应用于智能机器人对微小尖锐物体的精准抓取。
2 耦合式柔性触觉传感器设计
2.1 阵列触觉传感器模型与工作原理
电容式柔性触觉传感器模型三维结构三视图如图1所示,其结构可与平行板电容等效。因PDMS具有柔性、透明性、良好的延展性和生物兼容性等优点,本研究选用PDMS作为电容式传感器的上、下层衬底,将一定量的PDMS主剂和固化剂以10∶1的体积进行配比,滴在KW-4B型匀胶机玻璃片上,通过控制匀胶机的转速和匀胶时间可得到指定厚度的衬底。近年来,研究人员提出利用“渗流理论”混合导电性能较好的纳米颗粒来提高介质层的介电性能,以改善传感器的静态特性。因碳系导电填料种类丰富,具有不易被氧化,同时能够保证高分子材料的物理性能和机械性能,且稳定性优于金属纳米颗粒、成本较低等优点,而被广泛用于填充介质层填料。选用质量分数为2.5%[19]的乙炔黑或者碳纳米管[20]填充PDMS混合试剂介质层纳米颗粒,将抽真空后的介质层复合物倒入3D打印的模具中,再放入真空烘干箱中,烘干待用。选择一定长径比的碳纳米管, 制作柔性电极板。最后传感器封装方式选用PDMS自封装[21]。
在传统电容式柔性触觉传感器表面施加力F时(假设受力时极板面积不发生变化),由于考虑力F作用面积较大,作用区域内弹性介质层厚度会均匀减小Δd,缺少在力F作用耦合介质层下的相关模型研究。建立的模型,是当力F作用面积相对较小时,受力区域内的介质层厚度变化不均匀,受力区域下凹介质层呈圆锥形,在此基础上建立耦合式介质层受力后的数学模型,并进行分析。
2.2 阵列触觉传感器耦合介质层的模型分析
传感器施加的外力F与传感器下凹圆锥型有一定的函数关系,即F=f(r0,h),其中r0表示圆锥的底面半径,h表示圆锥的高。受力F作用后介质层下凹的圆锥面方程为:
(1)
其中,Z表示圆锥侧面上一点距离锥顶所在平面的距离;x0,y0分别表示受力接触点的横、纵坐标;x,y分别表示横、纵坐标轴的变量参数。
1) 单个传感器介质层变形模型
当在阵列传感器衬底上施加一个较小的作用力F1,该作用力只引起某一个传感器的电容变化,在该传感器内形成下凹的小圆锥,如图2所示。
如图3a所示的圆锥分析图,底面半径为r,圆心为m,高为h,母线为L。
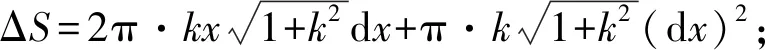
(2)

图3 圆锥几何分析图
其中,C0表示初始电容;εr表示纳米颗粒填充到PDMS硅橡胶的初始相对介电常数,其值与纳米颗粒在基体中的填充量V、施加力F、弹性电介质厚度d0的变化量Δd有关,下同;ε0表示真空介电常数;d0表示传感器两极板间的初始距离;A表示电极板面积。
(3)
其中,dc表示小圆台侧面积引起的电容值;θ表示圆台侧面与其平行于下极板投影面的夹角。
N个小圆台传感器并联在一起,已知并联电容器电容求和与积分公式,联立式(2)、式(3)得:
(4)
其中,C表示单个传感器受力后的电容值;h表示圆锥的高。
2) 阵列传感器介质层耦合变形接触模型
当施加一个较大的作用力F2时,作用区域包含多个传感器,即多个传感器的电容会发生变化,在多个传感器内形成下凹的大圆锥情况如图4所示。

图4 传感器受力示意图
对受力传感器建立高分辨率数学模型。该模型中忽略各个传感器电极板之间的间隙。以阵列中传感器a的中心为原点建立Oxyz三维坐标系,如图5所示。
结合式(1),已知大圆锥的半径为r0,高为h,如图5所示,由几何关系得:

(5)
其中,d表示传感器受力后两极板间的距离。

图5 阵列传感器三维坐标系简图
小传感器半径为q0,传感器b的中心点坐标为(2q0,0),传感器c的中心点坐标为(0,2q0),设接触点在xOy平面内的坐标为(x0,y0),则在力F作用下介质层下凹的圆锥锥顶在xOy平面内的坐标也为(x0,y0),如图6所示。

图6 阵列传感器二维坐标系简图
所有受力区域的传感器根据电容公式(2)和二重积分原理都可以分别列出一个含有x0,y0,h等未知数的方程式,构成方程组,联立起来即可解出未知参数x0,y0,h的值。相对介电常数εr与d0的变化量Δd成正相关[9],设εr=f(V,d0-h)。直角坐标系和极坐标系的参数转化关系:x=rcosθ,y=rsinθ,dxdy=rdrdθ,由此可得:
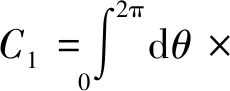
(6)
其中,C1表示传感器a的电容值。
结合图6的坐标系,由上述传感器a的电容计算公式(6)经过坐标平移可得传感器b、传感器c的电容计算公式分别为:
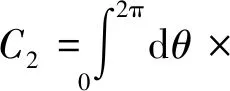
(7)

(8)
其中,C2,C3分别表示传感器b,c介质层厚度变化后的电容值。
3 耦合式柔性阵列传感器模型仿真分析
为了验证上述耦合式介质层阵列传感器空间分辨率的补偿方法模型公式的合理性及正确性,使用MATLAB对其进行程序仿真试验分析。
3.1 耦合介质层单个传感器模型仿真分析
用仿真软件对介质层变形小圆锥模型即式(4)进行试验仿真,取6≤εr≤8进行模型仿真[19],下同。测得该传感器的电容值C与介质层变形圆锥的高h之间的曲线关系如图7所示,分析曲线可知:圆锥的高h与电容值C的曲线斜率逐渐增大,保持其他参数不变,在一定范围增大圆锥的高h时,电容值C也随之增大,可以得出传感器的电容值C与圆锥的高h呈正相关。
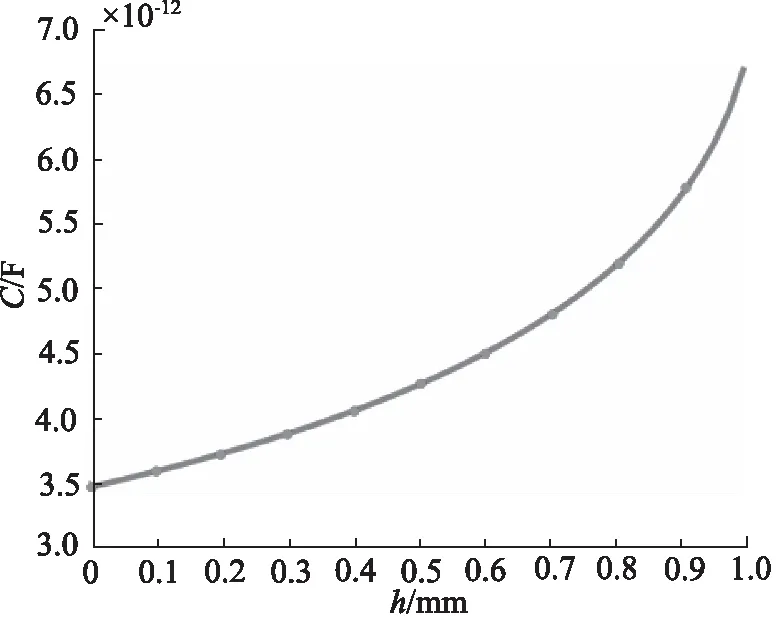
图7 小圆锥模型仿真曲线
3.2 耦合介质层阵列传感器模型仿真分析
在阵列传感器上施加一个力F,在受力区域内一定能出现3个相邻且电容值变化最大的传感器,即传感器a,b,c,且电容值分别为C1,C2,C3,选定传感器a的电容值最大,即接触点在传感器a上,且C1>C2=C3。接触点(x0,y0)一定在以O为圆心、以a0为半径的圆上,则x0=a0cosα,y0=a0sinα,其中α表示a0所在直线与x轴所夹的锐角,α的取值范围是0≤α≤π/2,方程如式(9)所示,b0,c0所列方程同理。
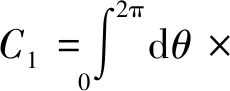
rdr
(9)


图8 触觉锥原理示意图
取q0=5 mm,设定h/r0=0.05。对式(6)~式(8)阵列传感器接触模型进行程序仿真试验。选取α=0,则x0=a0,y0=0,代入模型公式,编写程序进行仿真,得到电容值C与h,a0,b0,c0之间的曲面图,如图9所示。分析图中曲线的变化趋势可知,保持其他参数不变:
(1) 当a0,b0,c0一定时,电容C随h的增大而增大,如图9b的曲线L1所示。曲线L1表示当a0=b0=c0=0.005 m时,C随h的增大而增大的曲线;
(2) 当0≤a0≤0.005 m,0≤b0≤0.015 m,0≤c0≤0.015 m 时,C1随a0的增大而减小,C2随b0的增大而减小,C3随c0的增大而减小,如图9c的曲线L2所示。曲线L2表示当h一定时,C随a0/b0/c0的增大而减小。在0≤a0≤0.005 m顶部区域出现波峰波谷,如图9中浅色区域所示,可能的原因:因电容值过大而超出了该传感器的量程,造成了该部分曲线出现不规则的起伏。

图9 触觉锥模型仿真曲线图
已知0≤h 针对目前电容式柔性触觉传感器的空间分辨率偏低等问题,设计了耦合式介质层结构的阵列传感器,基于阵列传感器力接触模型电容式(6)~式(8),通过算法补偿对耦合阵列传感器力接触点位置进行精准求解,该模型大大提高了智能机器人与较尖锐物体接触的空间分辨率。编写该模型的MATLAB仿真试验验证程序,对前面仿真求解试验结果进行仿真试验验证。验证结果显示,保持其他参数不变, 输入一组C1,C2, 图10 仿真求解数据曲线图 C3的值依次增大时,输出对应的h随之增大,如图11中a)所示,验证了电容C与高h之间的关系呈正相关;输出对应的的x0和y0(且x0=y0)随之减小,如图11中b)所示,验证了电容C与接触点(x0,y0)的坐标值之间的关系呈负相关; 同时也验证了模型式(6)~ 图11 仿真试验验证曲线图 相关文件程序伪代码如下: Alogrithm 1: Coupled Array Sensor Model CompensationInput: C′1, C′2, C′3syms h′, x′0, y′0, r, θε0←8.854, εr←6, d0←0.001, q0←0.005, h/r0←0.05Set up a 3 by 4 matrix for h′,x′0,y′0, C′1 C′2, C′3h′←h; x′0←x0; y′0←y0h′, x′0, y′0← solveC′1=∫2π0dθ∫q00ε0·εrd0-h′+hr0(rcosθ-x′0)2+(rsinθ-y′0)2·rdrC′2=∫2π0dθ∫q00ε0·εrd0-h′+hr0(2q0+rcosθ-x′0)2+(rsinθ-y′0)2·rdrC′3=∫2π0dθ∫q00ε0·εrd0-h′+hr0(rcosθ-x′0)2+(2q0+rsinθ-y′0)2·rdrìîíïïïïïïïïïïïüþýïïïïïïïïïïïreturn h′, x′0, y′0 提出了一种基于耦合式介质层结构柔性阵列传感器,其应用于电子皮肤的柔性电容式传感器的制作尺寸较大、操作简便、成本较低,可大面积应用于人机交互机器人的弯曲部位,具有较强的可扩展性及可移植性,避免了刚性传感器不宜穿戴、维护性差等缺点,可实现真正意义上精确的触觉感知功能。 建立了传感器接触及扩散电容单元的数学模型,在不降低电极面积的前提下,能够对接触位置进行准确判断,显著提升了柔性电容式阵列传感器的空间分辨率,其为0.2 mm×0.2 mm。阐述了该柔性电容式触觉传感器的制作材料、工作原理、柔性传感器结构模型、分辨率数学模型以及介质层一体化结构设计等,同时使用MATLAB仿真软件进行数学模型试验仿真,仿真结果验证了柔性电容式阵列传感器耦合式介质层的算法模型正确性及精确性,同时也显著提高了阵列传感器的空间分辨率。4 耦合式阵列传感器模型补偿算法


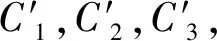

5 结论
