基于XGBoost算法的草甸地上生物量的高光谱遥感反演

张亦然，刘廷玺，2*，童新，2，段利民，2，吴宇辰

（1.内蒙古农业大学水利与土木建筑工程学院，内蒙古呼和浩特010018；2.内蒙古自治区水资源保护与利用重点实验室，内蒙古 呼和浩特010018）

草甸地上生物量能很好地反映草地生长状况，是牧草产量预测的重要指标，高时效、高精度模拟估算草甸地上生物量，可为合理利用草地资源、平衡牧区草畜供求关系、促进天然草地畜牧业发展提供定量的科学依据［1-3］。相较费时费力且存在破坏性的传统地上生物量测量法，遥感技术则被认为是实效、客观、准确地模拟估算草甸地上生物量的一个重要工具［4］。基于遥感技术快速模拟估算草甸地上生物量，并建立技术方法和理论，可进一步促进草地生态系统健康评价和草地资源可持续利用与管理。

多光谱遥感数据在研究草甸地上生物量存在的主要局限性在于其范化的光谱分辨率，这使得植被冠层的详细反射特征被掩盖［5］，且针对一定区域的精准计算，效果较差。而高光谱遥感具有连续波段数量多、光谱分辨率高等特点，可在冠层尺度上提供有关植被生物理化更详细的信息，能可靠地量化草甸地上生物量［6］。且近年来，随着高光谱遥感技术的发展，在土壤养分盐分监测［7］、作物生理生长参数反演［8］、放牧场利用强度评估［9］等研究中也得到较大的应用。故对于一定区域的冠层尺度上精细刻画牧草生物量，运用高光谱遥感技术是极其必要的。

基于高光谱遥感技术观测的草甸地上生物量已日益成熟。在方法上大多运用多元统计方法构建模拟估算模型［10］，并为了进一步提高预测能力及模型的精度，可对植被指数进行优化［11］、结合光谱变换［12］等形式改进，或利用诸如偏最小二乘法、随机森林等机器学习算法对草甸地上生物量进行反演估算［13］，其效果显著。近年来，作为一种新兴的深度机器学习优化算法，极限梯度提升（extreme gradient boosting，XGBoost）算法［14］能适应复杂的非线性关系，模型具有更佳的并行处理能力，对于如牧草收获的一定范围区域、实地获取的野外小样本数据量，可以有效解决在机器学习回归模型中可能出现的过拟合问题，因此，可作为构建一定区域内草甸地上生物量模拟估算模型的有效方法，且多方法协同应用于草甸牧草生物量的研究还较少，这对于高光谱遥感技术在农牧业中的发展具有促进作用。

综上考虑，本研究在冠层尺度上，对收获期前的牧草进行高光谱测定与生物量获取，采用XGBoost算法与光谱变换、优化植被指数法协同建立草甸地上生物量模拟估算模型。验证XGBoost算法在草甸地上生物量模型构建中的可适用性，扩展高光谱遥感技术对区域性的牧草量化。以期为天然牧草的生物量评估提供科学参考，同时提升高光谱遥感在精准农牧业发展中的应用价值。

1 材料与方法

1.1 研究区概况

研究区位于科尔沁沙地东南边缘，地理坐标为122°33′00″-122°41′00″E，43°18′48″-43°21′24″N，面积为55 km2，区内地势走向为西高东低，南北高，中间低，海拔为184～235 m，地貌类型丰富，主要为沙丘-草甸相间地区，中部为小型湖泊（图1）。该区属半干旱大陆性季风气候，多年平均空气温度6.6℃，多年平均降水量389 mm，多年平均蒸发量（Ф20 cm口径蒸发皿）1412 mm。区内农牧民以畜牧业和种植业为主要生产方式，研究区南北部沙丘上的灌木草场和湖泊周围的草甸为牲畜的重要牧草来源。

图1 研究区所在位置和试验点布设Fig.1 Location of the study area and the test sites

采样点位于区内湖泊北侧草甸草场上的C3和C4站点（图1），主要植被类型为芦苇（Phragmites australis）、羊草（Leymus chinensis）、鹅绒委陵菜（Potentilla anserina）和蒲公英（Taraxacum mongolicum）等。鉴于C3站点以南为草甸，以北为农田，故以C3站点为起点，向南每隔10 m设定一个采样点，自南100 m处分别向东、西每隔10 m设定一个采样点，共布设30个采样点；鉴于C4站点周围均为草甸，故以C4站点为中心，分别沿东、西、南、北4个方向，每隔20 m设定一个采样点，与站内一个采样点，累计布设30个采样点。每个采样点均用高精度GPS进行记录。

1.2 数据采集与处理

1.2.1 高光谱遥感数据采集与处理 使用美国ASD（Analytical Spectral Devices，Inc）便携式光谱仪Field Spec 4采集天然草甸冠层高光谱反射率数据，仪器波段范围350～2500 nm，光谱采样间隔在波段350～1000 nm时1.4 nm，在波段1001～2500 nm时2.0 nm，光谱分辨率分别为3和8 nm。于2019年7月31日对C3、C4两个试验点布设的60个采样点进行高光谱反射率数据的采集，当天晴朗、无云、微风，C4、C3试验点采集时间分别为10：40-11：50、12：10-13：40。仪器视场角为25°，传感器探头垂直向下，距冠层顶高度70～80 cm，设置平均采集数为10，对每个采样点进行2次重复测量，即每一个采样点获取20个数据，测量时每隔15 min进行1次白板优化。

利用ASD高光谱数据处理软件ViewSpec Pro对原始光谱数据进行处理，由于每个采样点有20条光谱曲线，首先需进行光谱异常筛选，剔除差异较大、错误的光谱曲线，然后对余下各光谱波段取均值得到最终光谱曲线，最后进行平滑去噪、一阶与二阶光谱微分变化处理。由于草甸地上生物量在可见光至近红外波段内与光谱反射率关系密切［15-16］，且此光谱波段范围的信噪比低，故本研究选取400～900 nm波段范围的光谱数据进行研究。

1.2.2 地上生物量数据采集与处理 针对两站点布设的60个采样点，运用地物光谱仪测定牧草冠层光谱反射率，根据仪器视场角的投影范围确定齐地刈割牧草的样方大小，范围为0.3～0.5 m2，现场称其鲜重，并带回实验室，在105℃杀青30 min，65℃烘干至恒重后称重，计算地上生物量（aboveground biomass，AGB，g·m-2）［17］。

1.3 数据分析方法

运用Sklearn库中的互信息回归（feature_selection.mutual_info_regression）法分析光谱反射率和光谱指数与生物量之间的线性、非线性关系。互信息度取值范围为［0，1］，等于0时，表示两个变量之间相互独立，等于1时则表示两个变量完全相关［18］。

先将不同阶数高光谱反射率与草甸地上生物量进行相关性分析，寻找与地上生物量有相关性的波段。然后将各阶全波段光谱反射率代入到常用的7个植被指数公式中（表1），挑选出最优波段组合用以构成不同阶全波段高光谱植被指数，最后将不同阶植被指数组合构成3个输入变量数据集，利用多元统计与机器学习方法对地上生物量进行模拟，建立高光谱植被指数与草甸地上生物量反演估算模型。

表1 植被指数及相关计算公式Table 1 Vegetation indexes and related formula

1.4 模型构建方法

在python 3.7的编程环境下，通过Sklearn与XGBoost程序库构建了多元线性回归（multiple linear regression，MLR）、随机森林（random forest，RF）和极限梯度提升（XGBoost）3种地上生物量反演估算模型。所建各模型的输入变量共构建3个数据集，数据集1、2、3分别由基于原始（零阶微分）、一阶微分、二阶微分光谱反射率计算的7个最优高光谱植被指数组成。

1.4.1 多元线性回归模型 多元线性回归（MLR）是遥感反演最基础的方法之一。由多元线性回归方法构建的地上生物量反演模型称作MLRM模型。算法原理如下：

式中：yipred为地上生物量估算值；｛β1，…，βi｝为回归系数；｛x1，…，xi｝为输入变量集，即不同类型光谱植被指数集。

1.4.2 随机森林模型 随机森林（RF）是对大量分类数汇总的集成算法。由随机森林方法构建的地上生物量反演模型称作RFM模型。对于不平衡数据集来说，随机森林法可以平衡误差［26］。算法原理如下：树的集合为｛ht，t=1，2，…，Ntree｝，对待测样本输入变量集xi，回归树ht输出ht（xi）

1.4.3 极限梯度提升模型 极限梯度提升（XGBoost）是在传统的Boosting基础上，利用中央处理器（central processing unit，CPU）的多线程，引入正规化项，进一步控制了模型的复杂度［14］。由XGBoost算法构建的地上生物量反演模型称作XGBM模型。XGBoost的集成模型通过K（树的数目）个基模型组成一个加法运算式来预测最终结果：

式中：zt表示第t棵树的目标函数，表示前t-1棵树的输出值之和，ft（xi）表示第t棵树的输出结果，l是一个用来衡量预测值yipred和真实值yi之间差异的可微凸目标函数，γ（fk）是表示模型复杂度的惩罚项，ε是表示叶子数据的正则化参数，ϑ是表示叶子权重的正则化参数，ω是表示叶子节点的取值。将损失函数在处利用泰勒公式展开：

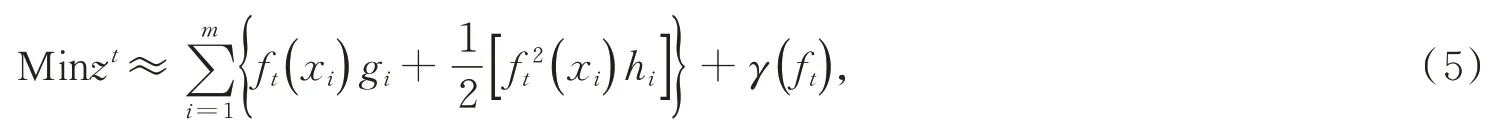
其中，

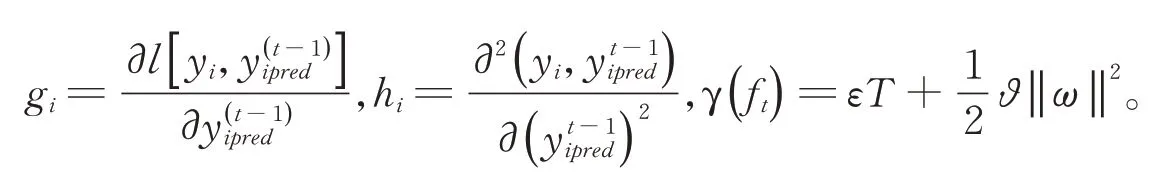
将正项代入式（5）得

对XGBoost来说，叶子权重就是所在叶子节点上的样本在这棵树上的回归值，一般用ω表示。定义Ij={i|q(xi)=j}为第j个叶子节点上的样本集合，，其中，ωj表示叶子节点j的权重。将每个叶子的一阶梯度统计量和二阶梯度统计量求和，即。则式（6）可改写为：

由式（7）可以得出叶子节点权重的计算公式为：

将式（8）带入式（7），得：

1.5 XGBM模型调参

为提升模型的模拟反演精度，在构建XGBM模型前，需对参数进行合理调整，具体的调参过程如下。

1.5.1 弱评估器的数量 XGBoost算法中的弱评估器数量（t）是影响最终模型精度的首要参数，如果弱评估器数量过多，会导致模型过拟合且运算速度下降。由学习曲线（图2）可知，数据集1弱评估器数量为0～30，平均绝对误差（mean absolute error，MAE）值急剧下降，在37处MAE为最低值，之后逐渐趋于平稳，故数据集1取最佳弱评估器的数量为37个。按照相同原则，数据集2、3下的弱评估器数量最终分别取55和42个。

1.5.2 其他参数的调节 通过学习曲线及网格搜索优化出步长（learning_rate）、树的最大深度（max_depth）、最小叶子权重（min_child_weight）、最小损失函数下降值（gamma）等每组训练集的关键参数，参数优化结果如下：当输入变量为数据集1时，步长为0.41，树的最大深度为2，最小叶子权重为2，最小损失函数下降值为0.02；为数据集2时步长为0.10，树的最大深度为2，最小叶子权重为4，最小损失函数下降值为0.03；为数据集3时步长为0.11，树的最大深度为1，最小叶子权重为1，最小损失函数下降值为0.07。

图2 学习曲线Fig.2 Learning curves

1.6 模型精度验证方法

模型精度评价采用均方根误差（root mean square error，RMSE）、平均绝对误差（MAE）、Nash效率系数（Nash-Sutcliffe efficiency coefficient，NSE）［27］和 一 致性指数（index of agreement，d）［28］4个指标来评价。计算公式分别为：

式中：yi为地上生物量的实测值；为地上生物量实测值的平均值；yipred为地上生物量的估算值；i为采样点号，m为样本数量。Nash效率系数可反映模型预测值与实测值之间的接近程度，取值为-∞～1，一致性指数是对基于相关性的精度评价系数的一种改进，取值为0～1。当RMSE、MAE值越小，NSE、d越接近1时，表示模型的精度越高。

2 结果与分析

2.1 光谱反射率和地上生物量的相关性分析

采用互信息回归法分别对试验区草甸地上生物量与原始、一阶与二阶微分冠层光谱反射率进行相关性分析，其中，互信息度用以表示相关性，互信息度越大，则相关性越强（图3）。

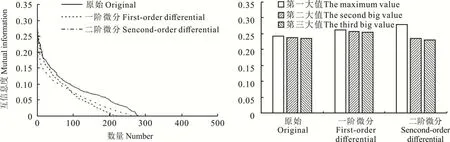
图3 草甸地上生物量与各类高光谱反射率的相关性Fig.3 Correlation analysis of the hyperspectral reflectance and AGB using the mutual information method

原始、一阶微分、二阶微分光谱反射率与草甸地上生物量具有相关的波段数分别为284、221和265个（图3），均占总波段数的近3/5，表明同原始光谱反射率一样，一、二阶微分光谱反射率都与草甸地上生物量有一定的相关性。原始、一阶微分、二阶微分光谱与地上生物量的互信息度最大值依次变大，分别为0.2382、0.2451和0.2615）（图3）。尽管二阶微分光谱反射率与草甸地上生物量相关性波动较其余两者都大，但整体来看3者的互信息度均不高，因此有必要对原始以及微分变换后的光谱反射率数据进行波段选择，构建高光谱植被指数对地上生物量的模拟估算模型。

2.2 高光谱植被指数与地上生物量的相关性

在选取的400～900 nm光谱波段范围内，将每一波段原始、一阶以及二阶微分反射率光谱值分别以归一化植被指数（NDVI）、比值植被指数（RVI）、土壤调节植被指数（SAVI）、优化土壤调节植被指数（OSAVI）、增强型植被指数2（EVI2）、重归一化植被指数（RDVI）、修改型土壤调节植被指数（MSAVI）7个植被指数的形式进行组合（表2），采用互信息回归法计算互信息度，图4～6给出了基于原始、一阶和二阶微分光谱植被指数与草甸地上生物量的相关性矩阵。综合来看，无论是原始光谱反射率还是一、二阶微分光谱反射率，基于归一化植被指数（NDVI）与比值植被指数（RVI）计算所得的相关性矩阵图形式上十分相似。而基于其余5种植被指数计算得到的相关性矩阵图形式也大体一致。基于原始光谱反射率的植被指数与草甸地上生物量相关性矩阵图中，较高的互信息度呈面状分布、区域上较完整连续，而一、二阶微分光谱反射率植被指数与地上生物量相关性矩阵图中，较高的互信息度却呈破碎的斑块状，同时破碎程度随着阶数的增加而增加。原始光谱反射率的植被指数中，NDVI、RVI、SAVI及OSAVI与草甸地上生物量的互信息度最大值达到0.4以上，其余植被指数互信息度最大值也超过0.32（图4）。一阶微分光谱反射率植被指数与地上生物量的互信息度均达到0.5以上（图5）。二阶微分光谱反射率植被指数与地上生物量的互信息度较一阶微分植被指数有所下降，但相关系数最大值也均在0.32以上（图6）。最优光谱植被指数及其对应的波段组合见表2。

表2 最优植被指数及其波段组合Table 2 Optimal vegetation indexes against AGB and the corresponding band combinations

基于原始光谱反射率构建的不同最优植被指数除EVI2（波段组合为769 nm近红外、746 nm红边）外，其余植被指数均为红边与近红外波段的组合形式（表2）。基于一阶微分光谱反射率构建的最优SAVI、OSAVI、EVI2和MSAVI波段组合完全相同，均为527 nm绿光波段、751 nm近红外波段的形式。基于二阶微分光谱反射率构建的不同最优植被指数均为绿光或者蓝光与红边波段的组合形式，其中，530 nm绿光波段与740 nm红边波段组合最多。就与草甸地上生物量的相关性互信息度而言，基于一阶微分光谱反射率计算的各最优植被指数最高，原始与二阶微分光谱反射率次之，且均高于基于单一波段的互信息度，说明构建全波段范围最优植被指数能够有效提升高光谱反射率数据与地上生物量的相关性，通过光谱微分变换处理后构建的最优植被指数在很大程度上优于原始光谱反射率构建的植被指数。

图4 基于原始高光谱反射率的植被指数与草甸地上生物量的相关性矩阵Fig.4 Correlation matrix plots of the original all available wavebands vegetation indexes and aboveground biomass（AGB）using the mutual information method

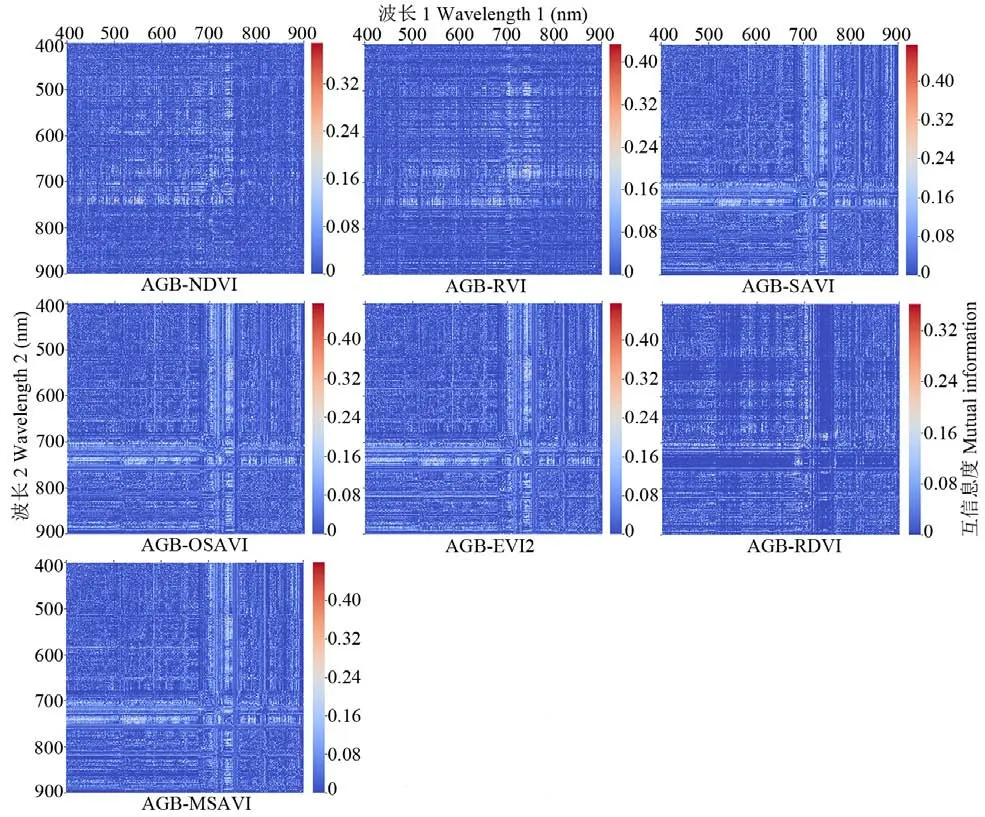
图6 基于二阶微分高光谱反射率光谱的植被指数与草甸地上生物量相关性矩阵Fig.6 Correlation matrix plots of the second-order differential all available wavebands vegetation indexes and AGB using the mutual information method

2.3 地上生物量模型对比分析

基于构建的3组输入变量数据集，采用MLR、RF以及XGBoost算法进行草甸地上生物量模拟估算模型的构建，基于每个数据集的3类模型估算及评价结果示于图7。

针对同一个算法所构建的模型而言，MLRM模型综合表现最好的输入变量为数据集3（图7），但其NSE（0.40）低于数据集2（0.67），图中表现的一致性程度较差。而RFM模型和XGBM模型下的最佳输入变量均为数据集1，其次分别为数据集2、数据集3，即输入变量为原始光谱植被指数时，两个机器学习算法所构建的模型精度最佳，同时也说明微分处理后的光谱植被指数在机器学习模型中反而会降低模型的精度。

针对同一输入变量数据集，MLR模型估算值与实测值较其他两个模型在1∶1线旁分布离散，且在数据集1下这种差异性最为明显，说明MLR模型整体的精度最低、模拟效果最差，这可能是由于光谱反射率与生物量之间并不存在纯粹的线性关系；也反映出MLR方法并不能解决输入变量的多重共线性问题。而XGBM模型与RFM模型实测值与预测值的分布在图中表现较相似，但XGBM模型的RMSE、MAE值均最小（140.26 g·m-2、97.20 g·m-2），NSE、d值均最接近于1（0.81、0.94），因此，XGBM模型模拟估算草地地上生物量较稳定，且精度较高。由此可见，当输入变量为数据集1时，基于XGBoost算法构建的草甸地上生物量模拟估算模型精度最佳。

3 讨论

地面遥感可近距离采集植被冠层的光谱信息，且可以捕捉到真实的草甸植被光谱特征［29］，通过对冠层原始光谱反射率进行一阶、二阶微分处理，对比分析发现，与已有研究相同，微分变换可突出显示光谱信息之间的差异，消除背景噪声［30］，使得与地上生物量的相关性得到很大程度地提升。但基于二阶微分变换后的光谱与地上生物量的相关性波动较大，可能受群落植被组成及其周围环境的影响所致。

图7 不同模型估算及评价Fig.7 Results of each model with related accuracy parametersRMSE、MAE、NSE、d分别代表均方根误差、平均绝对误差、Nash效率系数、一致性指数。RMSE，MAE，NSE and d respectively represent root mean square error，mean absolute error，Nash-Sutcliffe efficiency coefficient and index of consistency.

植被指数法作为高光谱遥感技术提取植被生物理化信息的一个重要工具，常选择不同光谱波段进行组合运算，使得植被信息的提取得到进一步强化［31-32］。与上述结论相同，本研究优化后的植被指数与地上生物量的相关性显著提高，且冠层光谱与生物量之间具有更高的稳定性。原因在于高光谱连续波段的不同组合可以提供必要和潜在的植被特征信息，进而量化植被的生物理化参数［33］。但在之后的机器学习模型建立中原始光谱植被指数反而表现最佳，首先归因于红边位置对叶绿素含量和结构变化的敏感性较强［34］，且有研究表明，红边区域包含的光谱信息能表征87 %的地上生物量等信息［35］，其次，可能由于机器学习算法能较好地捕捉到变量间的非线性关系及模型在调整参数上存在的一定误差所致。

机器学习算法用于遥感建模已炙手可热［36］，选择合适的算法有利于遥感估算精度的提高。在植被生物理化参数模型构建中，利用机器学习构建的模型显著优于基于传统线性回归方法所构建的模型［37］。本研究结果与其一致，说明，一方面线性回归方法不能有效明晰输入变量与生物量之间的正确关系；另一方面由于线性回归方法不能进行深度的数据挖掘学习。而机器学习算法具有更高的准确性与鲁棒性。本研究中XGBoost算法在地上生物量模型的构建中表现更出色，可进一步优化模型中变量的局限性，使模型整体更趋于稳定，对于利用卫星遥感监测草地生物量具有重要的指导意义。但在普适性方面，由于本研究样本数量较少，可能会造成研究区其他草甸草地的异值没有涵盖，且对于时间尺度来说，要考虑到不同丰水年、枯水年的生物量值，这在后续研究中需进一步验证，可为XGBM模型在草甸地上生物量反演中提供更全面的信息，实现区域尺度的多源数据协同发展，更好地为农牧业监测、生态系统管理提供技术支持。

4 结论

本研究分析了多方法协同应用的高光谱数据与草甸地上生物量的相关性，探讨了运用XGBoost算法在草甸地上生物量模拟估算中的适用能力，并与RF、MLR法构建的草甸地上生物量模拟估算模型进行对比分析。得出以下结论：

1）对植被冠层原始光谱反射率进行一阶、二阶微分及光谱植被指数变化可以提高冠层光谱与地上生物量的相关性。2）在MLRM模型中，最佳输入变量为基于二阶微分反射率的光谱植被指数；在RFM模型与XGBM模型中，最佳输入变量为基于原始反射率的光谱植被指数。3）整体而言，基于XGBoost算法构建的模型精度最高（RMSE为140.26 g·m-2，MAE为97.20 g·m-2，NSE为0.81，d为0.94），在估算草甸地上生物量方面表现出良好的准确性，且优化了模型的复杂度，提高了效率，为区域性草甸地生物量反演提供了新的方法。