基于统一硬化参量的海洋K0固结土动力本构模型
2021-04-23吴有平伏亮明黎永索
吴有平, 伏亮明, 胡 达, 张 靖, 黎永索
(1.中国电建集团中南勘测设计研究院有限公司,湖南 长沙,410014;2.武汉大学 土木建筑工程学院,湖北 武汉 430072;3.湖南城市学院 土木工程学院,湖南 益阳 413000)
1 研究背景
循环荷载下土体本构模型主要可分为4类:(1)经验模型,为计算与使用方便,此类模型是根据室内试验或现场试验的结果对其进行分析与拟合而成。如Yasuhara等[1]建立的半对数软化公式、Chai等[2]考虑初始静偏应力模型。(2)修正静力模型,主要是以单调加载条件下建立的模型为基础,引入与动力特性相关的因子进行修正,获得与动力条件下相似的结果。如Carter等[3]允许屈服面卸载时收缩(引入收缩参数),Hosseinali等[4]通过试验获得循环荷载与单调荷载下模型之间的换算关系。(3)多面模型,模型由初始屈服面、边界面及加载面(套叠面)构成,而加载面上的塑性模量随应力点的移动而变化。如Saberi等[5]考虑砂土的松散程度、Xiong等[6]考虑饱和度等因素建立的模型。(4)基于能量守恒、热力学等理论获得的本构模型,如Collins等[7]、Tourchi等[8]、Zhang[9]基于热动力学构建的本构模型。在这些模型中,多面模型因概念清晰而广泛应用。
为获得同时适用于黏土与砂土的土体本构模型,不少学者对此进行研究,并取得一定进展。Lade等[10-11]通过修改砂土弹塑性模型的屈服面函数,建立了适用于黏性土和砂性土的统一单屈服面模型。此后,Crouch等[12]建立了适用于黏土、粉土和砂土的统一三维边界面塑性模型。这些研究成果标志着土体本构模型研究进入统一模型的新时代。Yao等[13]在广义非线性强度理论的基础上,结合Lade与SMP 强度准则提出了适用于黏性土与砂性土的统一硬化模型。Halabian等[14]建立了适用于黏土与砂土的统一黏弹性模型。近年来,统一模型的适用土体得以进一步拓展,如应用于饱和结构性黏土、非饱和土、改良土等本构模型[15-17]。
总体来说,采用上述模型的计算值与实测值较为吻合,但模型所需土工参数较多,多参数耦合下的偏差反而会降低计算精度。因而参数少、精度高、实用性强的岩土本构模型已成为广大基础工程设计人员的迫切需求。随着海上风电的迅猛发展以及桩径的增大,海上风电大直径单桩基础被广泛使用,适用于风电基础桩土相互作用的简单本构模型更为设计者所期待。为此,在前人研究成果的基础上,首先选用耗散功作为硬化参量,并引入系数α对耗散功计算进行简化,推导适用于黏土与砂土的统一硬化模型;其次,在统一硬化模型基础上,进一步分析循环荷载下的加卸载路径,研究循环破坏次数的确定方法,推导孔隙水压力和硬化参数的计算方程;最后,总结循环荷载下海洋K0固结土体统一硬化模型的计算流程,并进行了例证。
2 单调荷载下统一硬化模型的建立
(1)
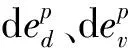
耗散应力空间原点为椭圆中心,因而真实应力与耗散应力二者相差一个迁移力,即ρ′=p′T-π′,ρ′为迁移应力,kPa;π′为耗散应力,kPa,如图1所示。图1中CSL为临界状态线。在修正剑桥模型中,该迁移应力大小为p′c/2。
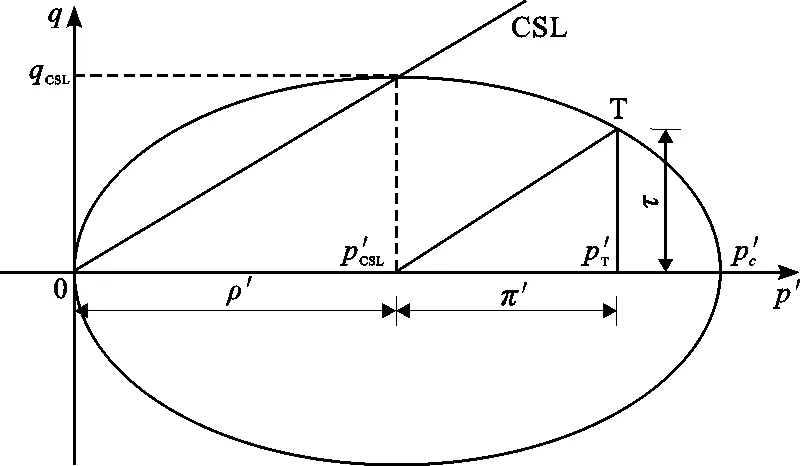
图1 p′-q应力空间中真实应力与耗散应力的关系[19]
参考文献[19]提出的耗散函数形式,对于K0固结土体的耗散功可表示为:
(2)
式中:δΦ为耗散功增量,kJ;θn为正常固结线(NCL)的倾角;A、B分别为等向压缩与剪切时描述耗散的无量纲函数;tanθn=ηK0,ηK0=3(1-K0)/(2K0+1),ηK0为NCL的斜率;K0为静止土压力系数,如图2所示。图2中,DFL为破坏状态线,NCL为正常固结线;ρ′,ζ分别为迁移应力在p′、q方向上的分量。
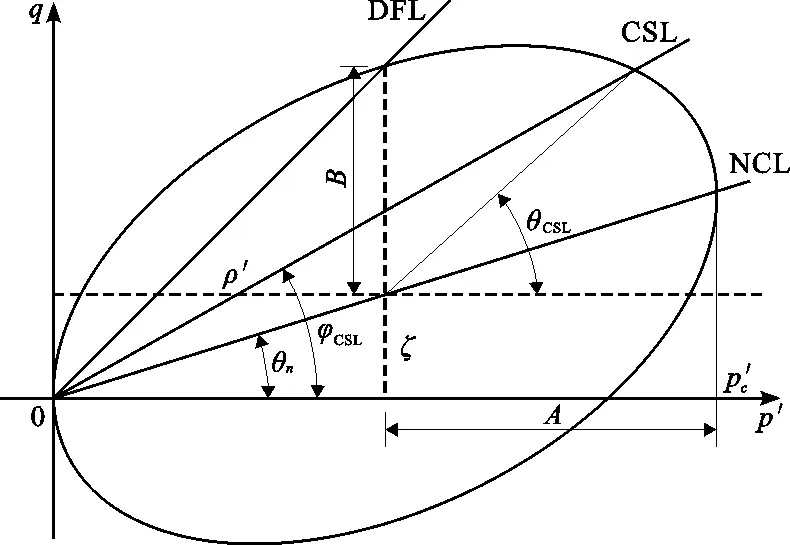
图2 K0固结土真实应力空间屈服轨迹
由图2可得屈服面函数表达式为:
(3)
假设屈服轨迹与正常固结线相交于(p′CSL,qCSL),因此p′CSL、qCSL满足公式(3)。又M=tanφCSL,A=p′c/2,可得:
(4)
(5)
代入公式(3),可获得屈服面函数为:
(6)
试验数据表明,无论是采用等向塑性体变硬化的修正剑桥模型,还是采用不等向塑性体变的硬化关口-太田模型,由模型计算获得的体应变值与试验值都存在一定的差异;为此,孙德安等[20]在考虑初始应力各向异性的基础上,提出了介于二者之间的修正。借鉴该思路对屈服面的椭圆长轴倾角引入系数β进行修正,此时倾角值为tanθβ=βtanθn。为延续前述公式,后续公式中不区分tanθn与tanθβ,计算时直接采用tanθβ替代tanθn。
本研究采用耗散功Wp作为硬化参量,结合公式(2)和(6),耗散功可表示为:
(7)

对于K0固结土体的屈服面函数可表示为:
(8)
式中:f为屈服面函数,f(σij,H)=0;p′0为初始有效压力,kPa;p′0F(Wp)为p′c的函数。
对公式(8)两边微分,可得:
(9)
式中:F′为F(Wp)函数对Wp的导数。
加工硬化规律可以采用下式来描述:
(10)
式中:dΛ为塑性变增量系数;σij为应力张量;h为硬化参数的函数;H为硬化参量,采用公式(11)计算。即:
(11)

经推导,可得:
(12)
式中:g为塑性势函数。
通过三轴试验获得应力和应变值,通过计算绘制出f-Wp关系图。采用不同围压σ3进行试验,可以获得一组曲线,然后将曲线规格化,可得f=F(Wp)函数,参见文献[21]。本文经过分析计算选用a(Wp)b的形式来表示F(Wp),其中a、b为曲线拟合获得的系数。
3 循环荷载下统一硬化模型的建立
海底土体自然形成过程中主要为K0固结,循环荷载作用时需要考虑土体屈服面的改变。采用旋转硬化和等向硬化相结合的硬化理论来表征K0固结土在循环荷载作用下的硬化规律,同时引入屈服面收缩参数Θ来描述循环荷载加载过程中土体屈服面的演化特性。等向硬化主要为在循环荷载作用下,土体屈服面往内移动缩小、累积应变值增加,当应变值达到某一值时土体破坏,即抵达内屈服面。屈服面内缩的幅度与动应力幅值、循环次数及土体性质有关。基于旋转屈服面向等向屈服面靠拢的特性,假设在循环荷载作用下旋转屈服面椭圆长轴逐渐向等向屈服面椭圆长轴靠拢,即屈服面随加载次数的增加,其椭圆倾斜长轴逐渐向水平方向旋转,在屈服面抵达内屈服面时,此时椭圆长轴处于水平位置。屈服面的中心及椭圆长轴随加载次数而变化。
设屈服面的上点坐标为(p′,q),与p′轴的交点为(p′c,p′ctanθn),则有:
(13)
对公式(13)微分,可得:
(14)

由压缩和回弹曲线e-lnp′可推算出:
(15)
(16)
(17)
式中:C为积分常数。
3.1 屈服应力的确定
假设第1次加载过程中,屈服面未变化,孔隙水压力增大,有效应力减小。后续加载过程中,土体初始为弹性加载,加载至某一屈服面时,继续加载则进入屈服阶段。如图3循环加载应力路径所示,第1次加载,由初始点A′沿A′A移动到A点,屈服面未变,然后卸载,沿AA″至A″点为弹性阶段;再次加载时,由A″点加载至B′点为弹性阶段,然后沿B′B移动到B点为塑性阶段。
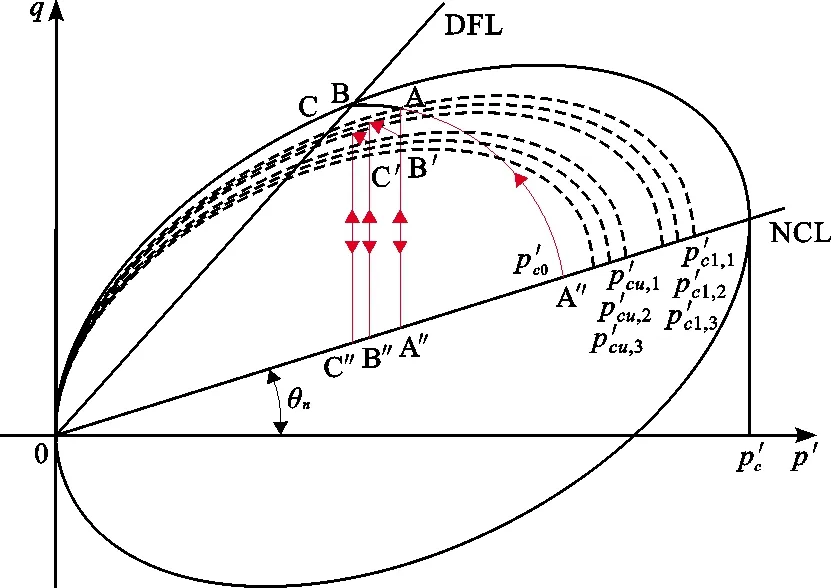
图3 循环加载应力路径
图3中的屈服轨迹可以用公式(6)函数式表示,由公式(6)可得第1次加载后的屈服应力p′c1,1表达式为:
(18)
式中:p′c1,1为第1次加载后的屈服应力,kPa;p′A、qA分别为A点处有效平均主应力与广义剪应力,kPa。
由于第1次加载过程中假设屈服面未变,因而可以认为土体的不排水剪切强度未变,不排水剪切强度cu可以采用公式(19)[3]表示:
(19)
因土体A点处和A′点处在同一屈服面上,由公式(17)可得A点处的有效应力式为:
(20)
在随后的卸载阶段,应力路径从A点到A″点,有效应力不变化。p′y,1表示对应点A″点加载参数,则卸载后对应的屈服面用p′cu,1表示为:
(21)
式中:p′y1为第1次卸载时对应的有效主应力值;p′cu,1为第1次卸载后再加载时对应的屈服面;Θ表示循环荷载下屈服面收缩参数,可以用公式(22)计算,一般为了简化计算取ξ1=0。
(22)
第2次循环加载时,应力路径从A″点到B点,屈服应力qyB为:
(23)
式中:p′yB=p′y,1。
从B′点到B点的塑性阶段,加载的计算参考公式(18)、(20)、(21)。
3.2 循环破坏次数Nf的确定
一般而言,循环破坏次数与屈服面收缩参数Θ与循环荷载水平qc有关,参数Θ与循环次数N及土体特性等有关,可以通过试验获得。具体过程为,在一定的围压下,选定不同的循环荷载水平(至少为3个),加载至循环破坏(如应变大于3%),记下此时的循环破坏次数,将其绘制于qc/(2cu0)与Nf关系图中,如图4所示。然后假设Θ为某一数值,代入公式(21)、(23)等,获得应变值,与实际测试结果进行对比分析,再根据结果调整Θ值重复前述计算,直至与实测值吻合。在Θ与qc确定后,Nf可查图获得。
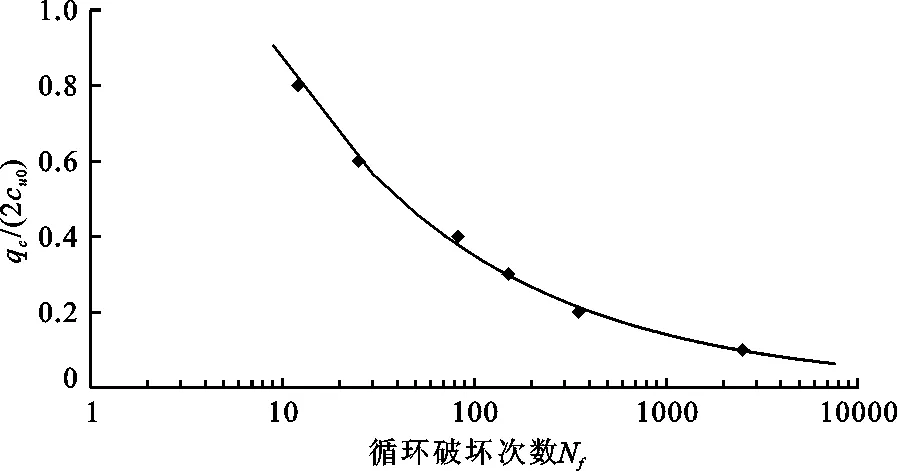
图4 循环破坏次数与循环荷载关系
3.3 旋转硬化参数
土体在K0固结时,存在结构性,故有初始角θ0,随着循环荷载的作用,土体结构性逐渐被破坏,直至在达到Nf时,结构完全破坏,土体为各向同性体。假设旋转硬化在初始时是θ0,在经过Nf次循环荷载作用后,θNf=0,每次旋转的角度(Δθ)相同,即Δθ=θ0/Nf。第n次循环的角度可以按公式(24)计算。
(24)
将式(24)代入上节公式中:重新进行参数Θ计算,作为最后的Θ值,建议在实际试验时考虑频率F的影响。
3.4 孔隙水压力计算
波浪及洋流等荷载使土体受压变形,此时孔隙水受土体结构及上部荷载的作用,由于单次荷载作用历时短,孔隙水来不及消散,因而可将其视为不排水过程。第1次加载过程前,土体的前期固结压力为p′c,孔隙水压力为u0,所承受总压力为p=p′c+u0。在循环荷载作用下不排水固结时,孔隙水压力u为:
u=p-p′
(25)
4 计算流程
计算流程图如图5所示。
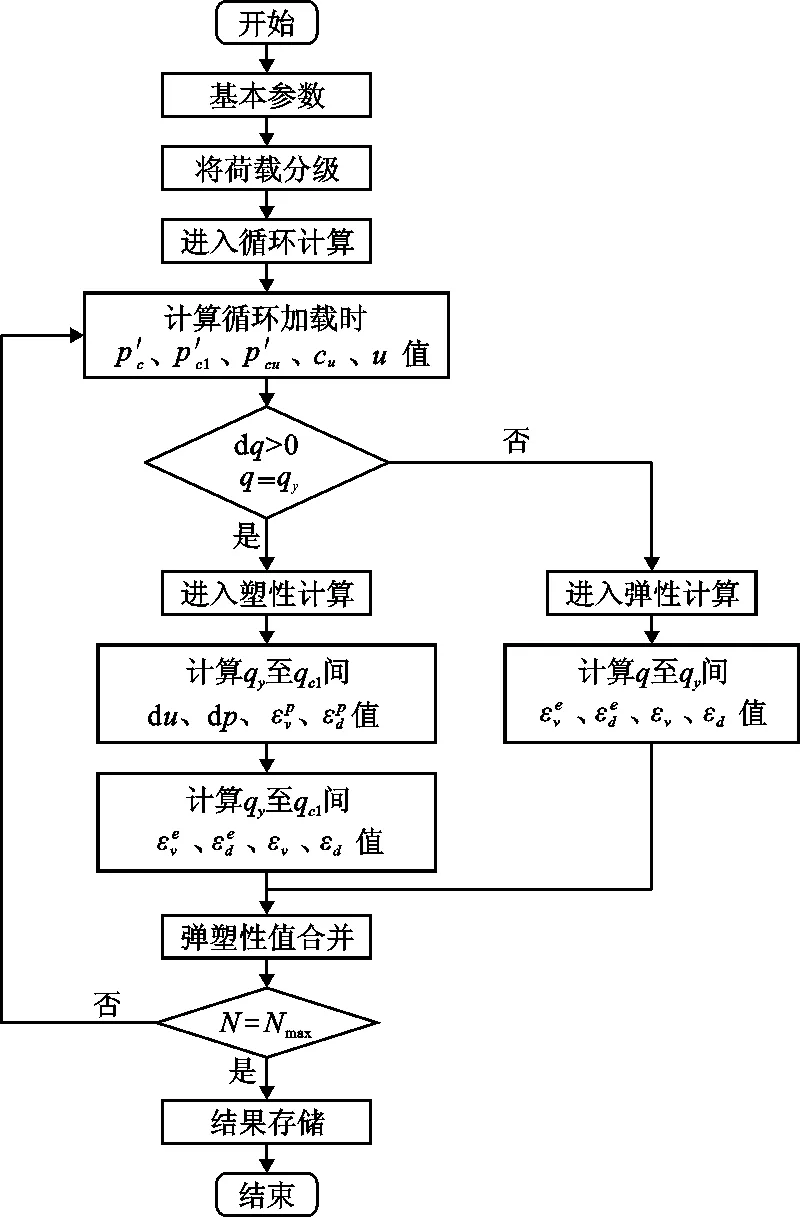
图5 计算流程
主要计算过程如下:
(1)通过基本土工试验与三轴试验,计算修正剑桥模型参数M、λ、κ以及θ0、Θ值;初始应力p′0、q值,循环应力值qc;
(2)将初始状态值p′0、q、qc代入公式(20)计算第1次循环加载到qc的p′y,1值;计算第1循环加载后的p′c1,1值;
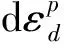
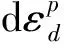

(6)循环(5)直到N达到循环破坏次数;
(7)计算结果存储。
5 例 证
为验证本研究提出的循环荷载下K0固结土体动力本构模型的正确性,分别选取2个案例进行计算分析,具体验证情况如下。
5.1 Niigata砂
案例1选取文献[22]中的计算案例。Niigata砂土样为人工冻结法取得的未扰动样,进行了双向循环加载、应力控制、不排水三轴试验。因无本文计算参数的文献资料,故选用了与Niigata砂位置相近的Toyoura砂的物理力学参数作为计算参数[23],具体材料基本性质及计算参数见表1。

表1 案例1 Niigata砂的基本性质及计算参数
不同相对密度试样的计算结果与试验结果比较如图6所示。

图6 案例1不同相对密度试样的计算结果与试验结果比较
图6中实线和虚线分别表示相对密度Dr为78%和54%时的计算结果拟合曲线。根据Yoshimi等[22]的试验结果,应变值超过5%以后的循环次数与破坏时的循环次数在低循环应力比时相差较小,在图6中试验值取应变为5%的循环次数,计算值取砂土破坏时(应变大于5%)的循环次数。从图6可以看出:(1)在相对密度为78%时,本文计算结果与文献[22]中计算结果吻合度较高,循环次数随循环应力比的减小而增大;(2)在相对密度为54%时,本文计算结果与文献[22]中计算结果基本吻合,循环次数同样随循环应力比的减小而增大;(3)根据曲线向前延伸的趋势分析,当循环应力比小于某一数值时,土体不再破坏,即存在临界循环应力比。因而,本文提出的循环荷载下K0固结土统一硬化模型对于砂土的计算具有较高精度。
5.2 杭州萧山黏土
案例2选自文献[24]中的计算案例。黏土为杭州萧山原状土样,土样直径为39.1 mm,高度为80 mm。试样采用真空抽气饱和,然后等向固结24 h。循环荷载为对称型正弦波荷载,频率为1 Hz,试验过程中试样不排水。试验仪器为HX-100型气压伺服式多功能动三轴仪,采用应力控制方式。修正剑桥模型参数参考张庆山等[25]选取,计算参数见表2。

表2 案例2黏土性质及计算参数
不同应力比的计算结果与试验结果比较见图7。

图7 案例2不同应力比的计算结果与试验结果比较
从图7可以看出:(1)采用本文计算方法获得的循环次数与轴向应变的关系曲线与试验结果比较吻合,循环应力比值越小,两者吻合程度越高;(2)在同一循环应力比时,随循环次数的增加,应变计算值与试验值更为接近;(3)在3种循环应力比作用下,土体破坏时的循环次数计算值与试验值比较接近。本文提出的循环荷载下K0固结土统一硬化模型同样适用于黏土计算,且计算所需参数仅为10个,少于文献[24]所需数目,试验参数可以通过基本土工试验和三轴试验获得。
综合上述2个案例对比结果可以认为,本研究提出的本构模型可以用于海洋K0固结黏土与砂土在循环荷载工况的计算,且具有参数少的优势。
6 结 论
(1)基于剑桥本构模型,结合经典弹塑性理论和Collins的热力学理论,选用耗散功作为硬化参量,推导了适用于黏土和砂土的统一硬化模型。
(2)考虑在动荷载作用下,屈服面向内移动缩小,至一定应变时土体屈服破坏,同时通过将循环荷载对天然固结土的扰动视为主应力轴的旋转,引入屈服面收缩参数Θ,提出了循环荷载下海洋K0固结土的统一硬化动力本构模型。
(3)通过两个案例的计算分析,验证了本文研究提出的统一硬化参量动力本构模型的可行性,该动力本构模型具有较高精度,计算土工参数少、容易获取且物理意义明确。
