广东省高层建筑抗震设计用地震动功率谱

崔 威 ， 冼剑华 ， 苏 成 ，2

（1. 华南理工大学 土木与交通学院， 广州 510640； 2. 华南理工大学 亚热带建筑科学国家重点实验室， 广州 510640）

0 引言

对于高层和超高层建筑等大型复杂结构， 地震作用往往是最重要的设计荷载， 因此结构设计的安全性依赖于地震作用计算的合理性。 目前我国 《建筑抗震设计规范》（GB 50011-2010）[1]所推荐的高层建筑地震作用计算方法包含振型分解反应谱法和时程分析法。 振型分解反应谱法能够反映地震动的随机特性， 但不能反映地震作用的全过程， 而且规范所推荐的CQC 组合公式是在一定假定[2-3]下推导得到的， 这些假定会对高层和超高层建筑结构的地震作用计算带来一定的影响[4]。 时程分析法能够反映地震作用的全过程， 但不能反映地震动的随机特性， 因此该方法一般作为振型分解反应谱法的补充计算方法。 鉴于上述问题，有必要采用真正意义的随机振动分析方法进行高层和超高层建筑结构的地震作用计算。

时域显式随机模拟法[4]是一种高效准确的非平稳随机振动分析方法， 该法适用于大型复杂结构的抗震计算， 且容易被工程设计人员所接受，目前已被编入广东省《高层建筑混凝土结构技术规程》（DBJ 15-92-2013）[5]， 以下简称 “2013 版省《高规》”。 近年来， 针对非线性隔震结构地震作用计算所发展的非线性时域显式随机模拟法[6]也编入新修订的广东省 《高层建筑混凝土结构技术规程（送审稿）》（DBJ 15-92-2020）[7]， 以下简称 “2020版省《高规》”。 由此可见， 采用实用随机振动分析方法进行高层建筑结构抗震设计已在工程界受到广泛重视。

振型分解反应谱法的输入条件是反应谱， 而随机振动分析方法的输入条件通常为地震动功率谱。 为保证随机振动分析方法和振型分解反应谱法的输入条件一致， 设计地震动功率谱必须与设计反应谱完全等价。 如此一来， 随机振动分析方法的计算结果才可与振型分解反应谱法的计算结果进行比较， 并为实际工程设计提供参考。 因此，获取与规范反应谱完全等价的地震动功率谱是随机振动分析方法能够在工程设计中推广应用的重要基础。

本文基于新修订的2020 版省《高规》， 利用直接迭代方法获得与该规范反应谱完全等价的地震动功率谱； 进而利用非线性函数拟合技术， 得到等价地震动功率谱的拟合公式； 最后验证拟合后等价地震动功率谱与规范反应谱的等价性。 此外，本文还系统研究了不同功率谱初始形式以及不同结构阻尼比对所得等价地震动功率谱的影响。

1 设计加速度反应谱

2020 版省《高规》对 2013 版省《高规》的设计反应谱进行了修改， 新的设计反应谱是由华南理工大学建筑设计研究院根据6000 多条实际地震波统计分析得到的[8-10]。 2020 版省《高规》的设计加速度反应谱如下式所示[7]：

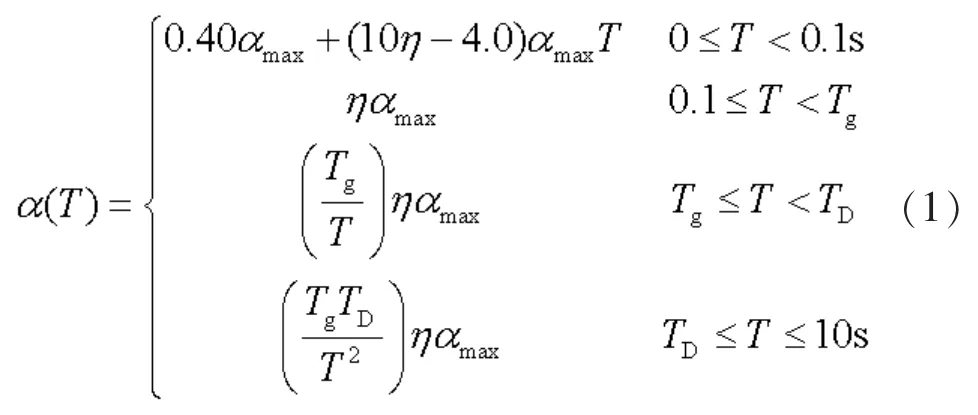
式 （1）中 α 为水平地震影响系数； αmax为水平地震影响系数最大值， 它的取值与场地类别有关， 对于II 类场地其取值见表1， 而对于其它类别场地其取值见文献 [7]； T 为结构自振周期； Tg为特征周期， 取值见表 2； TD=3.5 s； η 为阻尼调整系数，如下式所示：

式 （2）中 ζ 为结构阻尼比。

当考虑设防烈度 7 度、 多遇地震、 阻尼比0.05 及设计地震第一分组时， 不同场地类别下的设计加速度反应谱曲线如图1 所示。 从图中可以看出， 随着场地类别的提高， 设计加速度反应谱曲线平台段的高度和宽度均有所增大。

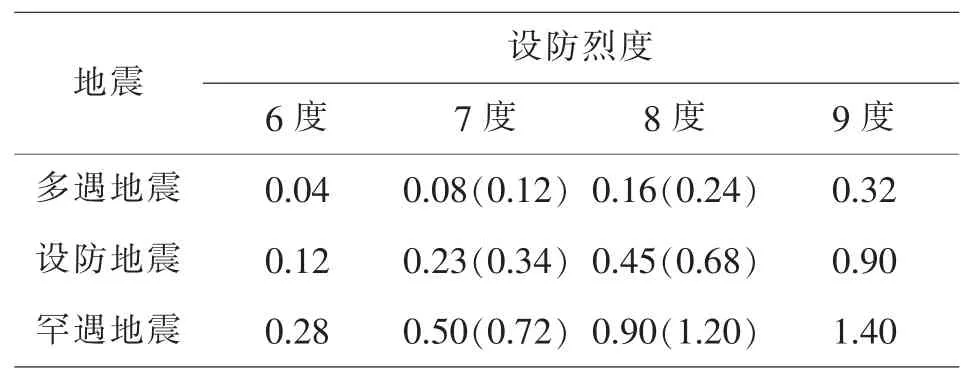
表1 水平地震影响系数最大值αmax （II 类场地）Table 1 Maximum value of horizontal seismic influence coefficient αmax （Site-class II）

表2 特征周期Table 2 Characteristic period

图1 设计加速度反应谱Fig.1 Acceleration response spectrum for design

2 等价地震动功率谱的确定

考虑地震动的非平稳随机特性， 地面加速度随机过程X（t）可以表达为[11]

式（3）中 x（t）为平稳随机过程； g（t）为均匀调制函数， 用来考虑地面加速度随机过程的强度非平稳特性， 可以表示为

式 （4）中 c 为衰减系数； t1和 t2分别为强震平稳段的起始和终止时间。 均匀调制函数参数的取值如表 3 所示[12]。

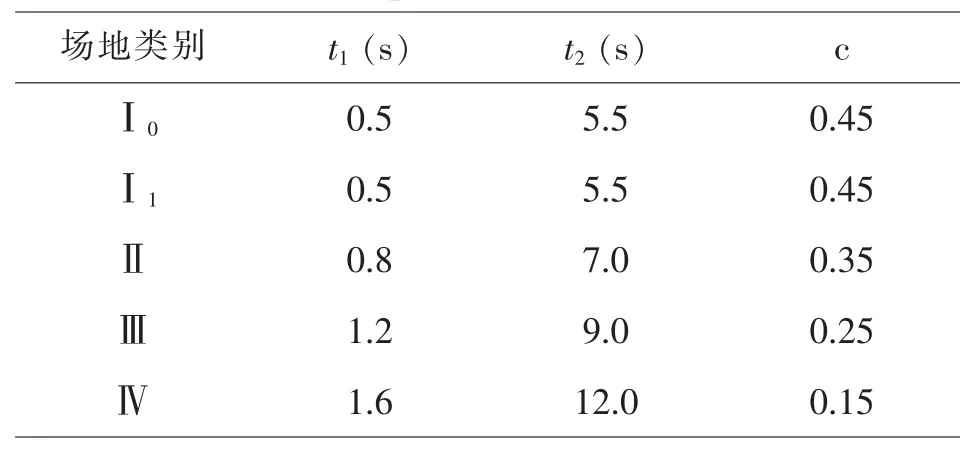
表3 均匀调制函数参数的取值Table 3 The values of parameters of modulation function

假定平稳随机过程x（t）的功率谱密度函数为S（f）， 可采用谐波合成法[13]对 x（t）进行随机采样， 其中第j 个时程样本可以表示为

式（5）中M 为地面加速度时程的样本数； N 为频率划分段数； Δf=（fmax-fmin）/N 为谐波分量的频率间隔；fmax和fmin分别为截断最大频率和截断最小频率， 分别取值为 30 Hz 和 0.04 Hz； fk==fmin+（k-0.5）Δf 为第k 个谐波分量的频率； Φk,j为服从 [0，2π]均匀分布的随机变量。 Δf 的取值应不大于 1/td[14]， 其中 td为地面加速度持续时长， 考虑到td可能取到50 s，故取 Δf=0.02 Hz， 此时 N=1498。

文献[14]给出了功率谱密度函数S（f）和反应谱函数 α（T）（T=1/f）之间的近似转换关系， 如下式所示：

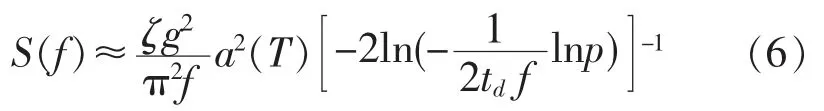
式 （6）中p 为地震作用反应不超过反应谱值的概率， 一般取 p≥0.85； g 为重力加速度， 取为9.8 m/s2。

以式（6）作为功率谱密度函数 S（f）的初始形式， 利用式（5）生成大量平稳随机过程的时程样本xj（t）， 再根据式（3）得到大量非平稳地面加速度随机过程的时程样本 Xj（t）（j=1，2，…，M）。 计算在这些地面加速度样本作用下单自由度体系的平均加速度反应谱 α"（T）， 并与规范加速度反应谱 α（T）进行比较， 按下式计算相对误差：

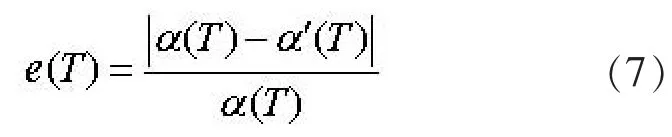
若相对误差e（T）的最大值大于给定的误差容许值ε， 取为5%， 则按下式对功率谱密度函数进行修正：

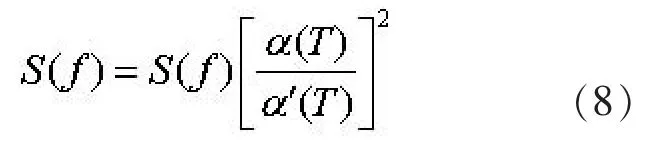
重复上述步骤， 直至相对误差e（T）的最大值小于给定的误差容许值ε， 才停止迭代计算。 此时获得的S（f）可认为是与规范反应谱完全等价的地震动功率谱。

3 等价地震动功率谱拟合

采用第2节的方法可以获得与规范反应谱等价的离散地震动功率谱， 为了方便工程人员直接应用， 下面进一步利用非线性函数拟合技术得到离散等价地震动功率谱的拟合表达式。 将式（1）代入式（6）可得功率谱的分段拟合公式为

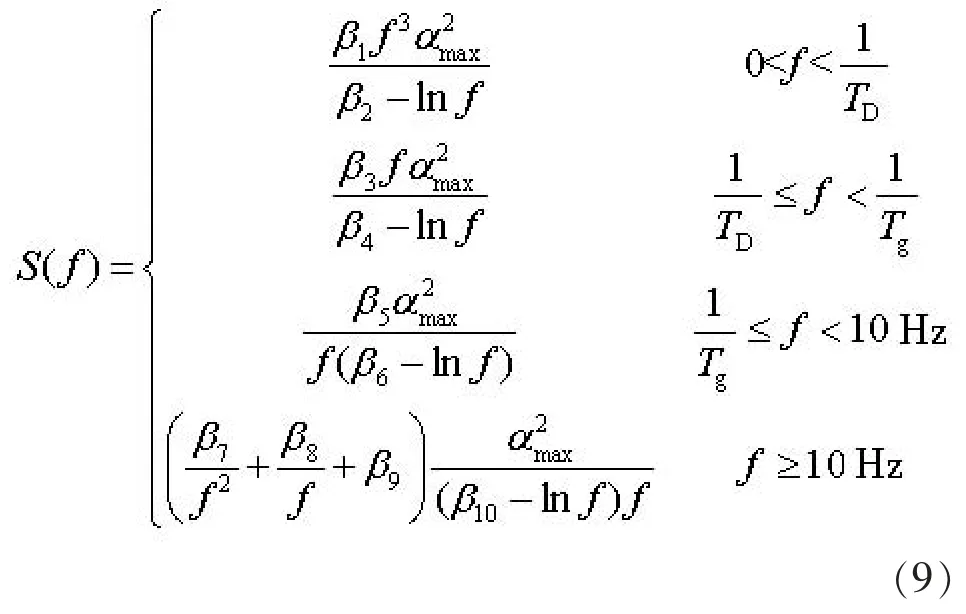
式（9）中 β1， β2， …， β10为待求的拟合参数。

对于设防烈度7 度、 多遇地震、 阻尼比0.05、II 类场地及设计地震第一分组的情况， 基于式（9）拟合得到的等价地震动功率谱和拟合前的离散等价地震动功率谱如图2 所示。 从图中可以看出，拟合功率谱和离散功率谱总体吻合良好， 但在第一分段拟合功率谱出现了负值， 与实际不相符。数值试验表明， 拟合公式第一分段采用指数函数形式更为合理， 则功率谱的分段拟合公式可以改写为

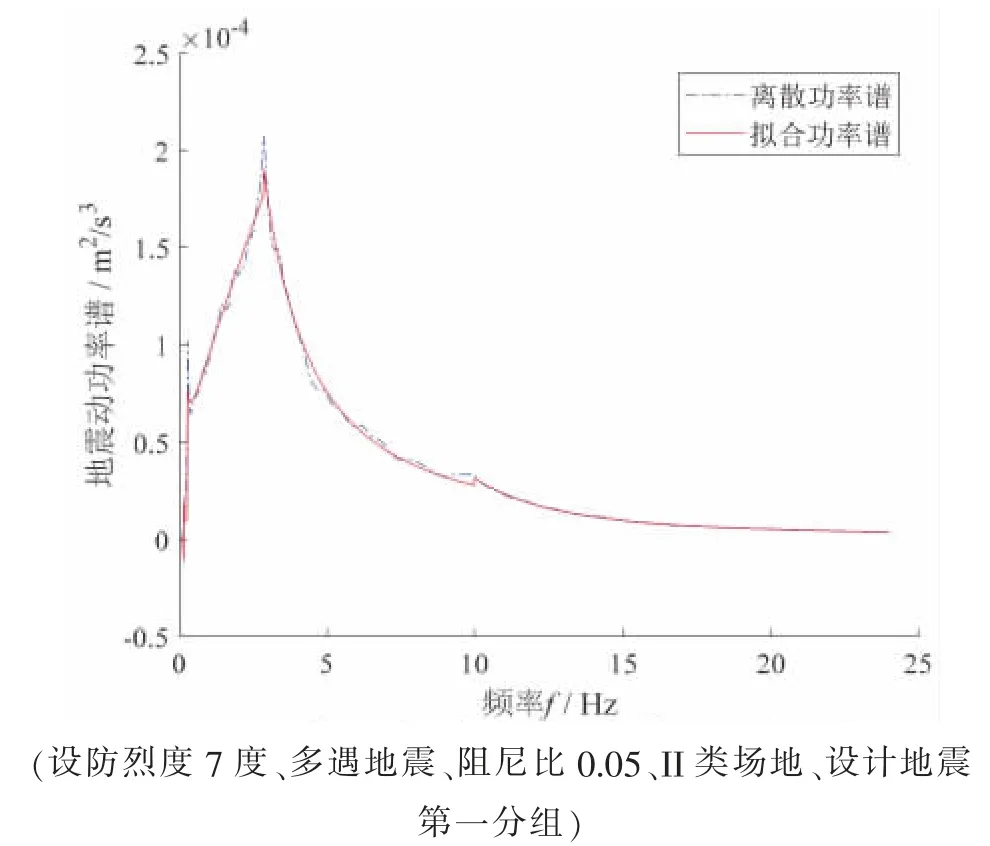
图2 基于式（9）拟合的等价地震动功率谱Fig.2 Equivalent ground motion power spectrum fitted based on equation（9）

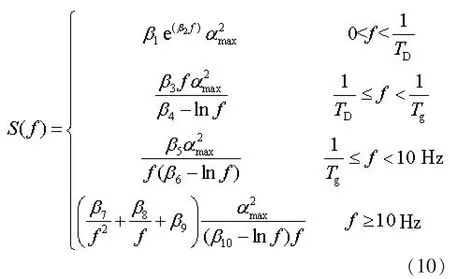
基于式（10）拟合得到的等价地震动功率谱和拟合前的离散等价地震动功率谱如图3 所示。 从图中可以看出， 拟合功率谱和离散功率谱在各个分段均吻合良好， 且在第一分段没有出现负值。值得一提的是， 拟合功率谱有效削弱了离散功率谱在 f=0.286 Hz（对应 T=TD=3.5 s） 处的突起， 使等价地震动功率谱更具合理性。 对于阻尼比0.05 及II 类场地的情况， 各设计地震分组对应的等价地震动功率谱拟合参数值见表4。 对于其它阻尼比及场地类别的情况， 等价地震动功率谱的拟合参数值见文献[7]。

为检验等价地震动功率谱与设计加速度反应谱之间的等价性， 基于拟合后的等价地震动功率谱， 采用谐波合成法生成大量的地面加速度时程样本， 进而获得单自由度体系的平均反应谱， 即模拟加速度反应谱。 以图3 所示拟合功率谱为例，所得模拟加速度反应谱与设计加速度反应谱如图4所示。 从图中可以看出， 二者吻合良好， 说明拟合功率谱与设计加速度反应谱在所考虑的周期范围内是完全等价的。

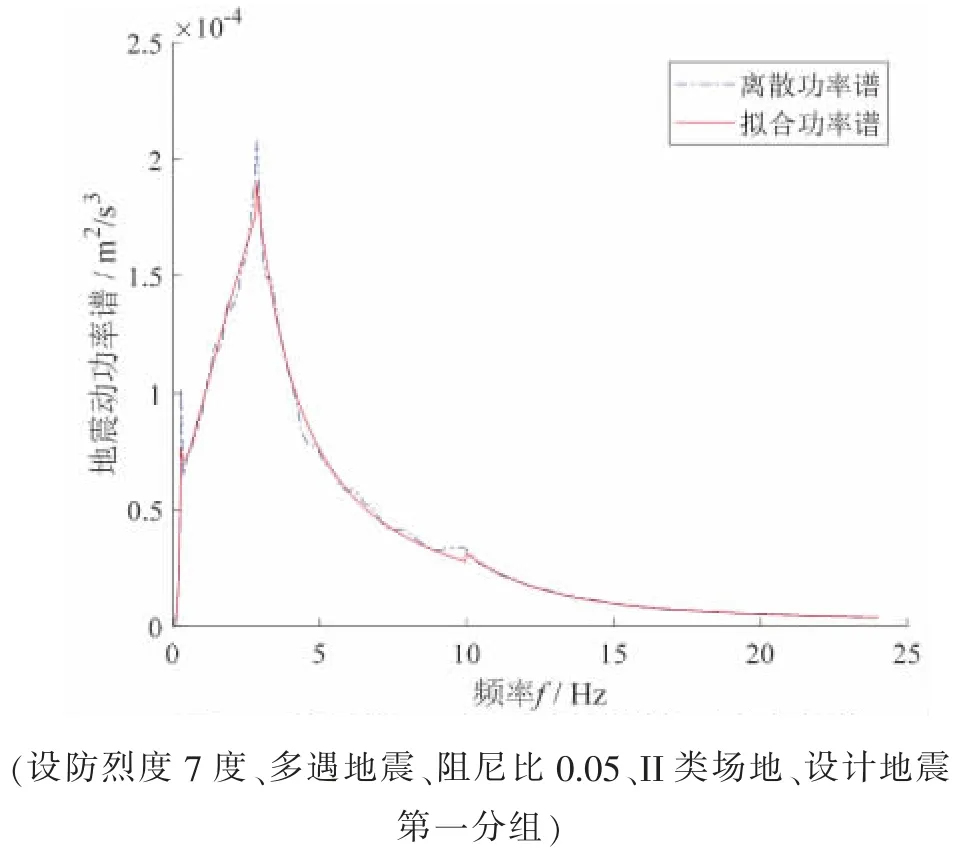
图3 基于式（10）拟合的等价地震动功率谱Fig. 3 Equivalent ground motion power spectrum fitted based on equation （10）

表4 等价地震动功率谱拟合参数值（阻尼比 0.05、 II 类场地）Table 4 The values of fitted parameters of equivalent ground motion power spectrum （Damping ratio 0.05，site-class II）

图4 模拟加速度反应谱Fig.4 Simulated acceleration response spectrum

4 等价地震动功率谱一致性验证

本节以设防烈度 7 度、 多遇地震、 阻尼比0.05、 II 类场地及设计地震第一分组情况下所获得的等价地震动功率谱为例， 分别研究不同功率谱初始形式以及不同结构阻尼比对所得等价地震动功率谱的影响。

4.1 功率谱初始形式的影响

为检验所得等价地震动功率谱对于不同的功率谱初始形式具有一致性， 分别以式（6）所示功率谱和白噪声功率谱作为等价地震动功率谱的初始形式进行迭代计算， 所得等价地震动功率谱如图5所示。 从图中可以看出， 基于不同的功率谱初始形式所获得的等价地震动功率谱吻合良好， 说明等价地震动功率谱的获取与功率谱初始形式的选取无关。 此外， 当以式（6）功率谱作为初始功率谱时， 迭代收敛所需次数为4 次， 而当以白噪声功率谱作为初始功率谱时， 迭代收敛所需次数为6次， 说明选取更接近收敛后等价地震动功率谱的功率谱初始形式可以更快收敛。

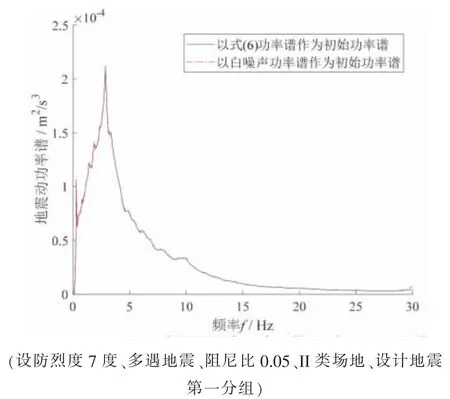
图5 不同功率谱初始形式对应的等价地震动功率谱Fig.5 Equivalent ground motion power spectrum corresponding to different initial forms of power spectrum

4.2 结构阻尼比的影响

为检验不同结构阻尼比对所得等价地震动功率谱的影响， 分别以不同的结构阻尼比（0.03、0.035、 0.04、 0.045、 0.05、 0.055、 0.06、 0.065 和0.07）获取等价地震动功率谱， 如图6 所示。 从图中可以看出， 以阻尼比为0.05 所对应的等价地震动功率谱为基准， 其它阻尼比所对应的等价地震动功率谱与该基准吻合良好， 说明不同结构阻尼比（0.03～0.07）所对应的等价地震动功率谱具有一致性。 这是合理的， 因为地震动本质上与结构阻尼是没有关系的。

5 结语

图6 不同结构阻尼比对应等价地震动功率谱Fig.6 Equivalent ground motion power spectrum corresponding to different structural damping ratios

采用真正意义的随机振动分析方法进行高层或超高层建筑结构的抗震设计已经引起了工程界的广泛重视， 而获取与规范反应谱完全等价的地震动功率谱是随机振动分析方法能够在工程领域推广应用的重要基础。 本文基于新修订的2020版省 《高规》， 利用直接迭代方法获得与新修订的设计加速度反应谱完全等价的地震动功率谱， 并采用非线性函数拟合技术获得等价功率谱的拟合公式。 数值验证表明， 拟合后的等价功率谱与规范反应谱是完全等价的。 本文还对不同功率谱初始形式以及不同结构阻尼比对所得等价地震动功率谱的影响展开研究。 结果表明， 等价地震动功率谱对于不同的功率谱初始形式以及不同的结构阻尼比（0.03-0.07）具有一致性。