考虑筋土界面相互作用的加筋路基变形特性分析
2021-04-23戴敬敬
戴敬敬
(上海公路桥梁(集团)有限公司, 上海 200433)
0 引言
在各类软土地基上, 由于承载力不够, 在修建公路、 铁路等基础设施时会造成沉降过大影响施工以及使用等问题。 面对此种情况, 在各类工程中采用土工合成材料对不同结构进行加固的方法已经得到了广泛的运用[1-2]。
目前已有许多学者对加筋土结构进行了理论分析。 赵明华[3]通过改进传统土柱模型, 计算分析了考虑土拱效应的土工格室加筋路堤的受力变形。孙亮富[4]设计了单向网格状带齿加筋, 初步分析了此种三维立体加筋砂垫层的作用机理。 还有很多学者从理论角度对加筋地基进行了相关研究。 陈昌富[5]分析计算了筋材-桩体组合的地基极限承载力, 并通过实际工程实例对比计算。 Maheshwari[6]提出条形荷载下土工合成材料加筋软弱地基的力学模型, 分析了土层的相对刚度, 梁的相对抗弯刚度以及受力区域等参数的影响。 此外, 在加筋土结构动力响应方面, Calvarano[7]从数值计算角度采用ABAQUS 软件, 对混合基础上未铺设路面层的加筋道路结构进行分析, 得到了循环荷载作用下的动力响应。 宋广[8]基于加筋路基在交通荷载作用下的变形特点, 对路面变形和路基加筋效果进行了参数影响分析。
在此基础上, 学者们针对不同的计算方法对地基上加筋结构变形的影响进行了研究。 王陶[9]在进行了加筋道路计算时考虑了薄膜效应, 并得出了假定薄膜挠度很小的平衡微分方程, 得到加筋道路体系一般解。 赵明华[10]针对土工格室在软土路基中的受力变形特点, 将其简化为连续长梁, 并建立了土工格室加筋体的挠曲变形方程。 边学成[11]利用Pasternak 模型分析了路基填料与地基土之间的剪切作用, 并对土工格室加筋体进行了分析。Ghosh[12]将软土上荷载传递平台的物理模型理想化为Kerr 地基上的薄膜加筋Timoshenko 梁, 得到了一个较为精确的分析模型。
综上所述, 本文考虑筋材在基层中的相互作用, 研究加筋路基中筋材及参数、 界面摩阻系数、基层参数及水平荷载等因素的影响, 分析了不同参数下路面结构及筋材的变形特征, 对采用加筋路基结构的实际工程具有一定的参考价值。
1 计算模型与计算公式
1.1 模型建立
图1 为本文所采用的简化模型示意图, 采用Timoshenko 梁模拟路面结构, Pasternak 剪切层模拟基层特性; 土工合成材料采用线弹性模型模拟土工合成材料特性。
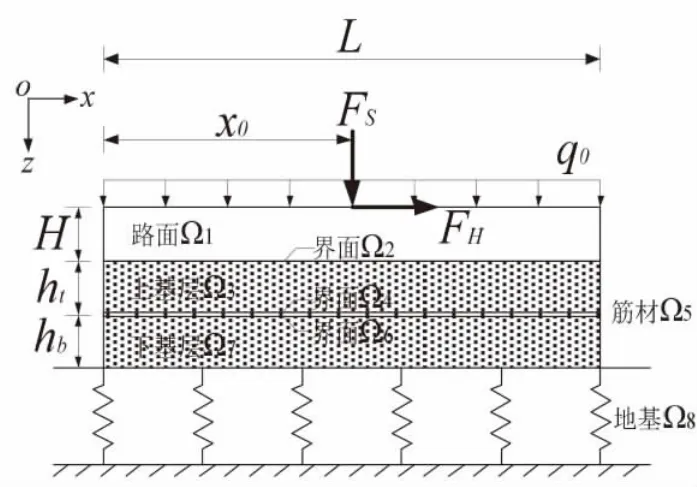
图1 简化模型Fig.1 Simplified model
在路面上施加均布荷载q0与一竖向集中荷载FS以模拟车辆荷载, 同时在作用点处施加一水平荷载以模拟制动荷载。 假设结构整体长为L, 宽为B, 路面结构厚度为H, 上下基层厚度分别为ht与hb。 如图所示, 将路面、 筋材及基层所占空间记为Ωi(i=1,3,5,7); 将路面与基层、 基层与筋材的接触界面分别记为 Ωj(j=2,4,6); 将软土地基记为Ω8。
1.2 位移假定及受力分析
根据图1 中的局部坐标, w 为竖向位移(z 方向), u 为水平位移(x 方向), θ 为截面转角。 可得路面结构中局部坐标(x1,z1)和上部基层中局部坐标(x2,z2)处的水平位移与竖向位移分别为:
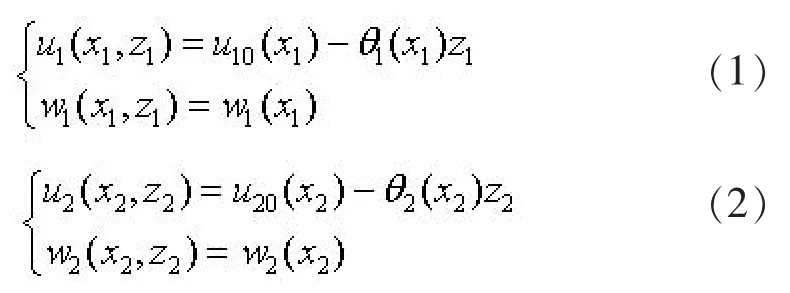
由于土工格栅的厚度较小, 筋材中横坐标处的水平位移和竖向位移分别为 u30(x3)和 w2(x3)。
下部基层中局部坐标为 (x4,z4)处的水平位移与竖向位移分别为:
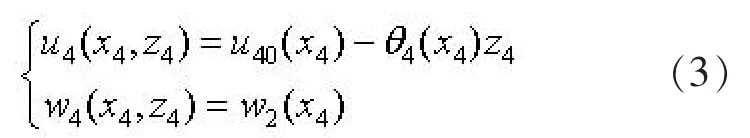
结合式(1)、 (2)可以计算出路面与基层的相对滑移ur1、 筋材与上、 下基层接触面间的相对滑移ur2与ur3, 及下部基层与地基间的相对水平位移ur4分别为:
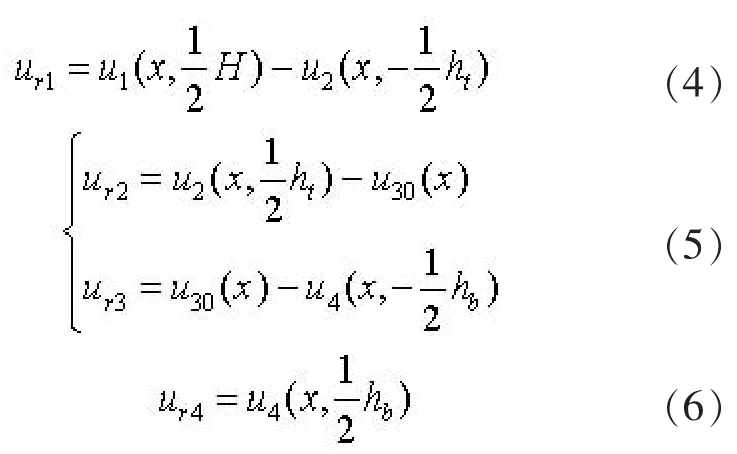
根据文献[13]可知, 基层中的剪应力τ 可以表示为:
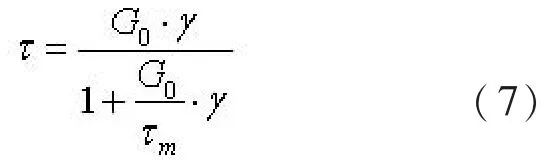
式 (7) 中τm为基层极限剪力, G0为初始剪切模量。
其中, 剪切刚度G 为关于剪切应变的一阶导数:
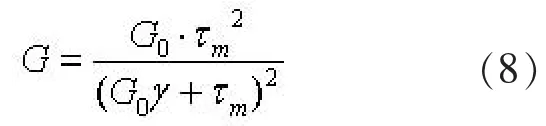
由参考文献[14]中可知竖向反力公式如下:
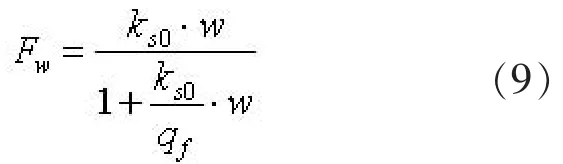
式(9)中, ks0为初始反力系数, qf为地基极限承载力, w 为竖向位移。 由此可得其切向反力系数ks:
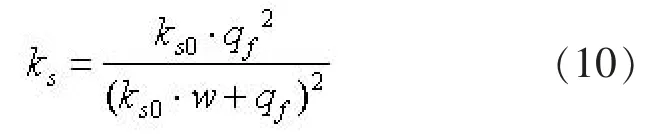
对于层间摩阻力f, 其公式为:
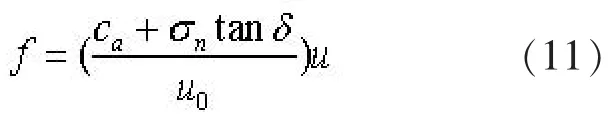
式(11)中, ca为界面土体黏聚力, σn为界面正应力,δ 为路面-基层界面及筋土界面摩擦角, u0为临界相对滑移量, u 为界面相对滑移。 由于考虑了各层的轴向变形, 界面相对滑移的值较小, 假设界面相对滑移u 保持在临界滑移值u0内, 并使各层间的水平摩阻系数(x=1~4)。 由此可得:
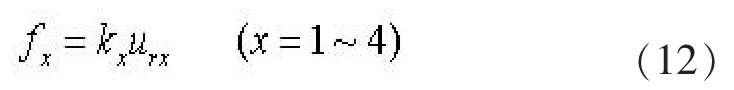
式(12)中, f1为路面与基层间水平摩阻力, f2、 f3为筋材与上、 下基层间水平摩阻力, f4为下部基层与地基间水平摩阻力。
路面与基层间的相互作用力F"计算如下为:
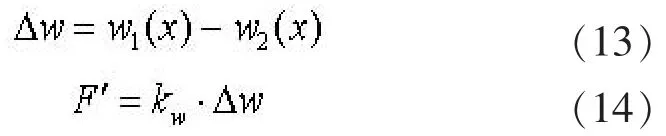
式(14)中 kw接触面拉压刚度。 结合以上公式, 可列出虚功方程如下:
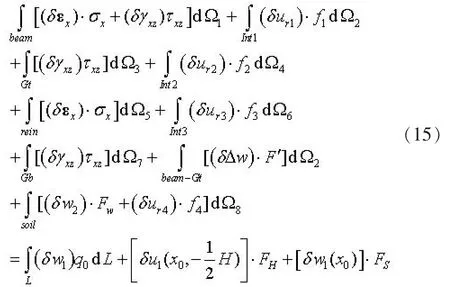
2 方程求解
2.1 单元形函数

图2 局部坐标与节点Fig.2 Local coordinates and the nodes
如图2 所示, 采用的有限元三次插值形式,并在数值运算时采用减缩积分法。 L0为单元长度,采用三次插值进行计算, 得到插值函数如下:
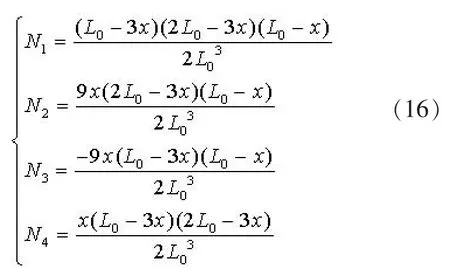
将节点的位移向量Ψn (n=1~4) 表示如下:
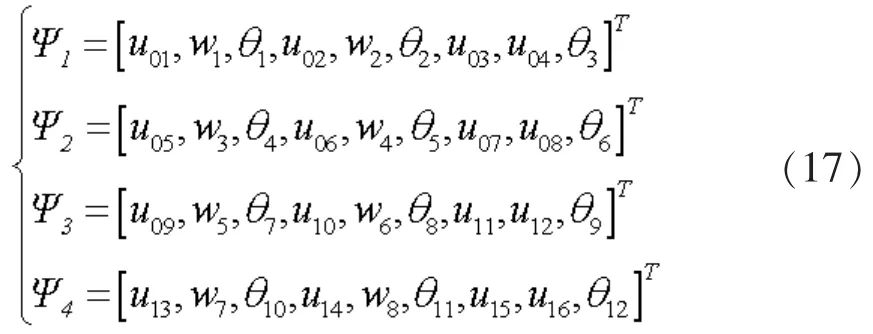
将式(17)合并后得到单元自由度向量:
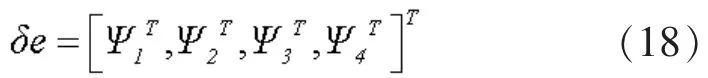
根据图2 可得, 路面梁单元的水平位移、 竖向位移以及截面转角形函数如下:
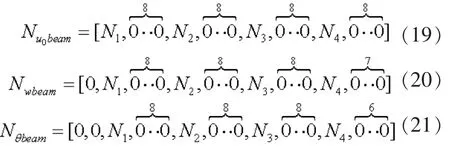
同理, 基层单元的各形函数分别为:

下部基层单元的各位移和截面转角形函数为:

因此, 其相对竖向位移形函数为:
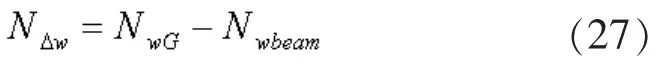
同理, 其应变形函数为:
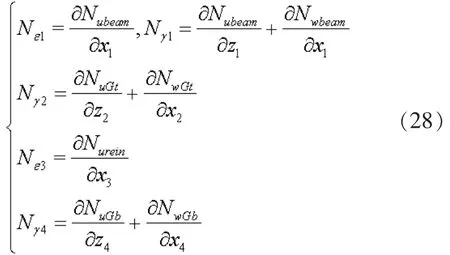
式中 Nε1为路面结构内正应变, Nγ1为其剪应变; 仅考虑基层中的剪切效应, Nγ2、 Nγ4分别为上、 下部基层中的剪应变; Nε3为筋材应变。
由式(4)、(5)、(6)以及式(25)、(26)可得界面相对位移形函数:
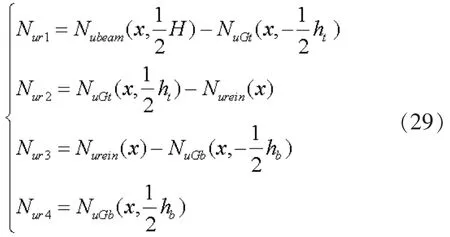
2.2 公式求解
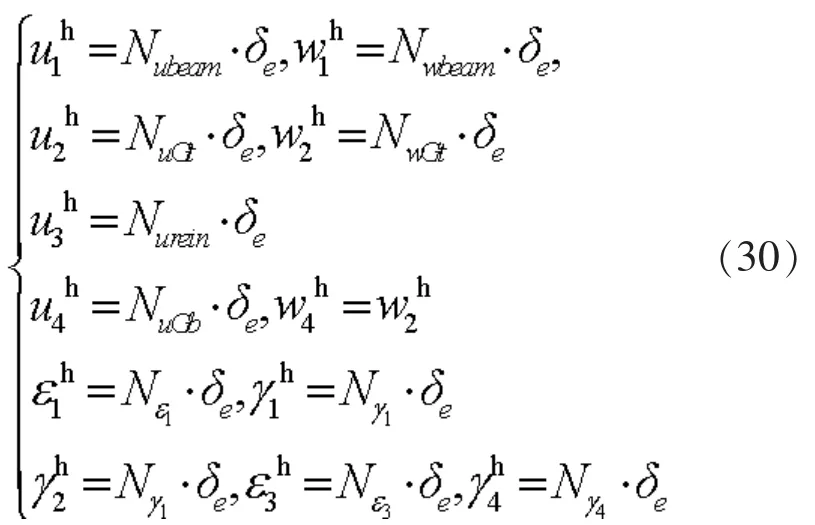
上式为位移和应变的插值函数, 上边h 表示有限元近似, 将公式离散后得到单元残值向量:
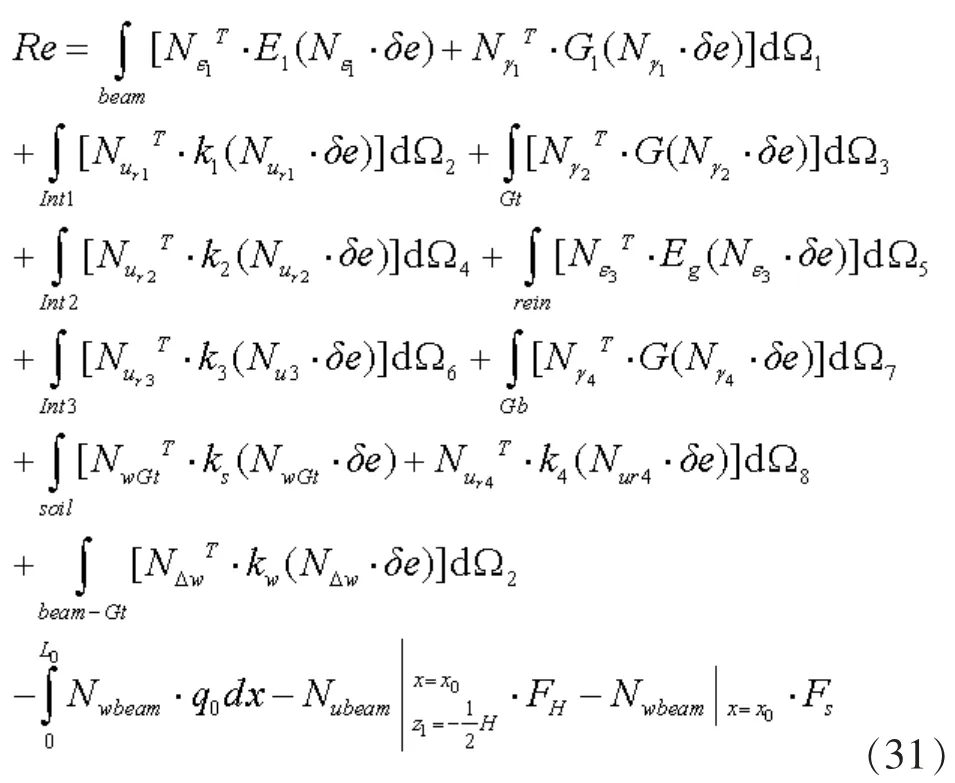
根据式(31), 可得单元切向刚度矩阵:
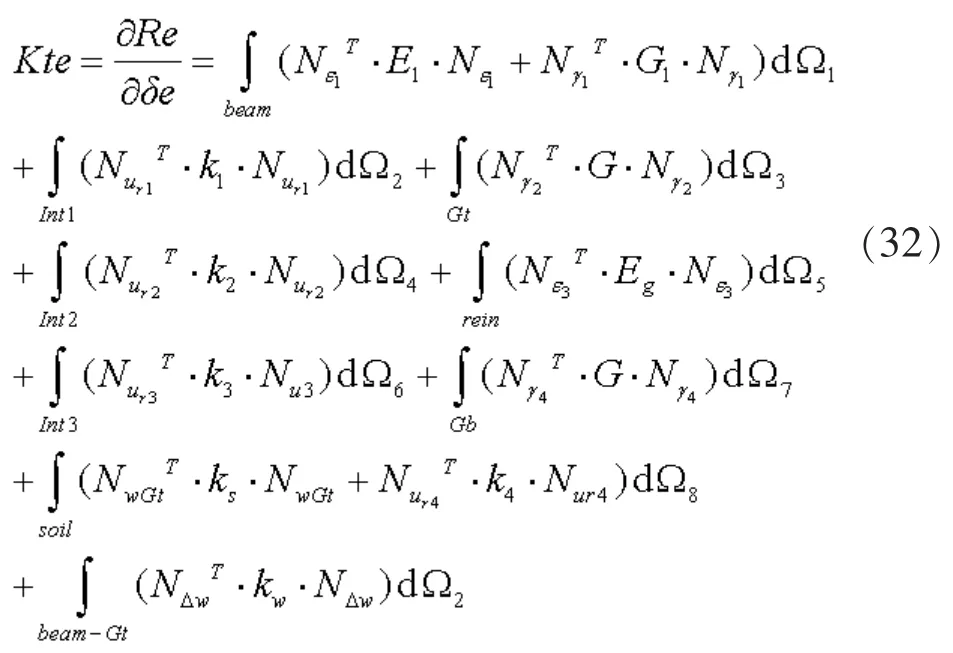
3 计算分析
3.1 算例分析
本文将计算模型退化为Winkler 地基模型(如图3), 并将其计算结果与文献[15]结果进行对比。由图 4 可知, 划分结构 20 单元, 即 61 节点计算得到的结果与文献[20]相近, 验证了本文计算模型的可靠性。
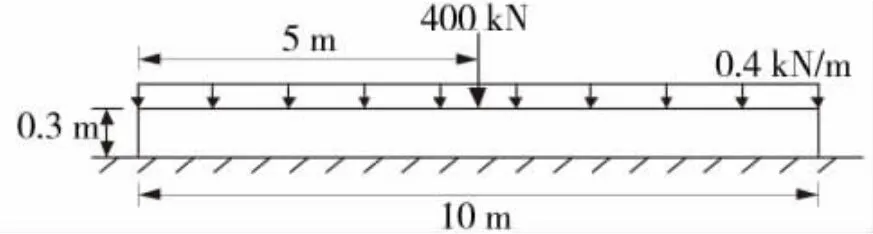
图 3 Winkler 地基上 Timoshenko 梁Fig.3 Timoshenko beam on Winkler foundation
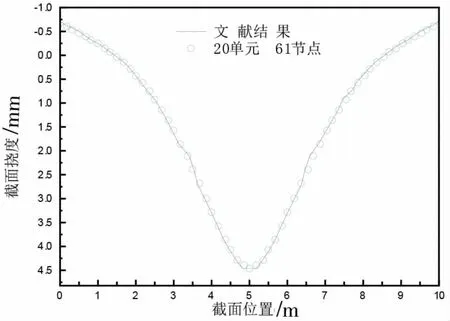
图4 挠度结果对比Fig.4 Comparison of deflections for different cross-sectional positions
3.2 参数分析
运用本文推导所得的模型对整体结构进行分析, 初始参数值见表1。
3.2.1 筋材参数的影响
图5 给出了不同筋材基层间摩阻系数和抗拉模量的路面跨中挠度曲线。 相比不加筋的情况,铺设筋材能够有效的减小跨中挠度。 随着抗拉模量与摩阻系数的增大, 其跨中截面挠度分别减小了22.75%和34.15%。 这表明在基层中铺设土工合成材料可以有效地减小路面跨中界面挠度, 增强基层抗变形能力。 而采用抗拉模量较大的筋材并增大筋材与基层间的摩擦阻力, 可以减小筋材与上、 下基层接触面间的相对滑移, 分散和抵消局部荷载, 有效提高加筋路基的承载力。
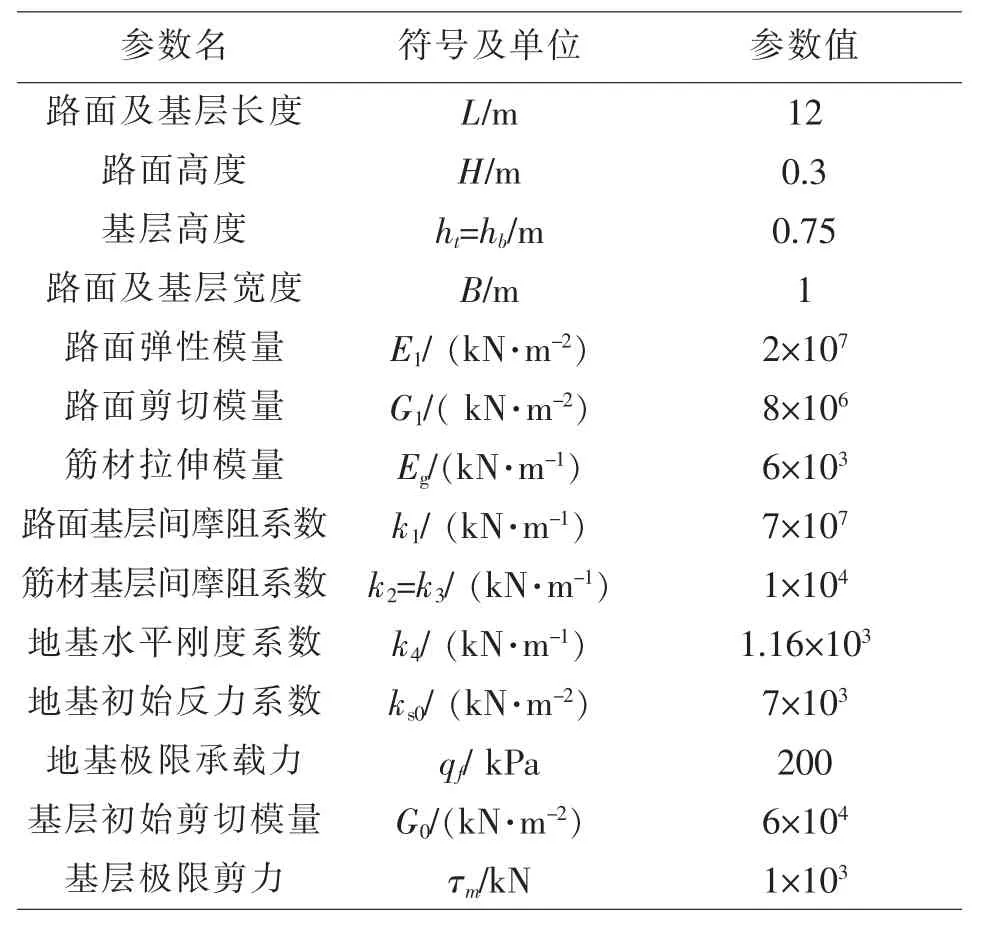
表1 数值分析计算参数取值Table 1 Values of parameters for numerical analysis
图6 给出了跨中作用1000 kN 竖向荷载时筋材与上部基层间的摩擦阻力。 当摩阻系数为1×104kN·m-1, 筋材抗拉模量增大时, 跨中位置右侧界面摩阻力逐渐减小, 左侧界面摩阻力逐渐增大, 而后曲线趋于平缓。 抗拉模量 Eg 由 6×103kN·m-1增大为原本的5 倍与10 倍时, 界面摩阻力最大值分别减小了37.74%与55.99%, 近端点处摩阻力则向正值增大, 表明筋材与土相对位移略有增大; 而当筋材抗拉模量保持在 6×104kN·m-1时, 摩阻系数增大为原本的2 倍与3 倍时, 界面摩擦阻力整体有所增大, 其极值分别增大了 178.57%与374.61%。 由此可看出, 随着筋材抗拉模量的增大,界面间的相对滑移以及摩擦阻力减小, 自身抗拉性能所提供的加筋效果更明显; 而增大摩阻系数可以显著增大界面摩擦阻力, 更好提升筋材的加筋效果。
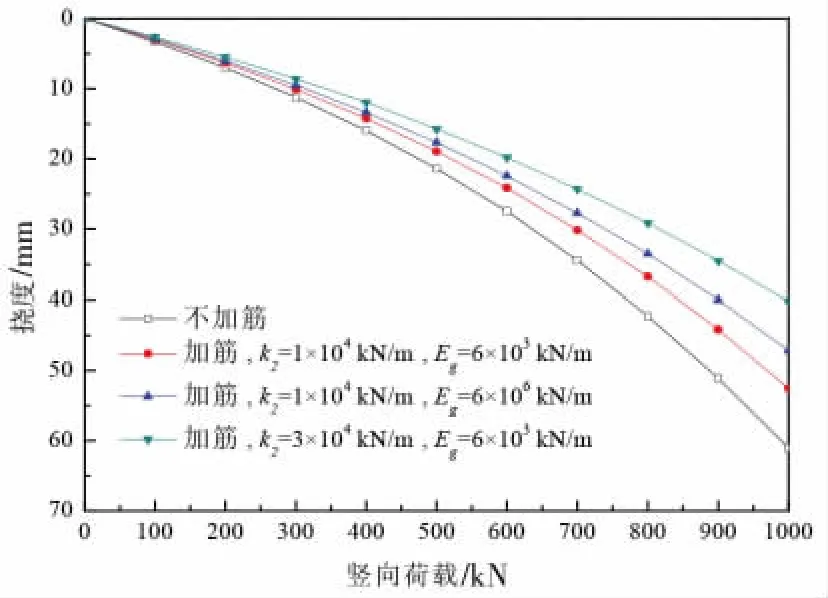
图5 不同筋材参数对路面挠度的影响Fig.5 Influences of different parameters of geosynthetic on pavement deflections
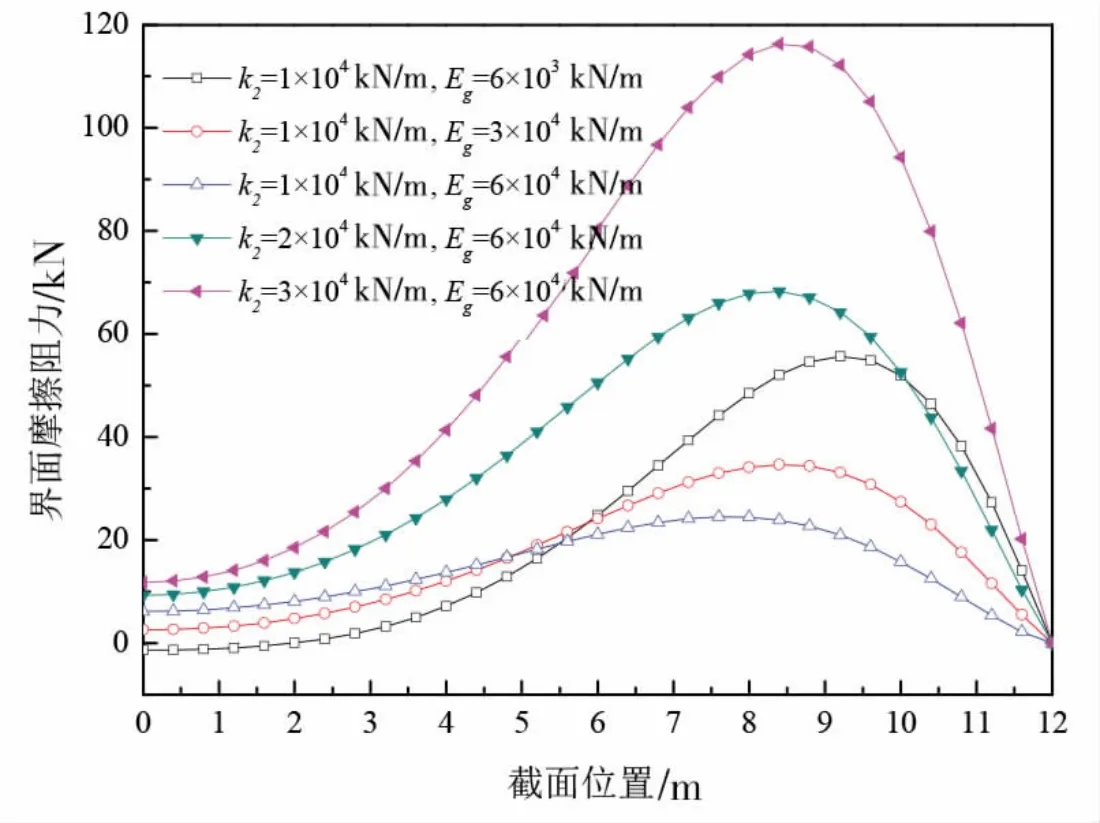
图6 不同筋材参数对界面摩擦阻力的影响Fig.6 Influences of different parameters of geosynthetic on interface friction
图7 为跨中作用1000 kN 竖向荷载时不同截面位置处筋材的拉应变。 当摩阻系数不变, 筋材拉伸模量增大为原本的5 倍与10 倍时, 其拉应变在正向与负向范围内皆明显减小, 跨中处筋材应变值分别减小了44.31%与61.42%, 表明增大拉伸模量可以防止其受拉破坏; 而当筋材的拉伸模量保持不变, 摩阻系数增大为原本的2 倍与3 倍时,筋材拉应变均有所增大, 跨中处筋材拉应变值分别增大了34.89%与53.09%。
3.2.2 基层参数的影响
图8 给出了加筋与不加筋时不同极限剪力的基层在荷载作用下路面的跨中挠度曲线。 比较加筋与不加筋两种情况, 当基层的极限剪力由10 kN增大至1000 kN, 跨中作用1000 kN 竖向荷载时挠度分别减小了7.07%与4.61%, 表明增加基层的极限剪力可以一定程度上减缓路面沉降。 同时, 基层中铺设筋材时路面的挠度会明显小于不加筋时拥有更大基层极限剪力的情况, 表明通过在基层中铺设土工合成材料, 可以有效地提升加筋路基的抗变形能力, 从而增强道路整体的稳定性。
3.2.3 水平荷载的影响
图9 给出了跨中作用1000 kN 竖向荷载以及不同大小水平荷载时, 路面结构的挠度变化曲线。从图中可以看出, 水平荷载的增大对梁端由一定影响, 其挠度变化有所增大, 路面向上翘起。 其原因是水平荷载与竖向荷载的耦合作用, 加剧路面结构翘曲。
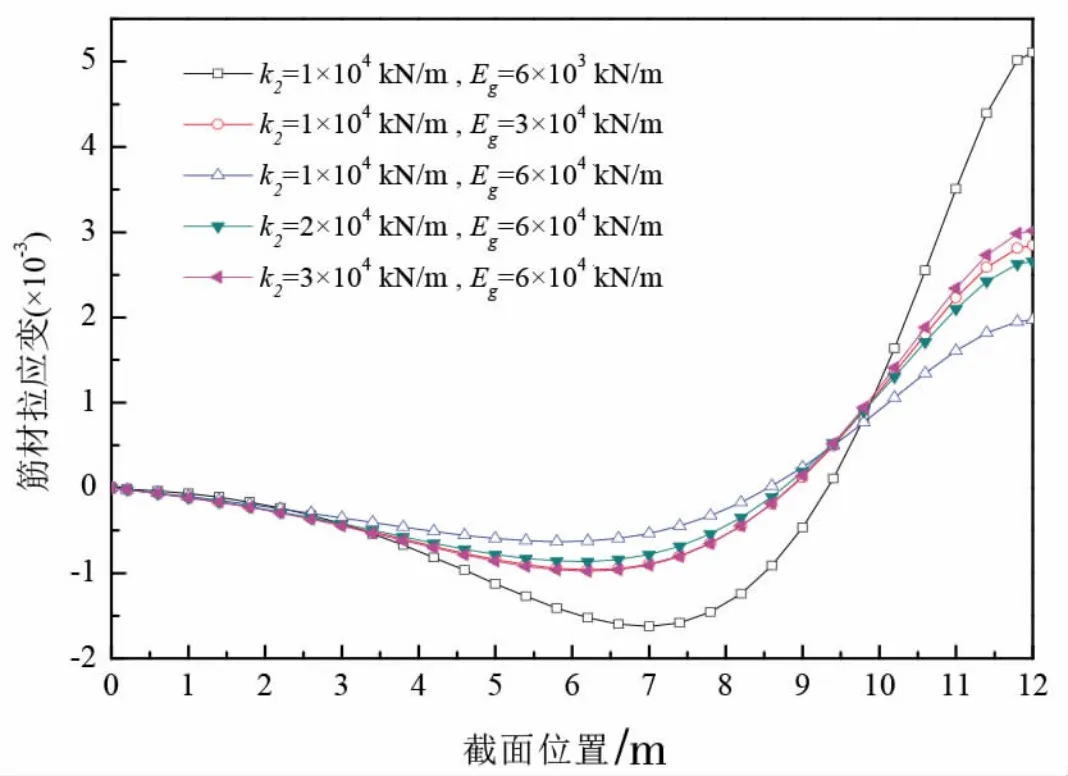
图7 不同筋材参数对筋材应变的影响Fig.7 Influences of different parameters of geosynthetic on strains
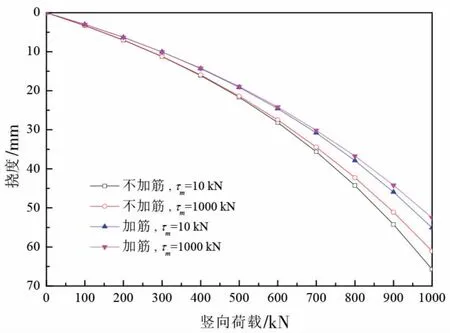
图8 不同基层参数对路面挠度的影响Fig.8 Influences of different parameters of subbase on deflections
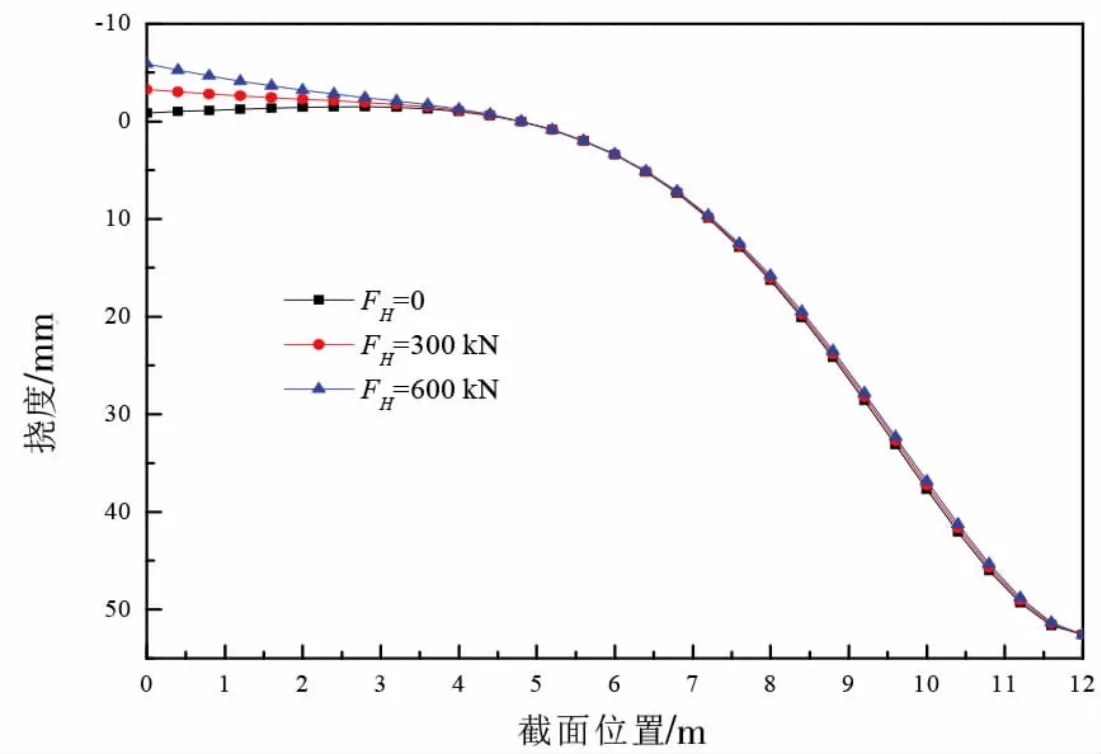
图9 水平荷载对路面挠度的影响Fig.9 Influences of horizontal loads on pavement deflections
图10 给出了跨中作用1000 kN 竖向荷载与不同大小水平荷载时, 筋材与上部基层间的摩擦阻力。 由图可以看出, 界面摩擦阻力随着距离梁端距离的增大先增大后减小; 而且随着水平荷载的增大, 界面整体的摩擦阻力有所增大, 当荷载增大至300 kN 与600 kN 时, 摩擦阻力极值分别增大了26.26%与52.49%, 且作用点的水平摩阻有所增大。 由此可见, 水平荷载的大小会明显地影响筋材与基层间的相对滑移和摩擦阻力, 所以通过铺设土工合成材料可以更好地减小水平荷载产生的影响, 提高结构抵抗变形的能力。
4 结论
(1)提升筋材与基层间的摩阻系数可以显著增强其加筋效果, 减小路面结构挠度, 增加界面摩擦阻力; 而采用抗拉模量较大的筋材可以减小自身的拉伸应变, 避免其受力破坏。
(2)对比加筋与不加筋两种情况, 在基层中铺设筋材可以有效地减小路面挠度; 同时, 随着基层的极限剪力的增大, 跨中挠度分别减小了7.07%与4.61%。
(3)路面处的水平荷载会明显地影响筋材与基层间的相对滑移以及摩擦阻力; 铺设土工合成材料可以减少制动荷载产生的影响, 提升抵抗变形的能力。
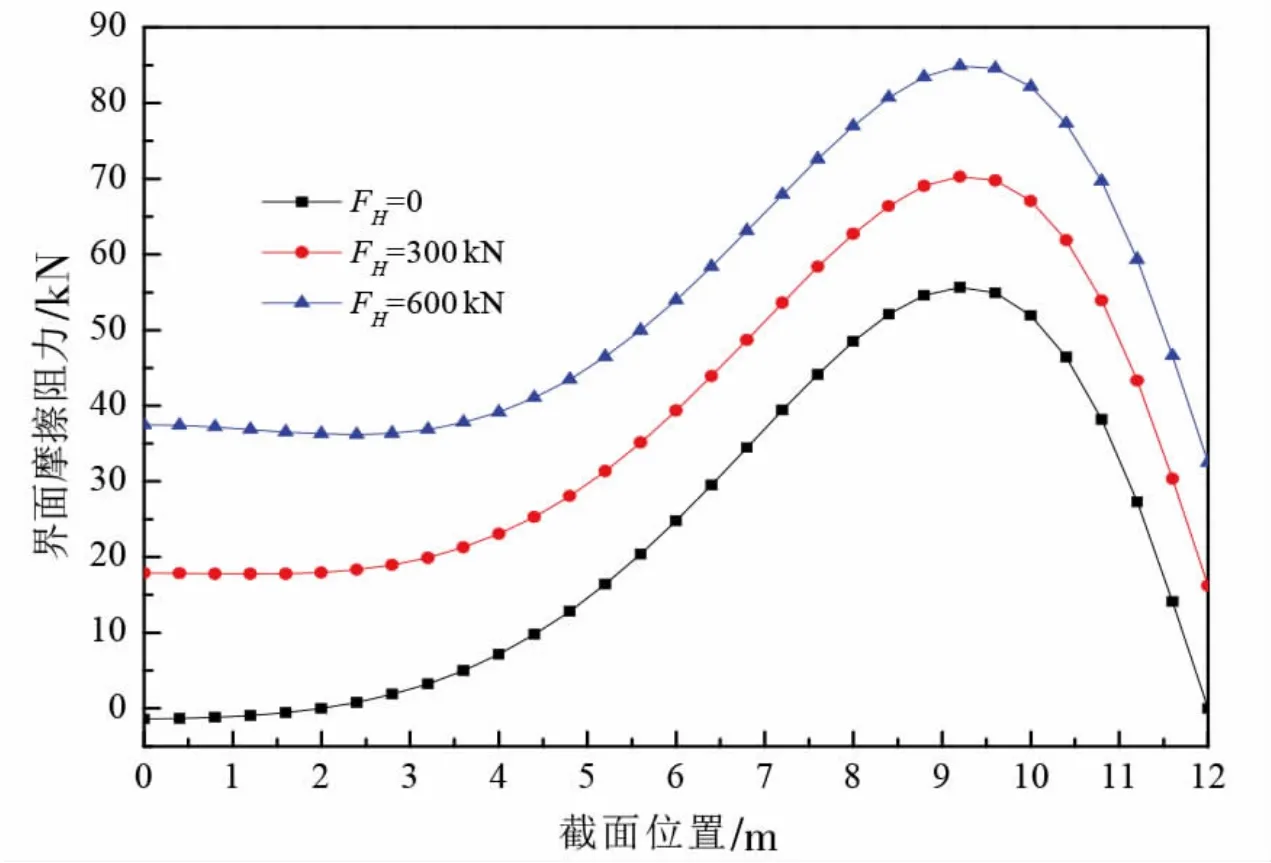
图10 不同水平荷载大小对界面摩擦阻力的影响Fig.10 Influences of different horizontal loads on interface frictions
