钢管混凝土构件承载力影响因素研究

谢开仲,梁亦登,王红伟,赵晓亮,魏 勇

(1.广西大学土木建筑工程学院,南宁 530004； 2.广西大学防灾减灾与工程安全重点实验室,南宁 530004)

引言

钢管混凝土结构是指在钢管内填充混凝土使其约束核心混凝土共同承受外界荷载的组合构件，因为兼具钢材和混凝土两种材料的力学性能优点，服役过程中可以充分发挥两者的材料性能，被广泛应用于拱桥拱肋、设备支柱、桁架压杆、地下结构、住宅厂房及高层建筑等结构[1-3]。

在钢管混凝土柱中，益于钢管的约束作用，核心混凝土不会过早地发生破坏，同时核心混凝土的支撑作用也避免了钢管发生局部屈曲，钢管和混凝土的相互作用使组合构件的力学性能发挥到了极致，构件即使在破坏时也能表现出较好的塑性变形能力，因此具有广阔的工程应用市场。目前，国内外学者也对钢管混凝土构件进行了诸多研究工作，并取得了丰富的研究成果：柯晓军[4]等通过40组钢管混凝土试验，提出能够考虑钢管及其约束作用的正截面压弯承载力计算公式；赵国飞[5]等对于不同龄期钢管混凝土短柱，引进龄期套箍修正系数，建立了早龄期钢管混凝土短柱的承载力计算公式；周理[6]等基于拉杆-拱模型提出方钢管混凝土轴压承载力计算公式；杨绿峰[7]等基于构件承载能力极限状态并合理考虑受拉区钢管的应变强化段，提出方钢管混凝土受弯构件的承载力失效判据。目前关于钢管混凝土柱的极限承载力还没有统一的计算方式，各学者也在不断探索精准简化的计算公式，并逐渐延伸到异形截面柱方面。颜燕详[8]等提出异形钢管混凝土柱偏压承载力统一算法，但仅限于T形、L形和十字形钢管混凝土柱；徐礼华[9]等建立多腔式钢管混凝土柱偏心受压承载力计算公式，但是验证截面形式较少；Hassanein[10]等提出了高强混凝土椭圆钢管混凝土柱承载力设计公式。在钢管混凝土柱力学性能探索上，也对不少相关参数进行了定性分析。龚永智[11]等结合试验和三维实体非线性有限元模型分析配置圆环箍筋和螺旋箍筋对方钢管混凝土柱受力性能的影响；余敏[12]等研究了钢管混凝土的多级加载与核心混凝土收缩徐变的耦合作用；廖飞宇[13]等通过12根短柱的滞回性能试验，研究环向脱空初始缺陷对钢管混凝土在压弯扭共同受力作用下的抗震性能；刘明辉等[14]研究了界面缺陷范围对混凝土的损伤影响和钢管混凝土构件抗弯刚度的折减规律。同时在钢管混凝土的抗火性能方面也有一定的研究。C. Ibaez等[15]建立了钢管混凝土柱后热响应的纤维模型，分析了加热、冷却和火灾后(在持续荷载下)条件下钢管混凝土柱的受力特征；V. Albero等[16]对5046个案例进行了广泛的参数研究，提出新的钢管混凝土柱简化火灾承载力设计方法；项凯[17]等研究8根短柱的受火冷却后轴压承载力试验，发现短柱受火冷却后轴压极限承载力降低30%左右。然而当前对钢管混凝土压弯破坏方面报道较少，对截面偏心率的定量分析也仍有不足。

钢管混凝土拱桥的拱肋病害有多种[18]，压弯破坏是其破坏模式之一，本文据此探索钢管混凝土柱的受力性能及破坏模式，开展9个试件的轴压及偏压试验，结合建立的ANSYS精确合理的数值模型，揭示钢管混凝土组合构件的受力机理及纵向、环向应力应变发展规律，进一步分析偏心率、长径比、材料等级和径厚比等试验因子对构件极限承载力学性能的影响规律，以期为实际工程提供理论参考依据。

1 试验概况

1.1 钢管混凝土试件参数设计

为研究材料等级、偏心率、长径比等试验因子对钢管混凝土力学性能的影响，本试验进行9个钢管混凝土试件的轴压及偏压力学性能研究，各试件详细参数如表1所示。

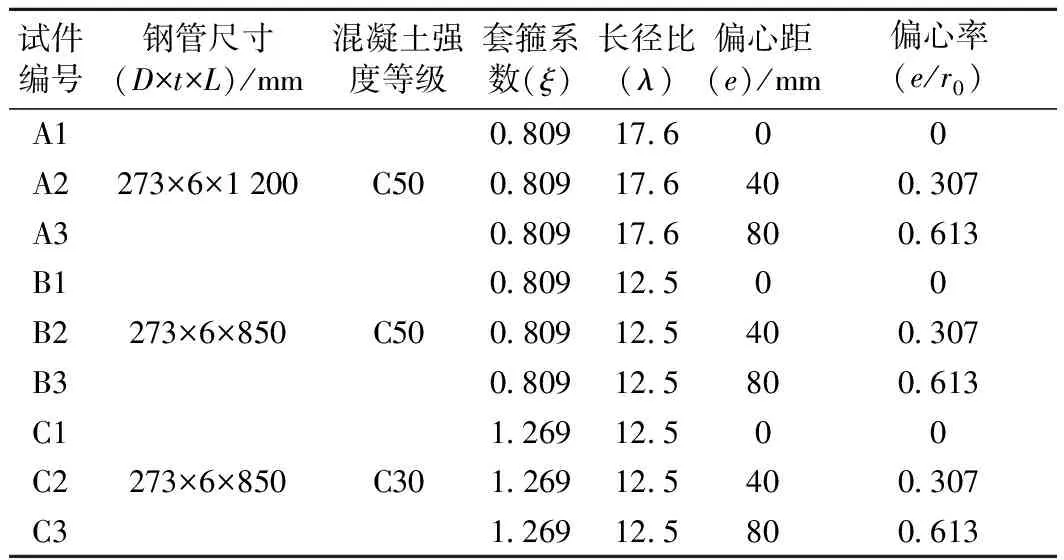
表1 试件编号及主要参数

1.2 试验加载及数据采集

本次试验使用的加载装置为YAW-10000J微机控制电液伺服压力试验机，具有4 000 kN压力传感器测量系统和静态应变测量系统。试验加载装置示意见图1。

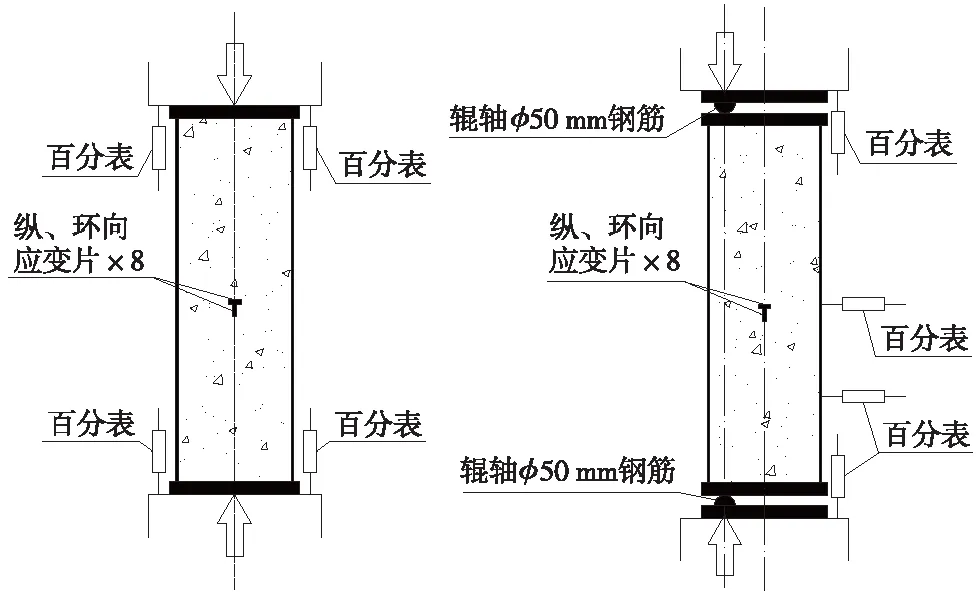
图1 轴心受压和偏心受压试验装置示意

钢管混凝土轴心受压试件通过上下盖板施加轴向压力，偏心受压试件通过盖板上的锟轴对其施加偏心压力，加载方式均采用分级位移加载，试件在弹性阶段加载速度为0.5 mm/min，非弹性阶段加载速度为0.2 mm/min。每个试件的中间均布置有20个电阻应变片，其中12个应变片贴于核心混凝土上用以测试其纵向应变，在钢管外壁4个方位对称布置纵、环向应变片，分别测试钢管的纵向应变和环向应变。为测定轴压试件在各级荷载下的总压缩量，在盖板处对称布置2个百分表测量试件受压过程中的纵向位移，并通过压力试验机的位移传感器进行实时校对。偏压试件在沿柱高四分点位置和中间位置安装了百分表，用来测试偏压试件的侧向变形。

1.3 试验现象及破坏形态

图2为试验中9个试件的受压破坏状态，轴压试件在材料弹性阶段无明显变化，在达到荷载峰值的80%左右时，钢管外壁开始出现交叉斜裂纹，随着荷载继续增大，在有初始缺陷处将首先发生屈曲。试件破坏时两端和中部有明显鼓曲现象，并产生斜向剪切滑移。

图2 试验破坏后的试件

偏心受压试件在加载初期变形微小，当竖向力达到峰值荷载时，应变和挠度变化加快，试件中部产生明显挠曲变形。随后荷载进入下降或者平缓段，构件两端受压区钢管均已屈服，并有向外明显鼓曲现象，进入破坏阶段时，试件明显弯曲且有细微裂缝，大部分应变片溢出。

1.4 试验结果分析

1.4.1 荷载-纵向应变曲线

轴压构件在荷载不断增大的持续作用下，其薄壁钢管最终会无法抵抗混凝土膨胀而发生剪切破坏，而偏心加载构件主要发生压弯破坏，混凝土钢管的纵向应变发展可以反映出构件的主要力学性能。图3给出了各试件的荷载-纵向应变关系曲线。

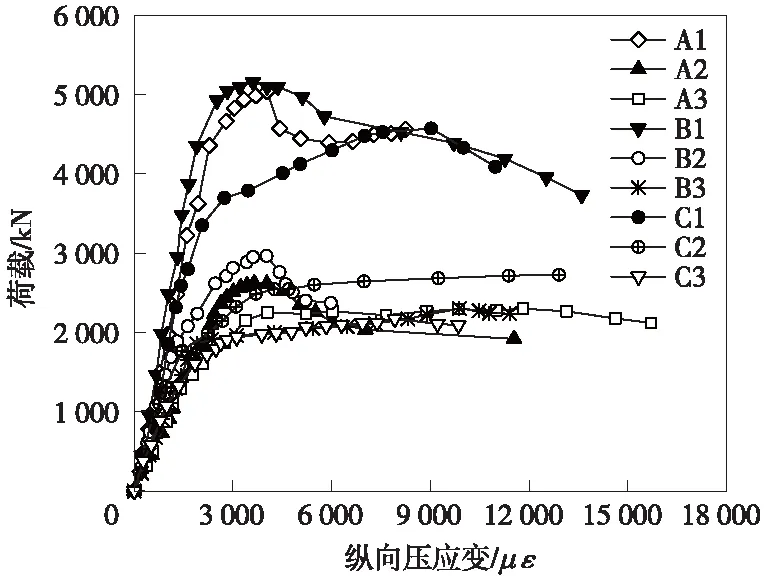
图3 各试件的荷载-纵向应变曲线

受荷初期，试件的纵向应变随荷载呈直线增加，即线弹性增长阶段；当荷载达到极限荷载的70%～80%时，荷载-应变曲线进入屈服阶段，纵向应变呈曲线增加，此时应变值为2 000 με左右，已大于钢管的单轴抗拉屈服应变1 578 με，表明此时钢管纵向应力已进入弹塑性阶段，钢管和混凝土之间发生应力重分布，应变继续有小幅度的增长，最后达到破坏状态。

对于A组(ξ=0.957)和B组(ξ=0.957)试件，荷载达到峰值后，荷载-应变曲线开始出现下降趋势，而C组(ξ=0.1.269)试件曲线则以较低斜率继续保持增长，说明随着套箍系数的增大，钢管对核心混凝土的套箍作用愈发明显。

1.4.2 荷载-环向应变曲线

钢管对核心混凝土的约束作用使钢管混凝土柱的应力分布更具复杂性，因此通过分析钢管壁的环向应变来研究套箍机理是有必要的。图4和图5给出了各构件从加载初期到峰值荷载时的荷载-环向应变关系曲线(1H表示受压一侧测点，3H表示受拉一侧测点；应变值单位拉为正，压为负)。

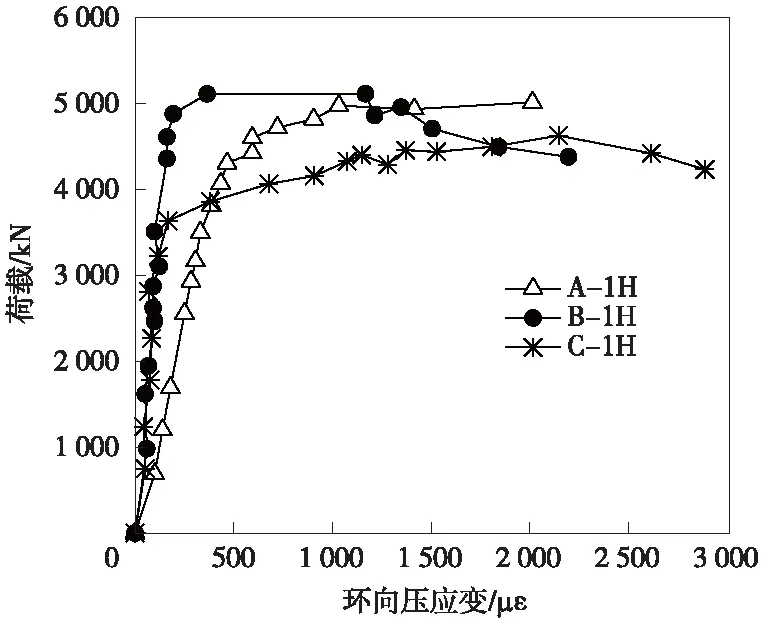
图4 轴压试件荷载-环向应变曲线

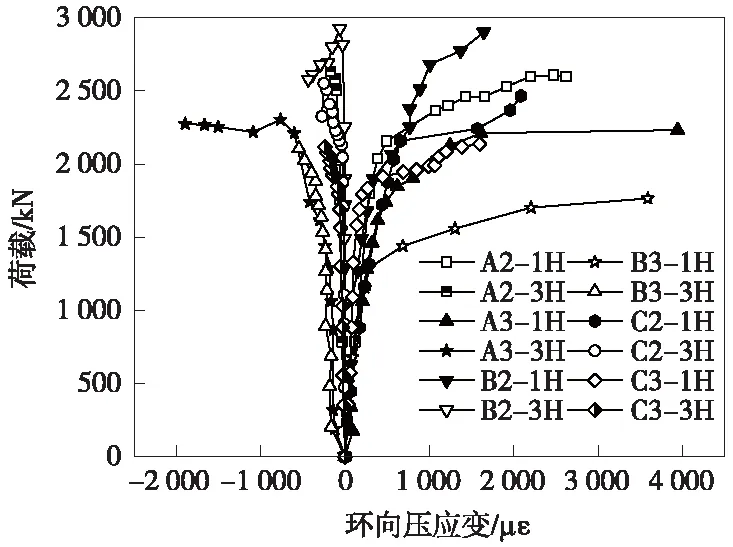
图5 偏压试件荷载-环向应变曲线

在轴压试件中，4个方向的传感器显示的环向应变曲线基本重合，因此只取1H测点进行分析比较。由图4可以看出，所有的轴压试件环向应变始终处于受拉状态，在加载初期，试件的环向应变较小且呈线性增长，表明此时钢管对核心混凝土未产生约束作用。当荷载达到峰值荷载的80%左右时，荷载-环向应变曲线不再呈线性增长，环向应变表现为急剧增加，说明钢管纵向屈曲开始卸载，此时钢管的环向应变约为屈服应变的20%。当峰值荷载达到时，所有轴压试件钢管的环向应变均已接近或超出屈服应变1 578 με，钢管4个方向测点区域均表现良好的约束作用。

与轴压试件不同，偏心受压试件中的受压加载侧区域3H测点表现为受压，其余三个环向应变测点表现为受拉状态，取3H测点和其相对的1H测点分析比较。对于小偏心受压试件(A2、B2、C2)，在加载初期，受压较小区域1H测点的变化不明显，几乎为0，后期荷载峰值有较大变化，这表明加载初期钢管整体表现为纵向受压，远离偏心一侧钢管由环向受压转为环向受拉，甚至并未受到核心混凝土挤压作用；对于大偏心受压试件(A3、B3、C3)，加载初期1H和3H测点便表现明显的压应变和拉应变。两组试件当达到极限承载力时，偏心侧1H环向拉应变均已超出1 578 με，而远离偏心力侧3H测点还未达到屈服点，仍处于弹性受压阶段。这说明在偏心受压试件中，偏心一侧区域钢管主要起到了约束核心混凝土的作用，其余区域钢管发挥的约束效应较小。

2 数值模型建立

为探索各试验因子对钢管混凝土柱力学性能的影响规律，本文将在试验的基础上，结合ANSYS数值模型，弥补试验不足之处，进一步研究钢管混凝土受力机理。

2.1 模型材料的模拟

构件钢管选用ANSYS中的shell181号单元建模，采用双线性各向同性弹塑性材料来模拟钢材的应力应变关系，其屈服强度采用钢管材料力学性能试验所得的强度值325 MPa。它应用的是Von-Mises屈服条件，其应力应变关系如下

(1)

核心混凝土本构关系采用韩林海[19]提出的纵向应力-应变模型，充分考虑了钢管约束效应和混凝土强度的影响，其表达式如下。

当εc≤ε0时

σc=σ0[A(εc/ε0)-B(εc/ε0)2]

(2)

当εc>ε0，ξ≥1.12时

σc=σ0(1-q)+σ0q(εc/ε0)0.1ξ

(3)

当εc>ε0，ξ<1.12时

σc=σ0(εc/ε0)/[β(εc/ε0-1)2+εc/ε0]

(4)

式中

2.2 边界条件及加载方案

边界条件：为了使钢管和混凝土共同受力以及更符合实际试验情况，在模型两端分别设置刚性垫板；对于偏压构件，在垫板上设置钢条模拟辊轴用以偏心加载。

荷载的施加：和实际试验一样，采用位移加载方式以得到更为精准的应力-应变曲线。对于轴压试件，只要将试件上部刚性垫板节点施加位移荷载。对于偏压试件，则将条形钢节点施加荷载，这样便等效于将荷载均匀作用于构件。有限元计算模型如图6所示。

图6 钢管混凝土有限元模型

2.3 有限元分析与试验结果的对比

为验证有限元计算结果的准确性，表2列出了所有试件有限元计算与试验实测的极限承载力及其相对误差。

表2 极限承载力实测值与计算值比较

由表2可知，有限元计算值与实测值总体上相差不大，除个别构件外(构件的初始缺陷导致其承载力偏小)，其余构件的承载力实测值与有限元计算值相对误差值均不超过7.6%，其误差在工程允许范围内，说明本文建立的有限元模型可以应用于钢管混凝土力学性能的进一步研究。

3 承载力影响因素分析

本章将利用验证后的数值模型进一步分析偏心距、混凝土强度、长径比和径厚比等试验因子对钢管混凝土力学性能的影响。以B1试件为标准试件，改变各试验因子参数，分析各试验因子对钢管混凝土极限承载力的影响规律。目的是为了对试验结果进行补充，以期得到一些更加具有普遍意义的结论，并为实际工程参考依据。

3.1 偏心距的影响

偏心距对构件极限承载力的影响结果如图7所示。可以看出，随着偏心率的增大，钢管混凝土短柱的承载力出现明显下降趋势，偏心率为0.3时，极限承载力已减少了33.7%。在小偏心受压阶段(e/r0≤0.3)，短柱的极限承载力下降的较为明显；在0.3≤e/r0≤0.6阶段，偏心率-极限承载力曲线开始趋于缓和，说明钢管对核心混凝土的套箍作用开始增强：在偏心率e/r0≥0.6阶段，短柱的极限承载力又呈线性下降趋势，构件出现大偏压破环。

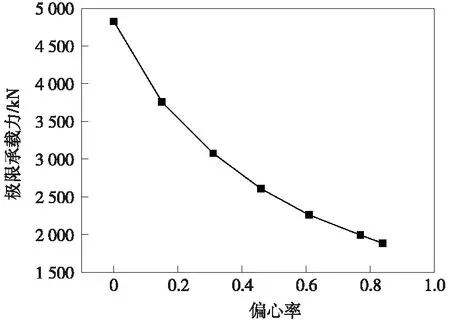
图7 偏心率-钢管混凝土极限承载力

3.2 材料等级的影响

混凝土材料等级对构件极限承载力的影响结果见图8。可以看出，随着混凝土强度的提高，钢管混凝土构件的极限承载力也随之提高，当核心混凝土采用C30混凝土时，构件极限承载力为3 526 kN，采用C80高强混凝土时，极限承载力达到了5 844 kN，提高了65.7%。承载力-强度曲线几乎呈线性增长趋势，这是因为轴压短柱构件主要发生材料破坏[20]，在持续增大荷载作用下，其外包薄壁钢管首先发生屈服，应力重分配过程中，核心混凝土强度愈高，所能承担的荷载就愈多，直至混凝土溃散，构件达到极限承载力状态。

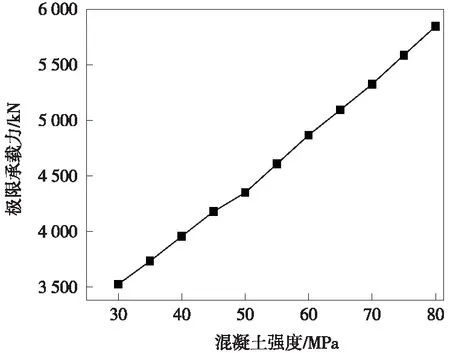
图8 混凝土强度-钢管混凝土极限承载力

3.3 长径比的影响

设计2组试件，一是假设构件为理想试件，即不考虑构件的初始缺陷，以探索钢管混凝土短柱和长柱的长径比界限；二是为使构件更贴合实际，考虑构件初始缺陷为初偏心(幅值为L/1 000)，分析长径比对构件承载力影响。计算结果如图9所示。

图9 长径比-钢管混凝土极限承载力

可以看出，理想构件的极限承载力随着长径比增加而降低，当长径比达到18后，极限承载力几乎不再发生变化，说明短柱和长柱的长径比界限为18；考虑初偏心L/1 000的初始缺陷构件的极限承载力随着长径比增大而不断减小，但是减小幅度不大，其破坏模式也从受压破坏转为压弯破坏，长径比达到60后曲线趋于缓和，而长径比达到90后，构件极限承载力开始骤降，建议实际工程中钢管混凝土柱不宜过长，长径比最好不要超过90。

3.4 径厚比

径厚比大小对构件极限承载力的影响结果如图10所示。可以看出，构件的极限承载力随着径厚比的增大而减少，承载力-径厚比曲线呈现为经典反比例函数曲线。当短柱径厚比从20变化到40时，构件的极限承载力减少21%：当长径比从40变化到100时，构件的极限承载力也仅减少21%左右。这是因为径厚比增大，外壁钢管相应减薄，故而钢管承担荷载比例减少，加速了构件屈曲的发生，同时对核心混凝土的约束效应也相应减弱。

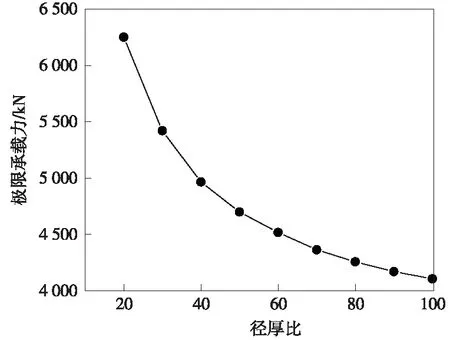
图10 径厚比-钢管混凝土极限承载力

4 结语

(1)从钢管混凝土构件的轴压及偏压试验的破坏形态及应力应变对比曲线可以看出，偏心率对钢管混凝土极限承载力的影响是显著的：当偏心率为0.3时，构件承载力折减可达30%～40%；当偏心率为0.6时，其承载力折减可达50%～60%。建议实际工程中应采取措施避免或减小构件承受偏心力作用。

(2)通过对钢管混凝土构件不同偏心率加载的试验及数值分析，发现钢管对核心混凝土产生约束效应区域是有限的，且与偏心率大小有关，当轴压时，钢管四周外壁对混凝土均有明显的约束作用，而偏压时，只有偏心加载一侧钢管对混凝土有较大约束，其他侧面钢管还未达到屈服状态，发挥的约束效应十分有限。

(3)本文研究的混凝土强度、长径比和径厚比等试验因子对钢管混凝土力学性能均有较大影响。随着核心混凝土强度的增加，构件的极限承载力呈线性增长，实际工程中可采用高强混凝土以提高组合构件的承载能力；构件极限承载能力随径厚比增大而减弱，当短柱径厚比从20变化到40时，构件的极限承载力减少了21%左右，当径厚比从40变化到100时，构件的极限承载力也仅减少了21%；短柱和长柱的长径比界限为18，当长径比小于18时，构件主要发生剪切破坏，当长径比大于18时，构件主要发生压弯破坏，极限承载力不断减小。