基于平均值等效的IGCT-MMC损耗特性分析与计算

2021-04-23郭明珠白睿航唐博进赵彪周兴达余占清曾嵘

南方电网技术 2021年3期

郭明珠，白睿航，唐博进，赵彪，周兴达，余占清，曾嵘

(1.中国长江三峡集团有限公司科学技术研究院，北京100038；2. 电力系统及发电设备控制和仿真国家重点实验室(清华大学)，北京100084)

0 引言

可再生能源利用是未来能源领域发展的大势所趋。有预测指出，到2050年，中国可再生能源将占能源消费50%以上[1]。高压直流电压源型换流器(high voltage direct current voltage source converter，HVDC-VSC)以其调节灵活、谐波低、效率高等优点，被广泛用于可再生能源并网[2 - 3]。模块化多电平换流器(modular multilevel converter, MMC)是HVDC-VSC技术的常用拓扑结构之一[4 - 5]。目前，绝缘栅双极型晶体管(insulated gate bipolar transistor，IGBT)以其高耐压、高通流、高开关频率、较低的开关损耗以及尚可接受的通态损耗等优势，在MMC中得到广泛应用[6 - 7]。

集成门极换流晶闸管(integrated gate-commutated thyristor，IGCT)是从门极可关断晶闸管(gate turn-off Thyristor，GTO)发展而来的大功率全控型电力电子器件，由ABB公司于1996年首先成功研制[8 - 9]。相比于IGBT，IGCT器件具有流控器件的优势，例如通流能力更强、阻断电压更高、通态压降更低，且存在进一步发展潜力[10]。

MMC采用模块化设计，依靠高模块数量而非高调制频率实现低谐波的电压输出，这规避了IGCT开关频率低的不足，为IGCT应用于柔性直流输电领域带来了契机。MMC的低开关频率特性导致其运行时，器件的通态损耗占比相对更高，使用IGCT代替IGBT则有助于减小该部分损耗。目前，商品化的IGCT阻断电压已达6.5 kV，而IGBT仅为5.2 kV，基于IGCT器件的MMC有可能提高单模块电压等级，从而减少模块数量，降低占地面积。此外，IGCT以其高浪涌电流耐受能力，还为半桥MMC的故障穿越提供了新的可能方案[11 - 12]。

文献[13]对IGCT在柔性直流输电领域的应用进行了展望。文献[14]对IGCT-MMC半桥子模块拓扑、电路特性等进行了分析，搭建仿真模型进行损耗分析，并搭建了对冲平台进行实验。文献[15]同样通过搭建仿真模型的方式分析了IGCT-MMC的损耗。事实上，由于MMC子模块数量巨大，通过仿真分析损耗运算量大，较为繁琐。文献[16]提出了一种通过平均值等效的方式计算子模块各器件电流并分析损耗的方法，据此分析了基于IGBT的MMC器件损耗与结温，并通过实验进行了验证。

针对以上研究现状，本文基于平均值等效的方法，分析了IGCT-MMC中的IGCT器件、缓冲电路、取能电源等各部分损耗的计算原理，给出了计算方法。结合具体工程参数，通过MATLAB编程给出了算例，并与模拟实际投切过程进行仿真计算的结果进行了对比。

1 基于平均值等效的IGCT-MMC损耗分析方法

1.1 基于IGCT的MMC子模块

IGCT与IGBT同为全控型功率半导体器件，IGCT-MMC子模块和IGBT-MMC子模块在主电路拓扑上相同。IGBT为压控器件，可通过控制其栅极触发信号上升陡度来控制开通速率。而IGCT的开通过程类似于晶闸管，为正反馈过程，无法通过门极驱动电路控制其开通速率，因此，IGCT开通时，功率半导体器件中会产生很大的di/dt。

尽管当前快恢复二极管和新型IGCT器件有较好的di/dt耐受能力，但过高的di/dt仍会导致其损坏，因而需要在换流回路中串入阳极电抗以限制电流变化速率[17 - 18]。阳极电抗会导致投切瞬态过程中产生振荡，这可能引起器件过压击穿，故还需设置箝位电路以保护器件。阳极电抗与箝位电路统称缓冲电路。一种设置了缓冲电路的IGCT-MMC子模块拓扑如图1所示。

此外，IGCT通态中需要持续向门极注入电流，关断时需要从门极抽出上千安培的电流，这使得其门极驱动功率可达数十瓦甚至上百瓦，大于IGBT的驱动功率。

由于评估IGCT-MMC子模块损耗时，需要考虑缓冲电路与门极驱动损耗，因而其分析与计算过程更加复杂。

1.2 平均值等效模型

子模块电流方向、投切状态不同时，桥臂电流会流经不同功率半导体器件，因而各半导体器件损耗存在差异。为计算损耗，需要分析流经各器件的电流。桥臂电流方向决定了电流流经的功率器件对(T2/D2或T2/D1)，投切状态又进一步确定了通流器件。具体情况如表1所示。选取电流流入子模块为桥臂电流参考方向。

表1 不同状态下电流流经的功率器件Tab.1 Power devices with current passed in different states

以下桥臂为例(上桥臂类同)，定义瞬时调制比k为当前该桥臂中投入模块的数量在桥臂总模块数中占比，可根据参考电压算出。

(1)

式中：uacφ(t)为系统级控制在t时刻需要某一桥臂输出的电压值；udc(t)为此时该桥臂所有子模块电容电压之和。

在平均值等效模型中，认为一个桥臂中，每一时刻下，所有子模块被投入或切除的机会均等。在该前提下，任一时刻，各子模块电流并非按照表3的规律全部流经一个器件，而是“同时”流经电流方向所决定的一对功率器件。电流在两个功率器件间的分配由投切概率决定。若桥臂电流为iarm，定义sgn(x)为符号函数，当x>0时为1，否则为0，abs(x)为绝对值函数，则平均值等效意义下，通流期间流经器件对T1/D2的电流iT1-D2、流经器件T1的平均电流IT1mean与均方根电流IT1rms可由下式计算。

iT1-D2=abs{sgn[-iarm(t)]×iarm}

(2)

iT1(t)=k(t)iT1-D2(t)

(3)

(4)

(5)

式(4)—(5)中，ti<0为1个基波周期内桥臂电流小于0，也即电流流经器件对T1/D2的时间段。使用该方法还可以得到流经其他功率器件的电流。同理，也可得到全周期内流经阳极电抗的电流均方根值ILrms。

(6)

平均值等效模型还忽略了子模块电容电压波动。由于工程中通常要求子模块电容电压波动不超过10%，且子模块电容电压并非存在固定偏置，而是随着电容充放电在额定电压附近波动，因此，这样的简化不会给分析带来过大误差。

由于高压大容量MMC中的模块数通常有数百个，模拟各子模块投切过程，进而通过器件实际电流波形仿真计算其损耗的方法所需计算量大，特别是需要频繁优化电路参数并估算子模块损耗时，所需的计算时间长。平均值等效模型只需要对单子模块进行计算，即可得到各个器件的损耗功率，适合于在换流器设计与优化阶段用以评估损耗。此外，平均值等效模型可以给出平均值意义下流经器件的电流波形，从而直观看出器件损耗差异的原因。

2 IGCT器件损耗分析

2.1 通态损耗

与IGBT器件通态损耗分析类似，导通的IGCT器件上存在压降，这一压降与IGCT通流为非线性关系，可以通过线性关系进行拟合，即将器件导通压降vX1分为门槛电压vX0，以及斜率电阻rX乘以通流iX两部分，其中X代表任一IGCT器件。

vX1=vX0+rXiX

(7)

进而可得到器件通态损耗功率计算公式为：

(8)

第一部分可等效为电流向一个恒压源充电，第二部分可看作电流流经固定阻值的电阻。以T1为例，可以用其平均电流代替上式电流一次项，用均方根电流代替电流二次项，进而得到通流时间ti<0内IGCT通态损耗平均功率为：

(9)

在整个工作周期T内，器件T1的通态损耗平均功率为：

(10)

2.2 开关损耗

IGCT开关瞬态过程非理想过程，存在电压、电流重合的时间区段，这会引起开关损耗。开关损耗包括IGCT开通损耗、IGCT关断损耗和二极管反向恢复损耗。通常，器件数据手册中给出了特定电压、电流下的开关损耗数据，在分析时需要将其折算至实际工况下的具体值Eb。

(11)

式中：下标b代表IGCT开通、关断、二极管反向恢复等行为；EbN为电压VN；电流IN下行为b的损耗能量，由数据手册给出；vb为开通前/关断后器件电压；ib为开关行为发生时开通/关断的电流大小。若器件在固定电压、电流下以固定频率f开关，则其开通、关断损耗功率Pb为：

(12)

对于MMC子模块而言，vb为子模块额定电压VSM。在平均值等效模型下，以电流负向、将投入的子模块切除为例，这一过程会关断T1，电流转移至D2。由于投切时刻随机，T1关断电流大小可以看作对于流经T1-D2器件对电流的一次随机采样。从统计意义而言，T1关断电流的大小即为T1-D2器件对通流时间内的平均电流。仅当电流为负向时，子模块切除动作会导致T1关断，因而T1的关断频率为：

(13)

进而有：

(14)

3 缓冲电路损耗分析

3.1 阳极电抗直阻损耗

由于阳极电抗具有直流电阻，MMC运行时，流经阳极电抗的电流会因焦耳效应产生损耗PL，其计算公式为：

(15)

式中：RL为阳极电抗直流电阻。可以代入第1.2节的阳极电抗电流均方根值进行计算，则：

PL=ILrms2RL

(16)

3.2 箝位电路动作损耗

箝位电路仅在子模块投切的瞬态过程中动作，箝位电阻焦耳效应、箝位二极管反向恢复均会导致能量损耗。文献[19]指出箝位电路单次动作时，阳极电抗能量的70%耗散于箝位电路。则单次动作时箝位电路能量损耗Wcl为：

(17)

式中：La为阳极电抗感值；IL为子模块投切时刻其阳极电抗的电流。

根据文献[9]的分析，每次投切瞬态过程均会引起箝位电路动作。因而箝位电路动作频率为子模块投切频率的2倍。平均值等效模型中，箝位电路单次动作时阳极电抗的电流变化是对子模块电流的随机采样，且单次损耗中电流为二次项，则箝位电路损耗Pcl可以由式(18)计算。

(18)

4 取能电源损耗分析

取能电源消耗的功率取决于其输出功率。在IGCT-MMC子模块中，驱动电源输出功率大部分用于IGCT门极驱动。因此，需要准确评估MMC工况中IGCT的门极驱动功率。

4.1 IGCT门极驱动原理与功耗分析

IGCT门极驱动主要包括开通模块、关断模块，以及控保与供电等辅助电路。为确保IGCT可靠、迅速开通，开通时需要向门极注入脉冲电流。导通状态下，为避免电流过零点时自然关断，还需要注入稳定的维持电流。关断过程中，关断模块在门阴极间施加反压，从而将阴极的工作电流抽出至门极，完成关断。IGCT门极驱动原理示意如图2所示。

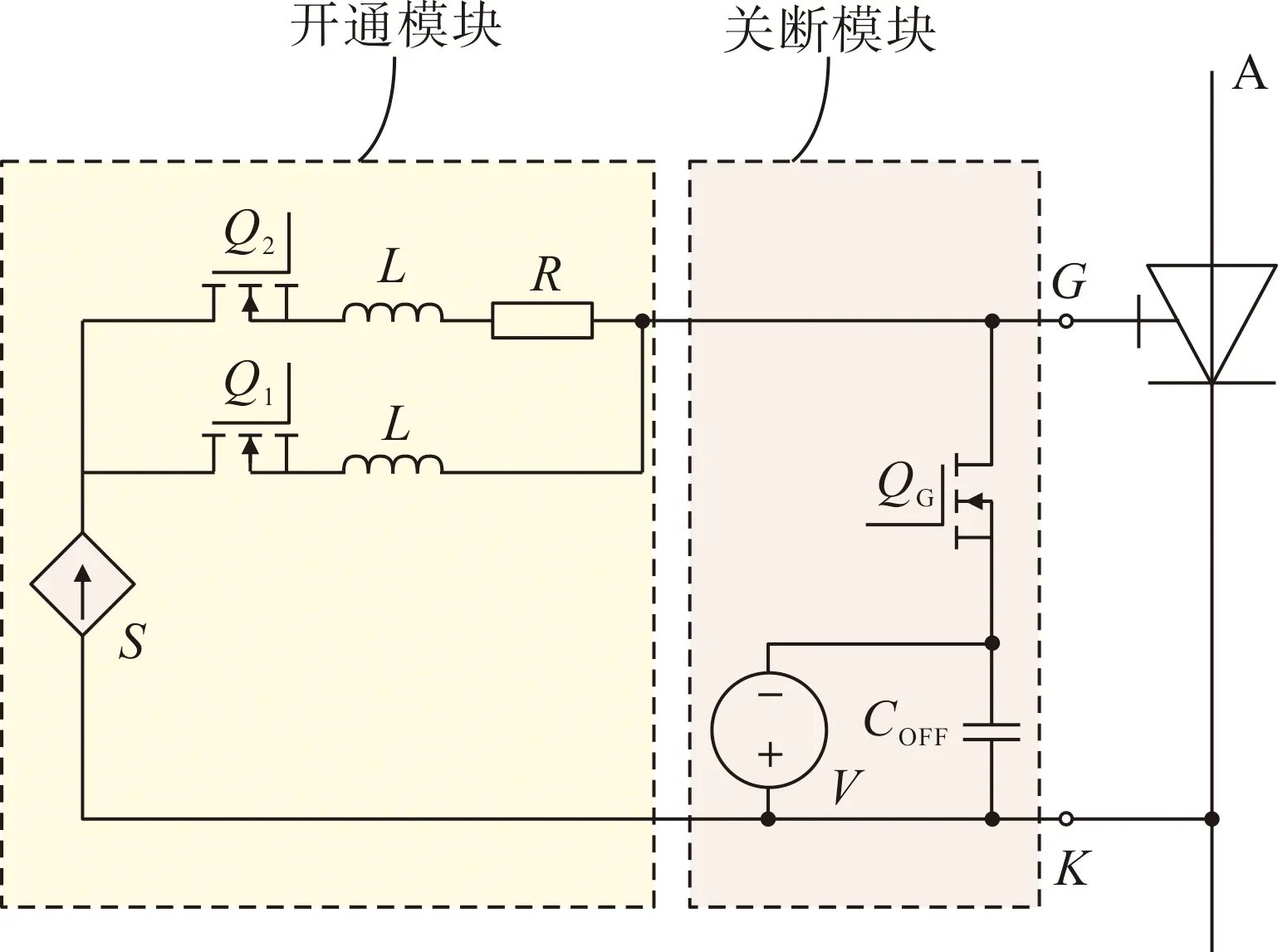
图2 IGCT门极驱动原理示意Fig.2 Principle of IGCT gate drive

根据原理分析，IGCT门极驱动功耗主要由以下5部分组成。

1)静态功耗，即控制、检测、保护等电路功耗，相对固定；

2)开通行为中，向门极注入脉冲电流的功耗，与开关频率正相关；

3)导通状态下，向门极注入稳态电流的功耗，与占空比正相关；

4)关断行为中，电容抽取门极电流产生的功耗，与开关频率、关断电流正相关；

5)开通电容充电电路、关断电容充电电路、输入稳压电路等产生的损耗，与以上4项均有关。

因此在忽略占空比因素的情况下，IGCT器件门极驱动功率与关断电流、开关频率均呈线性关系。

4.2 恒定电流下门极驱动功率计算公式

子模块选用国内某半导体公司生产的，具有失电阻断能力与高浪涌耐受能力的IGCT-Plus器件。该器件数据手册中给出不同开关频率下，门极驱动功率-关断电流图如图3所示。

图3 IGCT门极驱动功率-关断电流Fig.3 Power of IGCT gate drive-turn-off current

从图3可以看出，频率给定时，IGCT器件门极驱动功率与关断电流近似为线性关系。根据图中数据，还可以作出关断电流给定时的门极驱动功率PG与开关频率f关系如图4所示。

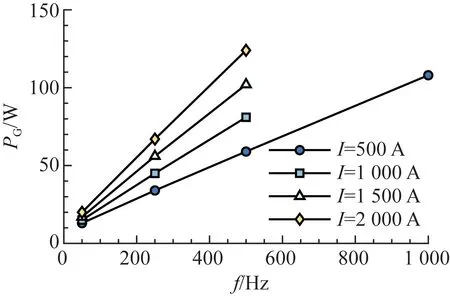
图4 IGCT门极驱动功率-开关频率Fig.4 Power of IGCT gate drive-switching frequency

可见，在固定关断电流下，门极驱动功率与开关频率也为线性关系，这与理论分析相符。恒定通流下，IGCT门极驱动功率PG与关断电流Ioff、开关频率f在空间直角坐标系中所形成的曲面为直纹面，其解析式为：

PG=k1+k2f+k3Ioff+k4fIoff

(19)

为提高拟合精度，取相距较远的4个数据点代入公式，求解线性方程组，即可得到4个常数值。最终拟合得到的门极驱动功率计算公式为：

PG=7.51+0.063 3f-0.005Ioff+0.086 7fIoff

(20)

式中：f单位为Hz；Ioff单位为kA；PG单位为W。

4.3 MMC工况中取能电源功率计算方法

根据第2.2节的分析，可以将IGCT对应器件对的平均电流作为关断电流，以及式(13)所确定的IGCT开关频率代入式(20)，进而计算该器件门极驱动功率。

将两个IGCT门极驱动功率相加，并考虑控制板卡功率、取能电源效率，可以得到取能电源损耗。

需要注意的是，若式(4)、式(5)是对整个基波周期进行积分与平均，得到器件电流平均值与均方根值，则在计算器件通态损耗、开关损耗时，不再需要进行式(10)、(13)的折算，可直接在整个基波周期内积分得到通态损耗、以子模块投切频率代替器件开关频率计算开关损耗，这在IGBT-MMC中是可行的。但是，由于IGCT的门极驱动功率的计算公式(20)中含有独立的f项与I项，这样的方式会导致门极驱动功率计算不准确。

5 IGCT-MMC损耗分析算例

5.1 损耗分析依据

本文基于表2所示的数据开展分析。

表2 某直流背靠背项目参数Tab.2 Parameters of a DC back-to-back project

所选用的IGCT器件为国内某半导体公司生产的CAC5000- 45Plus，反并联二极管为德国某公司生产的D4600U，相关参数分别如表3—4所示。

表3 所用IGCT的特性参数Tab.3 Characteristic values of IGCT used

表4 所用二极管的特性参数Tab.4 Characteristic parameters of FWD used

为充分保护功率半导体器件，选用了0.6 μH感值的阳极电抗，以将IGCT开通过程的di/dt降至4 kA/μs以下，该电抗直流电阻40 mΩ。计算中，控制板卡功率取5 W，取能电源转换效率取80%。

5.2 损耗分析结果

采用平均值等效的方法，用MATLAB编程计算IGCT-MMC子模块损耗，计算结果如表5所示。为验证基于平均值等效的损耗分析方法的可靠性，表中还将平均值等效计算与模拟实际投切过程进行仿真计算得到的器件损耗结果进行了对比，并以仿真计算结果为基准计算了相对误差。

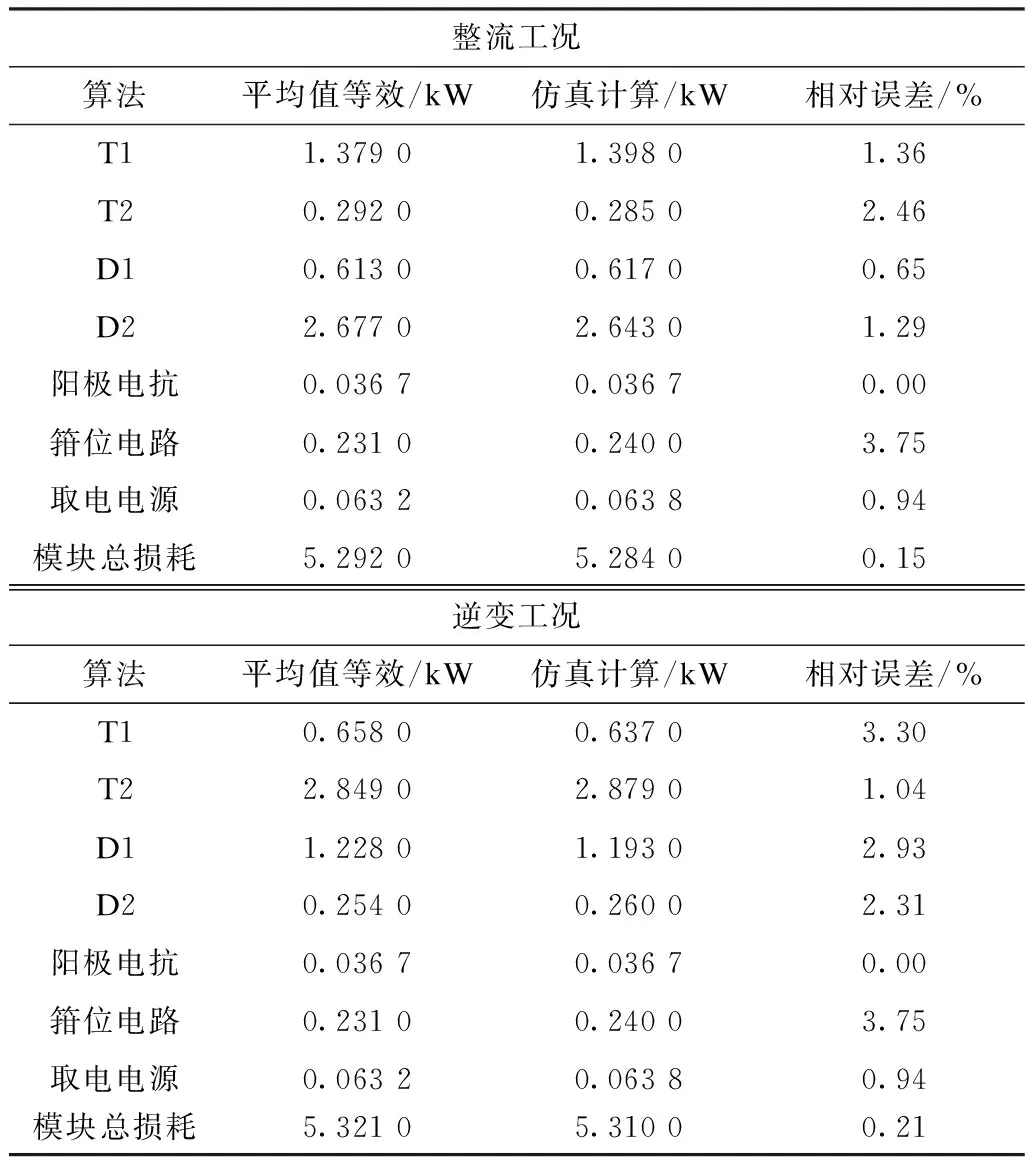
表5 不同算法损耗计算结果与比较Tab.5 Loss calculation results by different algorithms and their comparison

MMC的桥臂电流存在直流偏置，且特定功率因数下，桥臂电流、电压相位差固定，这导致各器件通流情况差异较大。以MMC逆变工况为例，桥臂电压、电流如图5所示。可以看出，桥臂电流直流分量为正，而电流正向时又对应较低的投入占比，这使得T2器件电流很大，从而其损耗显著偏高。

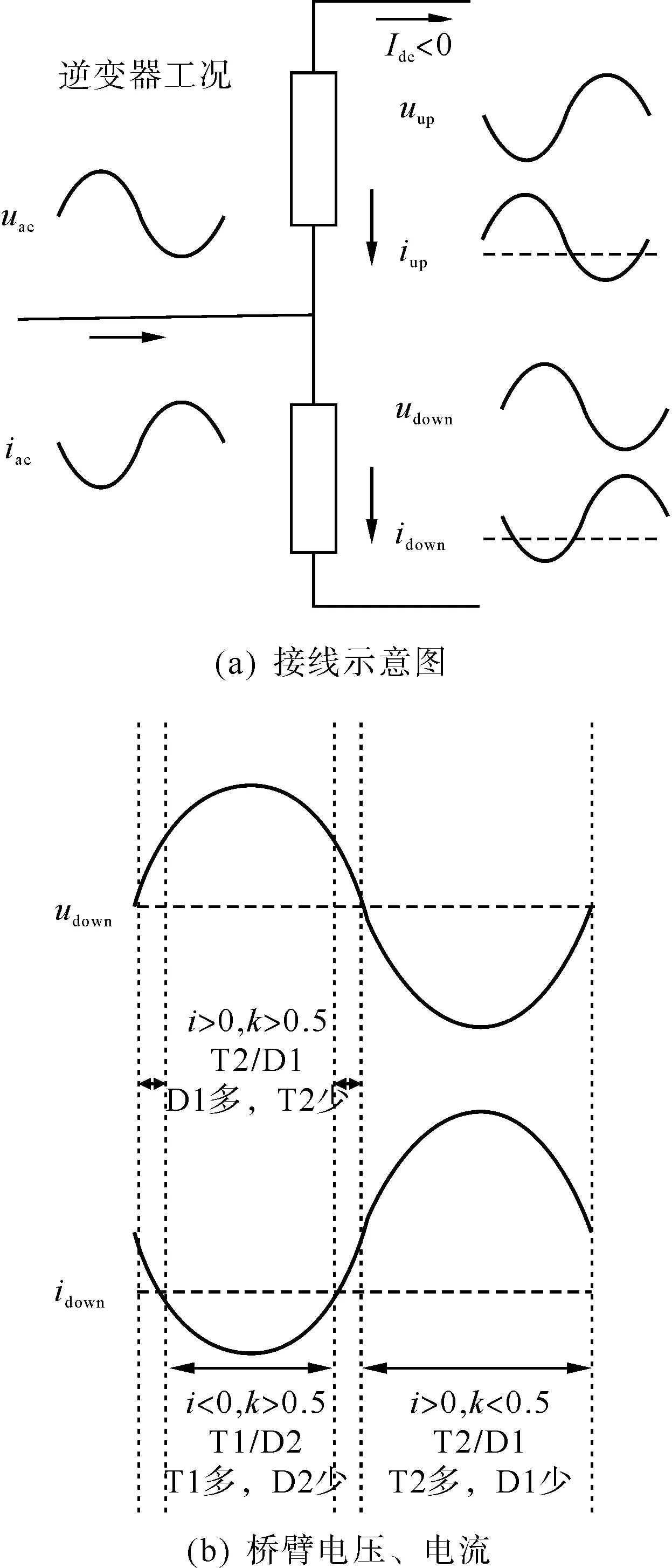
图5 MMC逆变工况下桥臂电压、电流示意Fig.5 Voltage and current of bridge arms in MMC inverter mode

与仿真计算相比，平均值等效计算的各项结果误差均在4%以内，而模块总损耗误差不到1%，这是由于仿真计算中，投切过程并不随机，导致模拟出的器件投切时刻较理想模型有所偏差，又因为各个器件特性参数相近，这种偏差在计算总损耗时部分抵消了。对于不涉及具体投切时刻，仅根据电流计算的项目，如阳极电抗损耗、取能电源损耗，平均值等效模型都有较低的误差，

总体看来，平均值等效模型具有很好的准确性。