融合了K近邻与密度峰值算法的K-means算法

王炜唯 周云才

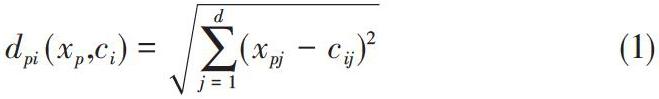
摘要：初始聚类中心的随机选择，根据主观经验确定类簇数等问题时常伴随着原始K - means算法。为了攻克以上问题，改进算法采用峰值法以及融合了K近邻算法的密度峰值算法逐一调整。通过在UCI数据集上测试及与原始K - means算法、最大最小距离距离算法在准确率、稳定性和处理数据速率方面的比较，其中最为突出的是，改进算法的准确率达到了96%以上。

关键词：K-means算法;PCA降维;峰值法;KDPC算法

中图分类号：TP301.6      文献标识码：A

文章编号：1009-3044（2021）08-0182-03

Abstract：The random selection of the initial clustering centers， and the determination of the number of clustering based on subjective experience often accompany the original K-means algorithm. In order to overcome the problems， the algorithm used Peak method and the fusion of the density peak algorithm and K-nearest neighbor algorithm to adjusted K-means algorithm. The most prominent of these is that the accuracy of the improved algorithm has reached more than 96% through testing on the UCI dataset and comparing with the original K-meaning algorithm， the maximum and minimum distance algorithm in terms of accuracy， stability and processing data rate.

Key words： K-means algorithm; shannon entropy; improved DPC algorithm

1 引言

近年來，数据大爆炸引发了人们对数据分析的需求，数据挖掘技术应运而生。而K-means算法在数据挖掘中处于重要地位。因其具有简单易懂、容易实现、时间复杂度低，处理庞大数据集效率更高等优点，所以在工作中常常成为首要的选择。然而在该算法也会产生不容忽略的问题[1-4]：①类簇数需要根据经验人工确定;②初始类中心的选择是随机的。

针对上述的不足，本文对算法做了以下改进：首先利用香农熵改进欧式距离计算公式，提高样本点相似度计算的精度;其次同时使用峰值法、融合了K近邻算法的密度峰值算法（简称KDPC算法）自动确定类簇数及精准的初始类心。论文的实验数据显示，改进后的算法（简称KDPCK-means算法）聚类结果十分贴近真实数据分布，算法性能较高。

2 原始K-means算法

2.1 原始K-means算法原理

K-means算法是经典的无监督聚类算法[5-7]，在对数据处理前无须知道数据真实类别，直接以数据相似度判断函数来估量数据间的相似度，将整体未知类别的数据集划分成不同的数据簇。K-means 算法的执行过程是：

1） 根据对数据集X的先验知识，确定数据集X的类簇数k;

2） 在X中随机选取k个数据点作首次聚类的k个类簇的类心ci（i = 1，2，...，k），同样地，每个聚类中心也有d维属性即cij（j = 1，2，...， d）;

3） 计算除类心点以外的剩余数据对象与这k个类心的相似度，根据计算结果，将这些剩余数据对象分配给最相似的那个类心所属类别，最终形成k个类簇Ci。相似度计算一般使用欧式距离计算公式：

4） 重新计算各个新得到的类簇Ci中所有数据对象d个维度的均值，将计算结果赋值给聚类中心。然后重复步骤c、d直至聚类目标函数收敛。目标函数的定义如下：

式中的x代表属于簇Ci的所有数据对象。

2.2 原始K-means算法缺陷分析及改进

根据2.1节中的算法思想可知，原始K-means算法存在诸多如下缺陷。

1） 数据集的最佳聚类数k根据对数据的先验知识确定，缺乏客观科学性。针对该问题，本文提出峰值法来决此问题。

2） 本文利用原始K-means算法对10维以上数据集聚类时发现，该算法对10维以上的数据集聚类效果很差，因此本文在面对高维数据集时，先对其降维处理，以便得到较好的聚类效果。

3） 当初始聚类中心选到含有相同类簇的数据对象时，聚类结果将会偏离真实数据分布情况，生成局部最优解。针对该问题，本文利用融合了K近邻算法的密度峰值算法加以解决。

3 原始K-means算法的改进

3.1 峰值法确定数据集的最佳类别

实验证实，最佳聚类数范围为[2，Int（[n]）][8]。本文经过大量实验发现以Calinski-Harabasz系数（CH）为指标，得到各数据集的最佳聚类数最准确。同时，由于K-means算法对高维数据集聚类效果差，本文在对高维数据集聚类前采用能最大保留数据信息的PCA降维。峰值法选取最佳聚类数的过程如下：

1） 判断数据集维数，若数据集超过10维，先对数据集采用PCA降维，然后计算数据集的最佳聚类数范围;

2） 在该范围内取不同的整数k值，对每个确定的k值用原始K-means算法对该数据集聚类10次，得到不同k值对应的最佳CH值。CH系数定义如下：

Ci表示簇Ci的类心，ni表示簇Ci拥有的数据总数，cM表示整个数据集的中心即均值，n表示整体数据集的数据数，即CH值越大，聚类效果越好。

3） 根据b步骤，以k为横坐标，CH系数为纵坐标，画出对应的折线图，选择图中的峰值点对应的k值即为该数据集的最佳类别数。

3.2 KDPC算法

根据大多数据集中样本点的分布可知，类心常被其他样本点环绕，且各个类心之间相隔较远。而这一特点正好符合DPC算法应用的前提条件。因此该算法可以很好地解决原始K-means算法中首次聚类类心随意选择的问题。然而该算法在计算样本点局部密度值时未考虑邻近样本点的分布且在选取初始聚类中心时，仍依赖人工选择，因此本文提出KDPC算法，具体过程如下：

1） 样本点局部密度的计算：

（1）  引入参数K结合赋权欧式距离来计算截断距离dc：

上式中的N代表样本点总数，（4）式表示距离样本点i最邻近的第K个样本点间的赋权欧氏距离，（6）式等号右边的第二项是每个样本点的第K最邻近赋权欧氏距离与所有样本点的第K最邻近赋权欧氏距离的均值的标准差。

2） 样本点i的距离计算：

根据上式结果，将其降序排列，然后以γ为纵轴，点的标号为横轴，建立平面直角坐标系。靠近近横轴、更平滑密集是非类簇中心，而类簇中心远离横轴，且相对分散，类簇中心点与非类簇中心间界限较明显。在自动选取初始类心前需要结合3.1节的峰值法选择排在前k位的点作为初始类心。

4 实验

4.1 实验概述

本文在下图所示的数据集上，通过与原始K-means算法、最大最小距离聚类算法的准确度、稳定性和收敛速度的比较来检验KDPCK-means算法的改进是否有效。

4.2 实验展示与分析

由于文本篇幅限制，下文主要展示本文算法在Iris数据集上的运行效果。

由图1可知：Iris数据集有3个γ值凸出的间断点，最佳聚类数为3，将前3个最大的γ值点作为Iris数据集的初始类心。

由表2可知，KDPCK-means算法得到的初始类心、最终类心与Iris数据集真实类心十分接近。

在这两种数据集中，KDPCK-means算法的精确度显优于前两种算法，其迭代次数也明显少于前两种算法。通过以上实验数据可知，KDPCK-means算法在一举解决了原始K-means算法中问题的同时，在准确率、稳定性及运行效率上都得到了有效的提升。

参考文献：

[1] Al Hasib A，Cebrian J M，Natvig L.A vectorized k-means algorithm for compressed datasets：design and experimental analysis[J].The Journal of Supercomputing，2018，74（6）：2705-2728.

[2] Douzas G，Bacao F，Last F.Improving imbalanced learning through a heuristic oversampling method based on k-means and SMOTE[J].Information Sciences，2018，465：1-20.

[3] García J，Crawford B，Soto R，et al.A k-means binarization framework applied to multidimensional knapsack problem[J].Applied Intelligence，2018，48（2）：357-380.

[4] Manju V N，Lenin Fred A.AC coefficient and K-means cuckoo optimisation algorithm-based segmentation and compression of compound images[J].IET Image Processing，2018，12（2）：218 -225.

[5] 陳思敏.基于位置指纹识别的WiFi室内定位算法研究与实现[D].南京：南京邮电大学，2016.

[6] 韩雅雯.kmeans聚类算法的改进及其在信息检索系统中的应用[D].昆明：云南大学，2016.

[7] 孔超.基于分布式平台的高校网络舆情分析系统研究与实现[D].成都：电子科技大学，2017.

[8] 郭靖.K-means聚类算法改进研究[D].北京：中国人民公安大学，2018.

【通联编辑：李雅琪】