基于小波降噪和自适应加权法的温室数据融合

朱垲 宋欣 何建祥 杨磊

摘要：针对温室环境信息多节点数据采集中存在误差大、冲突多和冗余等问题，提出一种基于小波降噪和自适应加权的多传感器数据融合算法。通过小波降噪对采集的数据进行处理，使其具有良好的光滑度和稳定性;利用自适应加权算法对多传感器数据进行融合，得到测量数据的最优估计值。实例验证结果表明，采用所提算法可以有效降低原始数据中存在的噪声和冗余，得到方差较小的数据融合值，可以提高测量数据的准确性和降低数据的传输量;具备良好的稳健性，能够实现对温室环境信息的可靠性和一致性描述。

关键词：多传感器;数据融合;小波降噪;自适应加权算法;温室

中图分类号：S126 文献标志码： A

文章编号：1002-1302（2021）05-0180-06

近年来，随着我国温室生产的大面积推广与应用，如何实现对温室环境的优化调控，为农作物生长提供适宜的环境，达到优质、高效和低耗的生产目的[1]，已逐渐成为研究热点。温室作为一个复杂的热力学系统，具有多变量、滞后性、时变性、非线性和强耦合等特点[2]，传统控制方法难以实现对温室环境的精准调控。目前普遍采用的是智能控制方法，如模糊控制、神经网络、多目标优化等，以及多种方法交叉融合的混合控制。这些方法都是以精确的温室环境模型作为基础[3]，而温室环境模型的精确构建则要依赖于环境信息采集的鲁棒性和容错性。

因为温室内各点环境信息分布不均匀，同时也为了克服单点采集存在的不确定性和局限性，对同一个环境参数通常要进行多点采集。但由于外部环境和传感器内部构造等多种因素的影响[4]，采集到的多组数据中往往存在异常值、数据缺失、误差大、冲突多、信息冗杂等问题，严重影响了数据的一致性和可靠性[5]。因此，有必要通过数据融合技术对采集到的数据进行处理，得到温室环境信息完整且一致性的描述，从而提高环境信息的鲁棒性和稳健性，以实现温室环境的精准调控。同时，也有助于减少数据传输量，提高控制系统的工作效率，降低无线传感器网络能耗。

目前，数据融合技术在设施农业环境控制方面的应用已取得了一些研究成果。熊迎军等提出在对采集数据进行一致性检测和3次指数平滑的基础上，利用一种新型支持度函数进行幂均方融合的方法，能够在得到较高融合精度的同时缩短算法的运行时间;但是该方法在对数据进行预处理时，采用分布图法对异常数据进行了剔除，会导致样本数据的减少，以及异构传感器间样本数量的不一致，从而影响后续的融合精度[6]。初洪龙等提出了基于信任度的多传感器数据融合方法，利用自定义的指数信任度函数，分配每个传感器数据的权重，实现多传感器的数据融合[7];但指数运算相对复杂，开销大，不适用于温室无线传感器网络。王振等在利用狄克逊准则对采集数据进行预处理的基础上，采用卡尔曼滤波和基于最小二乘法原理的加权方法实现了数据融合，并通过丢包补偿策略提高了融合进度[8]。该方法仍旧存在剔除数据所导致的样本数量减少问题，而且卡尔曼滤波的融合效果过于依赖状态空间模型的精确性。此外，还有将聚类分析、模糊理论与专家系统相结合的融合方法，但专家系统依赖于一定的先验知识，才能够进行推理。

针对上述问题，本研究提出先采用小波降噪对采集的数据进行处理，使数据序列具有良好的光滑度和稳定性;然后利用自适应加权算法对多传感器数据进行融合，从而实现对温室环境信息的可靠性和一致性描述。

1 温室环境采集数据的小波降噪

由于小波分析适用于由短时高频成分和长时低频成分组成且无太多先验知识的数据进行降噪处理[11]，故可用于对温室环境信息采集数据的处理。此外，由于采集温室环境参数会受限于传感器的布置以及使用成本，采集节点相对较少，所获得的监测数据样本有限，故采用小波分析法还能充分利用采集的数据，避免剔除数据所造成的样本数据减少和不一致问题。小波降噪的处理过程如下：

（1）小波分解：选择适当的小波基函数，确定分解层数，并利用Mallat算法对原始数据进行分解;设原始数据为f（x），则在尺度j下的低频部分为Adjf，高频部分为Djf，以0级为最高分辨率方向，则原始数据最终可被分解为

f（x）=Ad-Jf+∑-1j=-JDjf。（1）

式中，J为分散层数，一般取值为5或6。

（2）高频系数的阈值量化：选定合适的阈值对第1层至第N层的高频系数进行量化处理;

（3）小波重构：根据小波分解的第N层低频系数和经过量化处理后的第1层至第N层高频系数进行小波重构，得到降噪后的离散数据。

2 自适应加权融合算法

2.1 自适应加权融合算法的基本原理

自适应加权融合算法的基本原理[13]如图1所示，以总均方误差最小的为最优条件，依据每个传感器的测量值xi（i=1，2，3，…，m ），以自适应方式获得其最优权重wi（i=1，2，3，…，m ），使得最終的融合结果 x^达到最优。该算法能够有效综合多传感器的测量信息，并具有算法简洁、无需先验知识、实时性好等优点，适用于温室环境信息的数据融合[14]。

融合结果 x^ 和各传感器权重wi满足如下关系：

x^=∑mi=1wixi

∑mi=1wi=1。（2）

总均方误差（σ2）为

σ2=E^）2〗=∑mi=1w2iσ2i。（3）

式中：σ2i（i=1，2，3，…，m）为各传感器的方差;x为温室环境参数的真值，各传感器的测量值为xi彼此相互独立且为x的无偏估计。

根据自适应加权算法的基本原理可知，当总均方误差σ2为最小值时，其对应的各传感器权重wi为最优，因此，采用拉格朗日乘数法对公式（3）求极值，得到极点：

wi=1σ2i∑mi=11σ2i。（4）

此时，对应的最小均方误差为

σ2min=1∑mi=11σ2i。（5）

最终数据融合结果为

x^=∑mi=1xiσ2i∑mi=11σ2i。（6）

2.2 传感器方差的求解

利用各传感器所测数据间的相关性对方差进行求解。设2个独立的传感器p和q，其待估计真值为x，采样数据分别为xp、xq，其对应的测量误差分别为ep、eq，且为零均值的平稳噪声，则有

xp=x+ep

xq=x+eq。（7）

传感器p的方差可表示为

σ2p=E。（8）

xp、xq的互协方差（Rpq）为

Rpq=E=E。（9）

xp的自协方差（Rpp）为

Rpp=E=E+E。（10）

由公式（8）、公式（9）、公式（10）可得：

σ2p=Rpp-Rpq。（11）

设传感器在k时刻时，Rpp和Rpq的时间域估计值分别为Rpp（k）、Rpq（k），则有：

Rpp（k）=1k∑kj=1xp（j）xp（j）=k-1kRpp（k-1）+1kxp（k）xp（k）。（12）

Rpq（k）=1k∑kj=1xp（j）xq（j）=k-1kRpq（k-1）+1kxp（k）xq（k）。（13）

Rpq可用Rpq（k）的均值Rpq（k）進行估计：

Rpq=Rpq（k）=1m-1∑mp=1q≠pRpq（k）。（14）

由此可知，各传感器方差可通过自协方差Rpp和互协方差Rpq的时间域估计值进行估计。

3 实例分析

试验数据采集自辽宁省某温室试验基地，以2019年3月1日采集到的温度、湿度数据为样本，进行算法验证。温室中按照一定距离间隔分别布置2个传感器节点，每隔30 min采集1次数据，共采集48组样本。

3.1 小波降噪预处理

利用Matlab软件对样本数据进行小波降噪处理。通过多次试验结果对比，最终选择db5小波基函数进行3层分解，各层阈值选用软阈值函数，阈值估计采用RigrSure阈值法，降噪重构后的数据与原始样本数据的对比结果如图2所示。

从图2-a、图2-b可以看出，温度曲线在中间时段存在较大波动，经过小波降噪处理后的数据曲线无奇异值出现，具有良好的光滑度和稳定性，起到了很好的降噪效果。

3.2 多传感器数据融合

根据“2.1”节中所述的自适应加权融合算法的基本原理，利用Matlab软件实现其求解过程。在权重求最优解时，各传感器权重会随着采样次数的增加而变化，当样本数量达到一定数值时，权重会趋于稳定，并最终收敛于某一数值。如图3-a所示，温度权重大约在样本数量为40时趋于稳定，最终分别收敛于0.53、0.47。如图3-b所示，湿度权重大约在样本数量为35时趋于稳定，最终分别收敛于0.52、0.48。表1所示为收敛后，满足总均方误差最小条件的各温度、湿度传感器权重的最优解，及其对应的最小均方误差。可以看出，融合后的总均方误差要低于各个传感器的方差，证明经过数据融合可以得到各测量值的最优估计，从而提高传感器数据的准确性。

将融合算法与算术平均法的融合效果相比（图4）可以看出，应用所提算法得到的融合曲线比算术平均法融合曲线更加光滑，数据波动小，具有很好的稳定性。为了进一步对比融合效果，分别计算了2种融合结果的标准偏差进行比较，如图5所示，采用本研究所提算法得到的融合结果，其标准偏差曲线更加平滑和稳定，从而证明其融合结果更加可靠。

3.3 算法稳健性验证

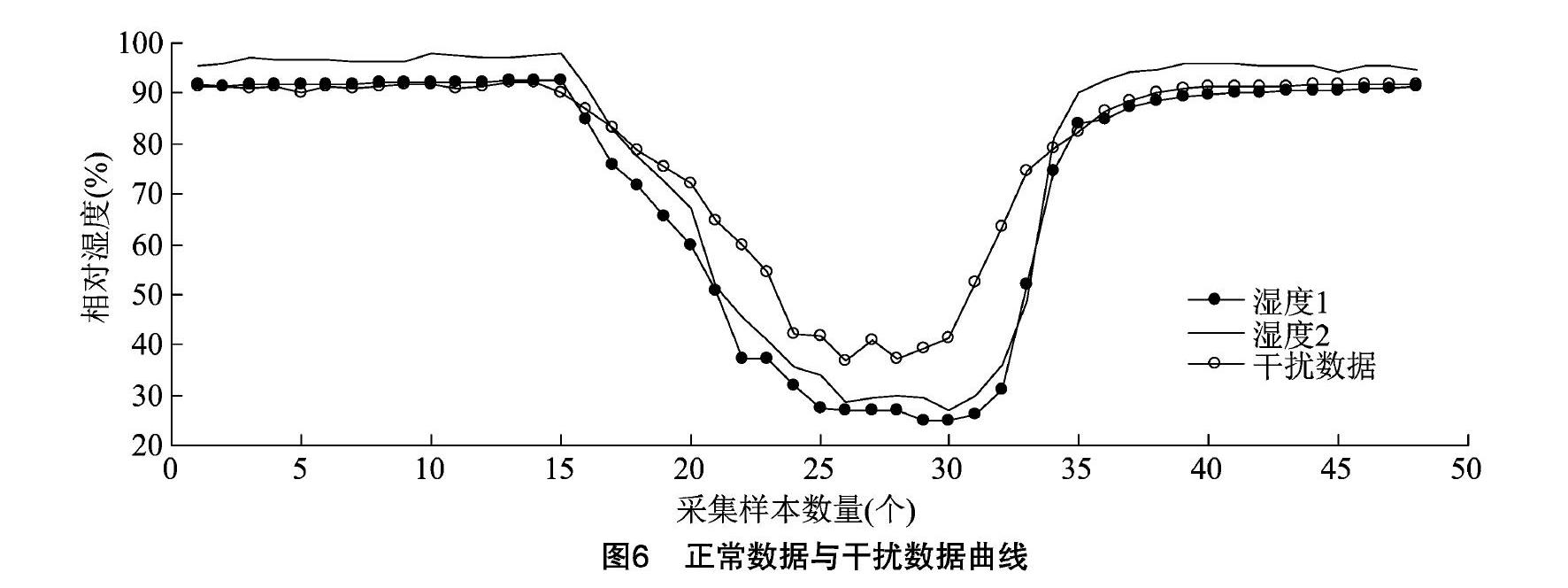
为验证本研究算法的稳健性，增加1组2019年3月3日的湿度数据作为干扰数据，模拟采集数据存在异常值的情况。从图6可以看出，干扰数据相比正常样本数据最大偏差为35.7%，存在一定偏离，能够起到干扰效果。

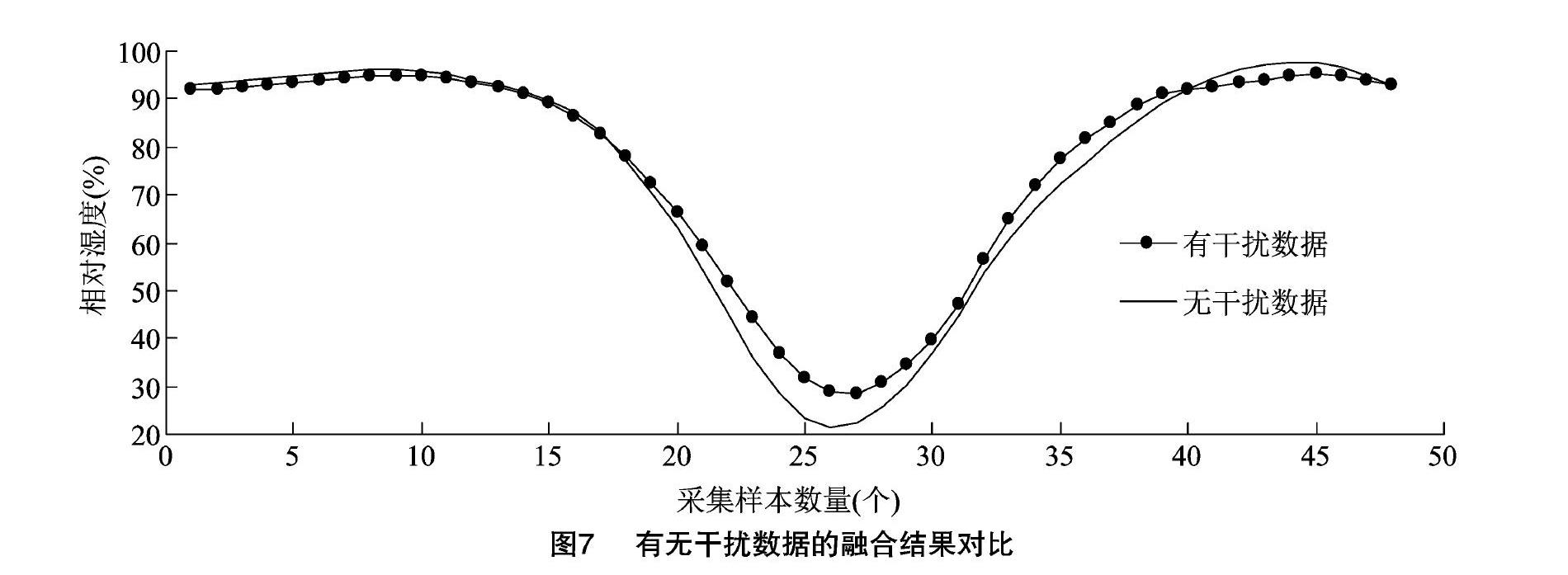
从图7可以看出，存在干扰数据的融合曲线依然具有较好的光滑度，并且与无干扰数据融合曲线趋势相一致，由此证明采用本研究所提算法在遇到异常值情况下具有较好的稳健性。

4 结论

针对温室环境信息多节点数据采集中存在误差大、冲突多和冗余等问题，本研究提出了一种基于小波降噪和自适应加权相结合的多传感器数据融合算法。通过实例对所提算法的可行性进行了验证，并且与算术平均法的融合效果，以及加入干扰数据后的融合效果逐一进行了对比，结果表明采用本研究所提算法可以有效地降低原始数据中存在的噪声和冗余，得到方差较小的数据融合值，提高测量数据的准确性和降低数据的传输量;具备较好的稳健性，能够实现对温室环境信息的可靠性和一致性描述，为后续温室环境建模提供可靠的数据。

参考文献：

[1] 毛罕平，晋 春，陈 勇. 温室环境控制方法研究进展分析与展望. 农业机械学报，2018，49（2）：1-13.

[2]赵春江. 精准农业研究与实践. 北京：科学出版社，2009.

[3]张雪花，张 武，杨 旭，等. 农业温室环境控制方法研究综述. 控制工程，2017，24（1）：8-15.

[4]孙力帆，张雅媛，郑国强，等. 基于D-S证据理论的智能温室环境控制决策融合方法. 农业机械学报，2018，49（1）：268-275.

[5]Chen Y K，Si X C，Li Z G.Research on Kalman-filter based multisensor data fusion. Journal of Systems Engineering and Electronics，2007，18（3）：497-502.

[6]熊迎军，沈明霞，陆明洲，等. 温室无线传感器网络系统实时数据融合算法. 农业工程学报，2012，28（23）：160-166.

[7]初洪龙，马玉强. 基于信任度的多传感器数据融合在农业物联网的应用. 农业网络信息，2017（12）：130-132.

[8]王 振，白星振，马梦白，等. 一种基于数据预处理和卡尔曼滤波的温室监测数据融合算法. 传感技术学报，2017，30（10）：1525-1530.

[9]温 静. 多传感器数据融合技术在温室控制中的应用. 河北农业大学学报，2015，38（4）：111-115.

[10] 王宪磊，裴玖玲，刘润泽，等. 南疆地区智能温室控制系统研究——基于多传感器融合机理. 农机化研究，2017，39（7）：39-42，57.

[11]田胜利，周拥军，葛修润，等. 基于小波分解的建筑物变形监测数据处理. 岩石力学与工程学报，2004，23（15）：2639-2642.

[12]邸继征. 小波分析原理. 北京：科学出版社，2010.

[13]翟翌立，戴逸松. 多传感器数据自适应加权融合估计算法的研究. 计量学报，1998，19（1）：69-75.

[14]孙国祥. 基于多信息融合的温室黄瓜肥水一体化灌溉系统研究. 南京：南京农业大学，2016.