基于多目标随机森林的煤层厚度同步预测方法
2021-04-22刘晓明
刘晓明,王 新,徐 慧
(中国矿业大学 计算机科学与技术学院,江苏 徐州 221116)
0 引 言
构造煤是由原生结构的煤层在构造应力作用下,发生了结构和成分显著变化而形成的一种煤体[1]。目前,在我国对能源的需求不断加大的背景下,越来越多的复杂矿井已经开始投入生产,同时煤矿的开采范围及深度也在不断的增加。虽然煤矿提高了产量,但也使得瓦斯危害的问题越来越突出。因此,如果可以根据构造煤厚度及其分布来划分煤矿瓦斯突出区域[2],也就能减少事故的发生,保障煤矿生产的安全。目前,很多机器学习的方法被应用到煤层厚度预测和构造煤厚度预测中,如:模糊神经网络、极限学习机等[3,4]。众多学者多致力于单一目标的煤层或构造煤层厚度预测,如果能够同步预测出煤层和构造煤的厚度,以此划分出煤与瓦斯危险区域,就能为煤矿的开采提供可靠的保障。多目标预测是一个活跃且快速发展的研究领域,多目标回归(MTR)目前已经应用在到很多领域,如生态模型预测、水文模型预测[5,6]等。多目标回归相比为每个目标构建单独的回归预测模型,主要有两个优点。首先,构建单个多目标回归模型通常比对所有变量单独构建回归模型总规模小;其次,多目标回归模型能更好地识别不同目标变量之间的依赖关系。
多目标随机森林MTRF(multi-target random forest)是一种多目标预测方法,它是以决策树为基本分类器的集成学习算法,通过对训练数据以及特征的自采样来构建预测模型。对于多目标学习,随机森林子模型不是建立单目标回归模型,而是建立多目标回归模型。具体而言,它基于随机选择特征集的多目标决策树构建多目标随机森林。本文构建了多目标随机森林的预测模型,利用遗传算法中的核心思想改进粒子群算法,最终使用改进后的优化算法对模型参数进行优化,对研究区域煤层和构造煤厚度进行同步预测。
1 基本原理
1.1 随机森林
随机森林(random forest,RF)是预测分析最有效的机器学习模型之一,使其成为机器学习的工业主力。随机森林预测器[7]是一个集成预测器,它结合了套袋和随机特征子空间,用于构建决策树的准确分类或回归集合。套袋和随机子空间本身都是有效的集成方法,它们都增加了分类器的多样性,并有效地学习相当准确的预测模型。
在预测期间,每个单独的集合成员投票选择最适合其有限范围的预测,然后使用聚合方法组合这些投票以计算最终的预测结果。随机森林模型是一种加性模型,它通过组合一系列基础模型的决策来进行预测。将这类模型编写为f1(x),f2(x),…,fn(x), 最终的模型g(x) 是由这n个基础模型共同决定的。这里,每个基本分类器都是一个简单的决策树。这种使用多个模型来获得更好预测性能的广泛技术称为模型集成。在随机森林中,所有基础模型都是使用不同的数据子样本独立构建的。
1.2 粒子群算法
粒子群算法(particle swarm optimization,PSO)是最初由Kennedy和Eberhart提出的一种模拟社会行为的优化算法[8],粒子群算法主要受到鸟类觅食行为的启发,通过粒子间的相互作用,最终寻找到搜索空间中的最佳点或几个最佳点的周围。
PSO算法初始化搜索空间X=(X1,X2,X3,…,Xn), 设Xi粒子为D维向量Xi=[Xi1,Xi2,Xi3,…,XiD]T。 通过适应度函数计算每个粒子对应的适应度。设第i个粒子的飞行速度为vi=[vi1,vi2,vi3,…,viD]T, 其个体极值为pbi=[pbi1,pbi2,pbi3,…,pbiD]T, 全局极值为gbi=[gbi1,gbi2,gbi3,…,gbiD]T。 粒子在迭代中通过式(1)、式(2)更新自身的速度和位置
vid=ω×vid+c1rand()(pbid-xid)+
c2rand()(gbid-xid)
(1)
xid=xid+vid
(2)
其中,ω为惯性权重;d=1,2,3,…,D;i=1,2,3,…,n;k为迭代次数;vid为当前粒子速度;c1和c2为非负常数。
1.3 遗传算法
遗传算法在20世纪70年代由密歇根大学的John Holland在美国正式引入,是基于遗传学和自然选择原理的优化技术。遗传算法(genetic algorithm,GA)在本质上是充分随机化的,但是它比随机局部搜索表现得更好。
GA算法的原理是模拟生物的进化过程,通过选择、交叉、变异等[9]操作产生下一代的解,并逐步淘汰适应度低的解,以此接近问题的最优解。进化M代后就很有可能进化出适应度很高的个体,即最优解的近似解。
遗传算法运算过程:
步骤1 种群初始化:计数器t=0, 进化代数T, 并随机生成M个个体作为初始种群P(0)。
步骤2 适应度计算:通过适应度函数计算种群P(t) 中每个个体的适应度,使用该适应度表征群体中每个个体的优异程度。
步骤3 选择:从群体中选择出优异个体,使其更有机会遗传到下一代,这是根据个体的优异程度来选择的。
步骤4 交叉:对群体中部分个体使用交叉运算得到下一代个体,它们继承了父代的基因。
步骤5 变异:对群体中部分个体使用变异运算。对这些个体,以变异概率改变某几个基因值,改变值为其它个体的同位基因。
步骤6 终止判断:若t=T, 则最优解为运行过程中得到的最优适应度个体,否则返回步骤2。
1.4 预测评价指标
均方根误差(RMSE)是残差的标准偏差(预测误差),式(3)是本文用来比较多目标学习算法的性能的度量
(3)
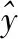
2 基于多目标随机森林的煤层厚度和构造煤厚度预测模型
2.1 预测模型
对多目标进行符号描述,设X和Y为两个随机向量,假设训练集由M个实例组成,即 {(x1,y1),(x2,y2),…,(xm,ym)}。
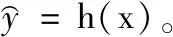
采用多目标随机森林算法对训练数据构建模型,预测过程如图1所示。

图1 基于随机森林回归算法的煤层和构造煤厚度预测模型
随机森林利用Bootstrap方法对训练样本集(x,y)train中进行n次自采样,组成n个样本个数为m的子集,每个子集都模拟了真实样本的分布,对每个样本分别构建多目标回归树,最终的模型就是这多个预测器的组合。
2.2 算法步骤
随机森林的基础回归器的选择有很多,比如CART树[10]、PCT(predictive clustering tree)[11]、CI树(conditional inference trees)[12]等作为基础预测器,只要满足“随机性强”、“不稳定”特征的多目标回归预测器都可以成为随机森林的子模型,本文利用的是单变量递归分区方法(CART)对多输出回归问题的扩展。因此,多变量回归树是按照与CART相同的步骤构建的,即从根节点中的所有实例开始,然后迭代地找到最佳分割并相应地分割叶子直到预定义的停止标准到达。与CART的唯一区别在于使用多变量的平方误差之和重新定义单个节点的不纯度[13]
(4)
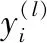
随机森林模型的参数需要通过经验选取,并没有理论上的支持,本文将一种混合优化算法GAPSO引入随机森林模型,对模型中的参数进行迭代优化。
遗传算法虽然由于其随机性,对全局的搜索能力较强,但局部的搜索能力较弱,同时遗传算法在后期的进化过程中效率较低,对于已经学习到的解记忆较差。而粒子群算法虽然对于优秀的解都保存下来,但比较难处理离散问题,且由于粒子之间的相互作用,易陷入局部最小。针对这两种方法的优缺点,GAPSO算法通过对粒子群算法中的粒子增加一种进化的行为,使其在保留较强的局部搜索能力情况下,也拥有较强的全局搜索能力。
下面是GAPSO-RF算法具体步骤:
步骤1 参数初始化:设置粒子群参数速度v,位置x,种群规模popsize, 惯性权重w,进化代数T。
步骤2 计算适应度:对位置x离散化,使用适应度函数评估各个粒子的优异程度,得到每个粒子的个体最优位置pb和群体最优位置gb。如满足条件则结束循环。
步骤3 保留粒子:通过计算得到的适应度对粒子进行优异程度排序,以比例u保留表现优异的粒子。
步骤4 更新参数:对参数速度v,位置x进行更新。
步骤5 进化较差粒子:一定概率下将表现不好的粒子进行交叉和变异,加入随迭代次数减小的惯性权重,依式(5)更新参数w
(5)
步骤6 判断迭代次数:如未达到指定次数,则转步骤2。
其中是适应度函数具体步骤:
步骤1 通过Bootstarp生成n个样本子集Di(i=0,1,…,n);
步骤2 使用n个决策树模型分别对各个子集进行训练,在训练过程中,随机性地选择特征;
步骤3 将生成的决策树进行合并,形成一个集成的预测模型;
步骤4 将验证集代入集成的模型,得到验证集的预测结果,输出预测指标RMSE。
本文GAPSO算法参数设置:粒子数量为10,加速常数为0.9,惯性常量初始为0.9,随迭代降至0.1,粒子保留率为0.4,非优异粒子仍保留至下代概率为0.1,迭代次数为12。
3 算例分析
3.1 算例数据
本文选取的研究区域是安徽省宿州市的芦岭煤矿Ⅱ六采区8煤层。如图2所示,该地区煤矿开采困难,构造煤普遍发育,因此极易发生煤与瓦斯突出危害[14]。选用该研究区域的实际地震属性数据,同步预测出该区域的煤层厚度和构造煤厚度。
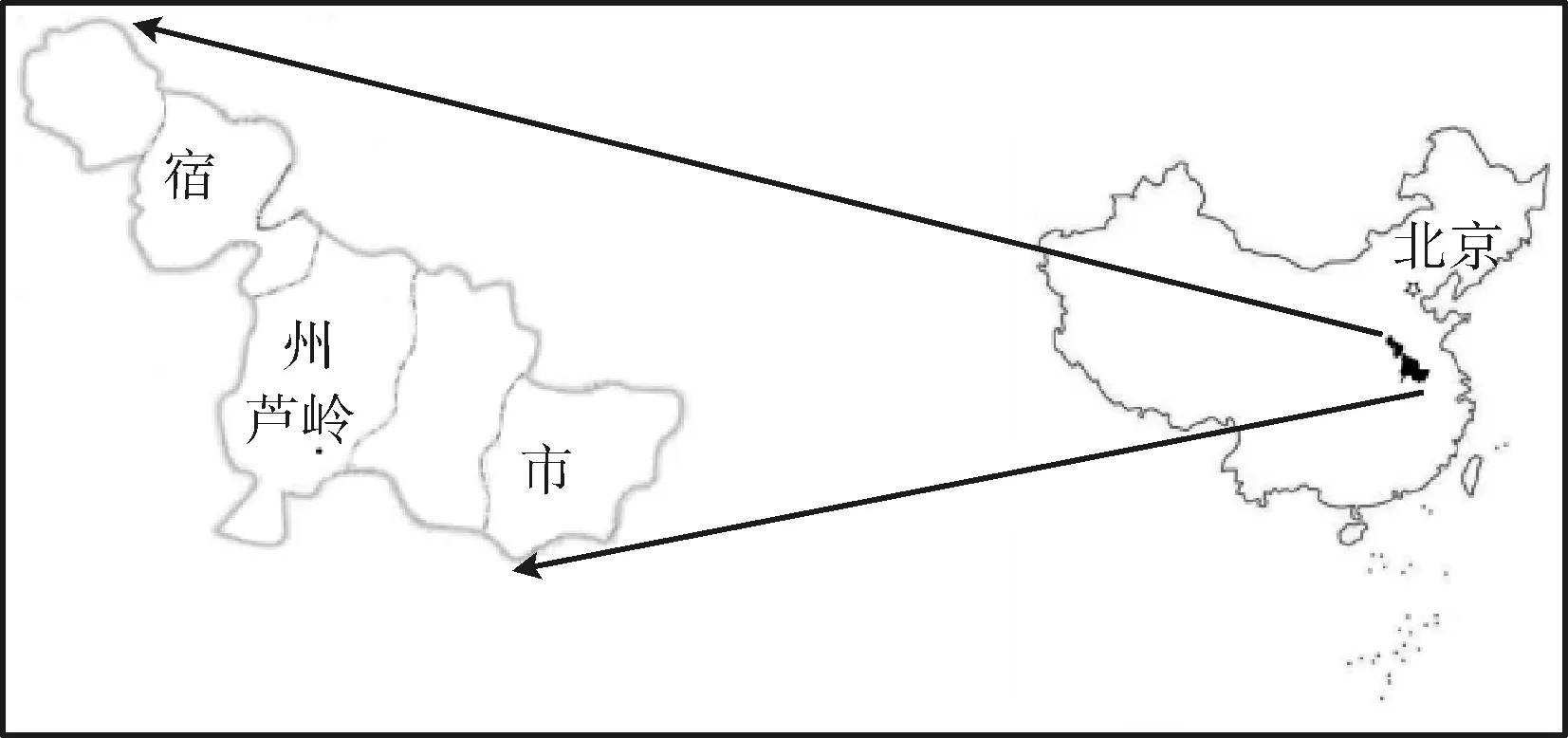
图2 矿区位置
芦岭煤矿具有特别的煤层特性和地质,使得该区域的煤与瓦斯突出问题严重,在2002年和2003年发生过两次重大事故,导致多人死亡和受伤[15]。
3.2 地震属性数据预处理
本文选取了芦岭煤矿Ⅱ六矿区8煤层与煤层厚度和构造煤厚度相关的21维地震属性数据,选用整个矿区范围内已有的17口钻孔。实验中采用主成分分析方法,对数据集进行降维处理,取累计贡献率大于95%的数据作为主成分,得到降维后的10维地震属性数据。
将降维后的地震属性数据以单棵决策树为基准,使用遗传算法得到最优预测序列为:91-5、2002-4、2002-5、2012-1、2014-5、L43、06-4、91-2、92-8、94-2、91-1、92-2、94-5、2002-3、94-1、99-1钻孔预测2010-11钻孔,其中每个钻孔的详细数据见表1。

表1 钻孔详细数据
3.3 多目标随机森林预测与传统单目标预测性能对比分析
本次实验建立的单目标预测模型依然选取随机森林作为预测模型,但选取的基础回归模型转变为单目标决策树。本文对其参数进行与多目标随机森林参数同样的优化算法,建立GAPSO-RF和GAPSO-ART模型,对随机森林的参数进行优化,包括决策树最大深度在1到50之间取值,子模型的数量在1到200之间取值,分裂所需的最小样本数在2到20之间取值,叶节点的最小样本数在1到20之间取值,特征数量选择平方根sqrt。输入模型的是通过PCA属性降维获得10个线性不相关地震属性数据。选取17口井共1815道地震属性数据作为样本进行实验,其中16口井作为训练集,1口井作为测试集,测试集有40%的数据被选入来优化GAPSO-RF和GAPSO-ART模型,目标1煤层厚度预测如图3所示,目标2构造煤厚度预测如图4所示。

图3 目标1预测结果对比

图4 目标2预测结果对比
从图3和图4分析,在到达10次迭代后,RF与ART模型的RMSE基本保持不变,意味着两个达到了最小的误差,对于目标1,RF模型的RMSE为0.224,ART模型的RMSE为0.237,对于目标2,RF模型的RMSE为0.087,ART模型的RMSE为0.296,因此优化的多目标随机森林比单目标具有更好的预测效果。
3.4 多目标随机森林预测与BP性能对比分析
本次实验建立的神经网络模型采用的是误差反向传播算法的多层前馈网络[16],是目前使用很普遍的一种神经网络。根据模型的输入参数(10个),输出参数(2个),设置单层隐藏层,隐藏层神经元个数为256个,中间层使用sigmoid函数,输出层使用relu函数,优化器使用adagrad,损失函数选用mse,建立BP神经网络模型,模型输入的数据是通过PCA属性降维获得10个线性不相关地震属性数据。选取17口井1815道地震属性数据作为样本进行实验,其中16口井作为训练集,1口井作为测试集,预测结果如图5所示。
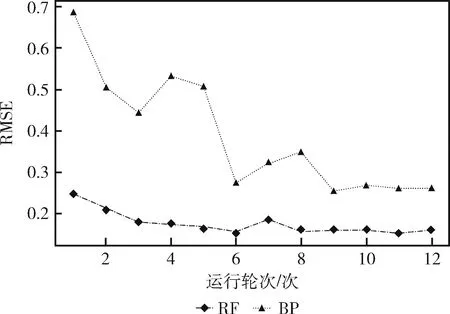
图5 RF与BP预测结果对比
从图5分析,在到达9次迭代后,BP与随机森林模型的RMSE基本保持不变,意味着两个达到了最小的误差,此时RF模型的RMSE为0.153,BP模型的RMSE为0.252,因此优化的多目标随机森林比BP模型具有更好的拟合效果。
3.5 厚度预测对比
利用改进的预测模型,对研究区域的两种煤层厚度进行预测,将3个模型分别运用到整个8煤层,GAPSO-ART,GAPSO-RF分别运行了53.2 s,41.0 s,因此构建单个回归模型比为每个目标构建回归模型所需时间短。模型都使用分别优化得到的最优参数进行预测,分别预测10次,最终得到煤层厚度预测结果见表2,构造煤厚度预测结果见表3。
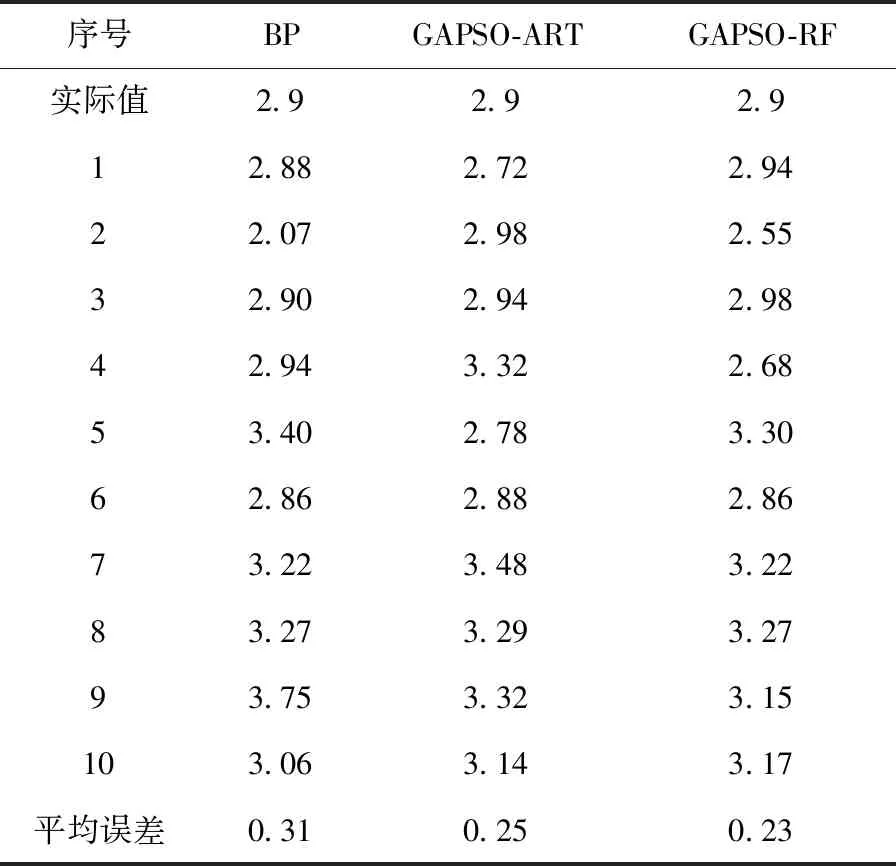
表2 煤层厚度预测结果对比
由表2、表3分析,采用多目标随机森林模型预测煤层厚度平均误差为0.23,同步预测构造煤厚度平均误差为0.08,远低于BP模型和单目标预测误差。

表3 构造煤厚度预测结果对比
4 结束语
(1)使用多目标随机森林方法预测原生煤层厚度和构造煤厚度,并将预测结果与ART和BP方法作比较,多目标随机森林方法预测精度更高,耗时也低于单目标预测方法。本文的算法通用于其它多目标预测的问题。
(2)本文提出GAPSO算法对随机森林的超参数进行优化,建立了GAPSO-RF和GAPSO-ART预测模型,通过实验验证,优化后的模型比未优化模型预测精度更高。
(3)为所有目标构建单个回归模型的规模比为每个目标分别构建回归模型的总规模小,多目标考虑了目标变量之间的相关性,最终获得了更好的预测效果。
(4)研究区域芦岭煤矿Ⅱ六采区8煤层的17口井预测的最优参数为决策树深度21,子模型的数量为150,分裂所需的最小样本数为11,叶节点的最小样本数为5。
