考虑级联失效影响的复杂网络关键节点识别
2021-04-22吴嫣媛刘向军
吴嫣媛,刘向军
(华北电力大学 电气与电子工程学院,北京 102206)
0 引 言
目前对复杂网络节点重要性判断方法都是针对具体问题提出的,存在一定的片面性和局限性,且会随着网络结构的变化使识别结果存在一定误差[1,3]。文献[4,5]指出了这种缺点,进而引入优化理论来进行关键节点识别,从攻击的角度通过节点失效后网络性能下降的方法来确定节点的重要性,以网络性能最小为目标采用禁忌搜索算法得到节点排序,使得识别方法适用于不同结构与类型的网络。但文献[4,5]在构建网络抗毁性测度衡量网络性能时,假设一个节点的失效不会影响其它节点,没有考虑拓扑结构的改变导致网络中物质流的变化,不能很好地反映真实的节点重要程度。文献[6-8]在计算节点失效后的网络性能测度时引入了级联失效过程,很好地切合了实际网络的这种动态特征。因此在关键节点识别过程中计算鲁棒性测度衡量网络性能时,应当考虑网络级联失效过程。同时文献[4,5]采用的禁忌搜索算法是一种基于单点搜索的元启发式算法,且具有对初始解依赖性较强、多样性不足等缺 点。
本文采用优化算法进行复杂网络的关键节点识别,在此基础上,考虑网络的动态性引入级联失效模型改进网络鲁棒性测度,并针对禁忌搜索算法的缺点,改进人工鱼群算法作为节点序列构造模型的求解算法,最后对比攻击不同策略识别的关键节点在模拟网络上的效果,验证本文策略的有效性和优越性。
1 级联失效模型
受制于硬件成本,每个节点都具有给定的负载容纳能力。最初,网络处于稳定状态,其中每个节点的负载小于其容量。由于节点的故障,网络受到了干扰,故障改变网络中流量的平衡,负载将重新分配给其它节点,并可能进一步导致其余节点过载,并足以引起整个系统故障。级联失效反映的是网络的动态特性,网络拓扑结构的改变造成网络数据流的重新分配,此过程描述如下[9,10]:
任何一个网络可由图G=(V,E)作抽象表示。V(G)是有限非空集,V中元素称为G的顶点,N=|V|表示网络中的节点数,E(G)是V(G)中顶点之间的边的集合。在很多情况下,常直接用介数或对介数稍加修正作为真实流量的近似值,网络的实时流量如下
(1)
B(x)用于表示节点的流量。gij(x)定义为从节点i到j经过节点x的最短路径的数量。gij是从节点i到j的所有最短路径数。此外,节点自身的数据量L也是总负载的重要组成部分。因此,节点x在时间t的负载可以表示为
(2)
其中,Lx(t)表示在时间t节点x的总负载,L为节点x的自身负载。由于大多数网络节点的承载有限,将节点负载的上限定义为容量Cp,是节点过载和性能降低之前可以处理的最大负载,用时间t=0时的负载Lx(t)乘以容忍系数T表示
Cp=T·Lx(0),x=1,2,…,N
(3)
其中,T≥1。当在时间t-1处节点x的流量负载超过Cp时,在时间t处节点将过载。以一简单的随机网络为例说明这个过程,令N=100,随机移除10个节点,负载变化如图1所示。以44号节点为例,网络结构发生变化后负载约为原始的1.597倍,倘若T小于这个数目,此节点过载失效,其余负载增大的节点同理,从而引发新一轮负载的变化。
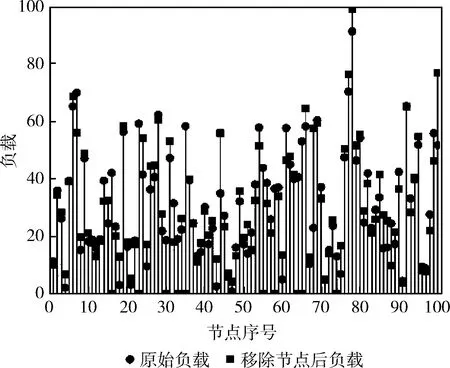
图1 随机网络中移除10个节点负载变化
2 基于级联失效的鲁棒性测度
网络性能常用抗毁性测度衡量,通常被定义为i个节点被移除后,其最大连通分量的规模的变化[5]。文献[11]考虑网络级联失效特点,采用级联失效前后,最大连通分量节点数之比衡量网络受损性能。本文结合级联失效改进网络鲁棒性测度。假使网络G中有n个节点,标号分别为1~n,则一个节点序列可表示为(k1,k2,…,kn),是节点的一个排序。按照节点排序K={k1,k2,…,kn}去逐个攻击网络G中的节点,当节点失效,执行上一节模型描述的级联失效过程。随着节点的失效,该网络在节点失效后的鲁棒性R可以定义为
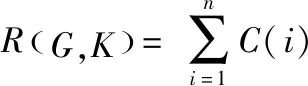
(4)
其中,C(i)表示网络G中i个节点遭到攻击,网络负载重分配完毕或级联失效过程完全完成后网络的最大连通分量规模。R(G,K)越小,随着节点失效下降得越快,说明网络在这些节点失效后越容易遭到破坏,节点越重要,识别方法越准确。
3 基于改进人工鱼群算法的关键节点识别
3.1 求解模型与基本人工鱼群算法
基于优化理论进行关键节点识别,目标是构造出节点失效后网络鲁棒性R(G,K)下降最严重的节点序列K,R(G,K)越小,说明当节点序列K失效时网络越容易崩溃。因此其构造方式可以视为一个优化问题[4,5]。表示如下

(5)
其中,Set_K是所有节点序列构成的集合。
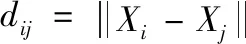
(1)觅食行为:人工鱼的感知距离范围Visual内随机选择一个新位置,向着对应适应度值更小的新位置移动。如果到达尝试次数后仍不满足前进条件,执行随机行为。
(2)聚群行为:聚群行为是指每条鱼在移动过程中趋向于相邻伙伴的中心以避免过度拥挤的行为。当前位置和中心位置对应适应度值Yi和Yc,nf为中心位置附近视野中的人工鱼的数量,δ为拥挤因子;Yc值更小且Yc/nf<δYi,则前进到中心位置。不满足条件则执行觅食行为。
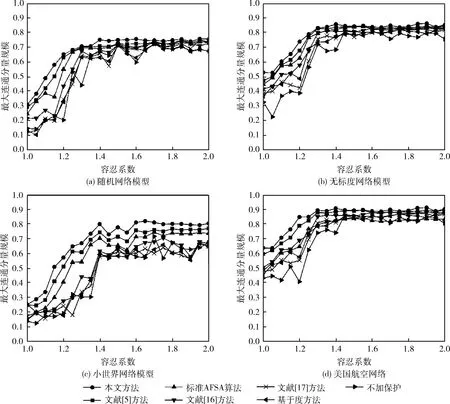
(3)追尾行为:追尾行为表示每条人工鱼在视觉范围内都朝着当前的最佳方向移动。假设Xmin是当前状态Xi的邻域内最优邻居。如果Ymin (4)随机行为:随机行为是在其视野中随机选择一个新状态Xnext,然后在该方向上移动一步。实际上这是默认行为。 (5)公告板:公告板用于记录鱼群中的最佳状态Xnext。 算法完成后,最终公告板的值是系统的最佳解决方案。 AFSA存在一些缺陷,例如更容易陷入局部最优值和缺乏多样性等。为了弥补这一不足,对AFSA进行改进。 (1)初始解的构造:本文通过引入佳点集的方法,优化AFSA算法的初始人工鱼群分布,提高AFSA算法的全局搜索性能。本质上,优化人工鱼群的初始分布是为了更科学地表征解空间的特征,人工鱼群体在解空间中的均匀分布是一种有效的策略,而随机产生的人工鱼群体在大多数情况下不能覆盖解空间的所有状况。由数论中的佳点集理论可知,佳点集的精度与空间维度无关,可以较好地适用于高维空间中的计算,同时,对于未知分布的对象,通过佳点集理论获得的佳点集Ps(i)的偏差远远优于通过随机方法获得的集合。因此,基于佳点集的特征,可以为群体智能算法中的群体分布提供更好的初始分布方案[14]。假设初始人工鱼群数为s,在n维空间中选择s点作为人工鱼位置,作佳点集 Ps(i)={({r1*i},{r2*i},…,{rn*i}),i=1,2,…,s} (6) r称为佳点,可由下式计算 (7) 其中,p为满足(p-n)/2≥n的最小质数,符号{a}表示数a的小数部分。由于本算法的解空间是节点序列的集合,将此佳点集映射到问题的可行域中,则第i个可行解的第k维的值为K(k,i)=[1+Ps(i)k(s-1)],i=1,2,…,s,符号[a]表示数a的整数部分。 (2)觅食行为的改进:在迭代过程中,标准AFSA算法通过觅食行为来实现全局搜索。当适应度值提高时,算法的收敛速度降低。细菌觅食优化算法(BFOA)中的趋化行为通过翻转与游泳操作使细菌聚集在一个更有利的环境中,能增强觅食行为,进入更大的搜索空间,并避免陷入局部最优状态。因此,采用BFOA算法的趋化行为对觅食行为进行改进[15]。与标准AFSA算法相比,趋化行为在处理觅食行为时增加了邻域搜索的频率和范围。适应度值在翻转操作完成后进行计算。当得到的适应度值更优,人工鱼将向该方向移动几步,直到游泳步数Ns达到极限值Nsmax或适应度值重合,否则执行随机行为。觅食行为在当前位置停止觅食,并翻转为另一条人工鱼,当所有人工鱼完成翻转,该过程完成。改进的觅食行为可以加快收敛速度并增加潜在解。人工鱼的位置i可以更新如下 (8) 其中,Step为实数。 (3)随机行为的改进:列维飞行是一种随机游走策略,是一种典型的飞行、跳跃的步长可进行变化的策略,从而使得搜索空间的结果更有效。因此,将列维飞行添加到自然启发算法中,可确保算法的改进。在AFSA中,随机行为是一种变异策略,可以防止算法陷入局部最优。在本节中,将列维飞行引入AFSA随机行为。列维飞行可简单近似为幂律行为,满足此分布的随机步长S可以通过Mantegna方法计算为 (9) 其中,u和v服从正态分布如下 u=N(0,σ2),v=N(0,1) (10) (11) (12) 为验证本文所提的关键节点识别方法的准确性,本节在3种不同拓扑结构的典型复杂网络及真实网络中进行仿真实验,包括本文所改进的优化算法与文献[5]中该领域已采用的优化算法、标准AFSA算法对比,及不同节点识别方法的对比。改进人工鱼群算法最大尝试次数50,最大迭代次数100,Nsmax取4,δ为0.618,人工鱼每次移动的最大步长step取1,visual取0.1。标准AFSA相同参数取相同值。整体关键节点识别方法与传统采用的基于度的衡量方法、文献[16]综合评价方法、文献[17]方法在不同网络结构上进行分析比较。3种典型网络的生成参照文献[18]。美国航空网络是研究负载变化的重要网络[8],本文用于实验的真实网络采用美国航空网络数据集[19]。复杂网络的建立及后续的实验均采用Matlab R2012a在Intel Core i7处理器配置下完成。 本小节主要探讨级联失效模型所涉及的关键参数T下保护不同方法识别的关键节点对网络抗毁性能的影响,具体关键节点识别方法的性能在后述小节进行对比,本小节不作详细叙述。采用不同方法在不同的容忍系数T下识别的节点序列中,保护前10%个节点,面对随机攻击的网络性能如图2所示。由网络级联失效模型可知,容忍系数T越大,则网络承载级联失效的能力越强。在4种网络中比较总体性能,当T不断增大,由级联失效引发的节点故障越少,网络性能都有所提高。不保护任何节点的网络性能曲线波动最大,基于优化算法的曲线性能值最高,曲线最平稳。这是由于不对任何节点进行保护,当随机打击的节点重要性较低,则对网络的影响较小,否则网络性能则受到较大影响,代表网络性能的鲁棒性值也就有所波动。使用优化算法识别关键节点过程中考虑了级联失效过程,保护对网络影响较大的关键节点,也相当于把引发较大级联失效的节点保护起来,每一个T下达到的性能最高。文献[17]方法虽然在仿真实验中考虑了级联失效动态特性,但关键节点识别仍是传统方法,与其它方法一样识别过程中不考虑级联失效的影响,而忽略一些会引发较大级联失效的关键节点,在随机打击下实验曲线有所波动,小世界网络中尤为明显。无标度网络各曲线起点值明显较高,对节点加以保护的各曲线均较为平稳,也说明了当无标度网络的少数关键节点保护起来以后,对随机失效有较强的抗毁性。美国航空网络的实验曲线变化与无标度网络类似,曲线起点值高且曲线平稳,面对随机失效具有较强的鲁棒性。 图2 不同容忍系数T下保护关键节点的网络性能比较 当T到达一定值,级联失效消失,而只有随机攻击引发的节点故障。以波动最大的小世界网络为例进行对比分析,基于优化算法和文献[16]综合评价方法的曲线在T达到一定值时趋于稳定,其它曲线波动较大,基于优化算法的曲线值仍然最高,说明基于优化算法的识别方法仍然比其它方法准确;其次为文献[16]的综合评价方法,当不考虑网络级联失效的特性,此种方法较为准确。文献[17]采用的评价指标实质计算上只涉及了度和介数两种指标,与基于度方法一样曲线值波动较大,说明保护关键节点后的网络性能得不到有效改善,识别的关键节点不太准确。对性能最好的本文方法,和采用的传统识别方法中性能最好的文献[16]方法进行详细分析,要达到稳定所需的T值,本文方法在随机网络中约为T=1.4,无标度网络中约为T=1.3,小世界网络中约为T=1.5,美国航空网络中约为T=1.3 达到的稳定值分别约为0.75,0.85,0.8,0.9;文献[16]方法对应T值分别为1.5,1.35,1.6,1.5,稳定值分别约为0.7,0.8,0.67,0.85,本文方法的网络性能分别优7.14%、6.25%、19.4%,5.88%;达到稳定值所需T值越小,亦即要排除级联失效影响需要对节点扩充的容量较小,节省成本,保护关键节点能有效改善网络性能。 将本文改进的AFSA算法与标准AFSA算法、文献[5]的禁忌搜索算法于4种网络中进行关键节点识别,本小节主要通过对比比较算法的优劣,验证本方法改进策略的有效性。在随机网络中选取T=1.3,无标度网络中选取T=1.2,小世界网络中选取T=1.4,美国航空网络中取T=1.2。在分析比较中,以第2节中鲁棒性函数R为目标函数进行搜索识别。由于所用于实验的网络及算法的目标函数是相同的,因而识别结果的差异主要受算法性能的影响。由图3可以看出,基于3种优化算法的识别结果有一定的相似度,在无标度网络中较为接近。在4种网络结构中基于改进人工鱼群算法的网络性能下降最快,移除相同数目的节点网络性能最低。其次为文献[5]方法。本文方法的结果优势是明显的,尤其是相较于标准AFSA算法而言。从优化算法寻优过程可知,各算法根据不同的节点序列排序使节点失效,依据适应度值最小判断出最优的序列,因此最后得到的节点序列应是失效后使网络性能值最低的序列,但优化算法不能遍历所有情况,因此需要不断寻求性能最佳的优化算法。本文算法在这个过程中寻找的序列最为准确,性能最好,这是由于AFSA算法相比于禁忌搜索算法而言具有并行处理能力,加之本文采用佳点集、趋化行为和列维飞行等改进策略,得到了较好的搜索效果。标准AFSA算法识别的关键节点失效对网络性能的影响比前两种算法弱,在搜索次数相同的情况下,标准AFSA算法还得不到较优的结果序列,作为相比于禁忌搜索算法本具有的优势也没有体现出来,也说明了本文改进策略的有效性。 图3 移除不同优化算法识别的关键节点后网络性能比较 为分析整体关键节点识别方法性能,采用移除排序靠前节点来分析网络性能的变化。如图4所示,由网络性能的变化可以看出本文方法的前10%至20%左右的节点移除后,网络连通性急剧下降,网络效率下降明显,3种典型拓扑结构网络中,随机网络模型中移除27%节点,无标度网络中移除17%节点,小世界网络中移除36%的节点,网络性能即降低到0.1以下,其次为文献[16]方法,使网络性能即降低到0.1以下需分别移除41%、32%、52%节点,说明本文算法较为优越。以无标度网络为例列出各方法得到的节点序列前10%的结果见表1,可以看出本文方法与其它方法识别结果差异较大。由于本文利用优化算法进行关键节点识别的过程中考虑了级联失效的影响,所识别的引发较大级联失效的几个节点,在其它方法序列前10%节点中基本都不含有,当这些重要节点被攻击,同时引发级联失效以最大化地破坏网络,网络性能急剧下降,其它3种传统关键节点识别方法则没有考虑网络的这种动态特性。3种传统方法中网络性能下降最快的是文献[16]方法,在随机网络和小世界网络中较为明显,在无标度网络中3种传统方法效果差别不大。这是由于文献[16]方法考虑的多个指标中包括网络的整体连通性,更为全面,另两种方法评价节点重要性时则没有考虑。无标度网络少数关键节点往往也是度最大的节点,由表1可看出,3种方法识别的节点较为接近。 图4 移除不同方法识别的关键节点后网络性能比较 表1 各方法对无标度网络的节点识别排序部分结果 在美国航空网络的实验中,本文方法仍取得最优的结果,使网络性能降低至0.1以下,本文方法、文献[16]、文献[17]、基于度方法识别的关键节点需分别移除36%,57%,66%,71%的节点,对网络造成崩溃,对关键节点的攻击强度本文比其它方法分别要低36.8%,45.5%,49.3%,本文方法最为优越,对关键节点识别也最为准确。综合上述分析,本文方法考虑网络级联效应影响进行关键节点识别,较其它传统不考虑级联效应影响的方法更为准确,更为贴合网络实际情况,本文的关键节点识别方法在不同拓扑结构网络中均具有较高的准确性,能较好地适用,本文改进人工鱼群算法的策略也有效地提高了算法的性能。 如何更准确地寻找网络关键节点,对提高网络稳定性,预防网络大规模故障至关重要。本文一方面引入网络级联失效模型,在分析网络性能时,考虑节点级联失效以贴近网络的实际情况;另一方面改进人工鱼群算法,使得采用优化理论进行关键节点识别时更为高效准确。通过在不同类型拓扑结构网络与实际网络上进行实验与分析,验证了本文关键节点识别方法的有效性和优越性。3.2 算法性能改进
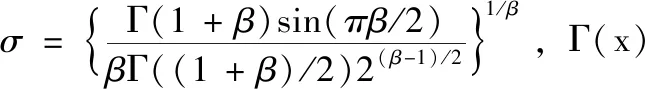
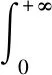
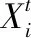
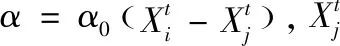
4 实验仿真与分析
4.1 不同容忍系数下保护关键节点的网络性能比较
4.2 改进优化算法性能分析

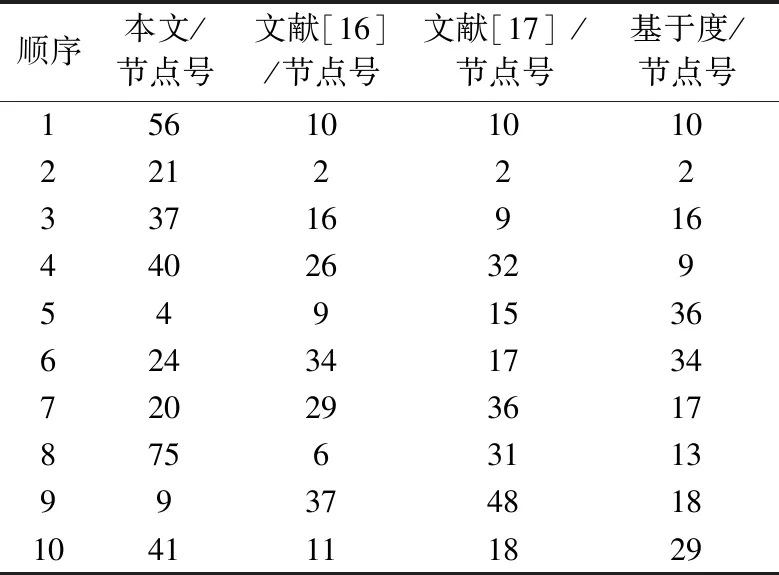
4.3 整体识别算法性能分析
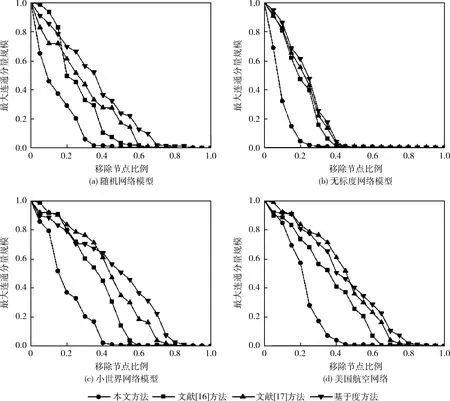
5 结束语
