风力机齿轮箱振动信号分解方法研究
2021-04-22叶柯华
胡 璇, 李 春,2, 叶柯华
(1.上海理工大学 能源与动力工程学院,上海 200093; 2.上海市动力工程多相流动与传热重点实验室,上海 200093)
随着风力机趋于大型化发展,其传动系统也越来越复杂,同时其服役环境具有显著的非定常性,风力机齿轮箱时刻处于非平稳交变载荷作用下。受多样传递路径和调制作用等影响,其振动信号具有明显的非线性和非平稳性。因此,在强噪声背景中提取风力机齿轮箱的振动信号特征是故障诊断的重点和难点[1-3]。
信号分解为故障诊断重要的预处理过程,为剔除冗余及构建故障特征向量提供基础信息。目前,常见的分解方法有集合经验模态分解(EEMD)、固有时间尺度分解(ITD)及经验小波变换(EWT)分解等[4-6]。胡茑庆等[7]利用经验模态分解(EMD)对齿轮箱振动信号进行分解,辅以峭度重构信号,实现信号特征的有效提取。Gaci[8]提出基于EEMD分解的新去噪技术,并与离散小波变换进行比较以获得良好的降噪效果。Park等[9]对齿轮箱传动故障信号进行EEMD分解,提取本征模态函数(IMF)分量的波峰系数和形状系数作为故障特征,结合k值临近算法对故障进行分类。Xing等[10]将齿轮振动信号通过ITD分解为若干相互独立的固有旋转(PR)分量,结合奇异值分解以提高复杂工况下信号特征提取的鲁棒性。Feng等[11]基于振幅和频率解调方法,采用ITD用于齿轮箱故障诊断,并将所得振幅和频率解调频谱与理论齿轮故障特征频率进行匹配,以此识别故障类型。Chen等[12]利用EWT对风力机振动信号进行自适应分割,并构造小波滤波器提取调幅-调频函数,在归一化处理后,通过概率神经网络达到90%的诊断准确率。Chemseddine等[13]结合Hilbert变换和EWT分解信号以获得瞬时振幅矩阵,然后利用奇异值分解和Elman神经网络实现状态识别和分类。
EEMD对非线性、非平稳信号具有良好的自适应频带分割能力,但其作为递归模态分解,存在端点效应及分解误差受采样频率影响显著的问题[14]。ITD能够克服传统瞬时频率计算方法造成的边缘效应和负频率等现象,但是信号分解后易出现失真[15]。EWT可以较好地解决模态混叠及虚假分量等问题,但对复杂振动信号分解易丢失边频带信息[16]。
针对风力机齿轮箱振动响应显著的非线性和非平稳性特征,笔者分别采用以上3种方法对振动信号进行分解,然后提取分解信息熵以构建故障特征向量,并输入支持向量机(SVM)进行识别和分类,最后通过比较各信号分解SVM诊断准确率,分析各方法的效果。
1 风力机齿轮箱振动信号
本文振动信号数据来自美国国家可再生能源实验室(NREL)“Gearbox Reliability Collaborative(GRC)”项目测试采集的正常和故障风力机齿轮箱加速度振动信号[17]。箱体结构如图1所示,由1级行星轮系和2级定轴轮系构成。齿轮箱具体参数见表1,其中L、R分别表示左旋和右旋。
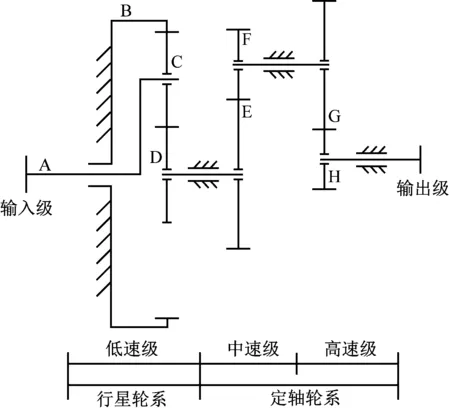
A-行星架;B-内齿圈;C-行星轮;D-太阳轮;E-中速级主动轮;F-中速级从动轮;G-高速级主动轮;H-高速级从动轮。
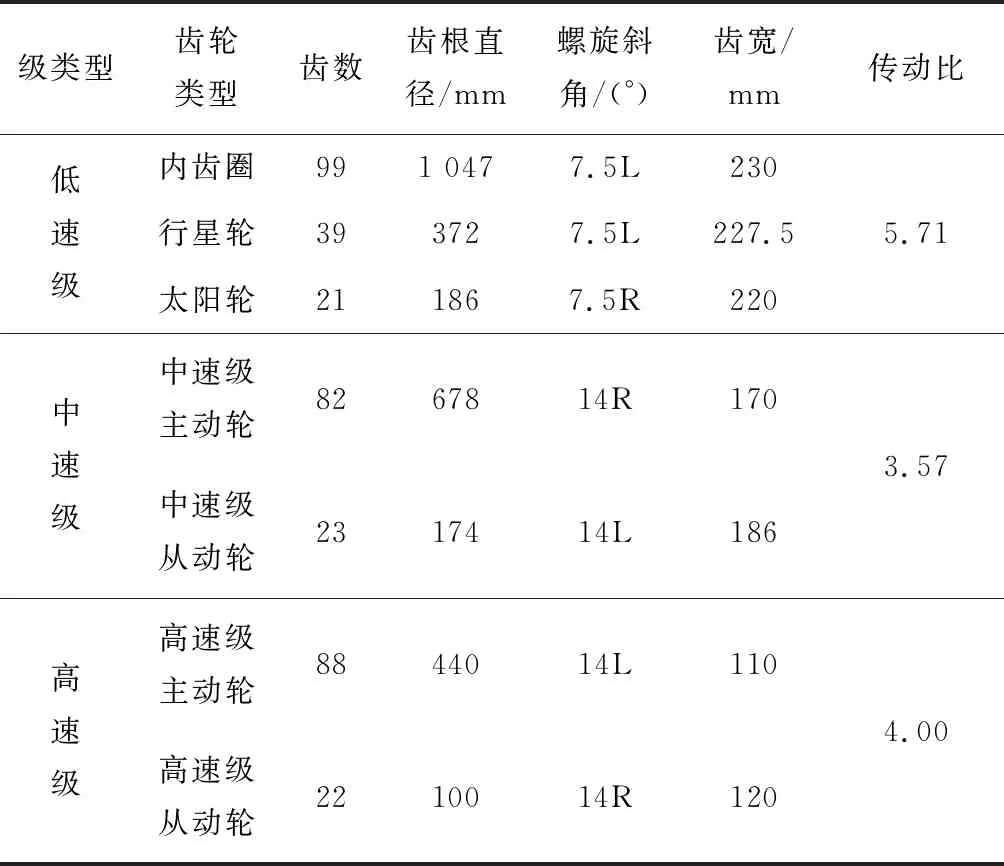
表1 齿轮箱参数
测试样机安装于NREL试验风场内,其齿轮箱在运行期间发生油损事故,之后NREL将其拆卸,并在实验室环境下分别采集其正常和故障状态下振动信号加速度数据。齿轮箱内共布置8个加速度传感器(AN1~AN8),位置分布如图2所示。
由图2可知,AN8传感器位于损坏齿轮附近,振动较为强烈,信号所含信息更为丰富。故采用该传感器收集振动数据,采样频率为40 kHz。
图3为齿轮正常和故障状态下的加速度振动信号。由图3可知,振动信号时域波动呈混乱无序状态,无法人为地直观判断齿轮健康状态。故需对齿轮箱振动信号进行分解并作进一步处理,具体流程如图4所示。
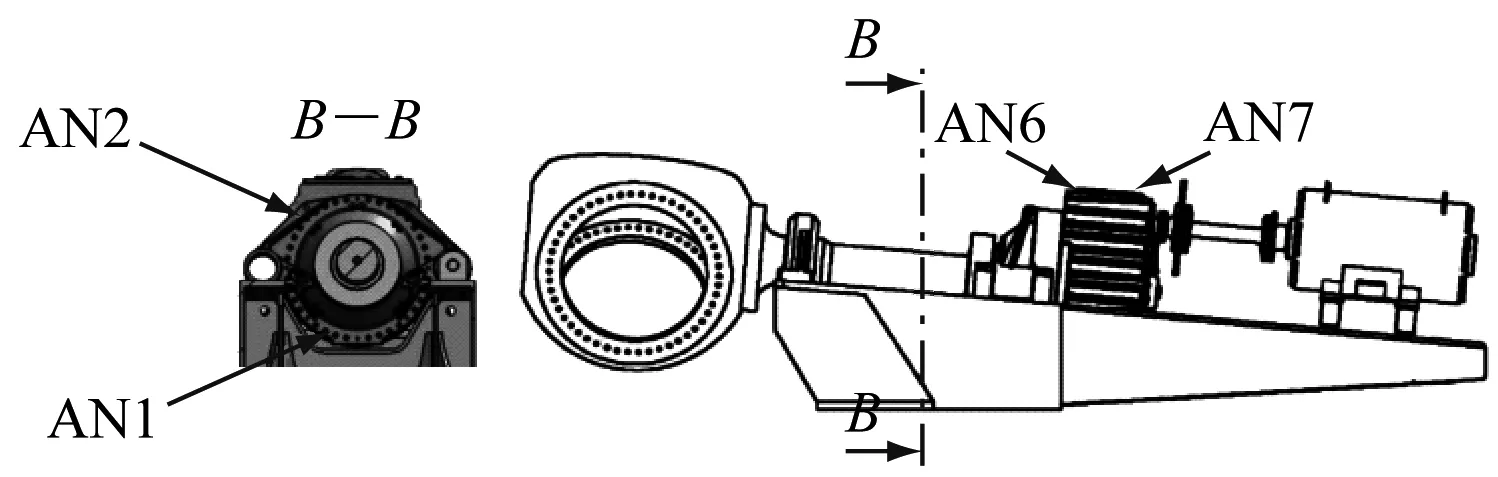
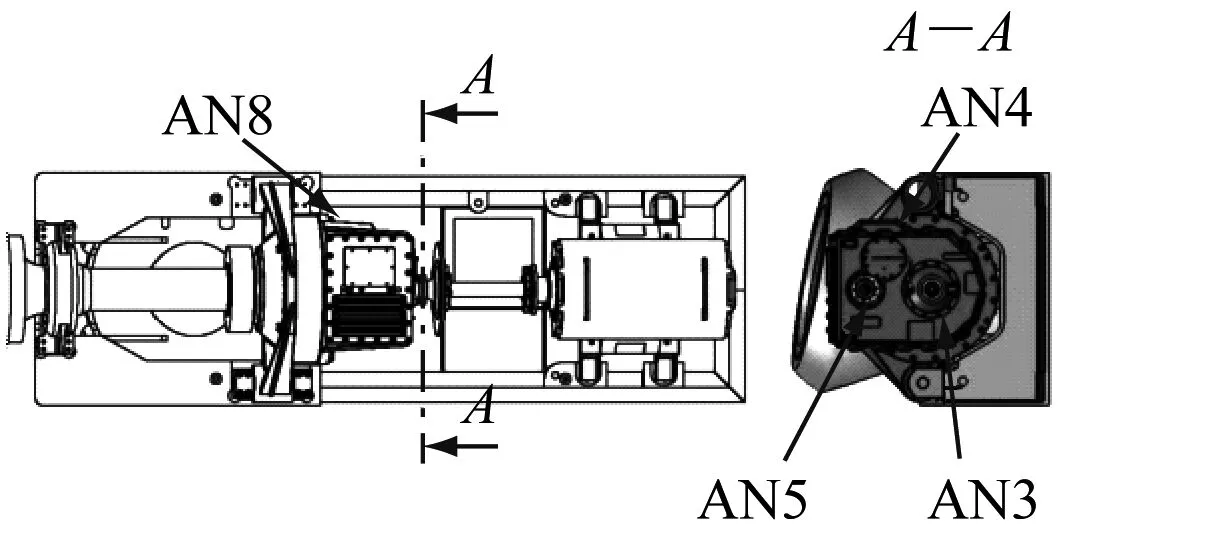
图2 振动传感器位置
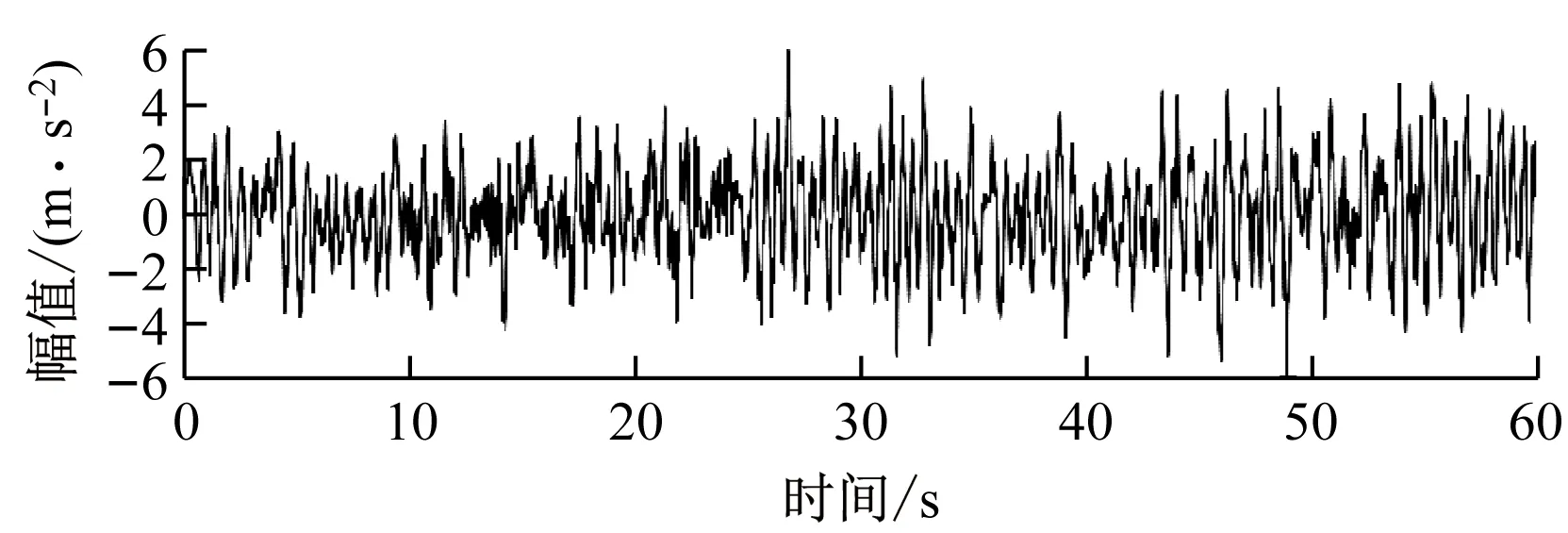
(a) 正常状态
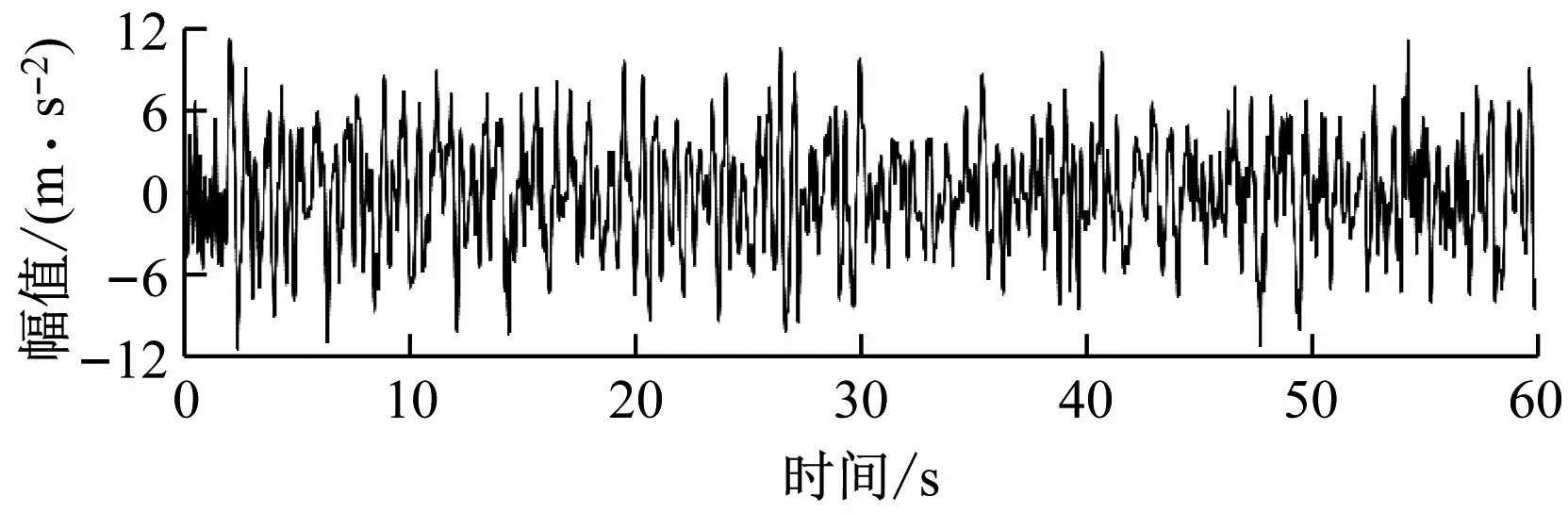
(b) 故障状态
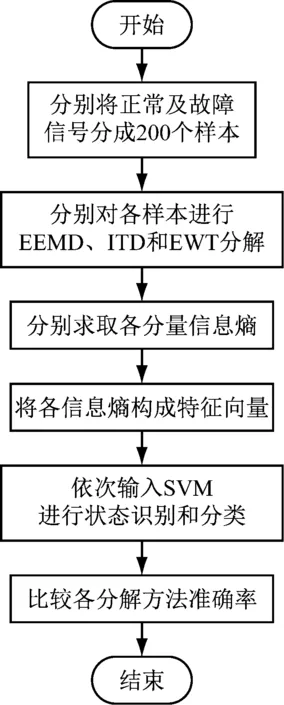
图4 故障诊断流程图
2 信号分解方法
2.1 EEMD分解
EEMD是由Wu等[4]于2009年在经验模态分解的基础上提出的一种自适应时频分析方法,根据信号局部特征时间尺度将其分解为多个IMF分量。齿轮箱振动信号的EEMD分解结果如图5所示。
由图5可知,齿轮箱正常状态下振动信号经EEMD分解成9个IMF分量和1个残差分量,且前6个IMF分量包括了样本绝大多数信息;故障状态下振动信号经EEMD分解得到8个IMF分量和1个残差分量,前5个IMF分量包含样本多数信息。
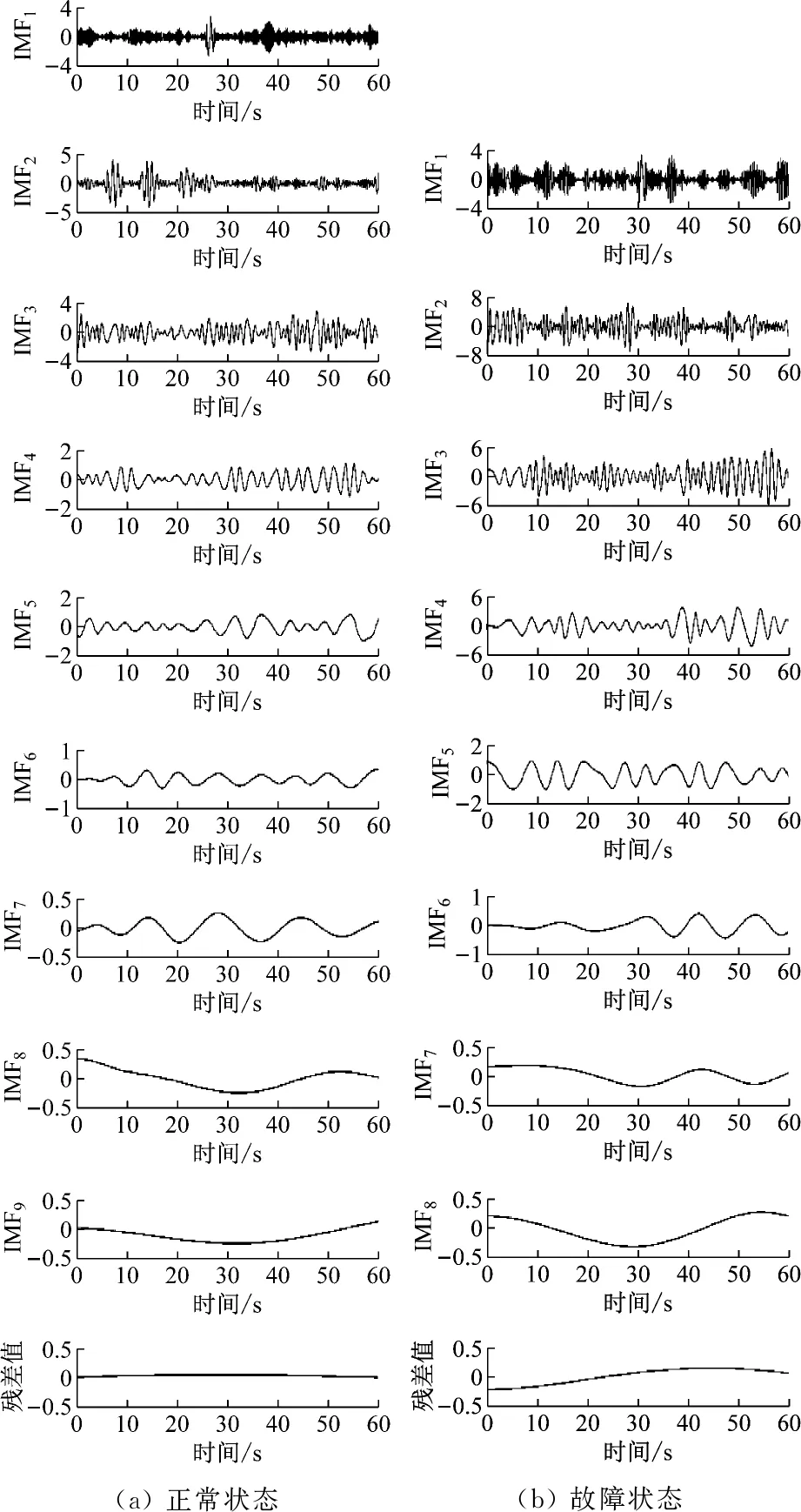
图5 EEMD分解结果
2.2 ITD分解
ITD是一种自适应时频分析方法[5],其根据信号本身局部时间尺度特性,基于线性变换原理构造基函数,将信号自适应地分解成若干PR分量和一个趋势分量。振动样本信号进行ITD分解,结果如图6所示。
由图6可知,正常和故障状态下振动信号经ITD分解均得到3个PR分量和1个残差分量,各分量包含样本信号的大多数信息。
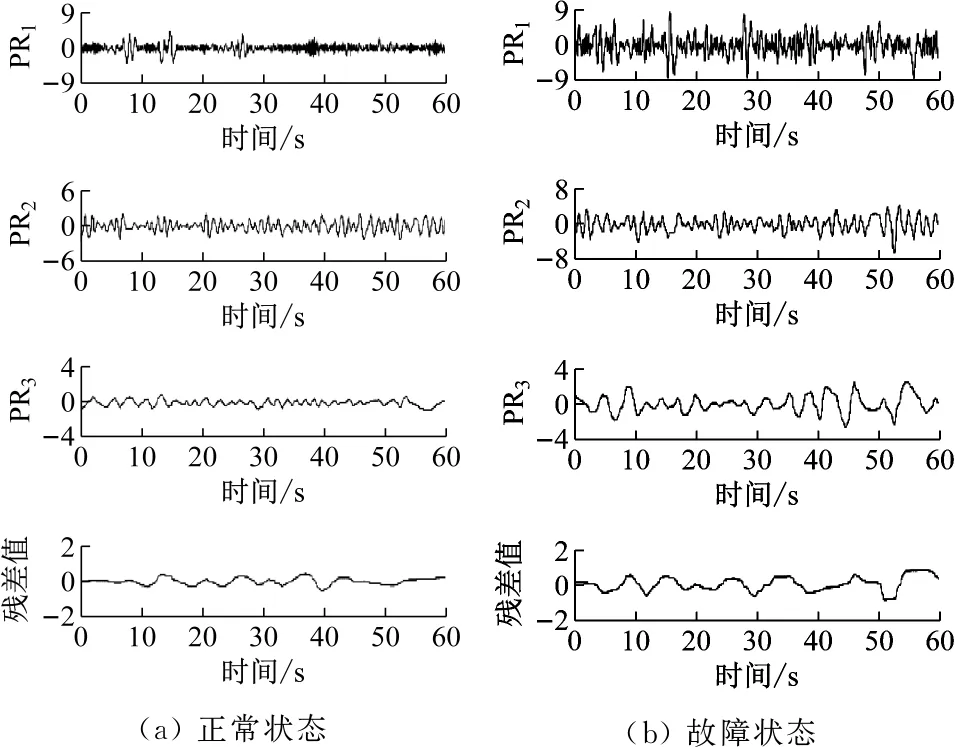
图6 ITD分解结果时域图
2.3 EWT分解
EWT是由Gilles于2013年提出的一种自适应信号处理方法[6]。其核心思想是通过对信号傅里叶谱进行自适应分割,从而建立合适的带通滤波器以提取信号不同的调频调幅成分。齿轮箱振动样本信号经EWT分解后的结果如图7所示。由图7可知,正常和故障状态下信号进行EWT分解后得到5组经验模态分量。
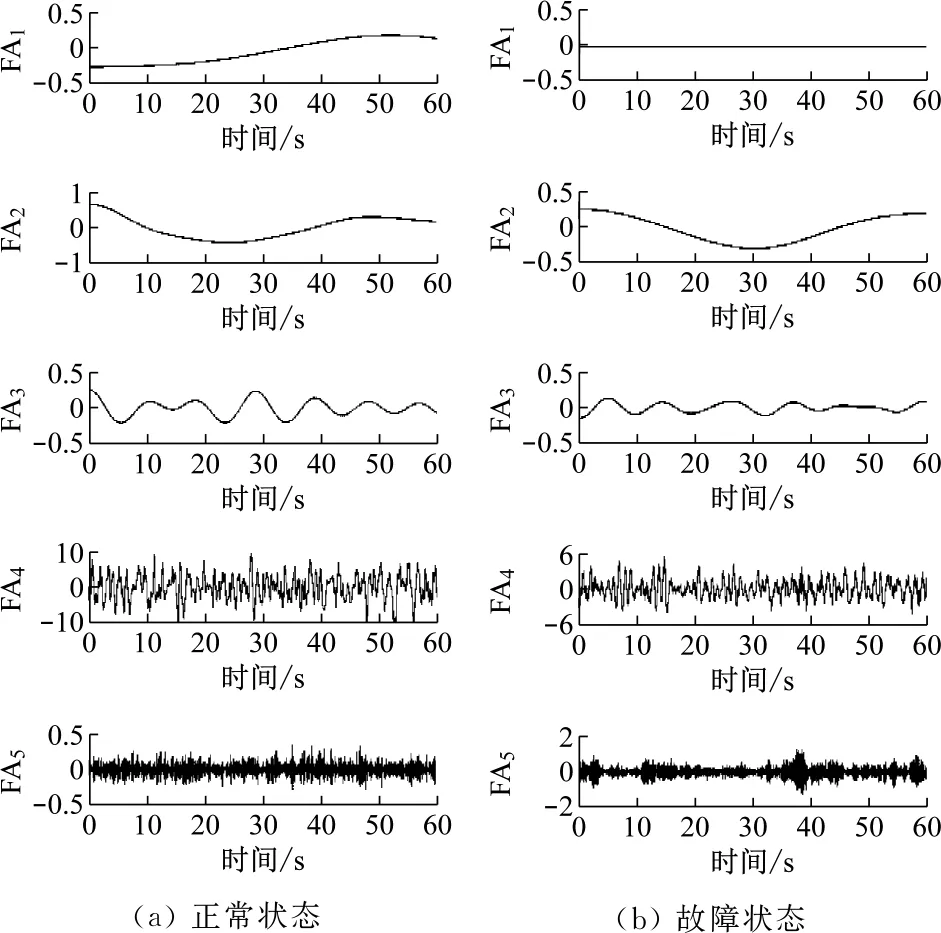
图7 EWT分解结果
3 信号特征提取
3.1 峭度
峭度为无量纲参数,是信号归一化4阶中心距,以量化时间序列非高斯性。其对信号冲击成分高度敏感,故常在工程应用中作为故障诊断的依据[18]。
峭度的计算公式为:
K=E(x-μ)4/σ4
(1)
式中:K为峭度;x为信号值;E为数学期望;μ为振动信号的均值;σ为振动信号的标准差。
正常状态下,振动信号的峭度值约为3,且随着故障程度的加深,冲击成分增多,峭度指标逐渐提高[19]。表2为一样本信号故障和正常状态下,经不同分解方法所得分量的峭度值。
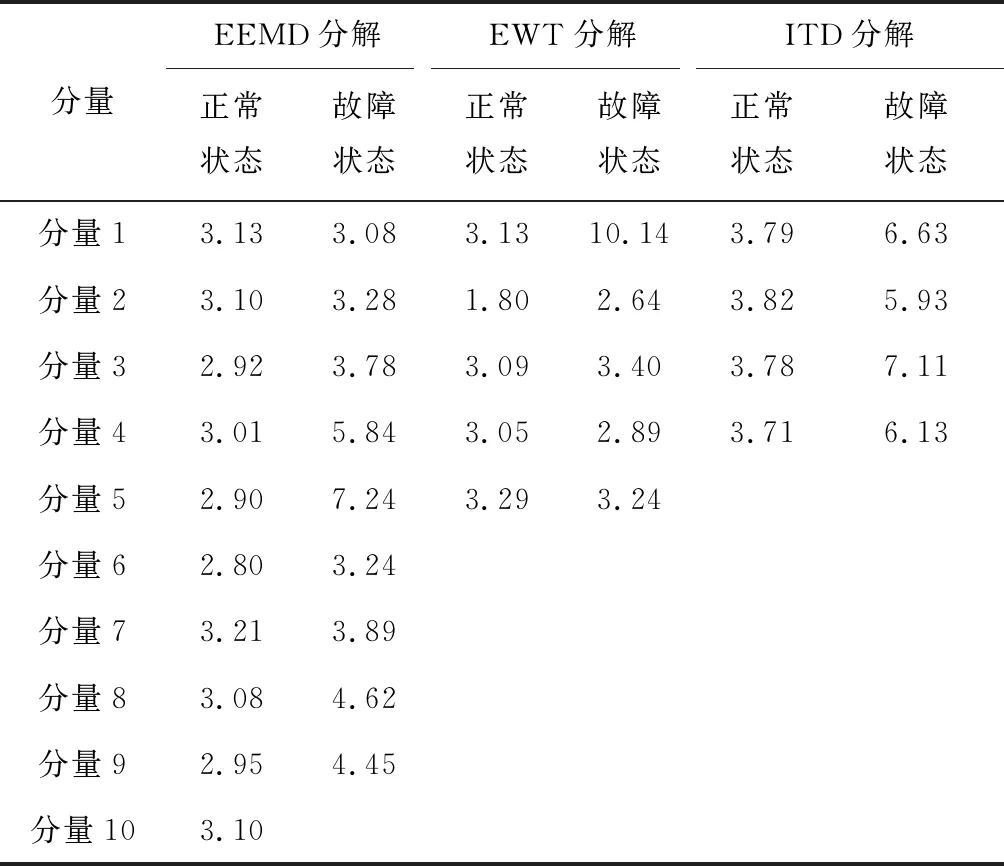
表2 各类峭度值结果
由表2可知,各分解方法分量的正常状态峭度值大多小于故障状态峭度值。且正常和故障状态信号经EEMD和EWT分解后,其大部分分量峭度值差距不大,约为3,无法通过峭度值大小来直观判断故障发生与否。而ITD分解后分量在不同状态下的峭度值出现明显差异,其正常状态下峭度值约为3,故障状态下峭度值范围为5~8。EEMD分解差异主要体现在分量4和分量5,冲击成分大多分布在分量4和分量5;EWT分解冲击成分主要分布在分量1和分量3;而ITD分解的冲击成分均匀分布在各个分量。
3.2 信息熵
设随机序列x(n)={x1,x2,…,xn}中包含N个可能值,且分布概率为P={p1,p2,…,pn},则序列信息熵H(x)为:
(2)
信息熵是用来描述系统有序性的物理量,与系统内在规律程度呈负相关。且概率分布越接近,信息熵值就越大,可以将其作为样本序列的不平稳性量化指标[20]。因此,选取信号分解后信息熵较小的分量作为支持向量机输入量可以提高其分类精度。
由于样本数量较多,故随机选取各分解方法不同状态下的一个分量信息熵,具体数据如表3所示。
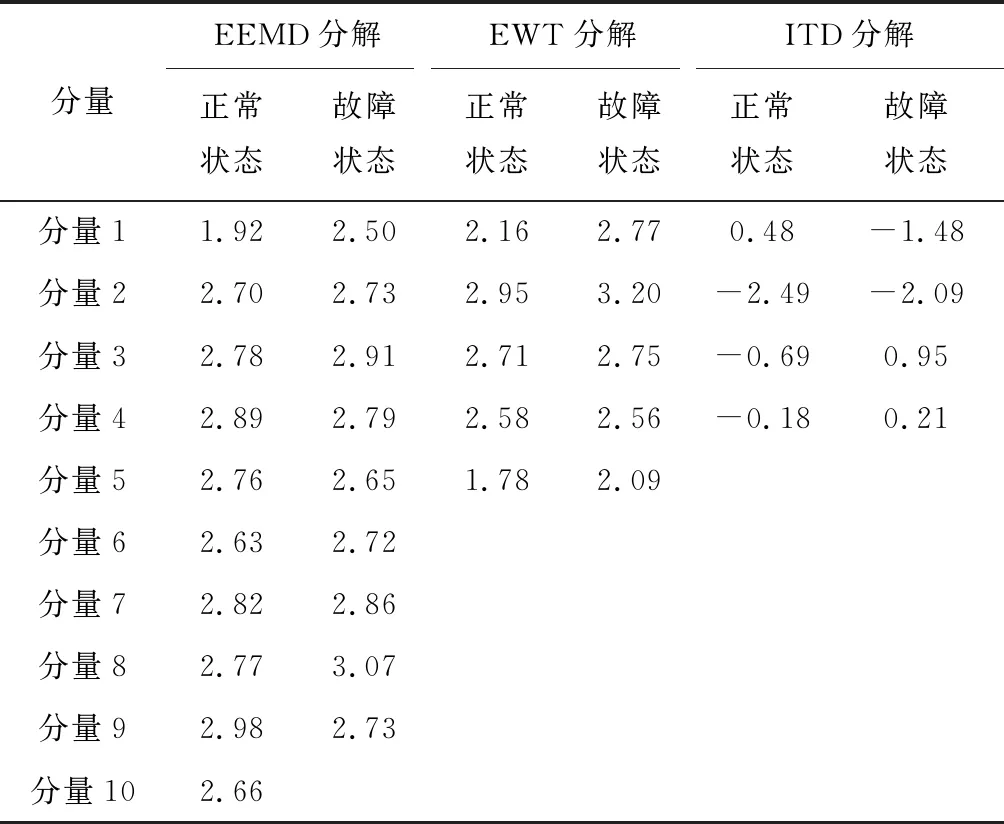
表3 各类信息熵结果
由表3可知,各分解方法分量正常状态下的信息熵大多小于故障状态下的信息熵。且EEMD分解分量随序号增大,其信息熵整体呈增大趋势,可见序列越靠前分量越平稳有序。而EWT分量的信息熵则随序号增大呈下降趋势,可判定其序号较大分量更平稳。ITD分量的信息熵并没有显著递增或递减趋势。不同分解方法的信息熵特征不同,表明各分解方法的分解原理不同。将各样本信息熵构成特征向量作为SVM输入参数进行状态识别和分类。
4 信号识别与分类
分别计算各分解方法所得样本分量的信息熵Suv,其中u为信号样本序号,v为分量序号;T为800个样本各分量的信息熵向量集。
Su=[su1su2…suv]
(3)
T=[S1S2…S800]
(4)
采用SVM方法进行故障识别时,故障和正常样本各占训练样本总数的50%,另选其他若干样本为测试样本。
为求证不同分解方法的优异性,分别将各分解方法得到的样本信息熵特征集SVM分类结果进行比较。图8和图9分别为测试样本数为100和200时,EEMD、ITD和EWT进行SVM分类的诊断结果。
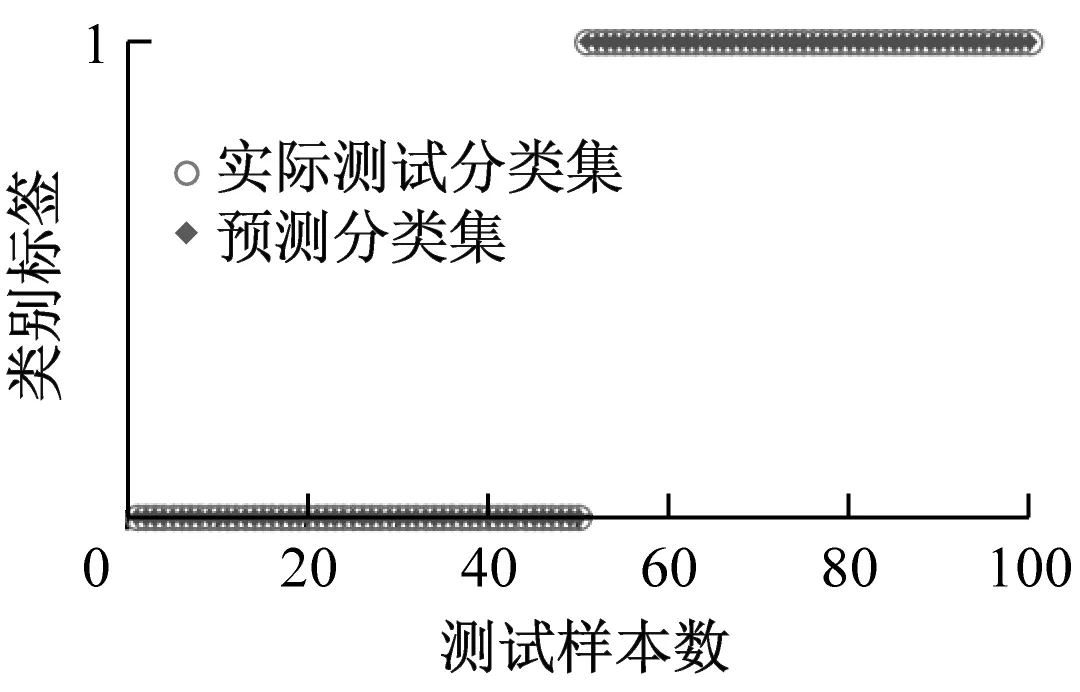
(a) EEMD
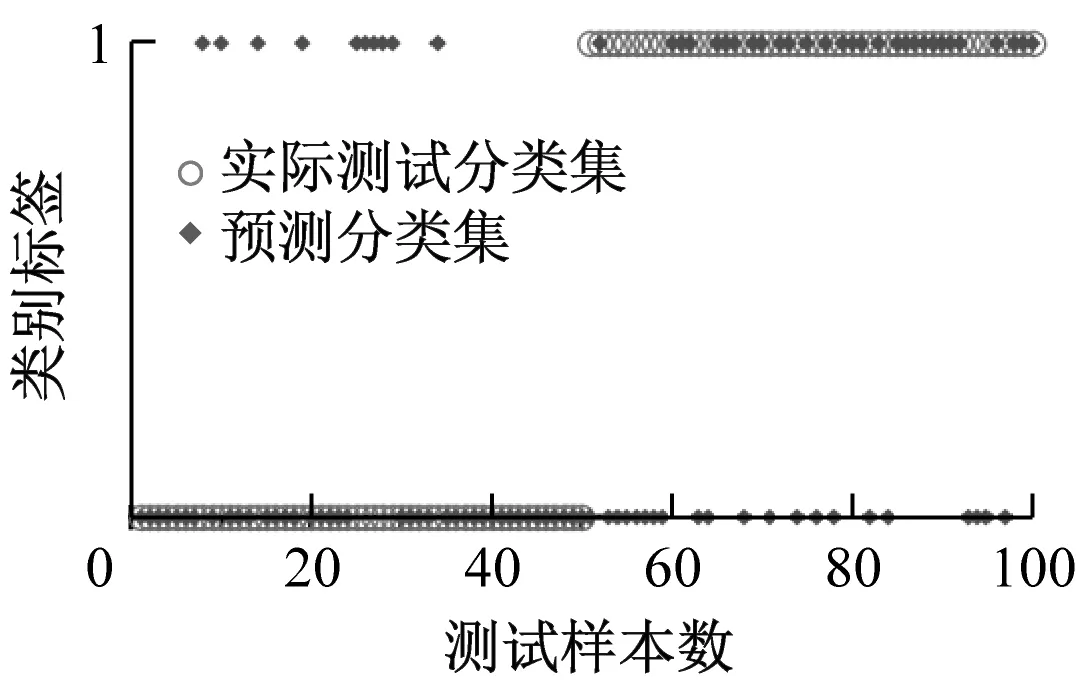
(b) EWT
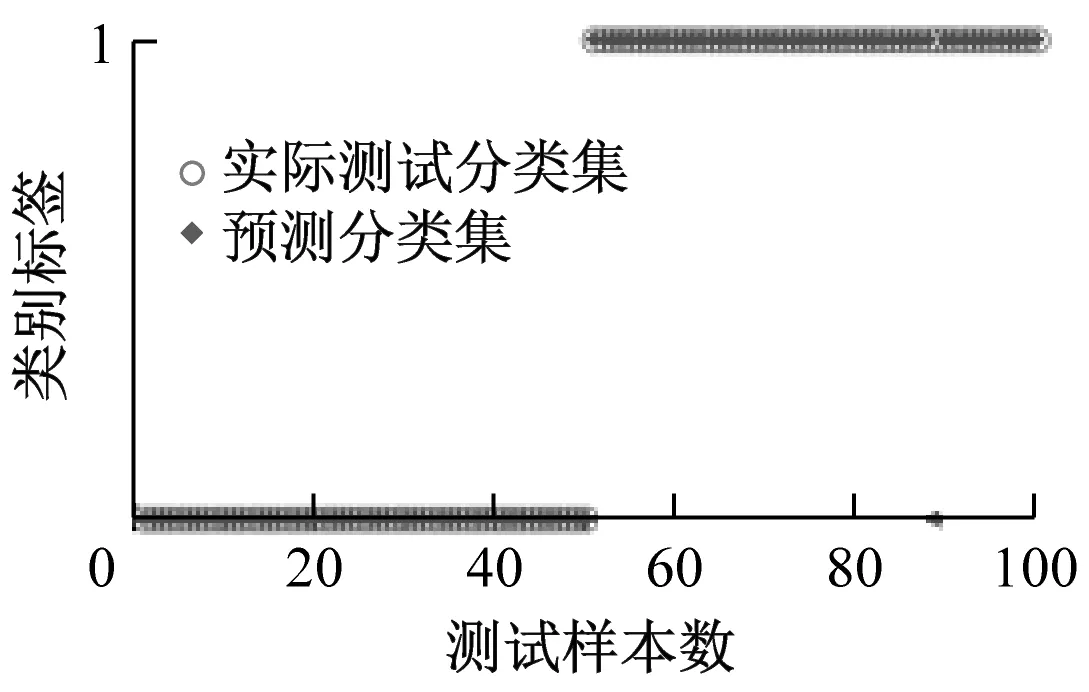
(c) ITD
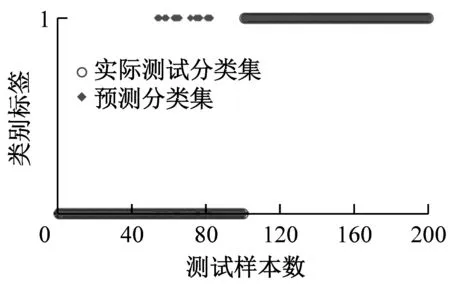
(a) EEMD

(b) EWT
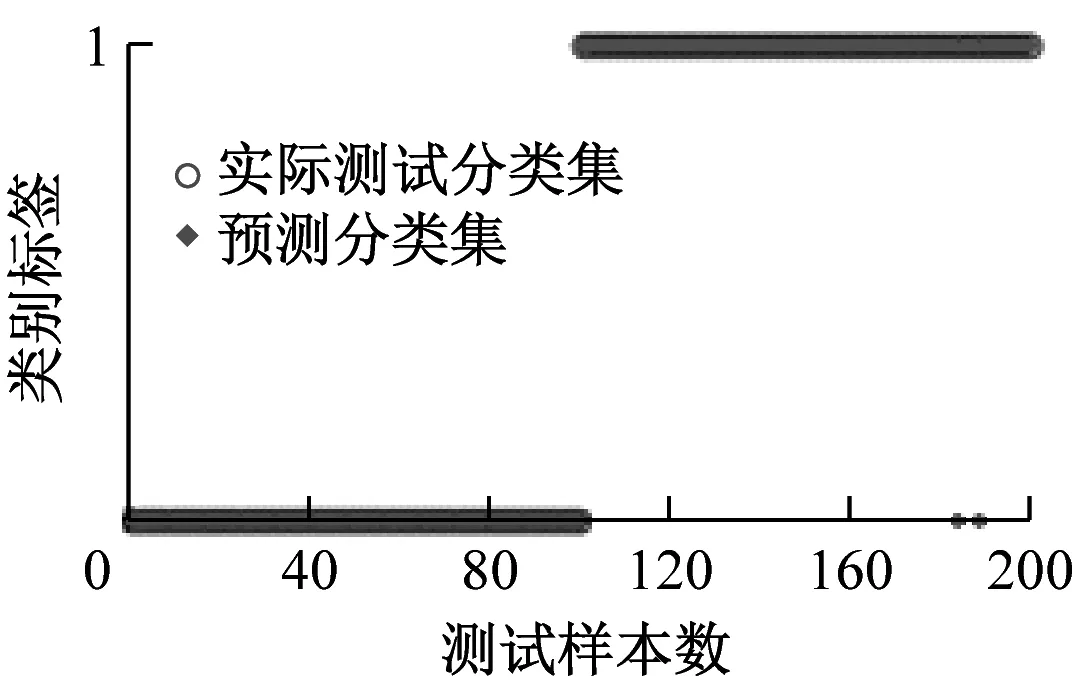
(c) ITD
表4给出了测试样本数为100、200和300时,各分解方法所得信息熵故障识别的准确率。由表4可知,EWT分解方法所得信息熵作为SVM模型输入参数时,在不同测试样本数下的诊断准确率最低,测试样本数为300时准确率只有67.0%,平均准确率仅68.3%。EEMD分解方法所得信息熵作为输入参数时的准确率相比EWT要高,测试样本数为100、200和300时的准确率依次为100.0%、92.5%和93.7%,平均准确率为95.4%;ITD分解方法所得信息熵作为输入参数时平均准确率为99.2%,测试样本数为100、200和300时,准确率依次为99.0%、99.5%和99.0%。由以上分析可知,ITD在3种分解方法中的诊断准确率最高且最稳定。
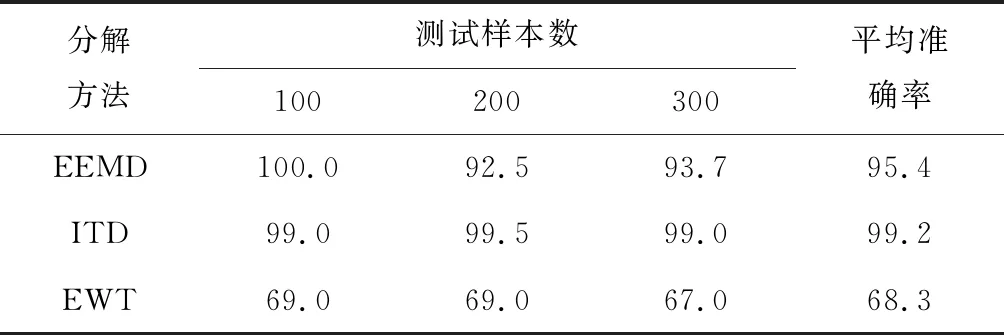
表4 各分解方法的准确率计算结果
5 结 论
(1) 对于含有冲击成分的振动信号,EWT分解冲击成分主要体现在分量1和分量3;EEMD分解后冲击成分主要集中在分量4和分量5;而ITD分解后冲击成分较均匀,分布于各分量,不能很好地提取信号冲击成分。
(2) 不同信号分解方法所得分量的信息熵分布不同,各分解方法获得分量在正常状态下的信息熵均小于故障状态下的信息熵,说明信息熵值越小该序列越稳定。EEMD分解后序列越靠前分量越稳定;EWT分解序列越靠后分量更有序;而ITD分解无明显分布规律。
(3) 3种不同分解方法中,EWT分解方法的平均准确率最低,仅为68.3%,无法有效分解齿轮箱振动信号。而ITD分解方法准确率最高,且在不同测试样本数下表现最稳定,故ITD最适用于风力机齿轮箱信号分解。
