椭圆管束层流尾迹的流动过渡和分岔
2021-04-22李易蓉
李易蓉, 杨 茉, 张 政
(上海理工大学 能源与动力工程学院,上海 200093)
横掠管束在工业上有广泛应用[1-4],因此强化横掠管束的对流换热具有很高的工程应用价值。研究表明[5-7],相对于传统的圆管,椭圆管的迎风面积和管后回流区更小,管外压降和阻力较小,且由于椭圆管的当量直径较小,更有利于换热。因此,关于椭圆管换热器的研究日益受到重视[8-9],但目前的研究方向集中于对比圆管与椭圆管的换热情况,对椭圆管流动换热规律的研究较少。
针对横掠单管后方尾迹发生周期涡脱落的现象,Sau等[10-12]发现这是由于雷诺数Re增大至临界值,超临界Hopf分岔的发生使尾迹进入周期振荡状态。多个管子竖直排列时,在自身发生绕流脱体的同时,尾涡还会发生相对作用,涡脱落的情况会更加复杂。针对2个竖直对称排列的圆管,Xu等[13]通过实验方法发现在改变雷诺数和无量纲管间距的情况下,尾迹中存在非对称的流动状态,这种流动状态表现为流动的偏离[14]。Mizushima等[15-16]证明管束后方尾迹的流动偏离使得尾迹从周期振荡进入不稳定振荡(准周期)状态。Peng等[17]发现无量纲管间距较小时,随着雷诺数的继续增大,间隙流动从稳定偏离快速过渡到不稳定偏离,加剧了尾迹之间的相互作用,系统从准周期状态进入混沌状态。随着无量纲管间距的进一步增大,Kang等[18-19]对2个竖直排列的圆管进行尾迹分析时发现,在低雷诺数下尾迹从同相同步流动过渡到反相同步流动;Peng等[20]通过数值模拟和分岔分析,发现在2个竖直排列椭圆管涡脱落过程中,尾迹中同时存在同相和反相流动。Alam等[21]对空气横掠4个竖直排列的圆管进行数值模拟,发现无量纲管间距为0~2.0时会出现同相同步流动到反向同步流动的过渡。
目前,还没有关于超过2个竖直排列的椭圆管尾迹流动状态的研究。因此,笔者对低雷诺数下空气横掠4个竖直排列的椭圆管进行二维数值模拟,并分析了其在不同无量纲管间距下的流动非线性特性,为进一步研究流动换热规律奠定基础。
1 物理模型及数学描述
1.1 物理模型
如图1所示,入口到椭圆管中心的距离为X1,椭圆管中心到出口的距离为X2,计算域的高度为H[18]。4个椭圆管等间距竖直排列,2个椭圆管之间的无量纲管间距为G=L/b(b为椭圆管短轴长度,L为2个椭圆管切点之间的距离),选取3个监测点(监测点8~监测点10),具体参数取值见表1,其中D为与椭圆管具有相同周长的圆管直径,a为
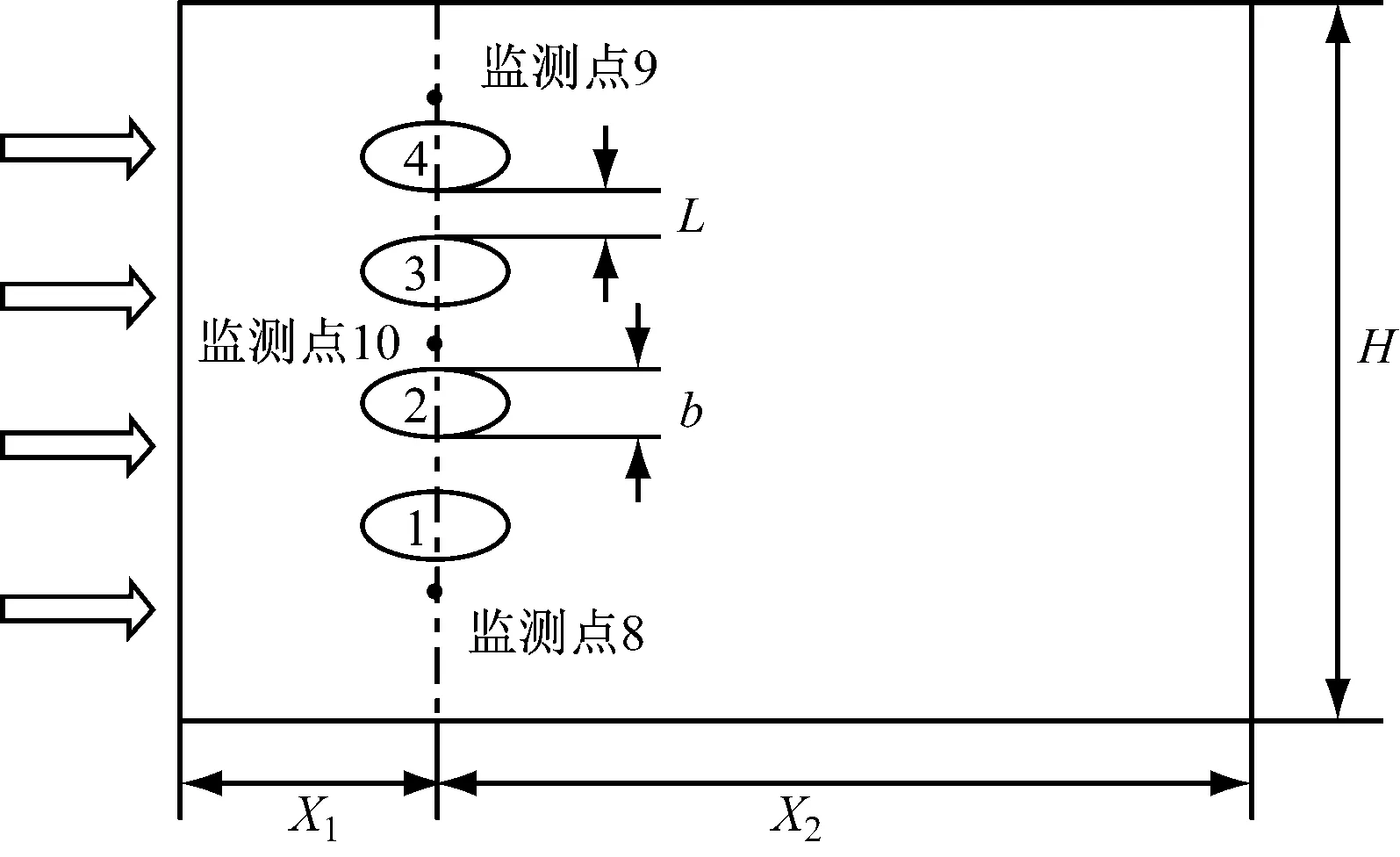
图1 计算域

Tab.1 Parameters of computational domain and the elliptical tube
椭圆管长轴长度。
空气以恒定来流速度Ul和温度T∞从左侧入口流入,管壁采用速度无滑移条件,同时保持椭圆管壁温度Tw恒定,上下壁面为对称边界条件,空气从计算域的右侧出口流出,出口设置自由出流条件。
1.2 数学模型
假设工作介质(烟气)是常物性,不可压缩的空气(普朗特数Pr=0.7)的动力黏度为常数。流动是二维的,定义无量纲参数:X=x/D,Y=y/D,U=u/Ul,V=v/Ul,τ=t/(UlD),P=p/(ρUl),Θ=(T-T∞)/(Tw-T∞),Re=UlD/υ,Pr=v/α。其中,u、v分别为笛卡尔坐标系中x和y方向的速度分量;p为压力;T为温度;υ、α分别为运动黏度和热扩散系数;t为时间;ρ为密度。
无量纲连续方程为:
(1)
无量纲动量方程为:
(2)
(3)
无量纲能量方程为:
(4)
入口边界条件为U=1,V=0,Θ=0 ;出口边界条件为∂U/∂X=0,∂V/∂X=0,∂Θ/∂X=0;上下边界条件为∂U/∂Y=0,V=0,∂Θ/∂Y=0;管壁边界条件为U=V=0,Θ=1。
1.3 钝体绕流的相关参数
钝体绕流的相关参数主要包括升力系数CL、阻力系数CD以及斯特劳哈尔数St,定义如下:
(5)
(6)
St=fb/U
(7)
式中:FD和FL分别为时均阻力和时均升力;U∞为流体绕流钝体的自由来流速度;f为涡脱落的频率。
2 网格独立性和计算方法验证
基于Fluent软件采用直接模拟(DNS)对空气横掠椭圆管束模型进行求解。通过有限容积法离散N-S控制方程,将计算域分成多个小的控制体,对每个控制体的变量进行积分,将所有区域看成整体进行耦合计算。采用QUICK格式对控制方程的对流项进行离散,采用SIMPLE算法对速度和压力进行耦合求解。当Re=100、无量纲管间距G=2.0时,对流体横掠椭圆管束进行模拟计算。表2给出了在不同的网格划分情况下(d为正方形网格边长,Nn为网格数)椭圆管1的平均阻力系数CD1、平均升力系数CL1、斯特劳哈尔数St1和平均努塞尔数Nu1。当d为1.5 mm、网格数为62 450时,CD1和St1不再变化,其余参数的最大偏差不超过0.09%。

表2 网格无关性验证
由图2可知,当时间步长为0.005和0.001时,椭圆管1的斯特劳哈尔数St1的变化情况基本一致,可以保证结果的准确性,为减少计算时间,最终选择时间步长为0.005。
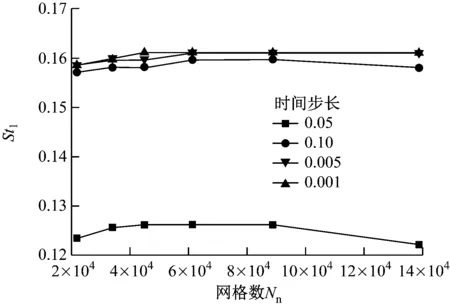
图2 不同时间步长下椭圆管1的斯特劳哈尔数St1的变化
3 模拟结果
表3给出了低雷诺数下无量纲管间距G为0.5、1.5、2.0、3.0和3.5时横掠椭圆管束的模拟结果。其中,V10为监测点10在Y方向的时均速度,CL,t为椭圆管束总的时均升力系数。
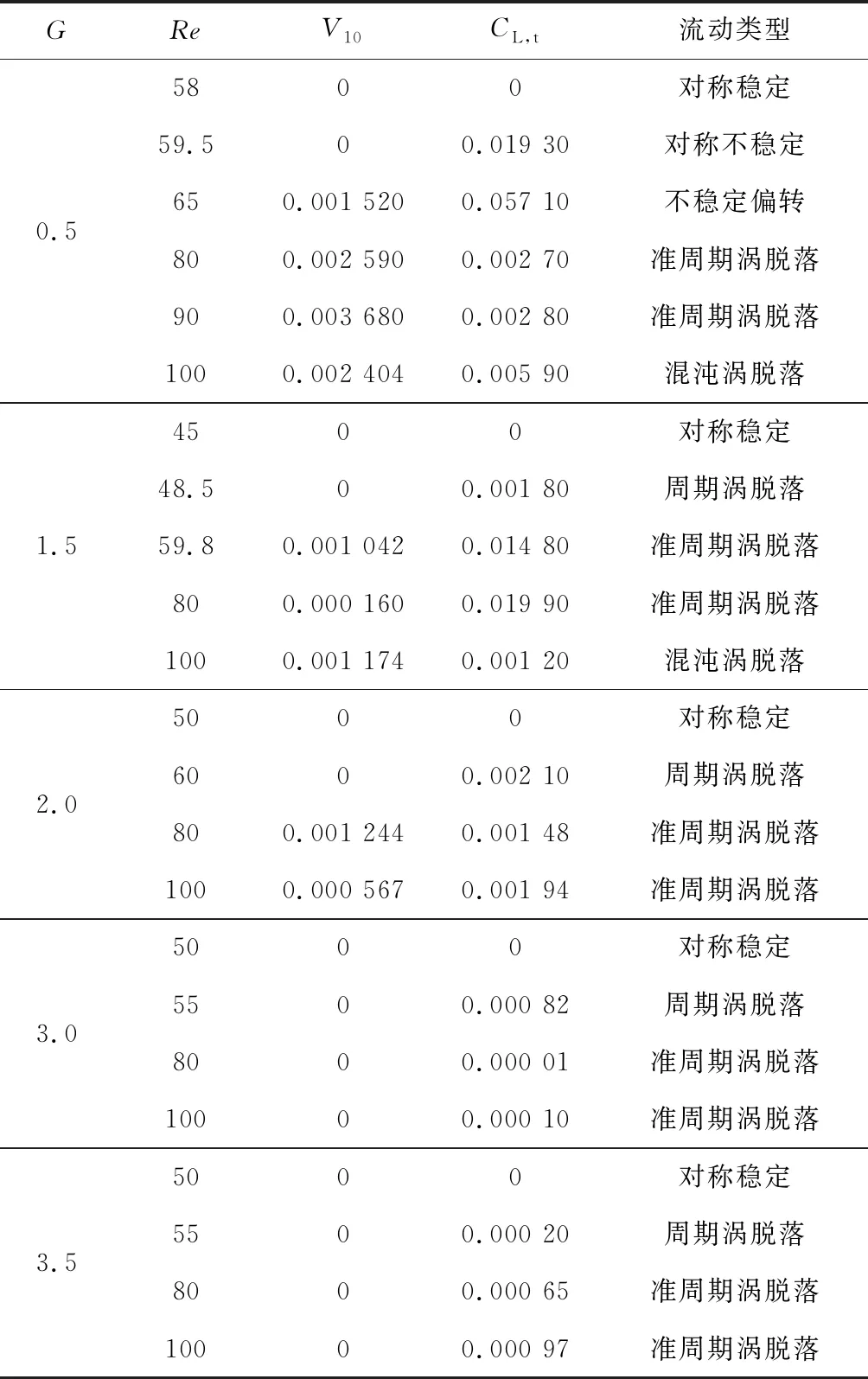
表3 空气横掠椭圆管束的数值模拟结果
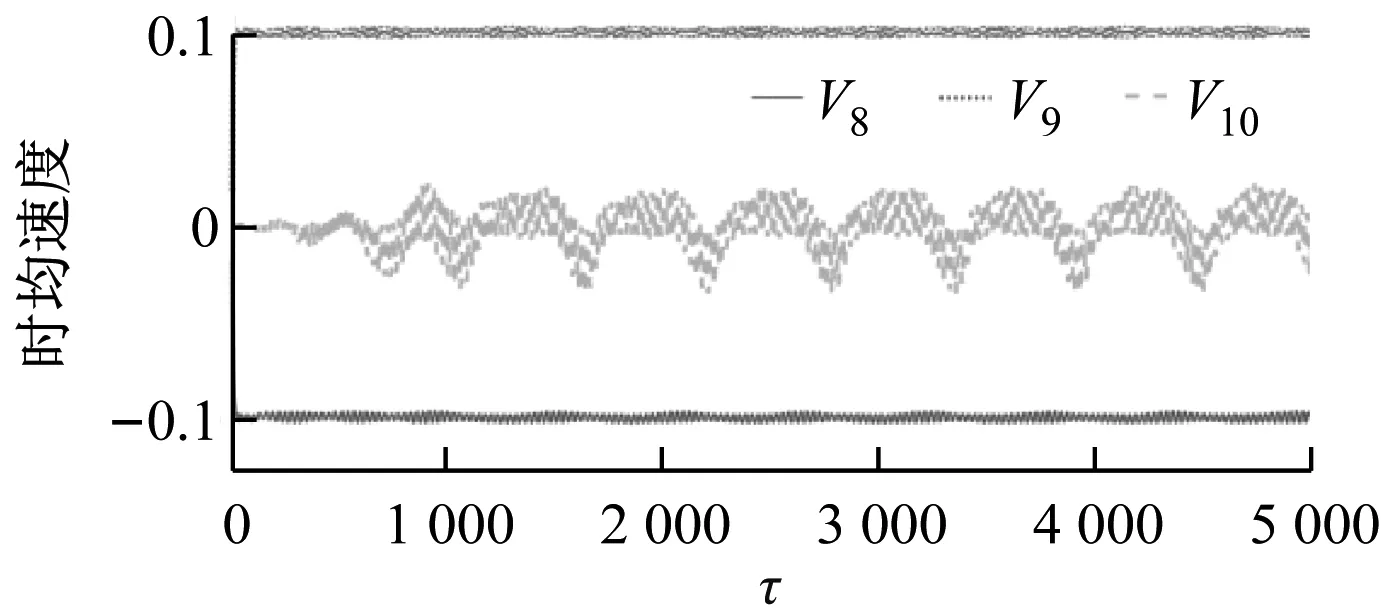
根据CL,t的大小对涡脱落的情况进行分析,通过二分法不断逼近,计算得到相应的Hopf分岔临界雷诺数Re。当CL,t大于0时,尾迹中开始发生涡脱落,稳定流动转变为振荡流动。随着Re的增大,当V10大于0时,说明在Y方向间隙流动开始发生偏转,尾迹流动类型从周期振荡变为准周期振荡。当Re增大到100、G不大于1.5时,系统最终进入混沌状态;G大于1.5时系统最终进入准周期状态。
图3为V10随雷诺数的变化情况,不同的无量纲管间距会引起同一系统中分岔的雷诺数临界值发生变化。在无量纲管间距G=0.5下,Re=59.5时系统发生Hopf分岔,Re=65时发生音叉分岔;在无量纲管间距G=1.5下,Re=48.5时系统已经发生了Hopf分岔,Re=59.8时发生音叉分岔。
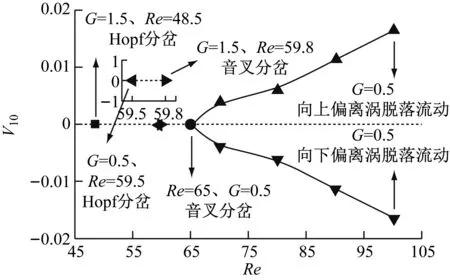
图3 监测点10在Y方向的时均速度分岔图
4 不同无量纲管间距下流动非线性分析
4.1 G=0.5时的流动非线性
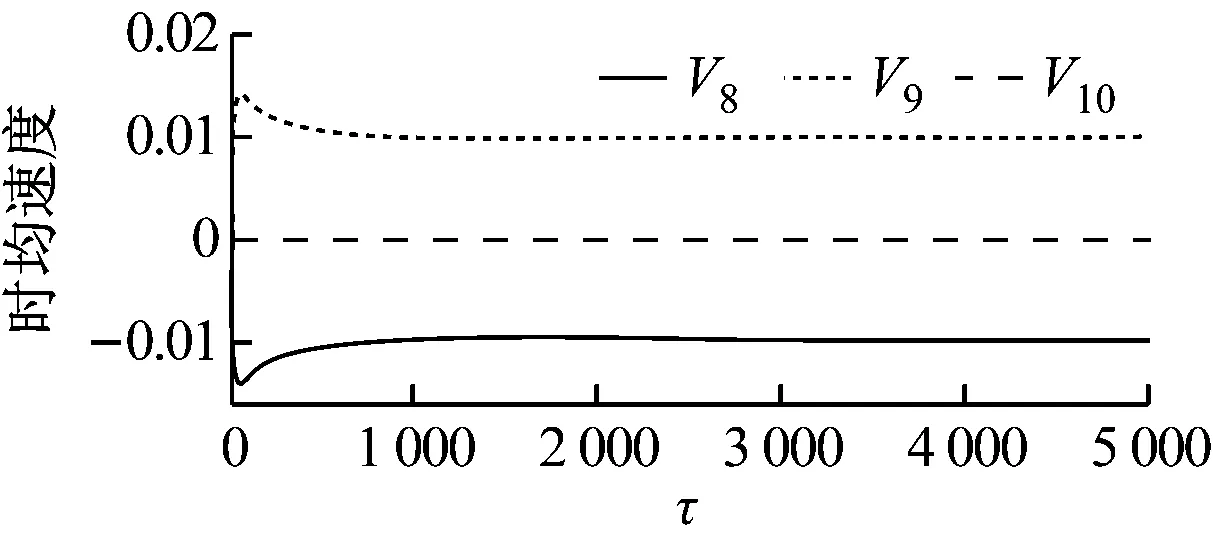
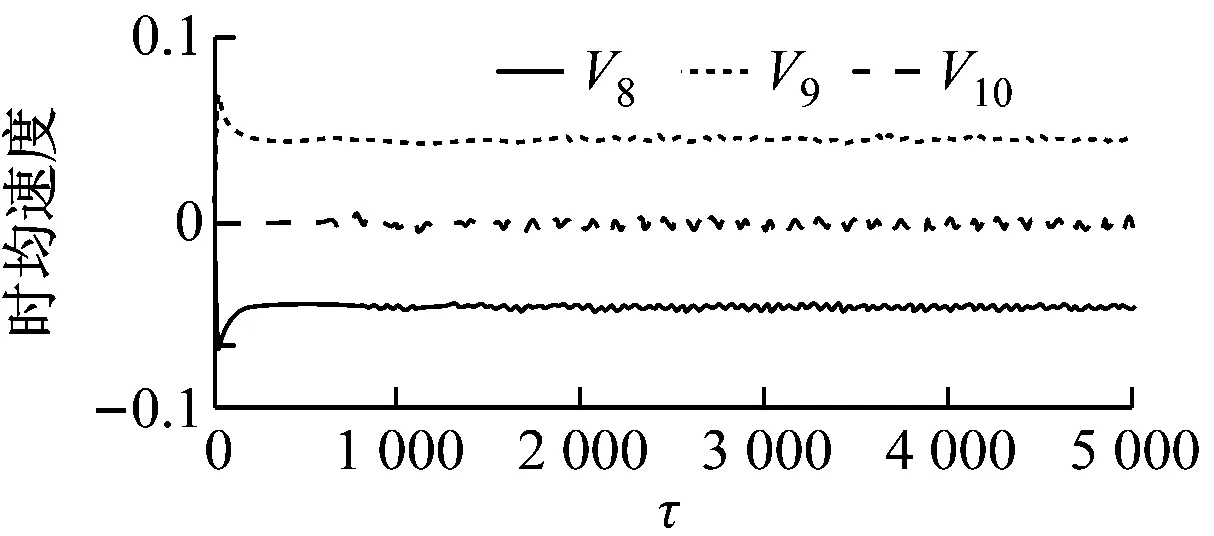
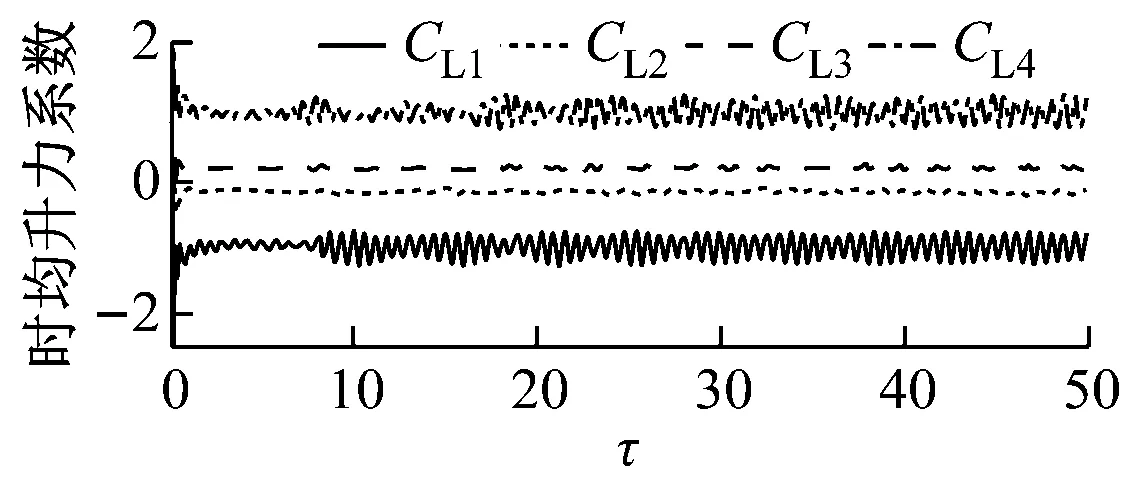
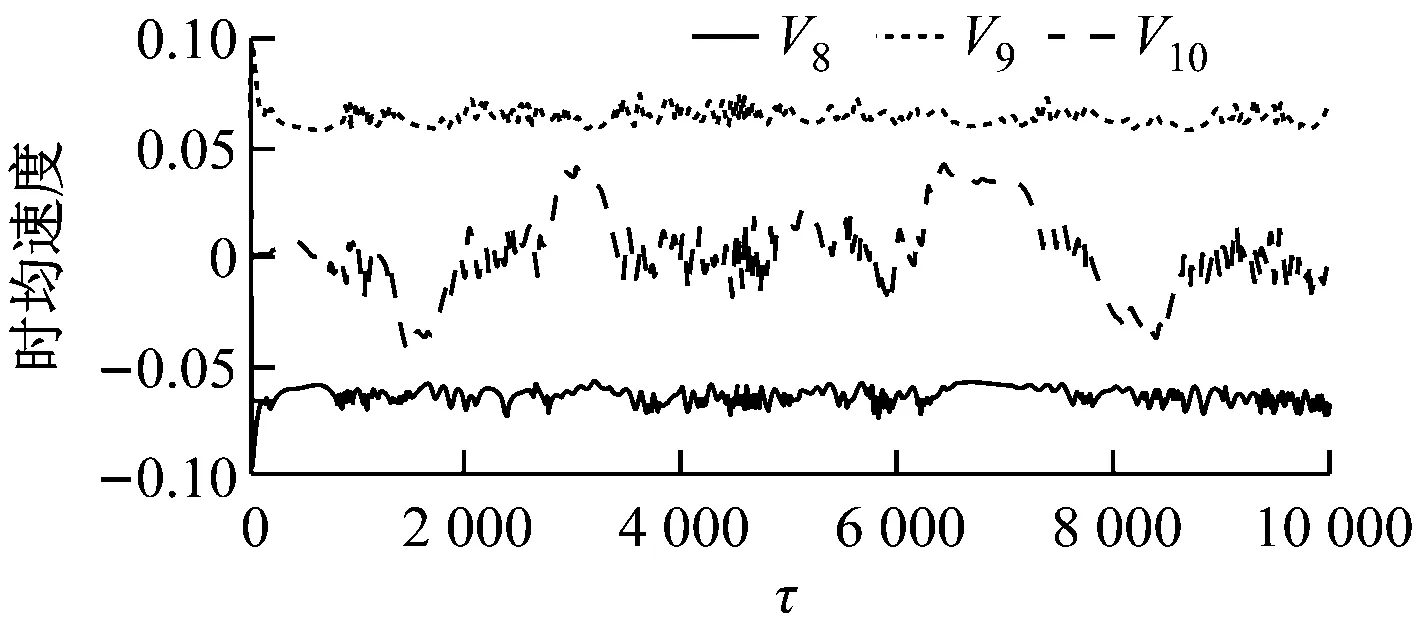
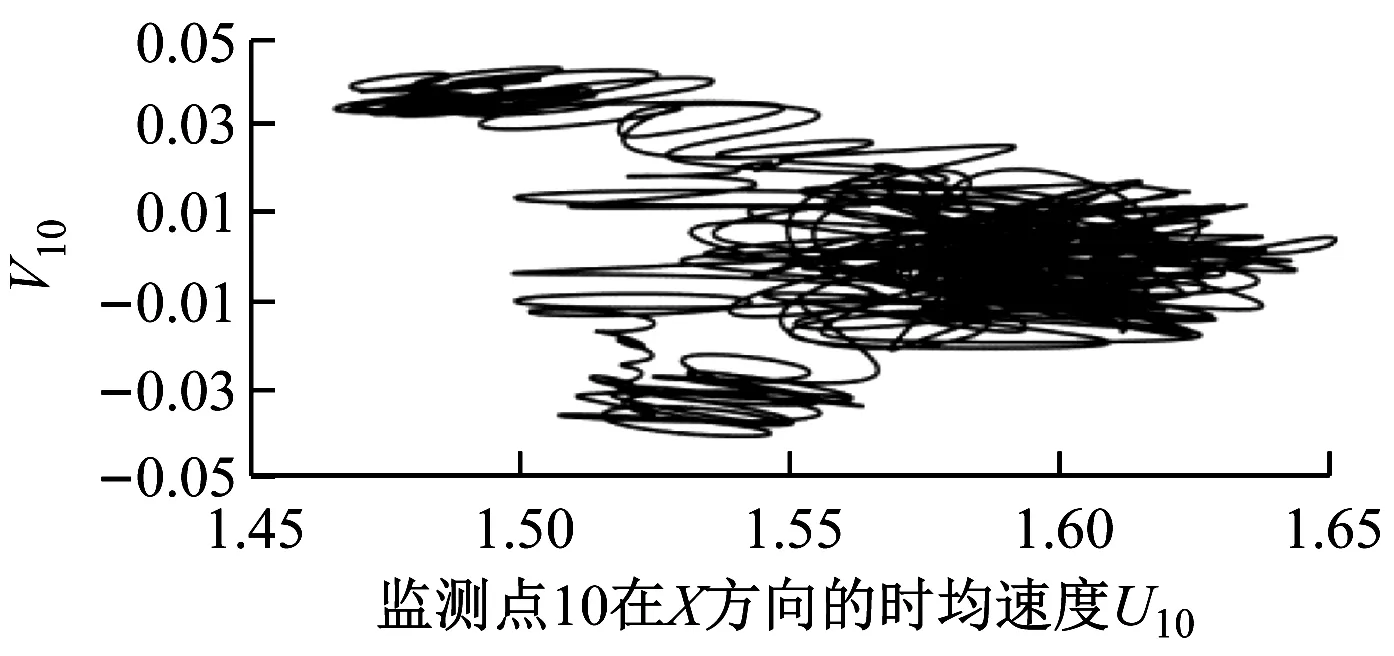
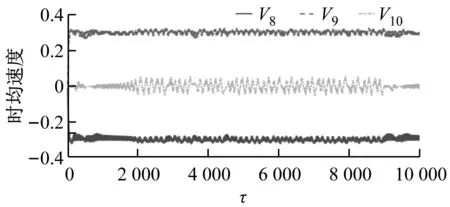
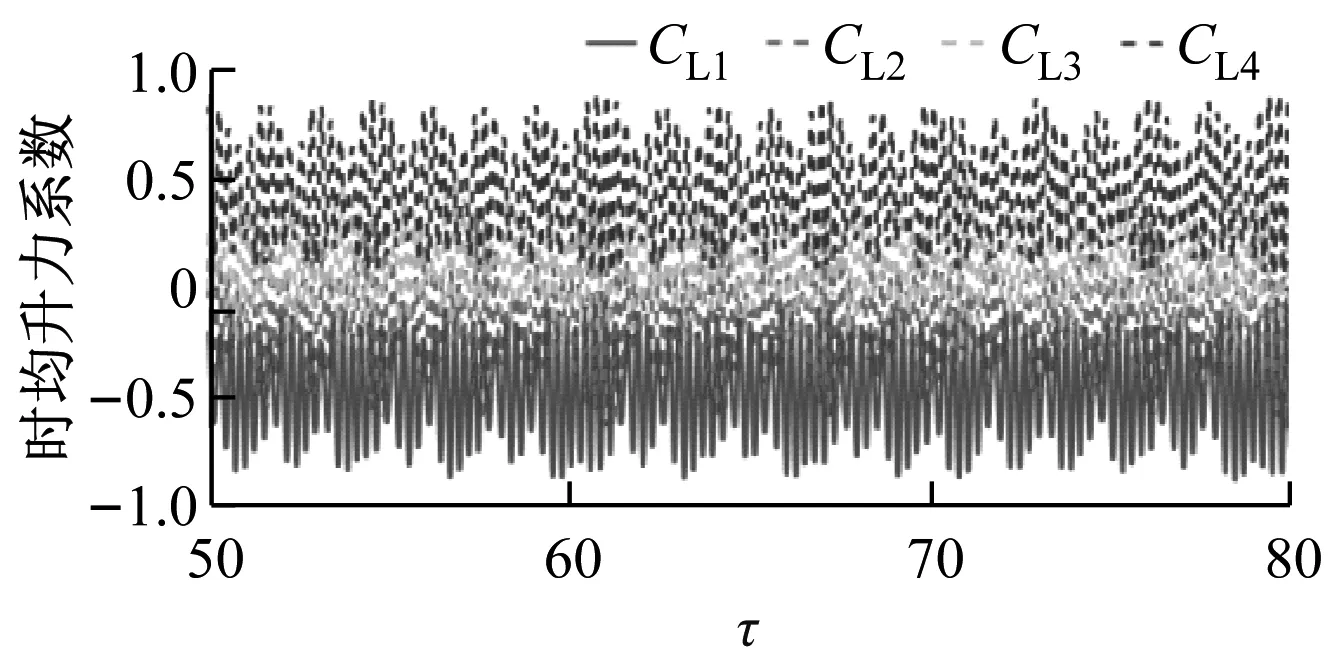
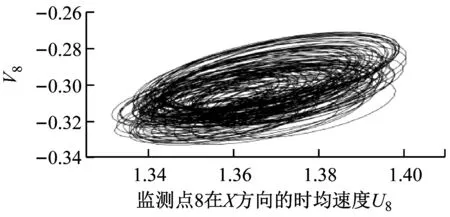
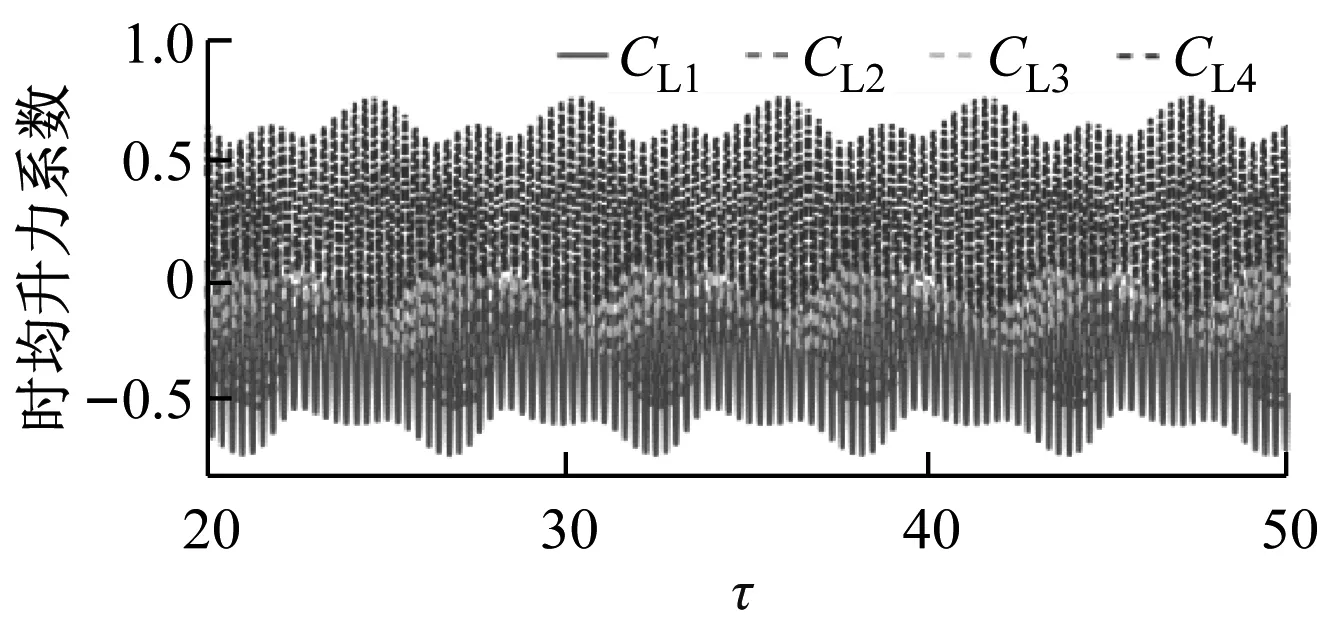
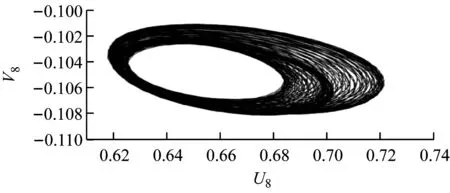
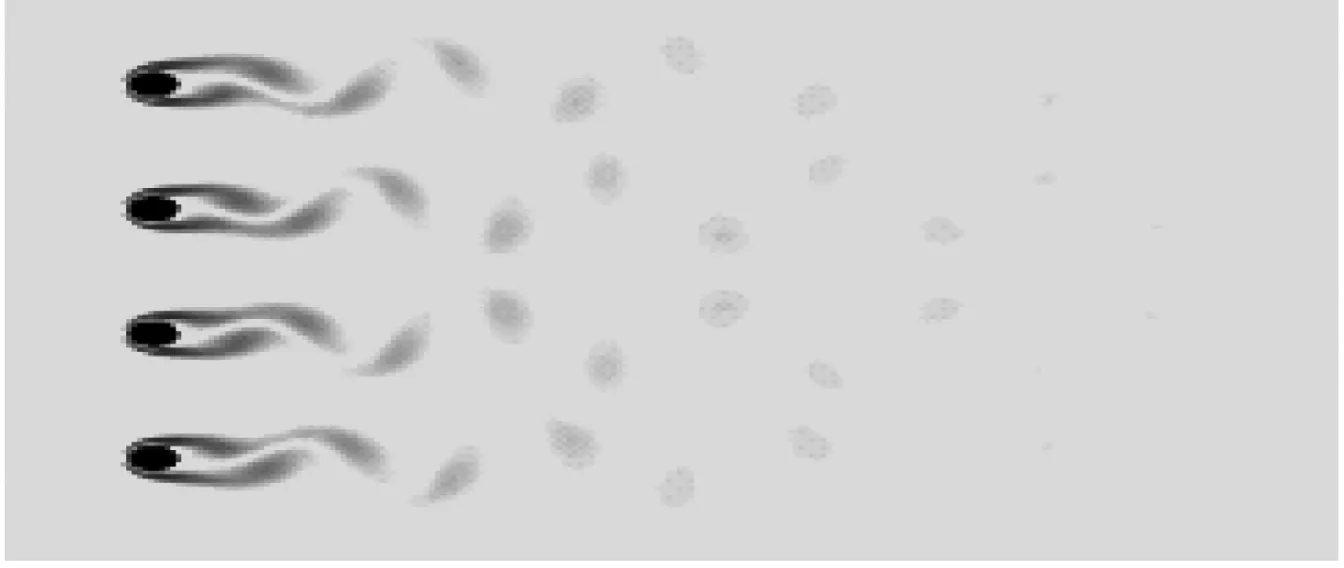
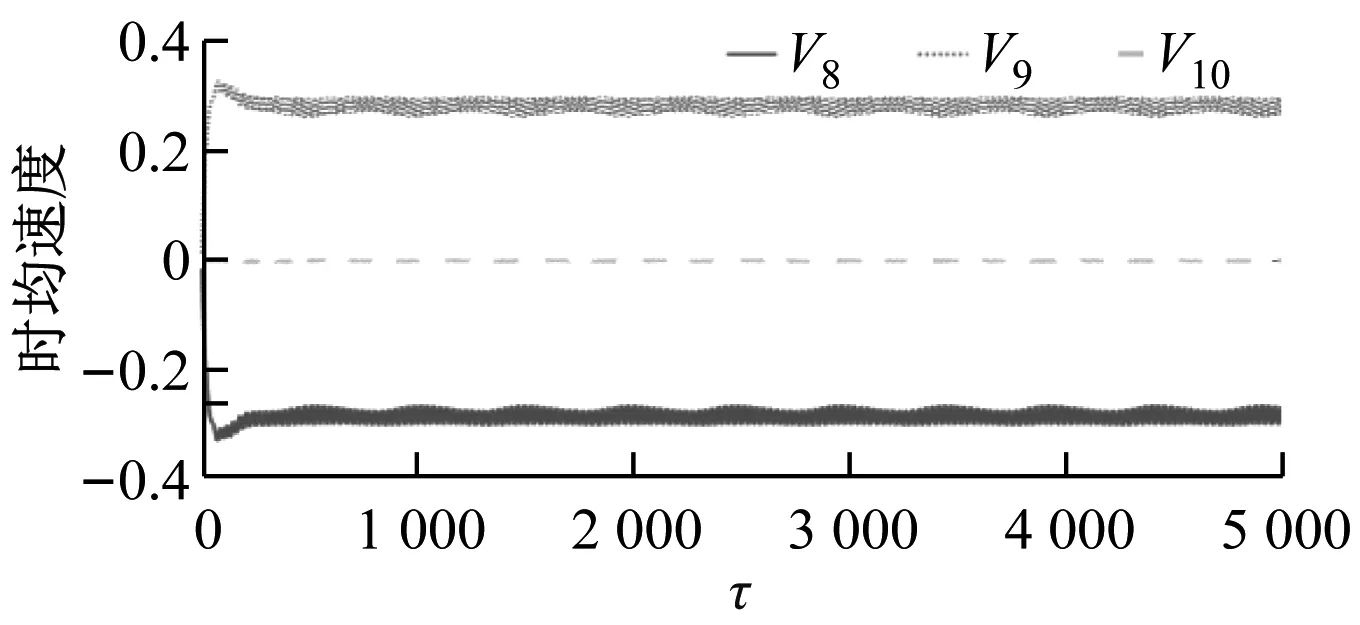
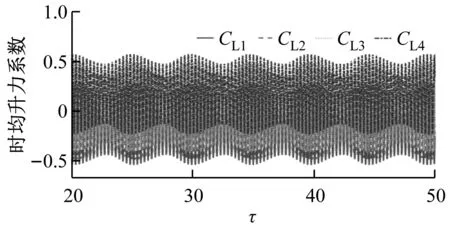
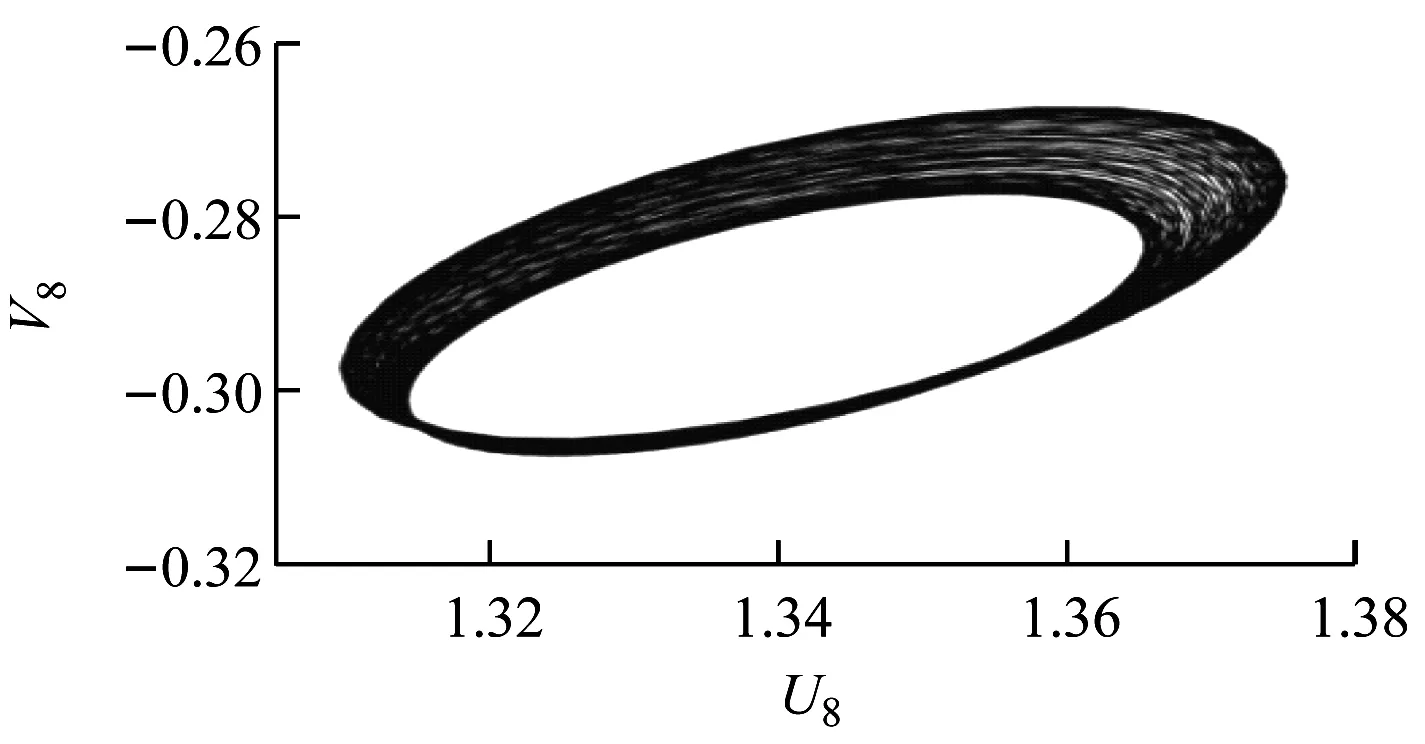
如图4所示,G=0.5、20 如图5所示,当Re增大至59.5时,由于Hopf分岔的发生,2个外部椭圆管的后方开始出现对称涡脱落;3个监测点在Y方向的时均速度不随时间发生变化;椭圆管束的时均升力系数开始出现微弱的规律波动,系统进入准周期状态。 如图6所示,Re=65时管束间隙后方的尾迹流动发生了肉眼可见的偏离;3个监测点在Y方向的时均速度均发生波动;音叉分岔的发生使得内外椭圆管之间的相互作用加剧,椭圆管束的时均升力系数随时间开始出现不等振幅的规律波动,系统进入准周期状态。 (a) 涡量图 (b) 不同监测点在Y方向的时均速度 (c) 椭圆管束的时均升力系数 (a) 涡量图 (b) 不同监测点在Y方向的时均速度 (c) 椭圆管束的时均升力系数 (a) 涡量图 (b) 不同监测点在Y方向的时均速度 (c) 椭圆管束的时均升力系数 如图7所示,Re=100时流体通过椭圆管之间的间隙后发生偏转,形成了不稳定振荡,椭圆管2后方的尾迹向上偏转;3个监测点在Y方向的时均速度和椭圆管束的时均升力系数随时间呈无规律变化,没有固定的振幅和周期,系统进入了混沌状态。 (a) 涡量图 (b) 不同监测点在Y方向的时均速度 (c) 椭圆管束的时均升力系数 (d) 监测点10的速度相图 如图8所示,G=1.5、Re=100时椭圆管束后方的涡脱落是同相同步的。雷诺数较小时,涡脱落之间的相互作用发生在下游尾迹区,随着雷诺数的增大,逐渐朝上游移动;3个监测点在Y方向的时均速度随时间发生相对规律的振荡,这是因为无量纲管间距的增大使间隙流动从随意偏转逐渐过渡到相对规律的上下偏转;椭圆管束的时均升力系数随时间发生相对规律的周期振荡,且外部椭圆管的时均升力系数振幅大于内部椭圆管;系统从混沌状态进入准周期状态。 (a) 涡量图 (b) 不同监测点在Y方向的时均速度 (c) 椭圆管束的时均升力系数 (d) 监测点8的速度相图 如图9所示,G=2.0、Re=100时发生上部2个椭圆管同相、下部2个椭圆管反相的涡脱落情况,这是因为此时内外椭圆管具有不同的涡脱落频率,内外管束后方的涡脱落产生了相位差;3个监测点在Y方向的时均速度随时间不再发生简单的上下振荡,而是产生规律的周期振荡,这是因为间隙流动不再发生偏离,而是随着尾迹涡脱落发生摆动;椭圆管束的时均升力系数发生周期性的双振幅振荡;系统进入了准周期状态。 如图10所示,G=3.0、Re=100时椭圆管后方形成了近似独立的反向卡门涡街脱落;整个过程中,监测点10在Y方向的时均速度未发生波动;椭圆管束的时均升力系数呈规律的周期振荡;系统进入准周期状态。 (a) 涡量图 (b) 不同监测点在Y方向的时均速度 (c) 椭圆管束的时均升力系数 (d) 监测点8的速度相图 (a) 涡量图 (b) 不同监测点在Y方向的时均速度 (c) 椭圆管束的时均升力系数 (d) 监测点8的速度相图 无量纲管间距G=3.5时,椭圆管后方尾迹流动状态与G=3.0时类似,在Re=100下椭圆管束后方形成了4个独立的涡街,G不再对流动状态产生影响,系统进入准周期状态。 (1) 较小的无量纲管间距(G<1.5)会使间隙流动发生偏转入射,音叉分岔的发生加剧了尾迹的相互干扰,随着Re增大至100,系统进入混沌状态。 (2) 无量纲管间距G为1.5~3.5时,尾迹结构从同相流动过渡到反相流动,系统不再发生音叉分岔;随着G的增大,椭圆管束后方的尾迹作用不断减弱,当Re增加到100时,系统进入准周期状态。 (3) 系统可能会出现一系列的分岔点,Re和G的改变均会使流动过程中分岔点发生改变。
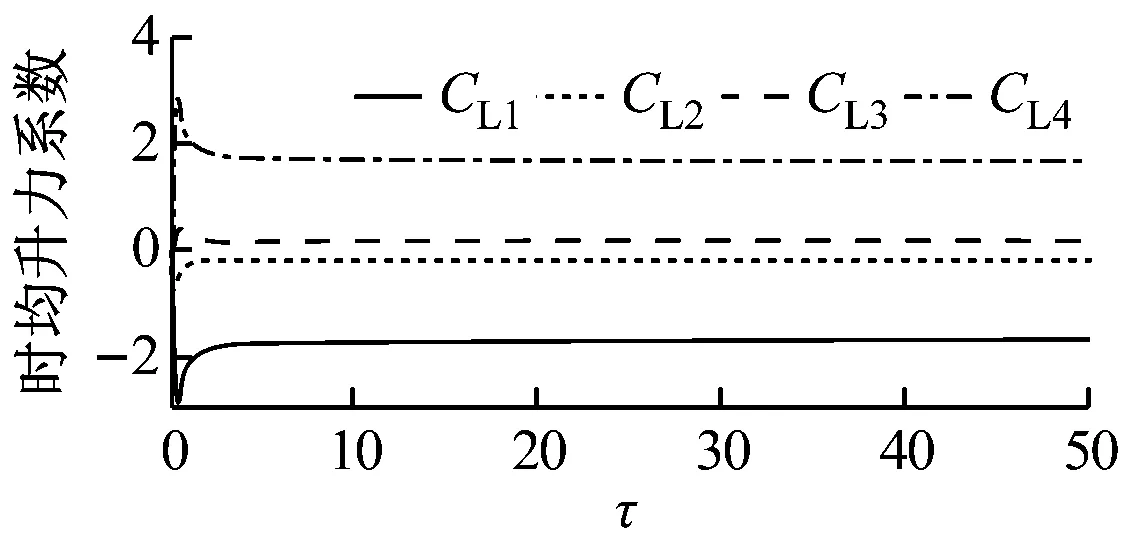


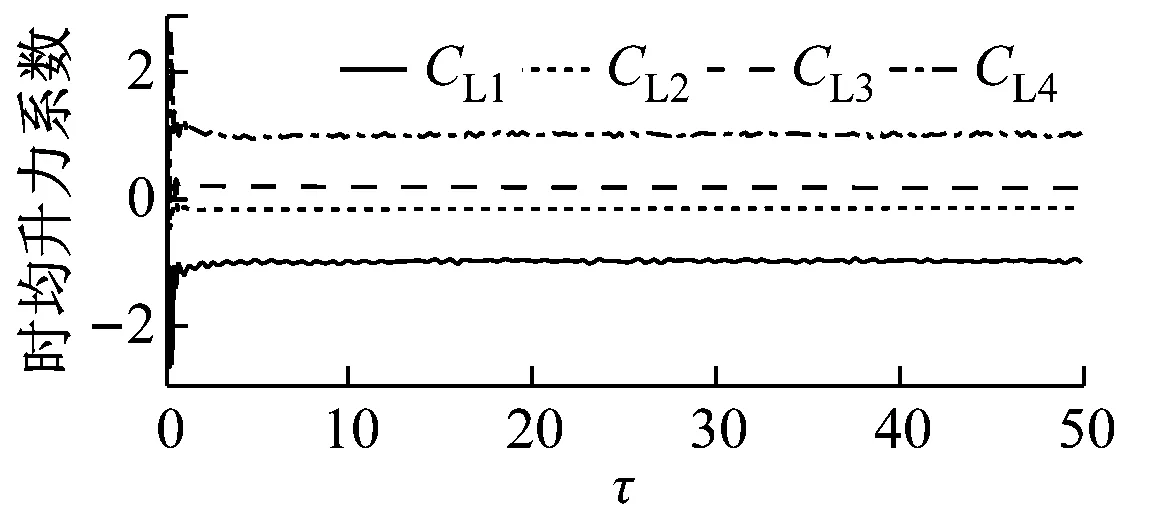



4.2 G=1.5时的流动非线性

4.3 G=2.0时的流动非线性
4.4 G=3.0时的流动非线性

5 结 论
