燃烧器对冲布置锅炉的非对称流动及非线性分析

陈 凯， 杨 茉

(上海理工大学 能源与动力工程学院，上海 200093)

炉膛出口烟气侧热偏差是造成锅炉蒸汽侧热偏差的原因之一，会影响锅炉的安全经济运行。烟气侧温度场与速度场分布不均，使得炉膛出口不同位置的热负荷不同，各受热面吸热不均，从而形成锅炉蒸汽侧热偏差。

针对引起烟气侧热偏差的原因，目前已有学者从锅炉炉内的非对称流动角度进行了分析。王慧等[1]从塔式锅炉炉膛中抽象出二维模型并进行流动的数值模拟，结果表明层流模型和湍流模型下的流场均出现了不对称现象。赵明等[2]对几何结构和物理边界条件完全对称的四角切圆锅炉进行了冷态数值模拟，结果表明随着燃烧器出口速度的增大，切圆中心逐渐偏斜。Yang等[3]对四角切圆布置的塔式锅炉的热态最大连续蒸发量工况进行了数值模拟，发现流场及温度场分布不对称，不同高度切圆均有不同程度的偏斜。沈云羿等[4]计算了不同燃烧器入射角度下炉内温度场的分布，发现当燃烧器入射角度为6°时，炉内流场对称性较好，炉膛出口烟气侧热偏差较小。赵明等[5]通过微调配风使得燃烧器出口速度不对称，从而得到对称的流场及温度场分布，减小了炉膛出口烟气侧热偏差。因此，深入研究锅炉炉内的非对称流动现象对研究热偏差机理具有积极意义。

非对称流动及其非线性特性的研究在不同工程背景下已有许多报道。Fearn等[6]通过实验发现了突扩通道内的非对称流动现象。Hawa等[7]则从方程的角度更加详细地研究了突扩通道内解的分岔现象并求解出分岔点。Shen等[8]通过数值模拟发现了封闭圆内开缝圆在不同开缝方向、不同开缝角度下均存在非对称流动现象。申春赟等[9]指出随着瑞利数(Ra)变化，圆环内流动会从稳态发展为混沌。郑建城等[10]则给出了封闭圆内开缝圆的4种特征解，并通过相图和功率谱图等研究方法进行了非线性特性分析。Wang等[11]和Zhao等[12]发现方腔内流场也存在非对称流动现象及其解的分岔。Zhou等[13]通过直接模拟(DNS)、大涡模拟(LES)和雷诺应力模拟(RSM)3种方式模拟了从低雷诺数(Re)到高雷诺数范围内圆柱绕流通道的流场并进行了时间序列与相图分析，发现流场由对称发展为不对称，并给出了3种特征解。综上所述，非对称流动现象存在于各种实际过程中，而通过非线性特性分析可以更好地认识物理问题及其特征解。

然而，目前关于炉内非对称流动现象的理论研究较少，且尚未有研究者通过相图与频谱分析等非线性特性研究方法对其特征解及解的分岔进行深入分析。因此，笔者基于文献[1]～文献[3]的基本观点，以燃烧器对冲布置的锅炉为研究对象，根据炉膛几何结构建立物理边界条件完全对称的二维模型，采用Reynolds时均方程法对冷态流场进行数值模拟，比较不同燃烧器出口Re下流场对称性的变化情况，并利用相图和频谱分析等研究方法对其中的特征解进行非线性特性分析，为进一步认识锅炉炉内的非对称流动现象奠定基础。

1 物理模型及数学模型

1.1 物理模型

根据燃烧器对冲布置锅炉炉膛的结构，建立关于中心线对称的二维几何模型(如图1所示)，计算域包括冷灰斗区和主燃烧区。为了使本研究具有普遍性，笔者忽略上层燃烧器，仅考虑底部一层燃烧器对冲布置的情况。假设燃烧器喷口均匀进风，喷口速度大小通过燃烧器出口Re表征，设置速度边界条件为对称，并在炉膛中部设有速度监测点。假设冷灰斗底部封闭为固体壁面，所有固体壁面均采用无滑移假设，出口采用局部单向化假设。通过ICEM软件对计算域各分区进行网格划分，冷灰斗区采用非结构化三角形网格，主燃烧区采用结构化四边形网格，对燃烧器喷口对冲区域及近壁面的网格进行局部加密，计算域网格如图2所示。经过网格无关性验证，最终确定网格数为5.6万。

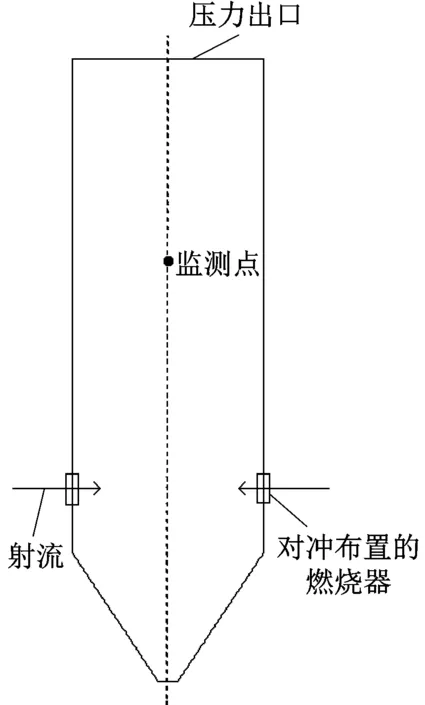
图1 锅炉模型示意图

1.2 数学模型

采用Reynolds时均方程法对炉内冷态流场进行数值模拟，近似模型采用Reynolds应力模型，求解采用具有QICK差分格式的Simple算法，整个求解过程在Fluent软件中进行。Reynolds时均方程为：

图2 计算域网格

(1)

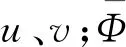
求解Reynolds时均方程得到的时均值与实际流场的瞬时值存在一定差异。但目前已有大量实验证明时均值与实际流场中的平均值基本一致，因此时均值的非线性特性基本可以反映实际流场平均值的非线性特性。

2 计算结果及分析

2.1 燃烧器出口Re对炉内流场的影响

实际锅炉炉内的流动是空气携带煤粉颗粒与其燃烧产物的多组分流动，但考虑产物浓度所引起的速度变化很弱甚至可以忽略，所以通过空气来研究炉内流体的流动规律。

图3给出了不同燃烧器出口Re下炉内稳定阶段的瞬态流场。从图3可以看出，当Re=6 000时，流线完全对称，主流处于中间位置，炉膛左右两侧形成对称的回流区，说明此时炉内不存在非对称流动。当Re=8 000时，流线仍完全对称，但主流左右两侧的回流区长度增加。当Re=10 000时，流线开始转变为非对称分布，主流轻微偏斜，说明炉内存在非对称流动；主流左右两侧分别形成2个涡旋，互相挤压但未移动到另一侧。当Re=14 000时，主流左右两侧仍分别存在2个涡旋，但主流偏斜程度增加。当Re=20 000时，流线完全不对称，由于左右两侧涡旋互相挤压且此时湍流脉动较强，原先位于左侧的涡旋移到右侧。当Re=200 000时，由于速度增大，处于旺盛湍流，湍流脉动剧烈，流场内产生更多的涡旋，流线极其不对称。

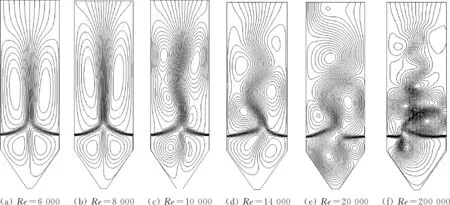
图3 不同Re下稳定阶段的瞬态流场

图4给出了不同高度流体速度随燃烧器出口Re的变化情况，其中横坐标x/L为无量纲宽度，纵坐标u/U0为无量纲速度，y/H为无量纲高度，L为炉膛宽度，U0为各工况下燃烧器喷口的出口速度，H为炉膛高度，y/H=0.286为燃烧器喷口所在高度，y/H=0.5、0.625和0.75为下游区域。以下选取图3中6个工况中典型的3个工况(Re=6 000、10 000和20 000)进行分析。从图4可以看出，当Re=6 000时，不同高度流体的速度轮廓均关于轴线对称。燃烧器喷口高度处的速度普遍较高，但由于冷灰斗区存在2个涡旋，速度轮廓的中心峰值较低且左右两侧存在波谷。在下游区域，速度轮廓左右两侧存在波谷是由于主流左右两侧存在涡旋。当Re=8 000时，速度轮廓开始偏离轴线，不同高度流体均有轻微的非对称流动。当Re=20 000时，速度轮廓关于轴线完全不对称，燃烧器喷口高度及下游区域的不对称性均较明显，y/H=0.5、0.75时炉膛左右两侧速度差别较大。

因此，即使几何结构及物理边界条件均对称，炉内仍会出现非对称流动，且随着燃烧器出口Re的进一步增大，涡旋的运动形态各不相同，流场不对称性逐渐增大。

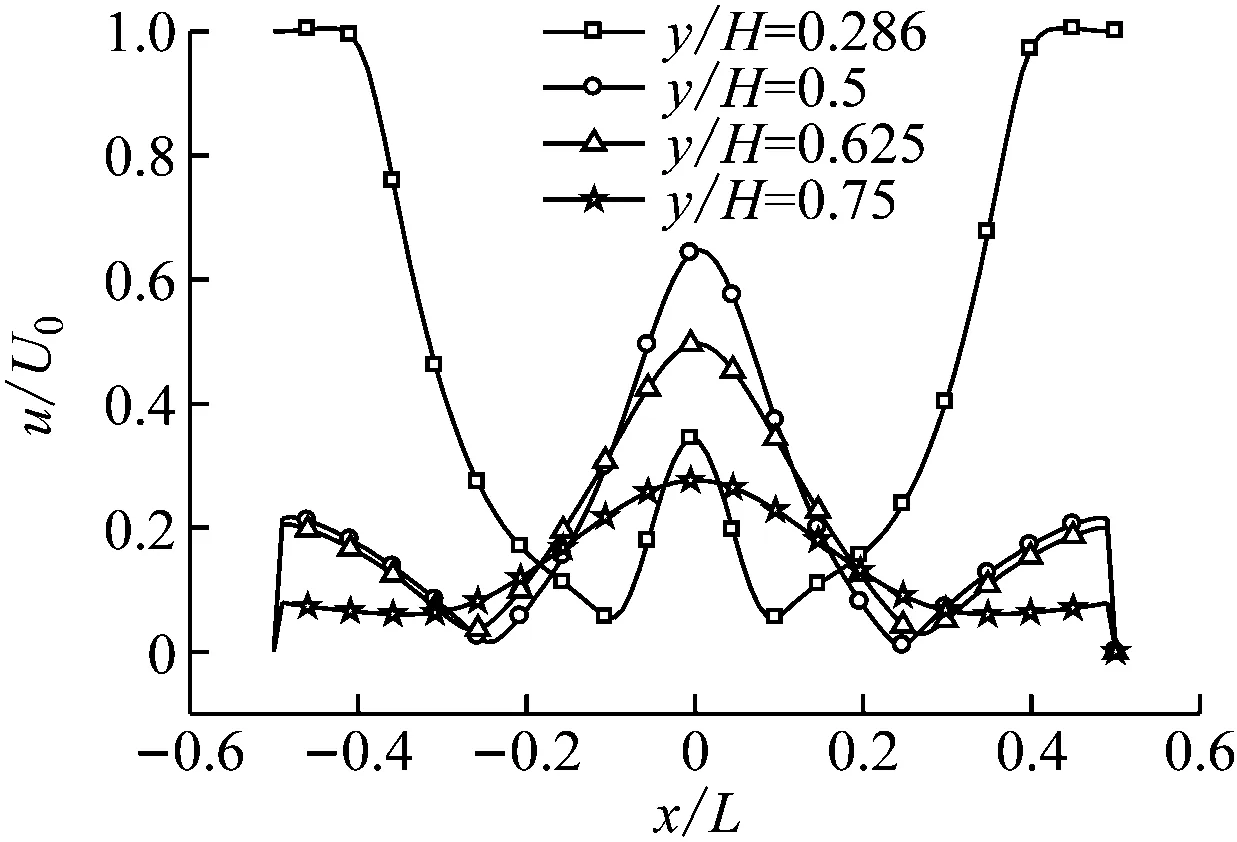
(a) Re=6 000

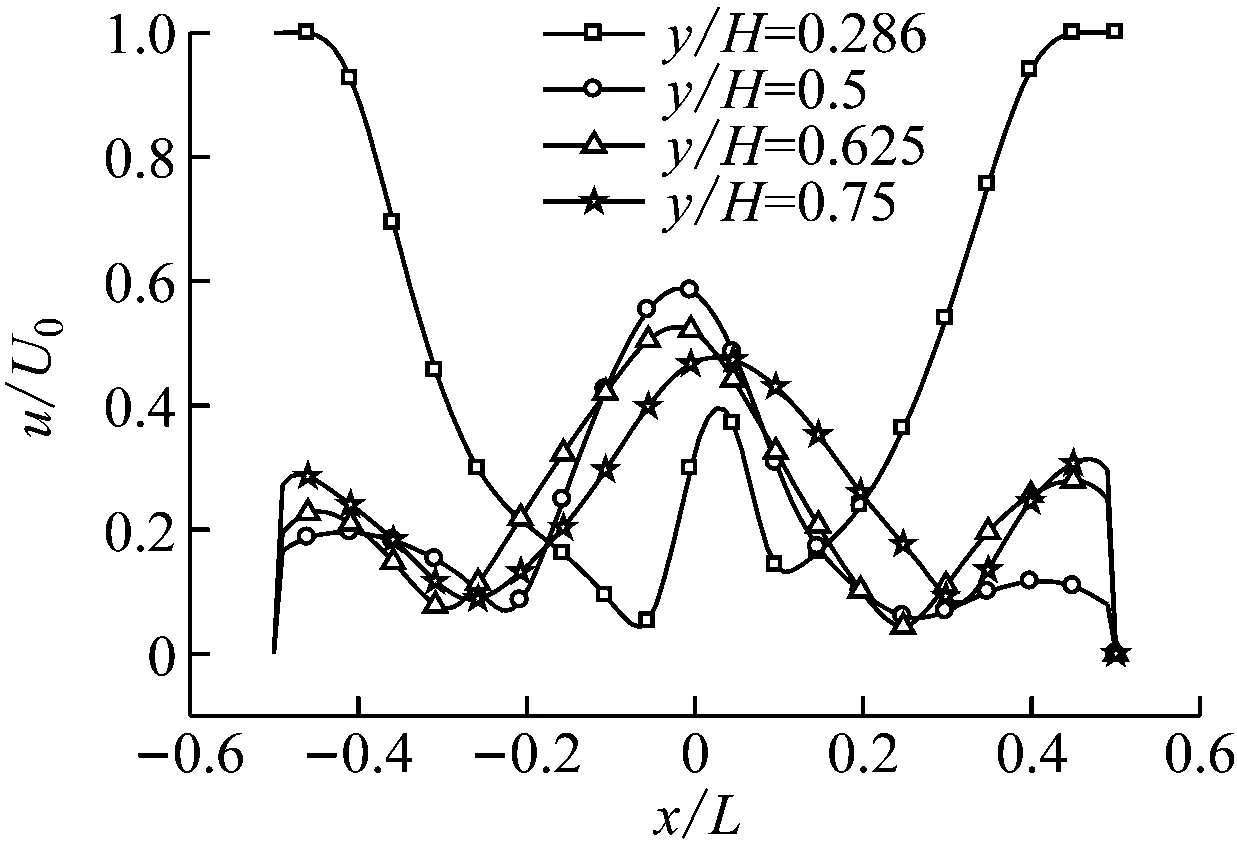
(b) Re=10 000

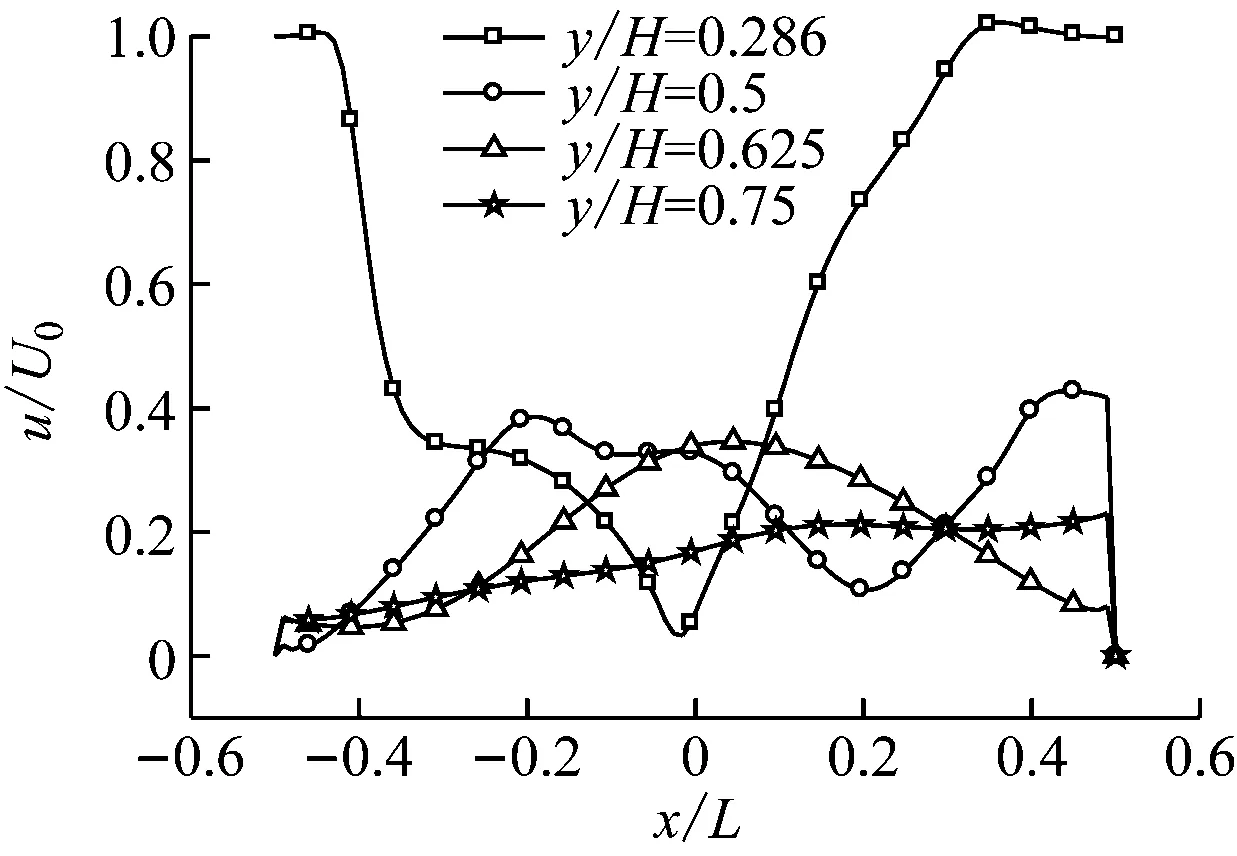
(c) Re=20 000

2.2 流场的非线性特性分析

特征数Re的取值会影响解的非线性特性，一旦Re在临界值附近发生变化，数值解的性质也会随之改变并反映到实际现象中。

2.2.1 速度的时间序列

图5给出了不同燃烧器出口Re下监测点的速度时间序列，其中U为监测点的瞬时速度。由图5(a)可知，当Re=6 000时，速度经过初始阶段的变化后，在稳定阶段不再发生变化，表明计算域内为稳定的定常流动，此时的解为稳定定常解。由图5(b)可知，当Re=10 000时，在稳定阶段速度随时间周期振荡，表明计算域内为稳定的周期性流动，此时的解为周期性振荡解。由图5(c)可知，当Re=20 000时，在稳定阶段速度随时间非周期振荡，表明计算域内出现了混沌流，此时的解为混沌解。这表明随着Re的增大，数值解的性质发生了变化，出现动态分岔现象，反映到流场中即为上述流场对称性的变化。

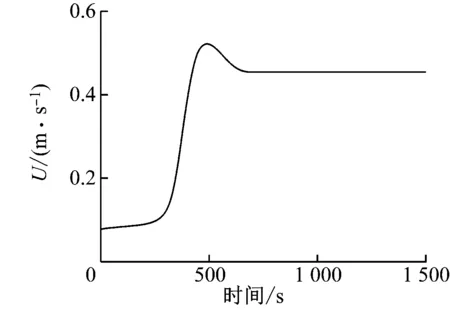
(a) Re=6 000

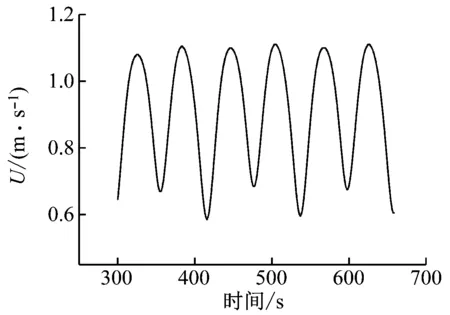
(b) Re=10 000

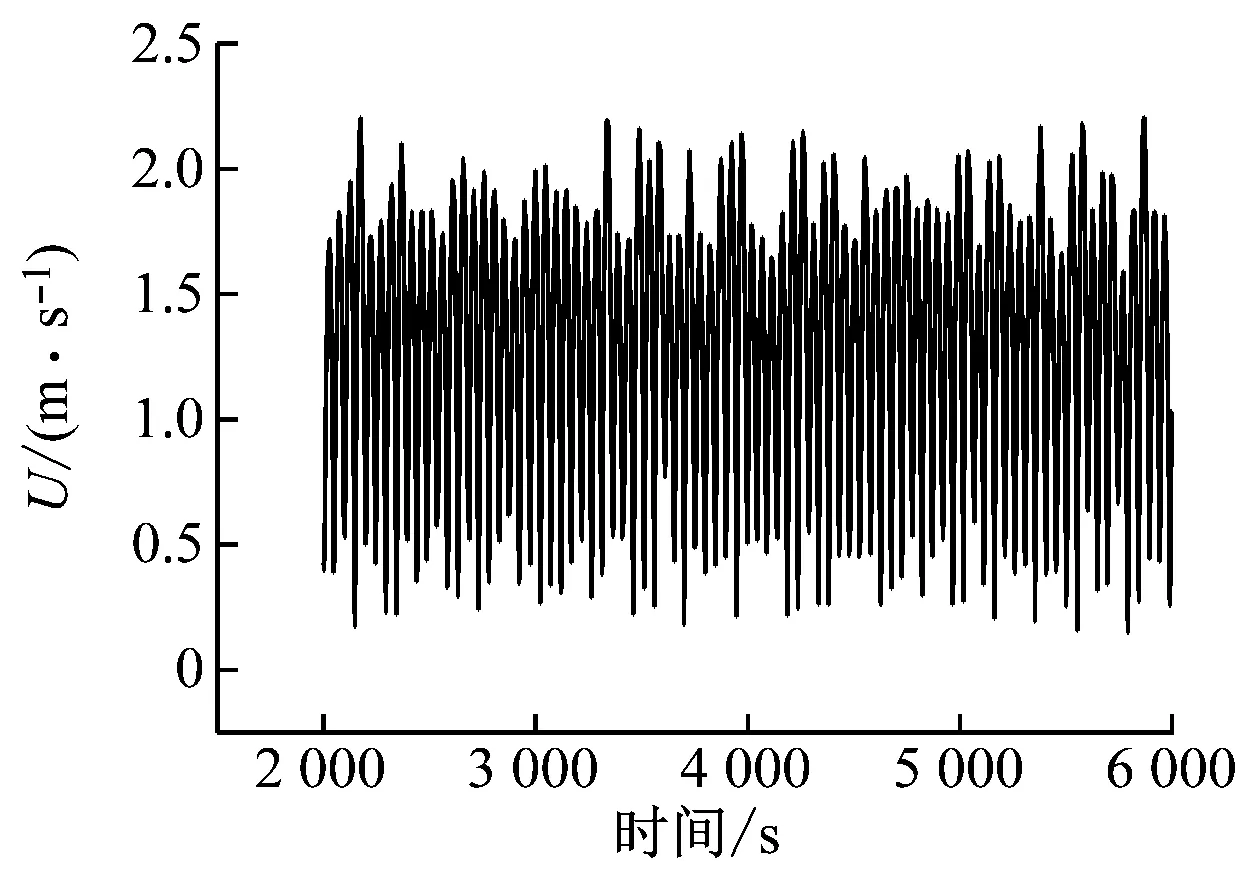
(c) Re=20 000

2.2.2 速度相图分析

图6给出了不同燃烧器出口Re下监测点在稳定阶段的速度相图。由图6(a)可知，当Re=6 000时，速度在相空间中的轨迹随时间发展为相空间中的1个点，将周围的轨道都吸引过来，其吸引子为不动点，也称定常吸引子。由图6(b)可知，当Re=10 000时，速度在相空间中的轨迹分岔为1个折叠的封闭圆环，将周围的轨道吸引到这个周期性的循环中，其吸引子为极限环。由图6(c)可知，当Re=20 000时，速度在相空间中的轨迹虽杂乱无章但局限于一定区域中，其吸引子为混沌态的奇怪吸引子。吸引子性质的变化也反映Re增大过程中出现了动态分岔。

2.2.3 速度频谱分析

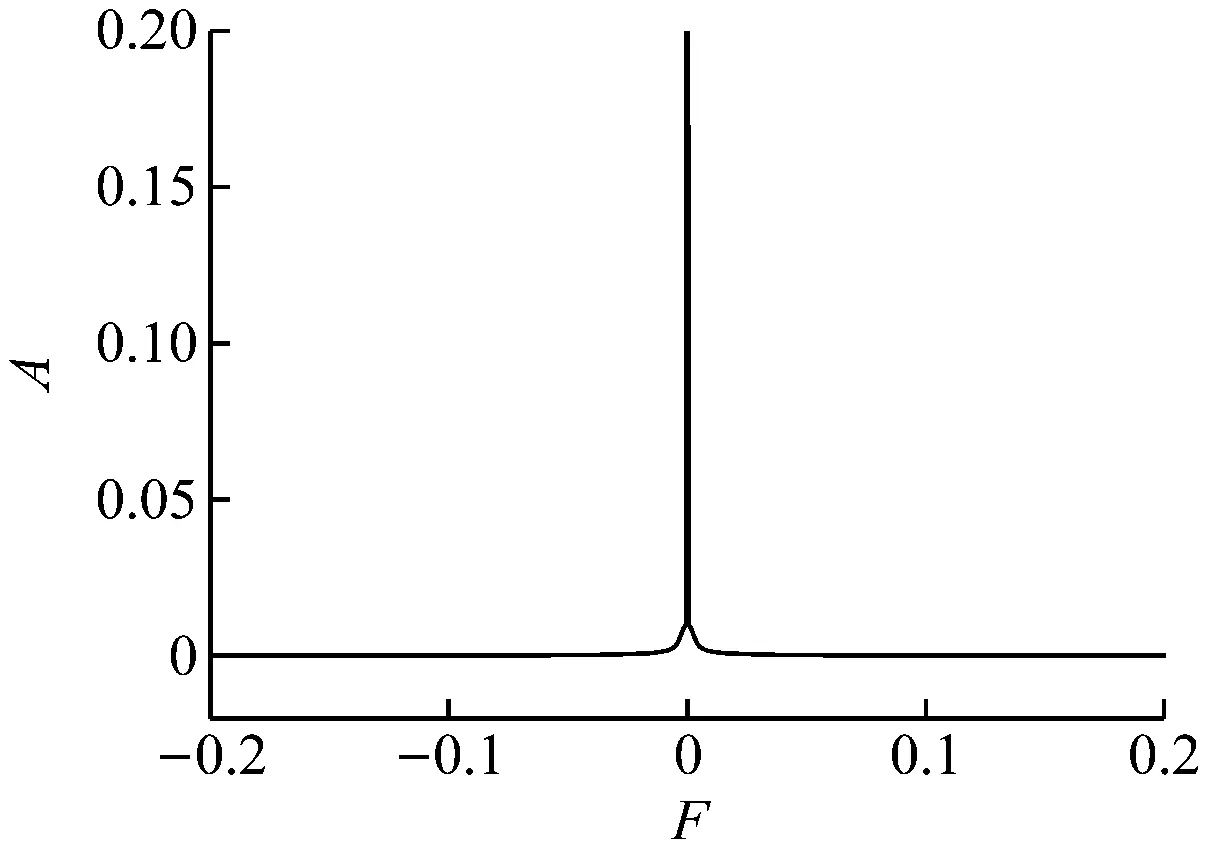
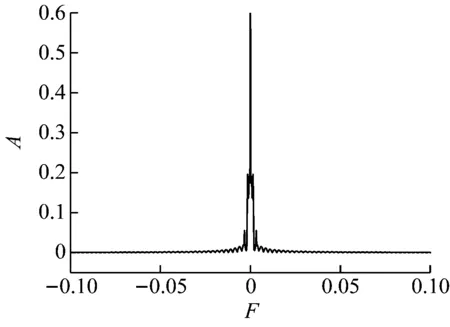
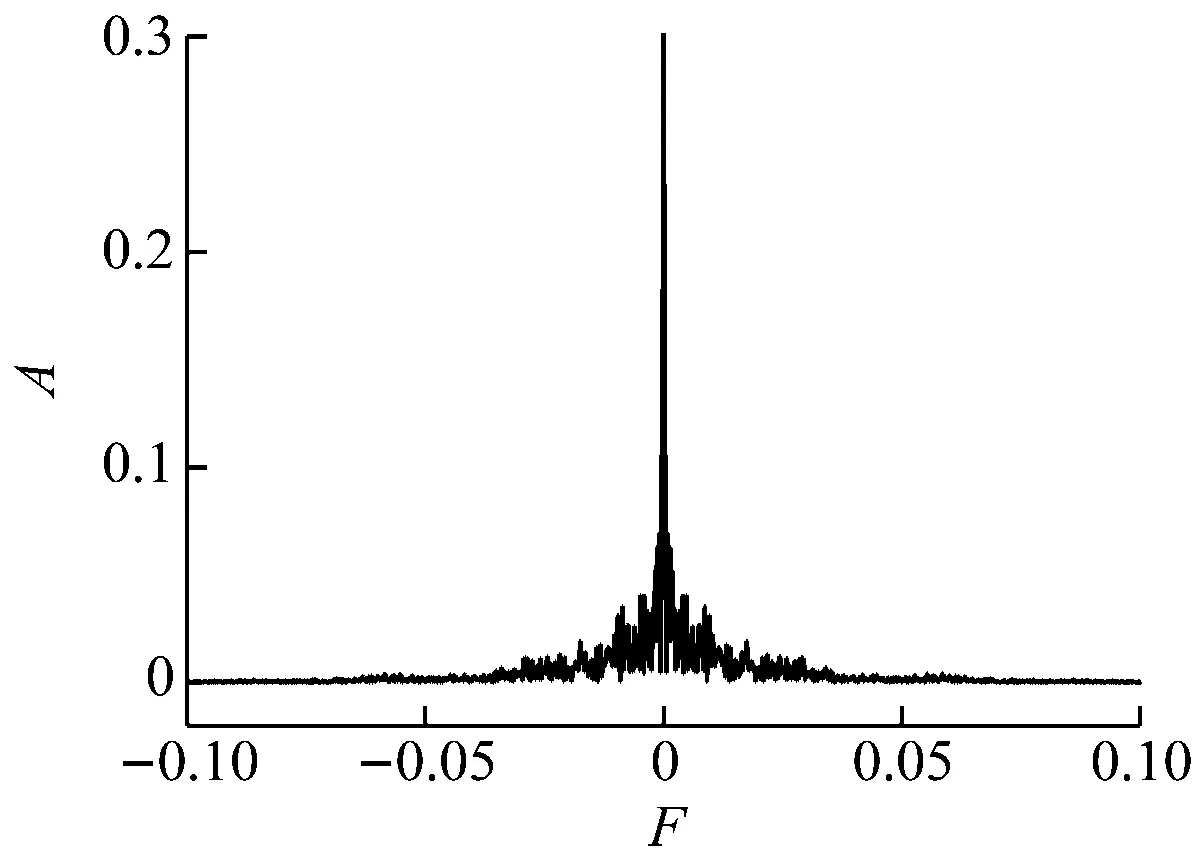
图7给出了不同燃烧器出口Re下监测点速度的频谱图，其中横、纵坐标分别为无量纲化的频率F和振幅A。由图7(a)可知，当Re=6 000时，频谱整齐且未出现其他基频，表明计算采用的数据对整体频率的影响是一致的，未出现分岔。由图7(b)可知，当Re=10 000时，频谱出现1个狭窄的尖峰，即存在1个基频，表明数据对结果的影响并不统一，出现了分岔。由图7(c)可知，当Re=20 000时，频谱除原有的谱峰外，出现了更多的次频，表现为连续频谱。这是由于从稳定定常解发展为非周期振荡解的过程中，每出现1次分岔就会产生新的分频及谱峰。随着分叉的不断进行，频谱会越来越密，频谱图也从离散频谱过渡到连续频谱。

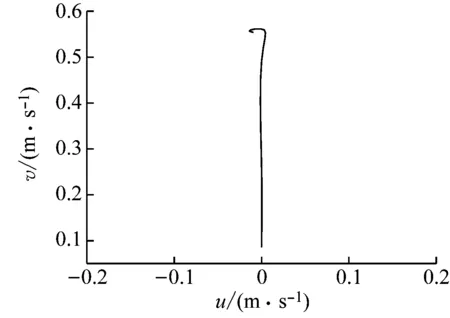
(a) Re=6 000

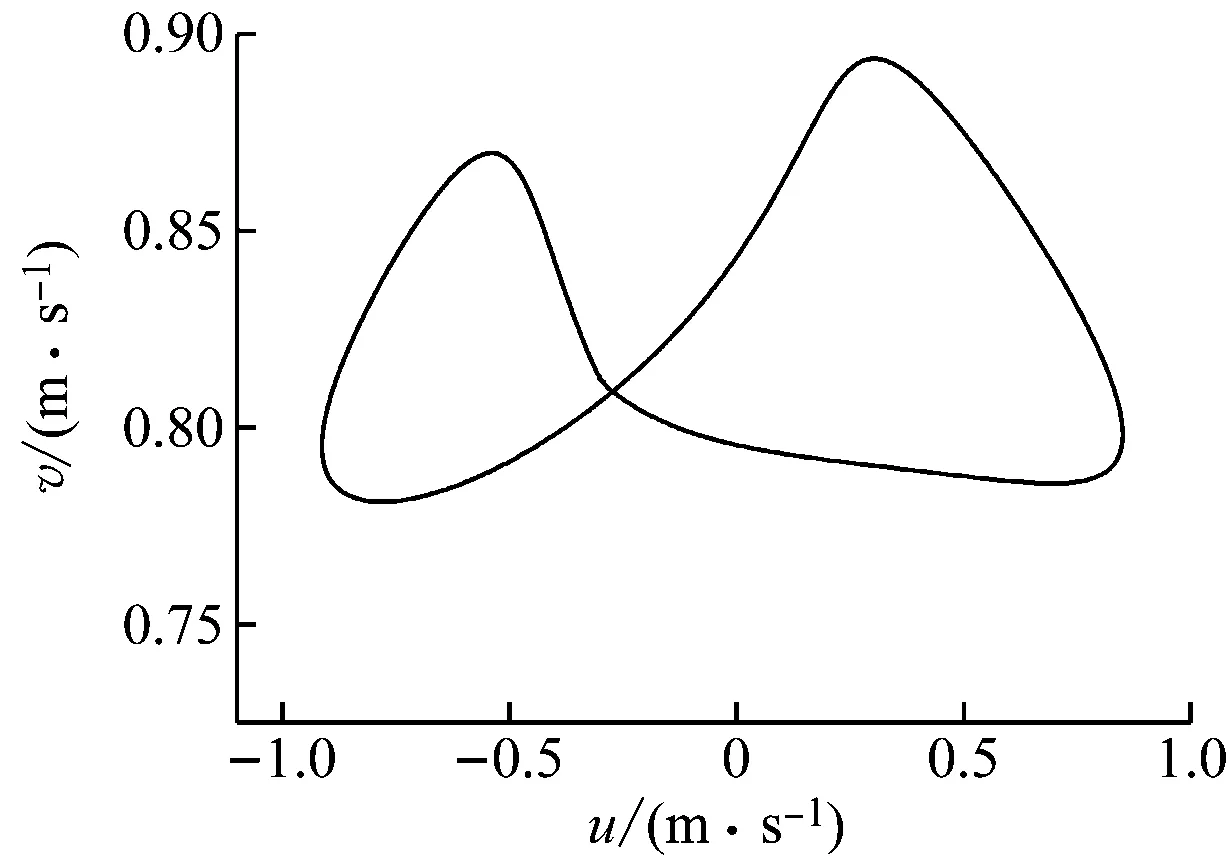
(b) Re=10 000

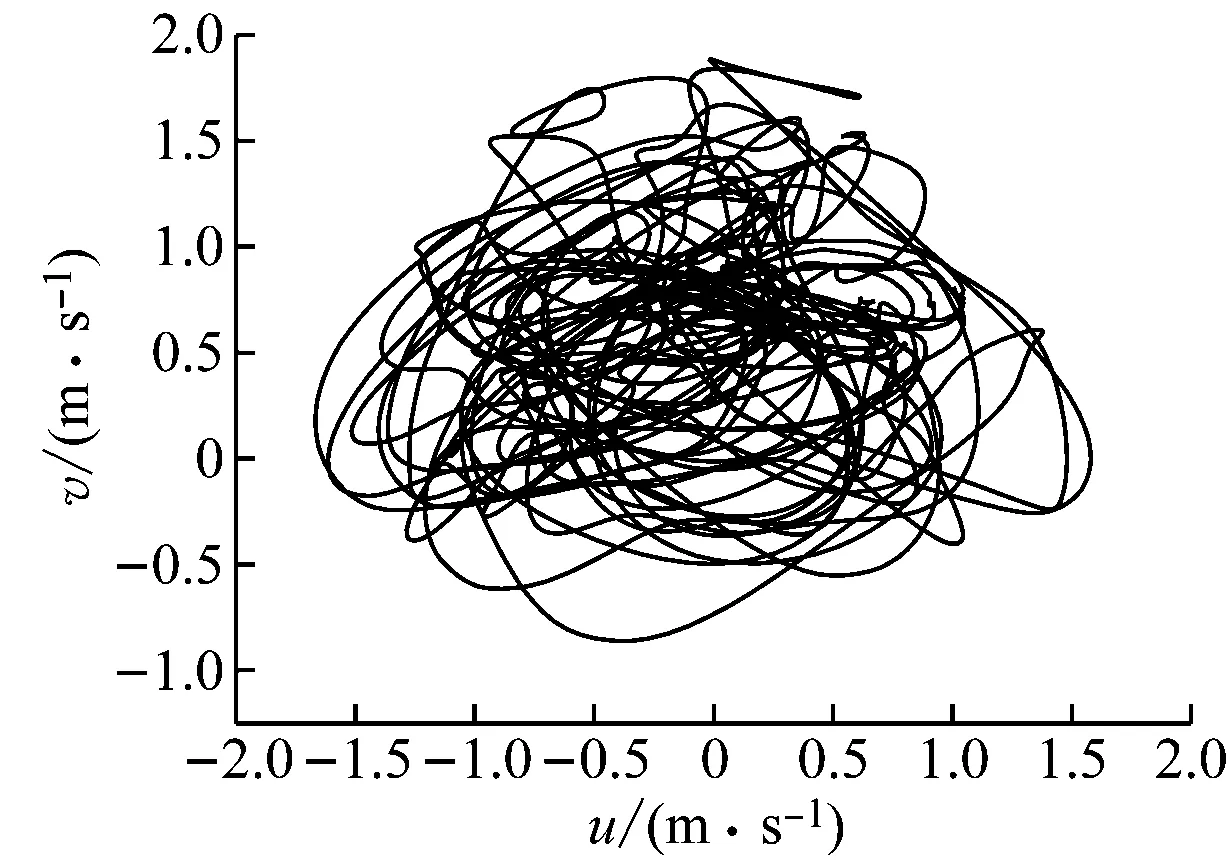
(c) Re=20 000

(a) Re=6 000

(b) Re=10 000

(c) Re=20 000

3 结 论

(1) 即使几何结构及物理边界条件均对称，锅炉炉内仍会出现非对称流动，且随着燃烧器出口Re的进一步增大，流场不对称性逐渐增大。

(2) 炉内出现非对称流动现象的原因在于数值解随燃烧器出口Re的增大出现了动态分岔，存在稳定定常解、周期振荡解和非周期振荡解3种不同性质的解。

(3) 当Re=6 000时，数值解为稳定定常解，流场完全对称，相图最终为不动点，频谱整齐且未出现其他基频；当Re=10 000时，数值解为周期振荡解，开始出现非对称流动，相图为折叠的极限环，频谱出现了1个基频；当Re=20 000时，数值解为非周期振荡解，流场内出现混沌流，相图对应奇怪吸引子，频谱图表现为连续频谱。