基于改进HHT的分钟级超短期风速预测
2021-04-22曾娜梅霍志红邓智文靳志杰
曾娜梅, 霍志红, 许 昌, 邓智文, 靳志杰
(1.河海大学 能源与电气学院,南京 211100;2.河海大学 水利水电学院,南京 210098)
风力发电的大力推广带来很大经济效益的同时,也使风电场面临一些挑战。其中,自然风的随机性与间歇性导致风电机组出力很不稳定[1],严重影响接入电网系统的稳定性,更不利于风电场的调度和控制。精准有效的功率预测是解决上述问题的关键,而准确预测风速是风电场功率预测的基础[2]。通常整个风电场的控制系统从接收指令到响应结束用时在2 min内,因此为了更好地对风电场进行功率控制,亟需建立有效的分钟级超短期预测系统。
超短期功率预测指提前量为0~4 h的滚动预测,被用于机组控制及载荷跟踪[3]。国内外常用的预测方法包括自回归移动平均(ARMA)[4]模型、空间相关性方法[5-6]、支持向量回归(SVR)[7-8]和小波神经网络[9]等。然而上述方法均集中于对预测方法的创新与改进,忽略了待预测物理量自身特性对模型预测效果的影响。由于风速的时间分辨率越小,其紊流特性及非高斯性就越强,对预测模型的要求也就越高,因此,结合数据预处理的组合预测方法成为近期热点研究趋势。李燕青等[10]基于解析模态分解(AMD)对风电功率序列进行分解,但该方法需提前确定信号中的各个频率成分,不具备自适应性。Hong等[3]利用形态学高频滤波器(MHF)将时间序列分解为平均分量和高频分量,但平均分量的划分参数需要大量仿真实验来确定。He等[11]利用小波变换对风速序列进行分解,并采用深度置信网络(DBN)进一步提取分解后子序列的高维特征,但小波基的选取较难。近年来,希尔伯特黄变换(Hilbert-Huang transform,HHT)因具有自适应性、适于非线性和非平稳信号的处理而受到极大关注。赵倩等[8]利用经验模态分解(Empirical Mode Decomposition,EMD)对风电功率序列进行分解,并采用模拟退火(SA)算法对SVR参数进行寻优。考虑到集合经验模态分解得到的高频分量对预测结果的影响,殷豪利用小波包分解对本征模态函数(Intrinsic Mode Function,IMF)分量1进行再分解处理。赵倩等[8]和殷豪等[12]均表明EMD方法有助于改善模型预测性能,但未充分研究IMF分量对预测结果的影响,预测精度还有待改进。
EMD分解得到的高频分量振荡较为严重,对整体的预测精度影响较大,对预测模型的要求也较高。目前已有的研究中,基于HHT的预测大多是将各分量预测结果直接叠加[13],忽略了不同频率的IMF分量对预测结果的影响。因此,笔者提出权重浮动区间模型和数学解析模型2种权重优化方法以分析各IMF分量权重系数,进而建立了一种基于改进HHT的分钟级超短期风速预测模型,有效提高了原HHT组合预测模型的性能。
1 基于改进HHT的风速预测模型
1.1 希尔伯特黄变换
HHT是Huang等人于1998年提出的一种针对非线性、非平稳信号的处理方法[14],该方法易于实现,直观高效,具有自适应性、良好的时频聚集性、完备性及可重构性[15]。HHT理论由EMD和希尔伯特变换(HT)两部分组成。
EMD方法假设任何复杂信号均由简单的IMF组成,每个IMF分量都是相互独立的[16]。
对原始风速时间序列进行分解的具体过程如下:
(1) 识别信号v(t)的所有极大值点与极小值点,分别用三次样条函数拟合成原始风速时间序列的上、下包络线;
(2) 计算上下包络线的均值m1(t),用v(t)减去m1(t)得到h1(t);
(3) 若h1(t)满足IMF条件,记c1(t)=h1(t),则c1(t)为第一个IMF分量,为原始风速时间序列的最高频分量;否则,将h1(t)看作新的v(t),重复上述步骤k次,直到h1(t)满足IMF条件;
(4) 从原始信号中分离出c1(t),得到剩余分量:
r1(t)=v(t)-c1(t)
(1)
将r1(t)作为新的原始数据,重复上述步骤,得到n个IMF分量和1个剩余分量,结果如下:
(2)
当rn(t)满足给定的终止条件时,分解过程结束,原始风速时间序列可表示为:
(3)
式中:rn(t)为残余函数,代表信号的平均趋势;ci(t)代表信号不同时间特征尺度的成分,其尺度从c1(t)到cn(t)依次增大。
采用Huang等人提出的分量终止条件——类柯西收敛准则,即把连续2次IMF筛选序列结果的标准偏差系数(Standard Deviation,SD)作为评判标准[17],此处用Sd表示,定义如下:
(4)
式中:α为预先设置的足够小的数值,当Sd小于等于α时,筛选过程终止;T为原始风速时间序列的个数。
对于任意的时间序列X(t),Hilbert变换定义为X(t)与1/t的卷积Y(t):
(5)
式中:P为柯西主值,该变换对所有LP类均成立;τ为积分变量;t为当前时刻。
根据以上定义,可由X(t)与Y(t)得到复共轭解析信号Z(t):
Z(t)=X(t)+jY(t)=a(t)ejθ(t)
(6)
其中
(7)
此时,瞬时频率如下:
(8)
1.2 Elman神经网络
Elman神经网络在普通前馈式网络的基础上增加了层间的反馈连接,是一个动态反馈系统,由输入层、隐含层、承接层和输出层构成,其结构如图1所示。其中,输入层神经元用于传输信号,输出层神经元用于输出结果,承接层神经元从隐含层接收反馈信号,用来记忆隐含层神经元前一时刻的输出值,再反馈给隐含层。
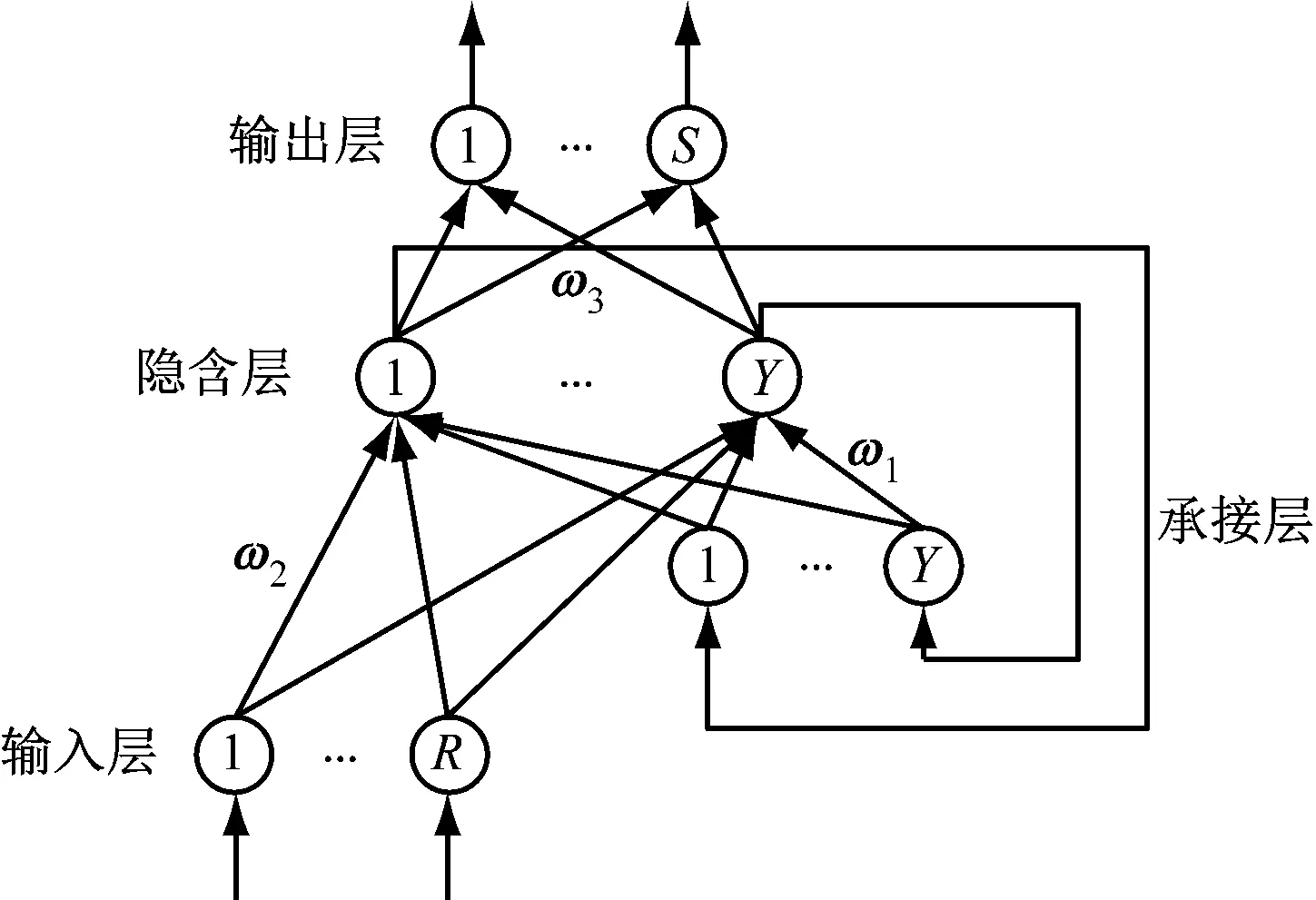
图1 Elman神经网络结构
Elman神经网络的输入输出关系如下:
y(t)=g(ω3x(t)+B2)
(9)
x(t)=f(ω1xc(t)+ω2u(t-1)+B1)
(10)
xc(t)=βxc(t-1)+x(t-1)
(11)
式中:u为R维输入向量;y为S维输出向量;x为Y维隐含层输出向量;xc为Y维承接层输出向量;ω1、ω2、ω3分别为承接层到隐含层、输入层到隐含层、隐含层到输出层的连接权值;B1、B2分别为隐含层与输出层的偏置;β为自连接反馈增益因子,当β为零时,为标准Elman网络,否则为修正的Elman网络,文中取β为零;g()为输出神经元传递函数,通常取线性函数;f()为隐含层神经元传递函数,通常取非线性函数。
为了提高预测精度,文中选取对数S型函数(logsig)和正切S型函数(tansig),表达式分别为:
(12)
(13)
Elman神经网络的学习算法采用梯度下降学习算法,其目标函数如下:
(14)
式中:Yk(t)和yk(t)分别为t时刻第k个输出神经元的期望输出和实际输出。
1.3 预测性能评价指标
为了更好地评估所建预测模型的性能,采用3种误差评估指标,分别为均方根误差eRMSE(Root Mean Square Error,RMSE)、平均绝对误差eMAE(Mean Absolute Error,MAE)和平均绝对百分比误差eMAPE(Mean Absolute Percentage Error,MAPE),其表达式[18]分别为:
(15)
(16)
(17)
1.4 权重优化模型
为求取各分量权重系数,提出权重浮动区间模型和数学解析模型2种方法。
1.4.1 权重浮动区间模型
权重浮动区间模型基于原HHT方法,旨在通过实验分析得到各分量权重系数,该方法实施简单。具体实施步骤如下:
(1) 参数初始化:初始状态即不考虑各分量影响时的模型,故设定循环计数为1,各分量权重为1,即权重向量Q=[1,1,…,1],向量维数等于分量个数;
(2) 计算出初始误差向量E,E=[eRMSEeMAEeMAPE];
(3) 设定权重浮动区间为[-0.1,0.1],从而随机生成权重增量Qs,该向量维数与Q一致;
(4) 求得新权重向量,即Qx=Q+Qs;
(5) 按新权重计算风速预测结果,进而求得新的误差向量M,M=[eRMSEeMAEeMAPE];
(6) 循环计数加1;
(7) 判断循环计数是否大于设定值,结果为真,则退出循环,输出最优权重、预测结果及最终误差值;否则,继续循环。为保证最优权重的质量,此处的设定值应取较大值。
(8) 比较新误差与初始误差,若三项误差都减小,则返回步骤(2)更新初始误差向量,继续循环;否则,返回步骤(3)继续循环。
详细计算流程如图2所示。经反复运行统计,单次运行时间介于0.16~0.3 s,满足预测要求。
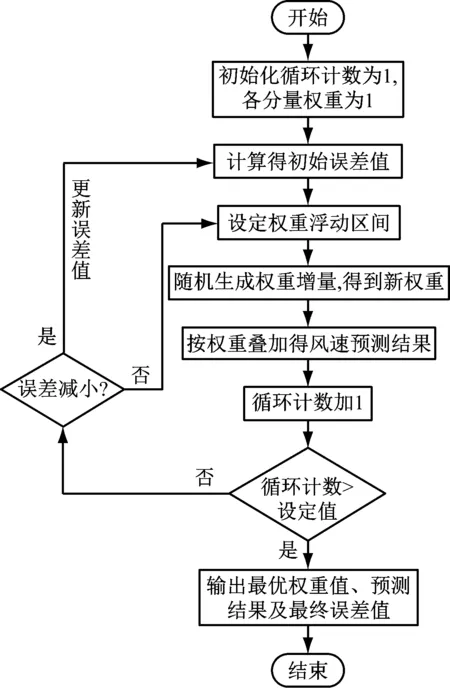
图2 权重浮动区间模型计算流程
1.4.2 数学解析模型
数学解析模型主要通过求解特定的数学模型来计算各分量权重系数,具体思路及求解过程如下:
按权重叠加的风速预测结果为:
(18)
式中:Q1,…,Qn,Qn+1为各分量所对应的权重系数;c1p(t),…,cnp(t),rnp(t)为各分量预测结果。
此处以均方根误差最小为目标函数[19],即
(19)
求解上式,等同于求解式(20),即误差平方和P最小:
(20)
将式(18)代入式(20)可得:
Qncnp(t)-Qn+1rnp(t))2
(21)
求P对各权重系数的偏导,使其满足以下约束条件,即可求得最优权重系数:
(22)
1.5 组合预测模型
建立了基于数据预处理与权重分配的组合预测模型。首先,基于数据预处理技术对原始风速时间序列进行EMD分解,得到一系列相对平稳的IMF分量和1个剩余分量。然后,对各分量依次进行Hilbert变换,针对其频谱特性,分别建立不同的Elman神经网络模型进行预测。最后,根据各分量预测结果,分别利用权重浮动区间模型和数学解析模型求取各分量权重系数,按权重叠加各分量预测结果,得到2组风速预测值,通过线性组合得到最终预测结果。由于权重浮动区间模型和数学解析模型各有特点,因此运用组合思想,以预测误差平方和最小为优化目标,采用滚动时间窗动态调整2组风速预测值线性组合的权重系数。时间窗的选取会影响权重数值的变化,分别将时间窗设置为6、10和14,发现当时间窗较大时,权重波动较小,但可能丢失信号的某些特征;当时间窗较小时,权重波动较大,分析得到的特征可能已经失去了实际意义,因此选取时间窗窗口大小为10。实际预测过程中,当前时刻的实际风速值未知,故用上一时刻求得的权重系数来计算当前时刻的预测风速值。详细预测流程如图3所示。
基本步骤如下:
(1) 对原始风速时间序列进行EMD分解。
(2) 对分解后的分量依次进行Hilbert变换,针对其频谱特性,分别建立不同的Elman神经网络模型进行预测。
(3) 建立权重浮动区间模型和数学解析模型2种权重优化模型。
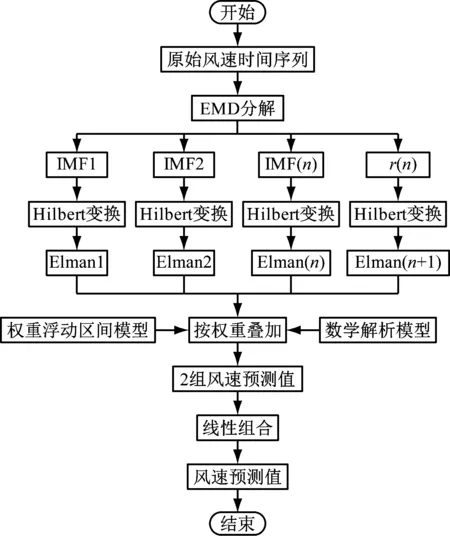
图3 组合预测流程图
(4) 利用上述2种模型分别求取各分量权重系数。
(5) 按最优权重线性组合2组预测结果,得到最终风速预测值。
2 算例及结果分析
选取中国陕西靖边风电场某风电机组2015-08-22—2015-09-04的实际运行数据进行算例分析。数据的时间分辨率为1 min,经数据清洗处理,取前1 200组作为实验样本,其中前1 164组为训练集,后36组为测试集。实验样本原始风速数据的统计指标见表1。

表1 原始风速数据的统计指标
原始风速数据及其EMD分解结果如图4所示,共分解出8个IMF分量和1个剩余分量。由图4可以明显看出IMF分量的时间特征尺度从IMF1到IMF8依次增大,其频率由高到低变化。
对各IMF分量的原始数据进行归一化处理,并建立各自的最佳Elman神经网络模型。为提高预测精度,用到2种线性归一化方法,分别如下:
(23)
(24)
式中:xi为原始数据x的第i个值;min( )、max( )、mean( )分别为最小值、最大值、平均值求取函数。
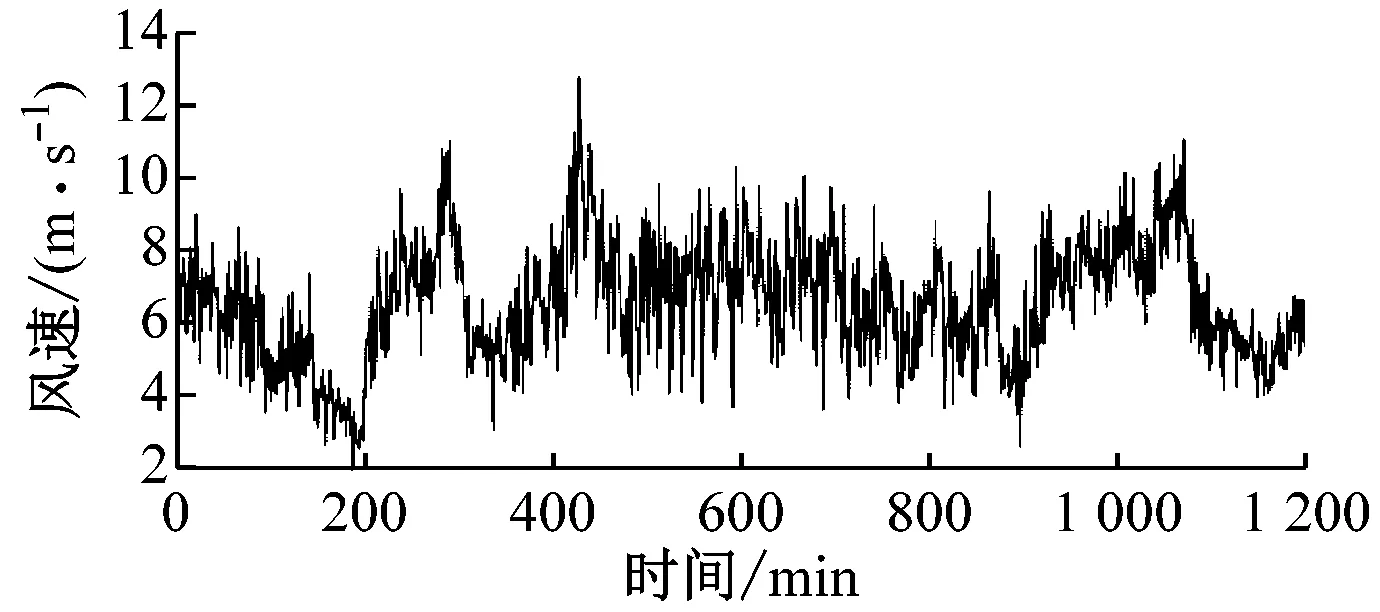
(a) 原始风速时间序列
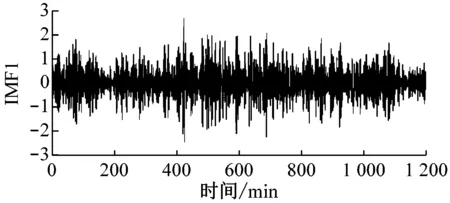
(b) IMF1
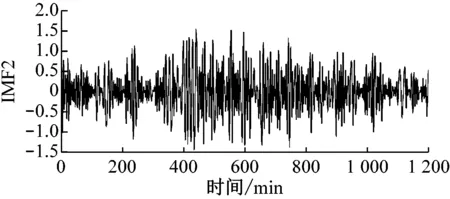
(c) IMF2
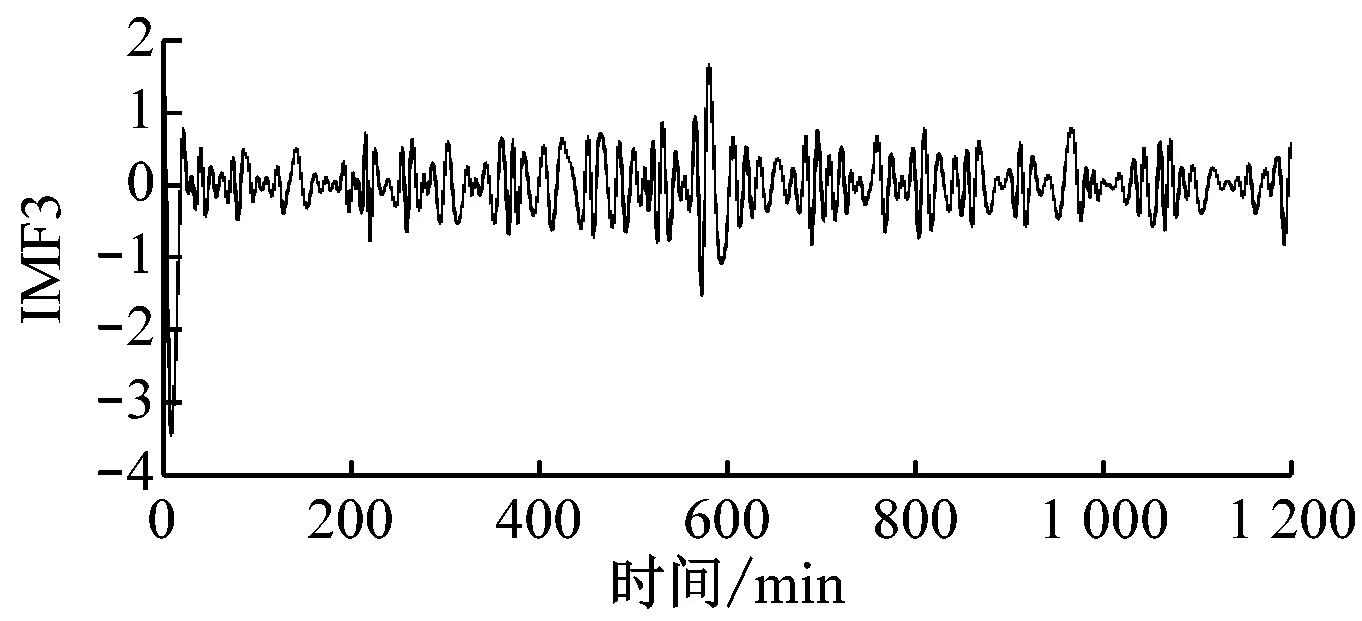
(d) IMF3
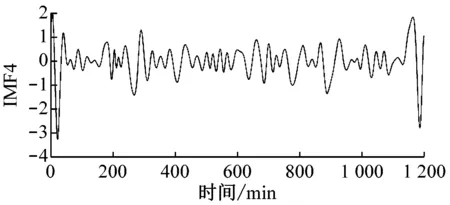
(e) IMF4
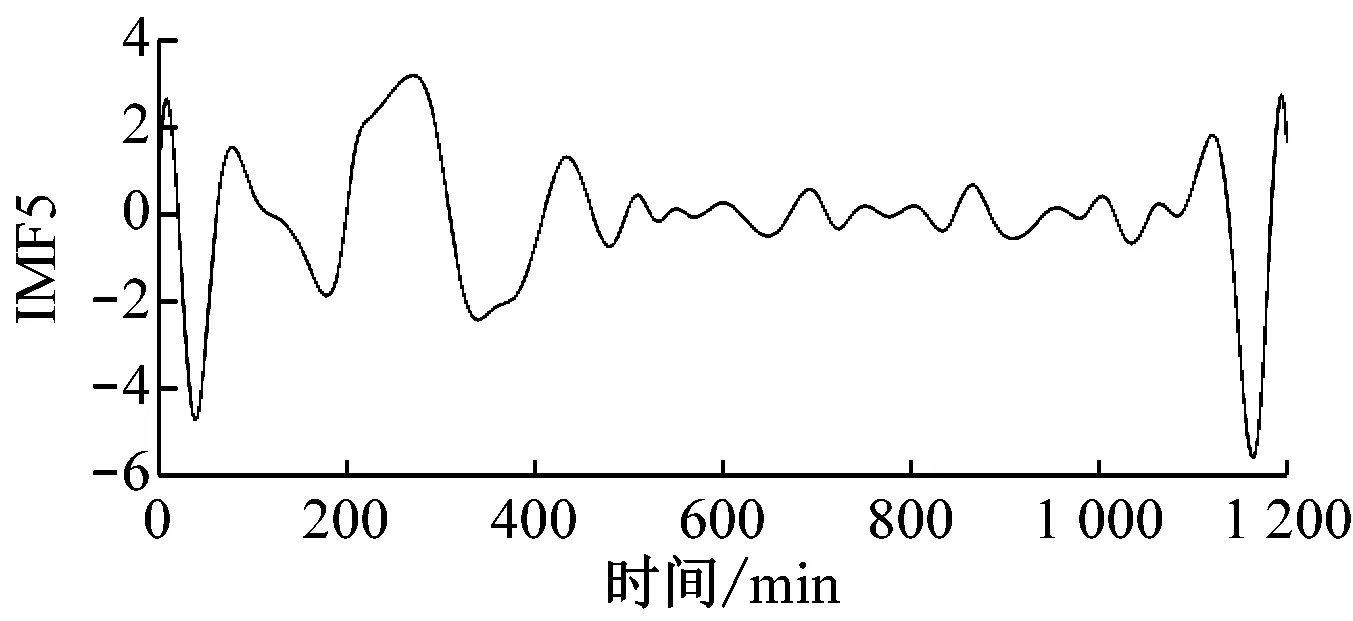
(f) IMF5
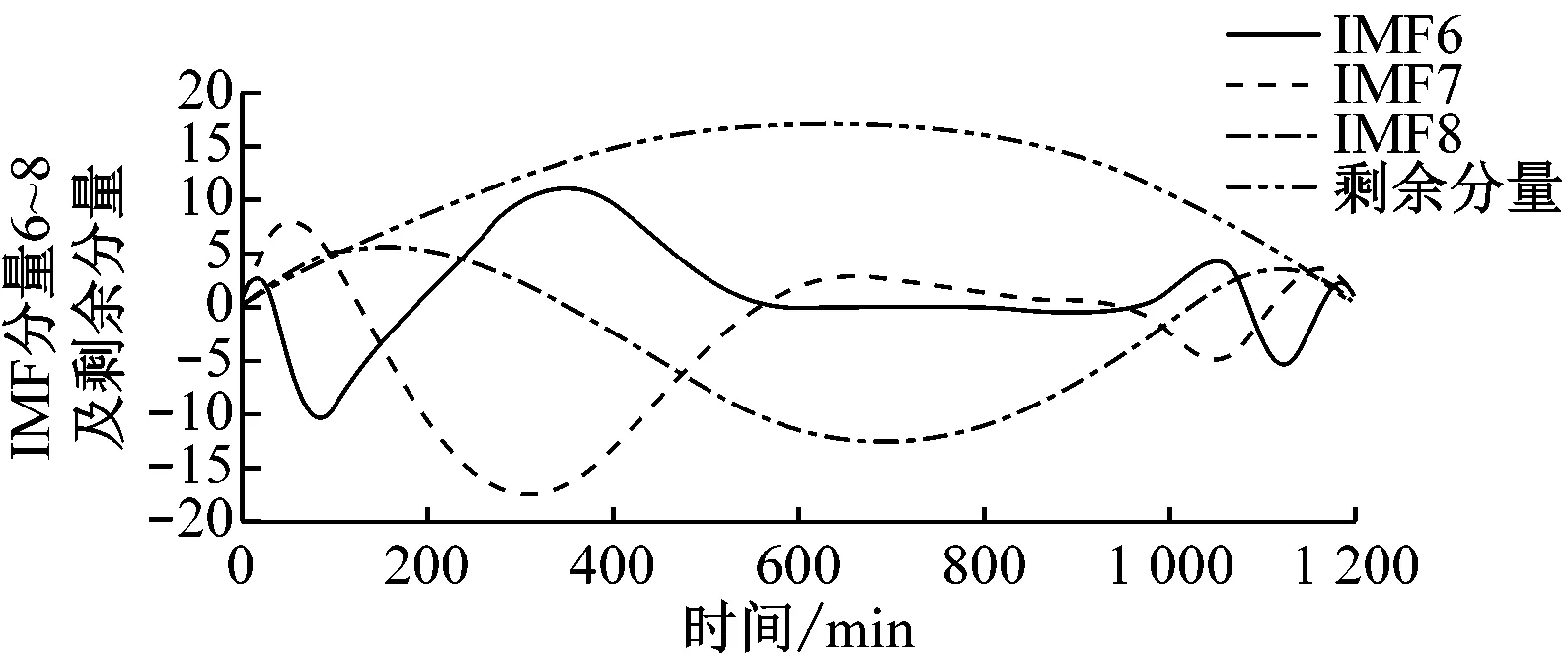
(g) IMF分量6~8及剩余分量
由式(23)可将数据归一化到[0,1],由式(24)可将数据归一化到[-1,1]。
为选取模型的输入特征,利用皮尔逊相关系数分析了各IMF分量与原始数据间的相关关系,并对与原始数据相关性最大的3个分量进行实验分析,结果见表2。综合考虑模型复杂度及训练耗时,本算例最终选取前12 min的风速数据作为网络的输入,对该机组的风速进行了提前1 min的滚动预测。
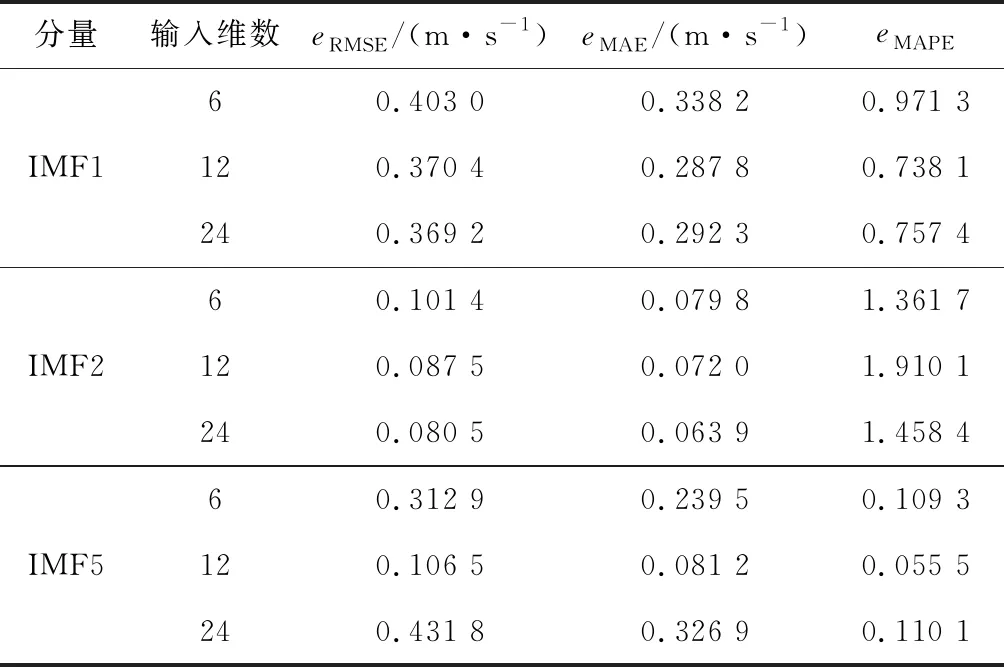
表2 输入特征选取实验结果
为了更好地验证所建模型的有效性,还对原始风速数据建立了单一的径向基函数(RBF)和Elman预测模型,预测结果对比如图5所示。
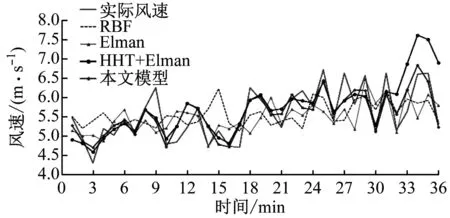
图5 实际风速及各模型的预测结果
由图5可见,单一的RBF预测效果较差,有一定的时间滞后现象,当风速变化较大时,往往很难追踪预测;单一的Elman预测效果较RBF略好一些,对风速数据的突变响应也存在滞后现象,但能够较准确地预测个别点。而基于HHT的Elman神经网络预测模型的预测效果整体有所提高,基本不存在滞后现象,但是也存在个别突变点误差较大的情况。相比之下,笔者所建立的基于改进HHT的组合预测模型的预测精度比原HHT组合预测模型有所提高。
各模型的误差评估结果见表3。从表3可以直观地看到本文所建模型的预测结果最优,其eRMSE、eMAE、eMAPE分别为0.364 4 m/s、0.287 0 m/s和5.14%,而单一RBF神经网络的eRMSE、eMAE和eMAPE分别为0.612 5 m/s、0.507 7 m/s和9.17%。此外,为了更客观地比较各模型的性能,表4给出了其误差改进情况。这表明通过HHT对随机性、非线性极强的原始风速数据进行分解,并结合权重优化算法求解各分量权重系数可有效提高预测精度,有一定的可行性。但是,本算例中分钟级的预测对象不局限于风电机组,后续工作中可以将其应用于风电场或风电集群预测,并考察多步预测。此外,文中所提权重浮动区间模型尚存在一定的局限,未来研究中将进一步优化模型,提高算法的鲁棒性。
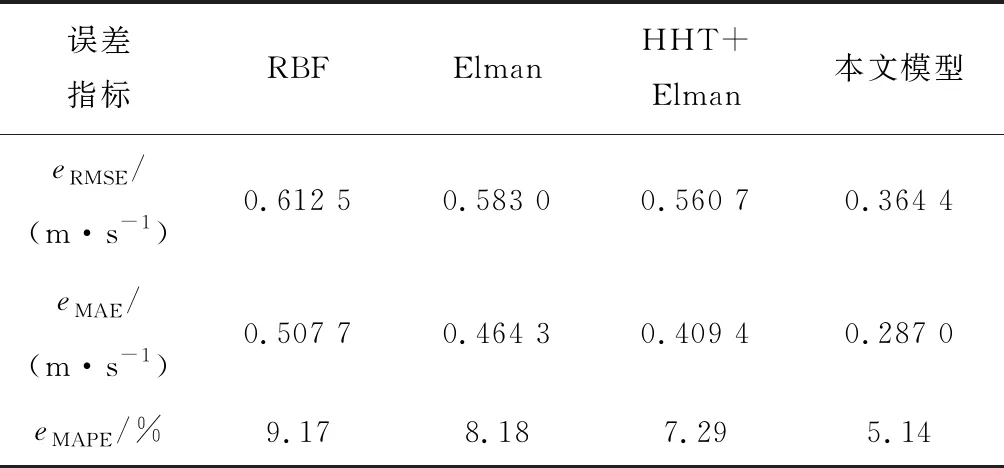
表3 不同预测模型的误差评估结果
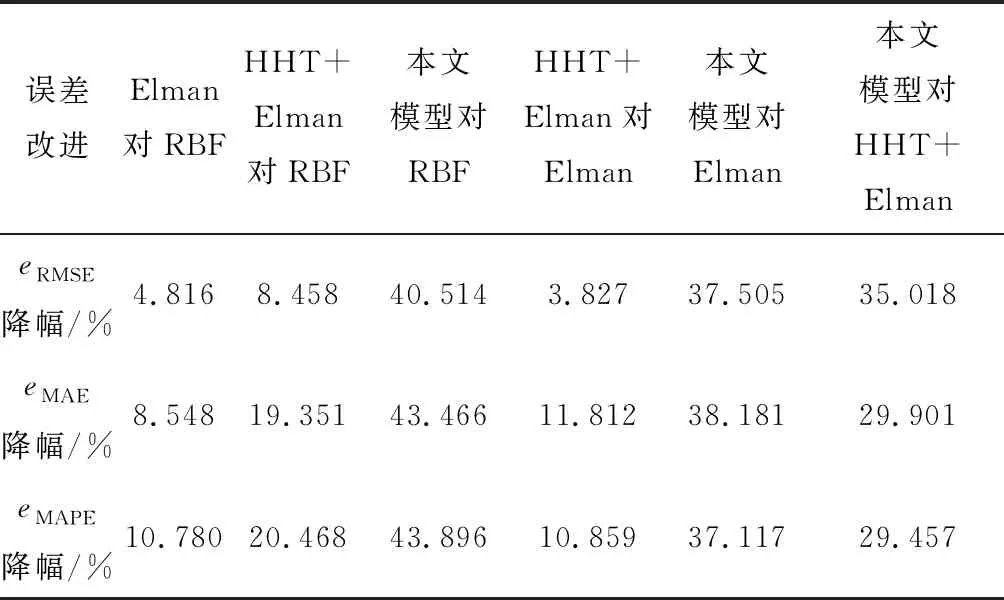
表4 不同预测模型的误差改进情况
3 结 论
(1) 利用HHT方法在处理非线性、非平稳性信号方面的优势,有效挖掘了风速固有的物理特性。
(2) EMD分解得到的分量对整体预测精度影响较大,通过权重浮动区间模型和数学解析模型分析各分量权重系数,从某种层面量化了这种影响。
(3) 所提出的基于数据预处理与权重分配的组合预测模型能有效改善原HHT组合预测模型的预测效果。
(4) 所建立的组合预测模型挖掘了风速本身的物理特性,可有效提高超短期风速预测的精度并应用于实际风速预测。
