关于夹芯梁四点弯曲试验的计算分析

吴 晓，刘奇元

(湖南文理学院 机械工程学院，湖南 常德 415000)

1 引 言

夹芯梁在航空航天、土木工程、家具产品等领域有着广泛的应用。文献[1]研究了新型混合芯材复合材料夹芯板受弯性能，文献[2]研究了基于Reissner理论的加强结构绝缘板(FSIP)挠度分析，文献[3]研究了格构腹板增强泡桐木夹芯复合板的弯曲性能，文献[4]研究了双向格构腹板增强泡沫夹层复合材料梁弯曲性能，文献[5]研究了格构腹板增强复合材料泡沫夹芯板侧压性能试验分析。

文献[1-5]在研究夹芯梁的弯曲挠度时，均采用经典方法来计算夹芯梁中点挠度，但经典方法的计算精度不是很高。文献[6]采用有限元方法研究了泡沫铝/铸铁层合梁的弯曲性能，文献[7]把夹芯梁四点弯曲实验引入到材料力学试验研究性教学中，采用材料力学方法计算了夹芯梁中点截面应力。基于以上因素，本文修正了夹芯梁弯曲应力公式及弯曲挠度公式。

2 夹芯梁的弯曲应力及挠度

夹芯梁横截面及梁微段受力示意图如图1所示。

图1 夹芯梁横截面及微段示意图

由材料力学可知，夹芯梁表面板内剪应力表达式为：

(1)

式中：

D为夹芯梁弯曲刚度，E1、E2分别为夹芯梁表面板、夹芯层的弹性模量，Q为梁横截面剪力，h为夹芯层高度，t为表面板厚度，b为梁宽度，z为梁截面表面板任意点至中性层的距离。

材料力学给出了夹芯梁在没有考虑剪切效应时表面板及夹芯层的弯曲正应力公式，分别为：

(2)

式中，M(x)为梁截面弯矩。

利用式(2)可得到图1所示梁微段左侧轴向拉力为：

(3)

同理，利用式(2)可求得图1所示梁微段右侧轴向拉力为：

(4)

梁微段轴向静力平衡方程为：

N1+τ2bdx=N2

(5)

把式(3)、式(4)代入式(5)，可求得夹芯层截面剪应力表达式为：

(6)

由弹性力学可知，轴向位移、横向位移与剪应力、剪应变的关系为：

(7)

式中，ui为轴向位移，wi为横向位移，γi为剪应变，Gi为剪切弹性模量，i=1时代表上、下表板，i=2时代表夹芯层(以下类同)。

把式(7)对z积一次分可得：

(8)

式中，ki为待定常数。

夹芯梁表板与夹芯层连接处、中性轴处位移条件为：

z=0,u2=0

(9)

把式(1)、式(6)代入式(8)且利用式(9)可得：

(10)

(11)

夹芯梁横截面弯矩平衡方程为：

(12)

把式(11)代入式(12)中，可得夹芯梁弯曲微分方程为：

(13)

式中：

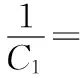
C为梁的剪切刚度，C1为表板产生的剪切刚度，C2为夹芯层产生的剪切刚度。

把式(13)代入到式(11)中，即为夹芯梁弯曲正应力公式。

3 理论公式计算精度

下面以图2所示均布载荷作用下各向同性材料简支梁为例，把下文方法计算结果与弹性理论计算结果进行对比。

图2 均布载荷作用下简支梁

令q(x)=q，E1=E2=E，G1=G2=G，t=0，由式(11)可以求出图2所示简支梁横截面弯曲正应力为：

(14)

由式(13)可以求出图2所示简支梁中点挠度为：

(15)

利用E=2(1+μ)G，参考文献[8]，令μ=0.25，可知图2所示简支梁中点最大正应力及挠度分别为：

(16)

(17)

文献[9]给出μ=0.25时图2所示简支梁中点最大正应力及挠度的弹性解分别为：

(18)

(19)

下面把式(16)、式(18)的计算结果列在表1中，把式(17)、式(19)的计算结果列在表2中，以便比较分析。

表1 最大弯曲正应力

表2 梁中点挠度

从表1、表2可以看出，本文方法计算的结果与弹性解的计算结果非常接近，即使长高比l/h=2时，应力、挠度的误差也仅为1.5%、3.23%。可以看出，本文方法计算精度非常高。

文献[7]把夹芯梁弯曲试验引入到材料力学实验教学中，文献[7]给出了图3所示夹芯梁中点横截面弯曲正应力公式，但没有给出图3所示夹芯梁中点挠度表达式。

图3 四点弯曲夹芯梁

利用式(3)，可以方便地求出图3所示夹芯梁中点挠度为：

(20)

文献[8]采用四点弯曲试验研究了泡桐木夹层结构材料力学性能。夹层梁上、下面板厚均为2.4mm，泡桐木夹芯厚度为38mm，梁宽为80mm，梁长l=450mm，加载点间距a=150mm。面板弹性模量为209MPa。图3所示泡桐木夹层梁的文献[8]试验值与式(20)的计算结果列在表3中。

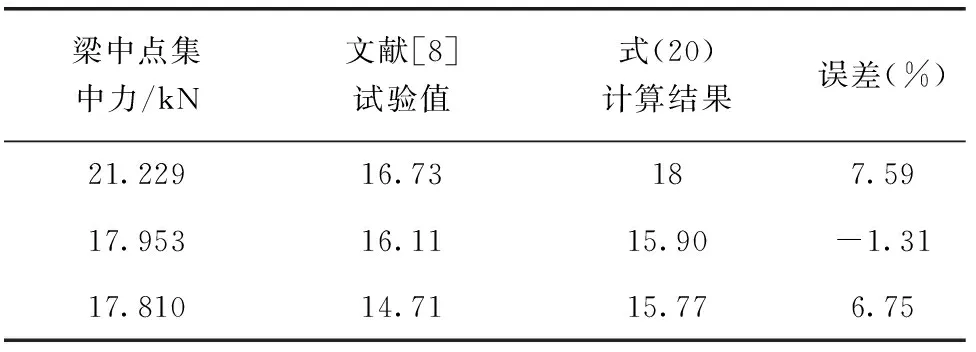
表3 四点弯曲梁中点挠度(mm)

由表3可以看出，式(20)计算结果与文献[8]的试验值吻合得较好。

另外，由以上计算及式(11)可以看出，均布载荷作用下，剪切变形对梁的弯曲正应力及弯曲挠度都有影响。由以上计算及式(11)、式(13)可以看出，在集中力作用下，剪切变形仅对梁弯曲挠度有影响，而对梁的弯曲正应力没有影响。

4 四点弯曲夹芯梁的强度校核

文献[7]把夹芯梁四点弯曲试验引入材料力学实验研究性教学中，对培养学生的创新能力大有益处。

在实际工程应用中，夹芯梁面板与夹芯容易发生剥离，所以，为了保证夹芯梁面板与夹芯尽量不发生剥离，应对夹芯梁B点截面左边或C点截面右边，在面板与夹芯结合部采用第三强度理论或第四强度理论进行强度校核。

由文献[7]可知，图3所示四点弯曲夹芯梁的计算参数为：E1=210GPa，μ1=0.3，E2=14.9GPa，μ2=0.33，t=15mm，h=30mm，b=30mm，l=550mm，a=250mm，P=5kN。

利用式(6)可求得图3所示夹芯梁B点截面左边面板与夹芯结合部的剪应力为：

(21)

利用式(11)可求得图3所示夹芯梁B点截面左边面板与夹芯结合处的正应力为：

(22)

因此，由第三强度理论可知：

由第四强度理论可知

由以上应力计算可以看出，夹芯梁面板与夹芯梁结合部剪应力远大于弯曲正应力，所以应对夹芯梁面板与夹芯梁结合处采用强度理论进行强度校核。

由以上分析，本文有两点建议：

(1)在材料力学实验教学中，可以把夹芯梁四点弯曲试验作为一个创新试验，即在集中力作用点测试夹芯梁面板与夹芯梁结合处的正应力，然后采用强度理论进行强度校核，这样可以强化学生对强度理论教学内容的掌握。

(2)利用夹芯梁四点弯曲试验测试夹芯梁中点挠度，这样可以强化学生对梁弯曲变形教学内容的掌握。

本文关于矩形截面夹芯梁弯曲应力的计算方法，对齿板-玻璃纤维混合夹层梁、泡沫铝夹芯梁、泡桐木夹层梁等其它夹芯梁弯曲应力计算都适用。所以，本文关于夹芯梁计算方法对实际工程中有关设计人员也是有理论指导意义的。

5 结论及建议

(1)外载荷作用下夹芯梁四点弯曲时，在外载荷作用处夹芯梁面板与芯材结合部位应采用强度理论进行校核。

(2)均布载荷作用下剪切变形对梁的弯曲正应力及挠度都有影响，集中力作用下剪切变形仅对梁弯曲挠度有影响，而对梁的弯曲正应力没有影响。

(3)建议把夹芯梁四点弯曲试验改为在集中力作用处测试夹芯梁面板与夹芯层结合部的正应力，以便采用强度理论进行强度校核，同时在夹芯梁四点弯曲试验中测试夹芯梁中点挠度。