基于DSCNN-BiLSTM的入侵检测方法

商富博, 韩忠华,2*, 林 硕,2, 单 丹, 戚爰伟

(1.沈阳建筑大学信息与控制工程学院， 沈阳 110168； 2.中国科学院沈阳自动化研究所数字工厂研究室， 沈阳 110016)

随着互联网时代的到来，网络安全问题显得尤为重要，大量的网络流量数据导致网络环境面临着巨大威胁，一旦遭受黑客的恶意攻击，将会给人们的日常生活乃至国家安全带来隐患。入侵检测技术能够保障网络安全，近年来受到学术科研领域的广泛关注，其通过建立入侵检测模型，学习网络流量数据的特征信息，从而准确识别未知的攻击行为。

在入侵检测技术的研究中，文献[1]提出了一种基于异卷积神经网络的入侵检测方法，采用两种不同的卷积神经网络提取网络训练数据，从而得到最优模型，结果表明该方法具有良好的性能，但该方法的缺点是模型容易陷入过拟合[1]；文献[2]提出了基于相关信息熵和融合卷积神经网络和双向长短期记忆网络(CNN-BiLSTM)的工业控制系统入侵检测模型，将基于相关信息熵的特征选择和深度学习算法相结合，提高了检测精度，此方法的缺点为训练时间较长，模型结构较复杂[2]；文献[3]提出了一种基于深度卷积神经网络的入侵检测研究，可以自动从数据中提取局部特征，与已有的方法相比，所提方法具有更快的检测准确率、更低的误报率和更快的检测速率，但是该方法仅考虑网络流量数据的空间特征，忽略了网络流量数据的时间特征[3]；文献[4]提出了一种融合卷积神经网络(CNN)与双向长短期记忆网络(BiLSTM)的网络入侵检测方法，分别使用CNN模型、BiLSTM模型提取局部特征和长距离依赖特征，与单独使用CNN和BiLSTM相比，该方法的准确率较高，误报率较低，但该方法的模型参数较多，模型易陷入局部最优[4]。

现设计一种融合深度可分离卷积神经网络(DSCNN)和双向长短期记忆网络(BiLSTM)的DSCNN-BiLSTM模型[5]，提出了一种基于DSCNN-BiLSTM的入侵检测方法，使用主成分分析法(PCA)对网络流量数据进行特征选择，并创新性地将一维网络流量数据转化为三维图像数据作为模型的输入[6]，利用深度可分离卷积神经网络(DSCNN)提取网络流量数据的空间特征，将空间特征在时间上排列后，利用双向长短期记忆网络(BiLSTM)挖掘网络流量数据的时间特征，与其他入侵检测方法相比，DSCNN-BiLSTM方法较轻量化，计算量低，具有较强的学习能力，大大提高了入侵检测的性能。

1 相关工作

1.1 主成分分析法

网络流量数据的特点是维数高、关联性强，这会增加模型的训练时间，因此，需要对网络流量数据进行特征降维，降低后续数据建模和处理的复杂度。

主成分分析法(PCA)是机器学习中最常用的线性降维方法，其通过投影变换将原始高维数据映射到低维子空间，在尽可能保留样本方差的同时降低初始数据的维数[7]，可以将许多高度相关的特征转换为独立或不相关的特征，变换后的特征子空间包含绝大多数原始高维数据的特征，即

(1)

式(1)中：X为原始数据集；x11，x12,…，xnp为特征值。

主成分分析的计算步骤：

第一步计算样本相关系数矩阵：

(2)

式(2)中：R为相关系数矩阵；r11，r12,…，rpp为相关系数。为方便，假定原始数据标准化后仍用式X表示，则经标准化处理后数据的相关系数为

(3)

第二步用雅克比方法求相关系数矩阵R的特征值(λ1，λ2，…，λp)和相应的特征向量ai=(ai1,ai2,…，aip)。

第三步选择重要的主成分，并写出主成分表达式。

主成分分析可以得到p个主成分，但是，由于各个主成分的方差是递减的，包含的信息量也是递减的，所以实际分析时，一般不选取p个主成分，而是根据各个主成分[8]累计贡献率的大小选取前k个主成分。这里贡献率就是指某个主成分的方差占全部方差的比重，即

(4)

式(4)中：λ1，λ2，…，λp为相关系数矩阵的特征值；g为贡献率，g越大，说明该主成分所包含的原始变量的信息越强，主成分个数k的选取，主要根据主成分的累积贡献率来决定，即一般要求累计贡献率达到95%以上，这样才能保证变换后的数据包含原始数据的绝大多数信息，达到对网络流量数据降维的目的。

1.2 深度可分离卷积

近年来，深度可分离卷积被广泛应用于最新的深度神经网络中，逐渐取代了传统的标准卷积。标准卷积是对所有的通道共同实现卷积运算，而深度可分离卷积将标准卷积分解为逐深度卷积和逐点卷积，不仅涉及空间维度，还涉及通道维度[9]，其中逐深度卷积对每个输入信道独立执行空间卷积，实现网络流量数据的空间特征提取，然后使用逐点卷积对逐深度卷积提取出的空间特征进行融合，这种深度可分离卷积结构能够降低模型的复杂度，减小模型的参数和计算量，优化模型速度。

设卷积层的输入特征图为I,大小为H×W×C，其中H为特征图的长度,W为特征图的宽，C为特征图的通道数；卷积核为M，大小为K×K×C×N，其中K为卷积核的大小，N为卷积层的输出特征图通道数[10]；输出的特征图为O，大小为H′×W′×N，其中H′和W′分别为输出特征图的高和宽，根据标准卷积的定义，可得

(5)

标准卷积参数数量为

x1=K×K×N×C

(6)

计算量为

y1=K×K×C×N×H′×W′

(7)

而与标准卷积不同，深度可分离卷积每一个卷积核分别对应一个通道，可分离卷积可表述为

(8)

深度可分离卷积参数数量为

x2=K×K×C+1×1×C×N

(9)

计算量为

y2=K×K×H′×W′×C+C×H′×W′×N

(10)

相比标准卷积，深度可分离卷积减小了模型的参数和计算量，使得模型轻量化。可对比二者的参数数量比，即

(11)

可对比二者的计算量比，即

(12)

由式(11)和式(12)可见，当卷积核大小为3×3时，深度可分离卷积的参数数量和计算成本大约为标准卷积的1/9，模型明显轻量化，能够大大提高模型的训练速度[11]。

1.3 双向长短期记忆网络(BiLSTM)

相比长短期记忆网络(LSTM),双向长短期记忆网络(BiLSTM)是长短期记忆网络(LSTM)的一种变体，能够提取长距离依赖信息的特征，充分考虑前后特征之间影响。在单向LSTM中，信息由前向后流动，而在双向LSTM中，包含一个前向LSTM层和一个后向LSTM层，一个从左到右处理时间特征，另一个从右到左处理时间特征，因此，BiLSTM能够更好地捕捉前后特征之间的关联性，得到更加全面的特征信息[12]。

设BiLSTM的输入特征向量为x，在每一个时间步上，由三个门来控制细胞状态，分别为输入门it、输出门ot和忘记门ft。BiLSTM的第一步是通过忘记门ft来决定细胞需要舍弃哪些特征信息，通过前一个时间步的输出ht-1和当前时间步的输入xt计算ft；第二步是通过输入门决定给细胞状态添加哪些特征信息[13]，利用ht-1和xt通过一个tanh激活函数得到候选的细胞信息cnt，然后通过忘记门ft舍弃一部分细胞信息并添加cnt得到新的细胞信息ct；第三步根据ht-1和xt来判断输出细胞的哪些特征信息，此时需将输入经过输出门输出得到一个0～1的数，然后将细胞状态经过一个tanh激活函数得到一个-1～1值的特征向量，该特征向量与经输出门得到的数相乘得到此时间步的输出。在此时间步t上，利用 BiLSTM 模型的正向和反向部分对X进行特征提取，前向LSTM具体实现为

(13)

后向LSTM具体实现为

(14)

式中：σ为sigmoid激活函数；tanh为双曲正切函数；bt为时间步的输出；wi、wf、wc、wo分别为输入门权值、忘记门权值、候选细胞权值和输出门权值；bi、bf、bc、bo分别为输入门偏置、忘记门偏置、候选细胞偏置和输出门偏置。经过BiLSTM双向特征提取得到输出的特征向量，能够考虑到网络流量数据前后特征之间的相关性，从而提高入侵检测的识别准确率[14]。

2 基于DSCNN-BiLSTM的入侵检测方法

提出一个基于DSCNN-BiLSTM的入侵检测方法，将深度学习应用到入侵检测技术中，该方法的整体流程如图1所示，主要包括五部分:①数据的预处理，包括数据的数值化处理和数据的归一化处理，其能够有效解决数据样本不同特征取值范围不同的问题[15];②数据的特征选择，由于网络流量数据之间存在着高度的相关性，故运用主成分分析法对高维的数据进行特征降维，可以减少数据集的冗余度;③数据的图像化处理，将一维的网络流量数据转换为三维图像作为模型的输入;④构建DSCNN-BiLSTM模型;⑤使用KDDCUP99网络流量数据集进行训练、验证和测试[16]。

图1 基于DSCNN-BiLSTM的入侵检测方法流程图Fig.1 Intrusion detection method flow chart based on DSCNN-BiLSTM

2.1 数据的数值化处理

KDDCUP99数据集包含约500万条网络流量数据，是入侵检测领域公认的数据集，选用其中10%的子集作为本文的入侵检测数据。数据集每个样本包含41个特征，共分为四类：TCP连接的基本特征共9种、TCP连接的内容特征共13种、基于时间的网络流量统计特征共9种和基于主机的网络流量统计特征共10种。每个样本被标记为“正常类型”或“攻击类型”，这些攻击类型可分为四类：拒绝服务攻击(DOS)、远程到本地的未授权访问(R2L)、未授权的本地超级用户特权访问(U2R)和端口监视(PROBING)[17]。

KDDCUP99数据集中protocol_tpye、service和flag这三个特征为字符型特征，而模型无法有效处理字符型特征，需将字符型特征做数值化处理。例如，protocol_tpye特征有三个值，分别为tcp、udp和icmp，应用one-hot编码后，其值分别为[1,0,0]、[0,1,0]和[0,0,1]，对service和flag这两个特征作同样的处理，42列的数据集扩展成为122列，其中最后一列为样本标记值[18]。

对五种样本标记值Normal、DOS、R2L、U2R和PROBING进行编号，分别为0、1、2、3和4，便于在后续的训练、验证和测试中对标记值进行one-hot编码。

2.2 数据的归一化处理

经过数值化处理的网络流量数据所有特征均为数值型特征，但是不同特征之间差异较大。例如第8个特征wrong_fragment，其值介于0～3， 而第16个特征num_root，其值介于0～7 468，这将促使模型认为第16个特征比第8个特征重要的多，而实际情况可能并非如此，这将会影响模型的训练效果，必须对网络流量数据进行归一化处理，本文采用z-score标准化方法，将数据集中的数据归一化到[-1,1]区间之内，标准公式为[19]

(15)

2.3 PCA特征降维

网络流量数据维度之间存在着冗余，且各个维度之间具有一定的相关性，这大大降低入侵检测模型的训练时间，影响训练效果，因此，需对高维的网络流量数据进行特征降维，以此减少数据集的冗余度，提高模型的检测性能。

通过上文的预处理后，网络流量数据的维度为122维，最后一维为样本标记值，对网络流量数据的前121维运用主成分分析法(PCA)进行特征降维，得到的累积贡献率如图2所示[20]。

图2 累积贡献率Fig.2 Cumulative contribution rate

由图2可以看出，前90个主成分可以代表99%的网络流量数据，因此，要想在PCA特征降维后依旧保留原始数据集的大部分有效信息，应选取的输入维度为90～121，现选取108作为特征降维后的数据维度。

2.4 数据的图像化处理

经过上述处理，网络流量数据为由108个有效特征组成的降维数据集，为了更好地提取网络流量数据的特征信息，将一维度的网络流量数据构造成6×6×3的三维图像作为DSCNN-BiLSTM模型的输入，利用深度可分离卷积神经网络(DSCNN)提取网络流量数据的空间特征信息，将所学到的特征输入双向长短期记忆网络(BiLSTM)，用于挖掘网络流量数据的时间特征，由于输入的三维图像数据通道值为3，分别代表红绿蓝(RGB)，三个颜色通道分别有不同的像素值(网络流量数据的特征值)，通过三个颜色通道相互之间的叠加来得到各式各样的颜色，从而创新性的将一维网络流量数据转化为三维图像数据作为模型的原始输入，从而更好地提取网络流量数据的空间特征，在数据集的五种样本类型中，各选取一个随机样本转换成三维图像之后的可视化图像如图3所示。

图3 转换后的三维图像数据Fig.3 Converted 3D image data

2.5 DSCNN-BiLSTM模型

近年来，深度可分离卷积神经网络(DSCNN)被广泛用于三维图像的特征提取，其对输入的每个通道进行独立的空间卷积，然后通过逐点卷积将输出通道混合，其不仅涉及空间维度，还涉及通道维度，使得参数和运算的数量得以减少，从而得到性能更好的模型，实现对网络流量数据的空间特征提取；而双向长短期记忆网络(BiLSTM)能够利用其顺序敏感性的优势，充分考虑前后特征之间的影响，挖掘网络流量数据的时间特征。

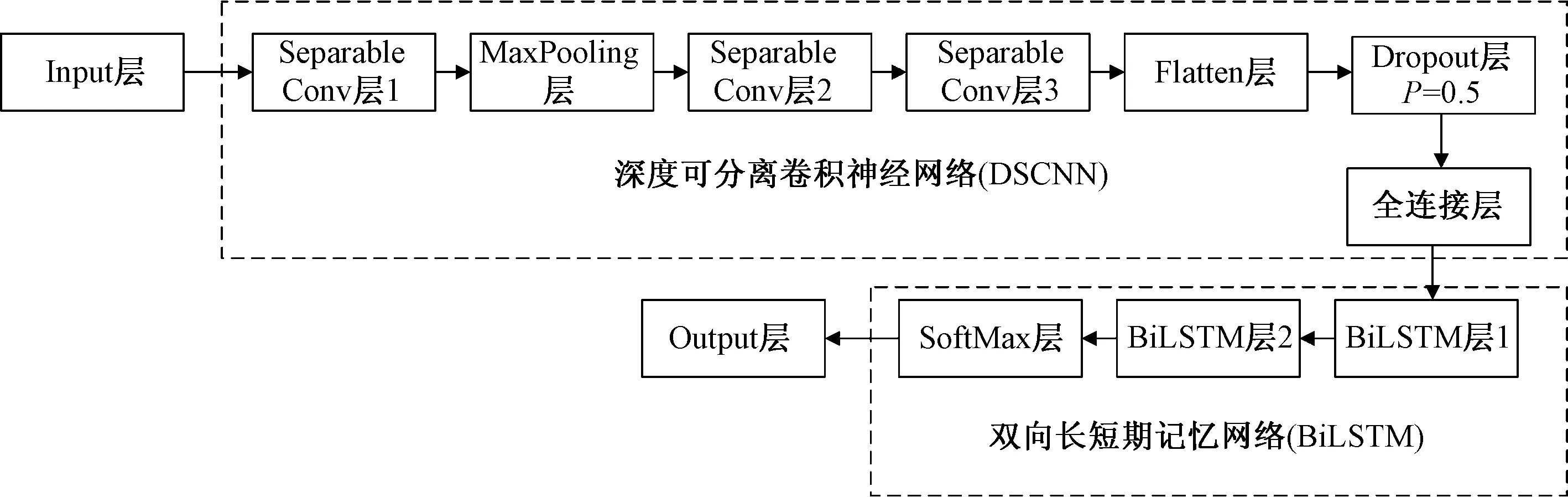
图4 DSCNN-BiLSTM模型结构图Fig.4 Structure diagram of DSCNN-BiLSTM model

融合DSCNN和BiLSTM的入侵检测模型针对网络流量数据具有空间和时间的双重特征实现对网络流量数据的特征提取，模型的结构如图4所示。

DSCNN-BiLSTM模型的第1层为输入层，网络流量数据经过图像化处理后，转化成为6×6×3的图像数据作为模型的输入。

第2层、第4层和第5层为卷积层，使用深度可分离卷积代替标准卷积，卷积核大小均为3×3，第2层步长为2，第4层和第5层步长为1，分别选取8、16和32种过滤器，输入图像数据大小6×6×3，通道数量为3，而在几次卷积运算之后，图像数据可以有多个通道，每个通道具有不同的特征信息，通过逐深度卷积对每个通道单独进行空间特征提取，再通过逐点卷积实现特征融合，实现了通道内卷积与通道间卷积的分离，从而在保证较高准确率的前提下减少模型参数和计算量，加快模型的收敛和训练速度，且在每个卷积层后使用BN方法，用来防止模型出现过拟合，提升模型的泛化能力。

第3层为池化层，池化能起到下采样的作用，从而简化网络结构，减少网络参数，为增加网络深度留下余地。

第6层为Flatten层，其将提取到的三维空间特征一维化，大小为64维；第7层为Dropout层，在模型训练时，按照概率0.5随机将网络中的某些神经元丢弃掉，从而防止模型出现过拟合；第8层为全连接层，运用Reshape函数将提取到的空间特征转化为1×64维的特征向量，将其作为双向长短期记忆网络(BiLSTM)的输入；第9层和第10层为BiLSTM层，针对双向长短期记忆网络(BiLSTM)容易遇到性能瓶颈的问题，使用循环层堆叠的方法增大网络容量，从而提升模型的检测性能；第11层为SoftMax层，用于分类预测；最后一层为模型的输出层，输出模型的分类预测结果。

3 仿真实验

3.1 实验数据集与仿真环境

选用10%的KDDCUP99数据集作为本文的入侵检测数据，训练集、验证集和测试集的比例为6∶2∶2，其中训练集用于模型训练，验证集用于模型参数调优，测试集用于进行入侵检测测试，实验数据如表1所示。

为了验证入侵检测模型的检测效果，搭建仿真环境，实验的配置环境如表2所示。

表1 数据集信息Table 1 Dataset information

表2 实验环境配置Table 2 Experimental environment configuration

3.2 评价指标

入侵检测模型的评价指标，主要包括准确率(ACC)、查准率(P)、漏报率(FNR)所有这些评价指标都派生自混淆矩阵(表 3)中的四个值。

TP：实际值为1，预测值为1，结果正确。

FP：实际值为0，预测值为1，结果错误。

FN：实际值为1，预测值为0，结果错误。

TN：实际值为0，预测值为0，结果正确。

表3 混淆矩阵Table 3 Confusion matrix

(16)

(17)

(18)

3.3 模型结构

经过数据的图像化处理，一维的网络流量数据已经转化为6×6×3的三维图像数据，将其作为入侵检测模型的输入，故模型的输入层维度为6×6×3；由于入侵检测数据共有5种类型，分别为Normal、DOS、R2L、U2R和PROBING，并分别编号为0、1、2、3和4，应用one-hot编码，分别转换为[1,0,0,0,0]、[0,1,0,0,0]、[0,0,1,0,0]、[0,0,0,1,0]和[0,0,0,0,1]，故模型的输出层设置为5，模型结构如表4所示。

表4 模型各层参数Table 4 Parameters of each layer of the model

3.4 超参数设置分析

在模型训练前，要进行超参数的设置，而不同的超参数会影响模型的训练效果，为了寻找相对最优的超参数，针对模型的激活函数、优化算法和学习率等超参数，作了对比实验。

图5 超参数对比实验Fig.5 Superparametric comparative experiment

激活函数的主要作用是为模型增加非线性映射学习能力，sigmoid、relu和tanh等为深度学习中常见的激活函数，在保证其他参数一致的情况下，进行对比实验，实验的对比效果如图5(a)所示,可以看出，在模型稳定后，relu函数的训练准确率大于sigmoid函数和tanh函数，因此，relu激活函数的学习效果最好，故选取relu函数作为模型的激活函数。

在深度学习的领域，常见的优化算法有SGD,Adam和RMSPROP等，其中SGD算法保持单一的学习率更新所有权重，学习率在网络训练过程中并不会改变; RMSProp算法对梯度计算了微分平方加权平均数,有利于解决训练过程中上下波动较大的问题;而Adam算法通过计算梯度的一阶矩估计和二阶矩估计为不同的参数设计独立的自适应性学习率，运用这三种优化算法分别进行模型训练，训练的效果如图5(b)所示,SGD算法的训练准确率较低，Adam算法的性能相对最优，故选择Adam算法作为本模型的优化算法。

学习率的设置在模型训练中至关重要，学习率设置的过大，会导致梯度在最小值附近来回浮动，使得模型无法收敛到最优；而学习率设置的过小，模型收敛速度将会变慢，且容易陷入局部最优，所以说，选择一个合适的学习率，对于模型训练来说，显得尤为重要，现通过设置不同的学习率进行对比实验，将模型的训练精度作为评价指标，对比效果如图5(c)所示,当学习率为0.001时，训练效果最好，故设置模型的学习率为0.001。

3.5 实验结果与分析

本文应用的10%KDDCUP99数据集有五种数据类型，故本文中是五分类实验，选取交叉熵损失函数(categorical_crossentropy)作为模型的代价函数，采用relu损失函数作为模型的激活函数，设置学习率为0.001，应用Adam优化算法是实现反向传播训练。

迭代次数和训练准确率的关系曲线如图6(a)所示，迭代次数和损失值的关系曲线如图6(b)所示，观察两组图像可知，模型训练时，训练精度逐步上升最后趋于稳定，损失值呈现稳定下降的趋势，最后趋近于0，可以得出模型具有良好得训练效果，已经收敛到了最佳状态。

为了验证本文中提出的基于DSCNN-BiLSTM的入侵检测方法的优势，将DSCNN-BiLSTM方法与CNN方法和LSTM方法进行对比，三种方法的迭代训练效果如图7所示。

由图7所示，CNN、LSTM和DSCNN-BiLSTM方法在15次迭代后均趋于稳定，训练精度都在98%以上，DSCNN-BiLSTM方法的训练精度明显好于CNN和LSTM。然后将本文方法与传统的机器学习方法进行比较，评价指标为准确率(ACC)、查准率(P)、漏报率(FNR)，如表5所示。

通过对比目前常用的入侵检测算法可以看出，一些经典的机器学习算法，比如SVM和KNN算法实验效果较差，漏报率很高，而几种深度学习算法

图6 准确率和代价函数曲线Fig.6 Accuracy and cost function curve

图7 三种深度学习算法对比Fig.7 Comparison of three deep learning algorithms

表5 模型对比Table 5 Model comparison

在各个指标上明显好于经典的机器学习方法，其中DSCNN-BiLSTM算法具有更高的准确率、更低的漏报率。最后针对5种不同数据类型，将本文方法与上述方法进行分类准确率的对比，如图8所示。

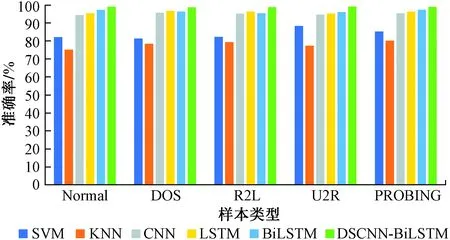
图8 不同方法对5种数据类型的准确率对比Fig.8 Comparison of accuracy of five data types by different methods

由图8所示，DSCNN-BiLSTM算法对于5种数据类型的准确率分别为99.2%、98.8%、98.9%、99.3%和99.1%，均高于其他算法，证明了该方法的性能最佳，大大提高了入侵检测的准确率。

4 结论

在互联网时代快速发展的今天，网络流量数据的数量、复杂度和特征维度都在不断增大，传统的统计学方法、机器学习方法已经不能满足当前入侵检测的需求。提出了一种基于DSCNN-BiLSTM的入侵检测方法，该方法将基于主成分分析的特征选择和融合的深度学习方法相结合，使用深度可分离卷积神经网络(DSCNN)提取网络流量数据的空间特征，引入了深度可分离卷积代替传统的卷积，使得模型轻量化；应用双向长短期记忆网络(BiLSTM)顺序敏感性的优势，充分考虑前后特征之间的影响，挖掘网络流量数据的时间特征。实验结果表明，与其他方法相比，显著提高了入侵检测的准确率，降低了误报率。但是由于入侵检测测试所用的是KDDCUP99数据集，缺少对当前实际网络环境中网络流量数据的验证测试，因此，下一步计划将该入侵检测模型部署在网络防火墙上，实时抓取网络流量数据，检测该模型的实时性能。