基于EtherCAT和TwinCAT3的协作机器人控制系统设计

2021-04-22袁俊杰刘海涛潘国庆王红伟

科学技术与工程 2021年8期

袁俊杰, 刘海涛, 潘国庆，王红伟

(1.北方工业大学机械与材料工程学院，北京 100043； 2.北京航天测控技术有限公司研发中心，北京 100041)

中国确定通过“三步走”实现制造强国的战略目标，第一步是到2025年迈入制造强国的行列。但是目前中国作为制造大国，仍有很多劳动密集型产业，这些产业迫切需要产业升级，而机器人作为产业升级的重要推动力量，受到越来越多的关注。传统工业机器人节约了成本，提高生产效率，但也存在缺点，工业机器人缺乏与人之间的协作、交互[1]。而协作机器人体积小巧，可以协助人完成一些任务，比工业机器人更便捷、更智能。机器人的核心是控制系统，控制系统包括硬件和软件两部分。

国际上，机器人公司所配备的控制系统大多是封闭式结构[2]，“四大家族”的机器人都有自己的控制系统，不适合二次开发维护。所以开放式的控制系统对于二次开发十分重要[3-4]，开放式机器人运动控制系统的硬件系统主要分为基于VME(versa module eurocard)总线的机器人控制系统和基于PC(programmable controller)总线的机器人控制系统两大类[5]。按控制系统架构，一般可以分为基于PLC(programmable logic controller)的控制系统、基于嵌入式的控制系统[6]、软件型控制系统[7]、基于PC总线的控制系统[8]。

在中国，协作机器人的控制系统有一些基于机器操作系统(ROS)[9]，但存在开发难度大等问题。有学者尝试使用EtherCAT(Ethernet for control automation technology)总线开发机器人，如王力宇等[10]提出了一种基于x86平台和EtherCAT总线的运动控制器设计，史步海等[11]提出一种基于实时Linux平台下的采用EtherCAT总线的六轴关节型机械手实现方案。

通过以上分析，传统的控制系统不开源，开发难度大，因此提出一种基于EtherCAT和TwinCAT3(the windows control and automation technology)的协作机器人控制系统的设计方法，可缩短机器人控制系统的研发周期。采用嵌入式工控机作为硬件平台，利用TwinCAT3作为上位机，高速EtherCAT现场总线作为媒介，实现对协作机器人的控制。在TwinCAT Measurement基础上，实现机器人直线和圆弧的轨迹规划和碰撞检测分析等功能。

1 协作机器人运动学分析

1.1 正运动学求解

参考深圳市泰科公司的TA6-R5型协作机器人，对机器人的结构参数进行建模，TA6-R5协作机器人由基座(1轴)、肩关节(2轴)、肘关节(3轴)、腕部(4、5、6轴)组成。在此基础上各个关节安装力矩传感器，TA6-R5协作机器人的UG模型如图1所示。

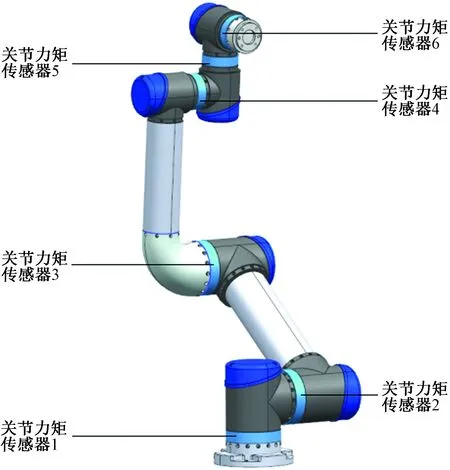
图1 TA6-R5协作机器人Fig.1 TA6-R5 collaborative robot

为了描述机器人末端在空间的位姿，需要在机器人的各个关节上建立坐标系，利用坐标系与坐标系之间的关系表示位姿，采用Denavit-Hartenberg(D-H)法[12]建立运动学模型，各关节坐标分布如图2所示。

6-DOF(degree of freedom)的TA6-R5协作机器人D-H参数如表1所示。

图2 六自由度机械臂坐标系分布Fig.2 Coordinate system distribution of 6-DOFs manipulator

表1 协作机器人的连杆参数

(1)

式(1)中：

(2)

式(2)中：余弦cosθi=cθi=ci；正弦sinθi=sθi=si；c23=c2c3-s2s3；s23=s2c3+c2s3；c234=c23c4-s23s4；s234=s23c4+c23s4。

1.2 逆运动学

(3)

整理式(3)，将含有θ1和θ6的部分移到方程的左边，得到

(4)

通过式(4)，可以求解出θ1和θ5，即

(5)

式(5)中：

(6)

整理式(1)，将含有θ1的部分移到方程的左边，得

(7)

当s5≠0的时候，可以解出θ6，即

(8)

当s5=0时，该机械臂处于奇异位形,这种状态将不在本文中具体讨论。

通过式(7)，还可以得到

(9)

式(9)中：

(10)

利用式(9)可以得到θ4和θ3,即

(11)

通过上述计算，可以得到求出各个关节角的解析解，即

(12)

串联机械臂一般都存在多解问题，实际应用时要考虑机械臂实际的运动空间范围，是否需要避障、轨迹最优、能耗消耗最少等原则选择一组最优的逆解。

1.3 MATLAB运动学验证

为了将机器人应用于实际工作中，利用MATLAB结合Robotics Toolbox验证正逆运动学的正确性。正运动学验证如图3所示，给定任意一组关节角，分别代入运动学函数和Robotics Toolbox中fkine函数，观察得到的末端执行器的位姿矩阵是否一样。如果得到同一个末端矩阵，将其代入逆解函数，如果8组逆解中有一组和输入的一致，并且将8组逆解全部代入fkine中，如果得到和原来相同的结果，证明正逆运动学正确。

图3 正运动学验证Fig.3 Verification of kinematics solutions

(0,-π/2,π/2,3π/4,3π/2,π/6)是任意给定的一组关节角，π代表圆周率，代入代入计算得到的运动学函数和Robotics Toolbox中fkine函数中，计算得到的结果为

(13)

在上述给定的关节角度下，MATLAB机器人工具箱中机械臂位姿如图4所示。

图4 MATLAB机器人工具箱中机械臂位姿Fig.4 Manipulator posture in MATLAB robotics toolbox

观察发现T1=T2，证明正运动学计算正确，再将其代入逆运动学函数中，协作机器人运动学8组逆解如表2所示。

观察表2，发现第四组逆解中除了θ5，其他角度与给定的关节角完全一致，MATLAB中四象限反正切atan2函数返回值在±π之间，所以θ5=3π/2-2π=-π/2≈-1.570 8，这时可与所给关节角全部对应起来。将表2中8组关节角代入正运动学公式，在误差允许的范围内，得到的结果是同一个末端位姿T1，由此验证所求的正逆运动学公式正确。

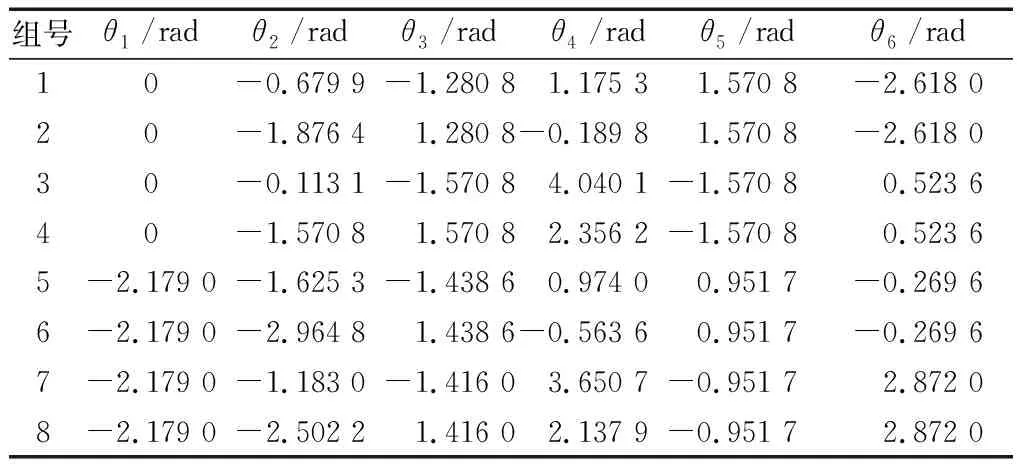
表2 8组逆解中的θ1～θ6Table 2 θ1～θ6 of eight inverse solutions

1.4 基于蒙特卡洛法的工作域分析

工作域是机器人操作中心点所能达到的所有位置的集合，采用蒙特卡洛法，用概率的方法计算机器人的工作域。根据正运动学可以得到机器人末端的位置(px,py,pz)，在MATLAB中，根据式(14)，会得到一组关节角组：

θ=θmin+(θmax-θmin)×rand

(14)

式(14)中：θ为各个关节角度；θmax为每个关节角能取得的最大值；θmin为每个关节角能取得的最小值；rand是产生均匀分布的随机数的函数。

在MATLAB中利用plot3函数画出所有所有关节角对应的空间点，循环的次数越多，随机数取的组数越多，结果越精确。本文中随机数取100 000，三维空间和二维空间的空间工作域如图5所示。

图5 三维空间和二维空间的机器人工作域Fig.5 The working field of the robot in three dimensional space

2 机器人控制系统设计

机器人一般以整机为单位，控制系统底层协议基本不对用户开放，而选用以关节模组为单位的协作机器人，可以从驱动器层面开发控制算法。控制系统的总体方案，如图6所示。

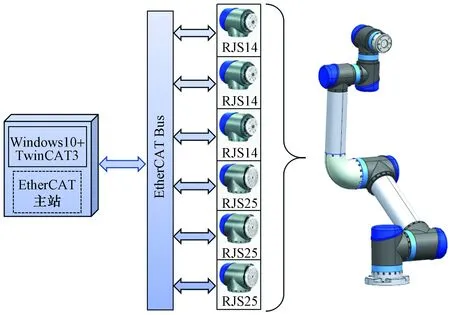
图6 控制系统总体方案Fig.6 Overall scheme of control system

2.1 硬件设计

控制系统以嵌入式工业控制计算机为控制平台，鉴于机械臂控制对实时性要求更高，同时考虑该机器人系统需求对于数据采集和传输的需求，采用EtherCAT现场以太网总线实现机器人各关节的协同控制。

控制系统所选用的RJS系列关节模组中集成的驱动器选择了具备完善的EtherCAT接口控制的RDM系列驱动器，支持CoE(CANopen on EtherCAT)，该一体化机器人关节模组使控制器结构大大简化的同时，能够利用高速EtherCAT网络保证整个系统的实时控制需求[13]。

2.2 基于TwinCAT3的软件设计

TwinCAT3是德国倍福推出的基于PC的控制软件，不仅支持IEC 61131-3编程标准，而且允许使用高级语言C++及MATLAB/Simulink。TwinCAT3配合EtherCAT现场总线，可连接外部IO设备，实现对机器人的控制。

2.2.1 程序POUs设计

TwinCAT3中的POUs(program organization units)程序是控制系统的主体，POUs主要包含MAIN函数和Function Block，如图7所示。TwinCAT3允许使用IEC61131-3编程标准中5种语言的任意一种编程语言，也可用多种语言联合编程。由于ST(structured test)语言移植性好，在不同的PLC上移植比较容易，所以选用ST语言作为该控制器的主要编程语言。

PLC程序中，和外部IO联系的变量需要进行变量链接，被链接的变量声明在GVLs(global variable lists)中，链接对象需在对象字典中进行添加。当在IO中进行变量链接时，以1轴状态字为例，在Drive 1的Transmit PDO 5中选择Status word，右击Change Link，然后在GVLs中定义的status_word，双击可完成变量链接，如图8所示。

图7 MAIN函数以及Function BlockFig.7 MAIN Function and Function Block

变量链接完成以后，在MAIN主程序区可以对所定义的变量进行读写操作，当自定义变量和外部IO变量链接以后，通过周期扫描刷新会更新关节模组中的各项数据，实现控制功能。

2.2.2 利用C++编写逆解等复杂函数

运动学逆解计算复杂且涉及四象限反正切atan2等函数，如果在POUs中利用ST语言计算逆解，会浪费CPU资源，使整个程序的运行变慢，所以在C++中完成逆运动学求解，将C++逆解发布成模块，PLC调用模块。

在TwinCAT Driver Project中选择TwinCAT Module Class创建C++，在tmc(TwinCAT module class editor)中配置输入参数以及返回值，如图9所示。

图8 GVLs变量链接过程Fig.8 The link process of GVLs variables

图9 C++模块tmc配置Fig.9 C++module tmc configuration

由逆解得出逆解矩阵double theta_Med[8][6]，每一行是一组逆解。Current_Theta1-Current_Theta6也是逆解函数的输入变量，作用是在8组逆解选取最优解，选取原则是根据各个关节每次运动所旋转的关节角度绝对值之和最小，选取最优解的具体程序如下：

double qiuhe[8] = { 0,0,0,0,0,0,0,0 };

for (i = 0; i < 8; i++)

{

if (theta_Med[i][1]>-PI && theta_Med[i][1]<0 && theta_Med[i][2]>-8 * PI/ 9 && theta_Med[i][2] < 8 * PI/ 9)

{qiuhe[i] = fabs_(theta_Med[i][0]-

Current_Theta1)+fabs_(theta_Med[i][1]-

Current_Theta2)+fabs_(theta_Med[i][2]-

Current_Theta3)+fabs_(theta_Med[i][3]-

Current_Theta4)+fabs_(theta_Med[i][4]-

Current_Theta5)+fabs_(theta_Med[i][5]-

Current_Theta6);

}

else

{qiuhe[i] = 100;}

}

double Min = qiuhe[0];

int Temp = 0;

for (i = 1; i < 8; i++)

{

if (Min > qiuhe[i])

{Min = qiuhe[i];Temp = i;}

}

return theta_Med[Temp][0];

返回值theta_Med[Temp][0]是筛选出的最优解，即第一轴的关节角，将作为Resolve_Theta1()函数的返回值；同理Resolve_Theta2～Resolve_Theta6会返回关节2到关节6的关节值。

C++函数编写完成以后，通过TwinCAT Publish Modules发布。发布成功以后在PLC中调用C++模块。调用时在POUs中建立用于逆解运算的Inverse_Kinematics功能块，并添加FB_exit、FB_init以及Resolve_Theta1～Resolve_Theta6等方法，Resolve_Theta1配置如图10所示。

2.2.3 人机交互界面设计

控制器的程序运行在系统内部，和操作人员交互的是HMI(human machine interface)，TwinCAT3提供了HMI设计控件，控件也需要进行变量链接。在HMI中主要有开抱闸、一键回原点、电流检测预警、各项数据实时显示以及直线和圆弧轨迹规划等功能，激活以后，如图11所示。

(15)

图10 Resolve_Theta1配置Fig.10 Resolve_Theta1 configuration

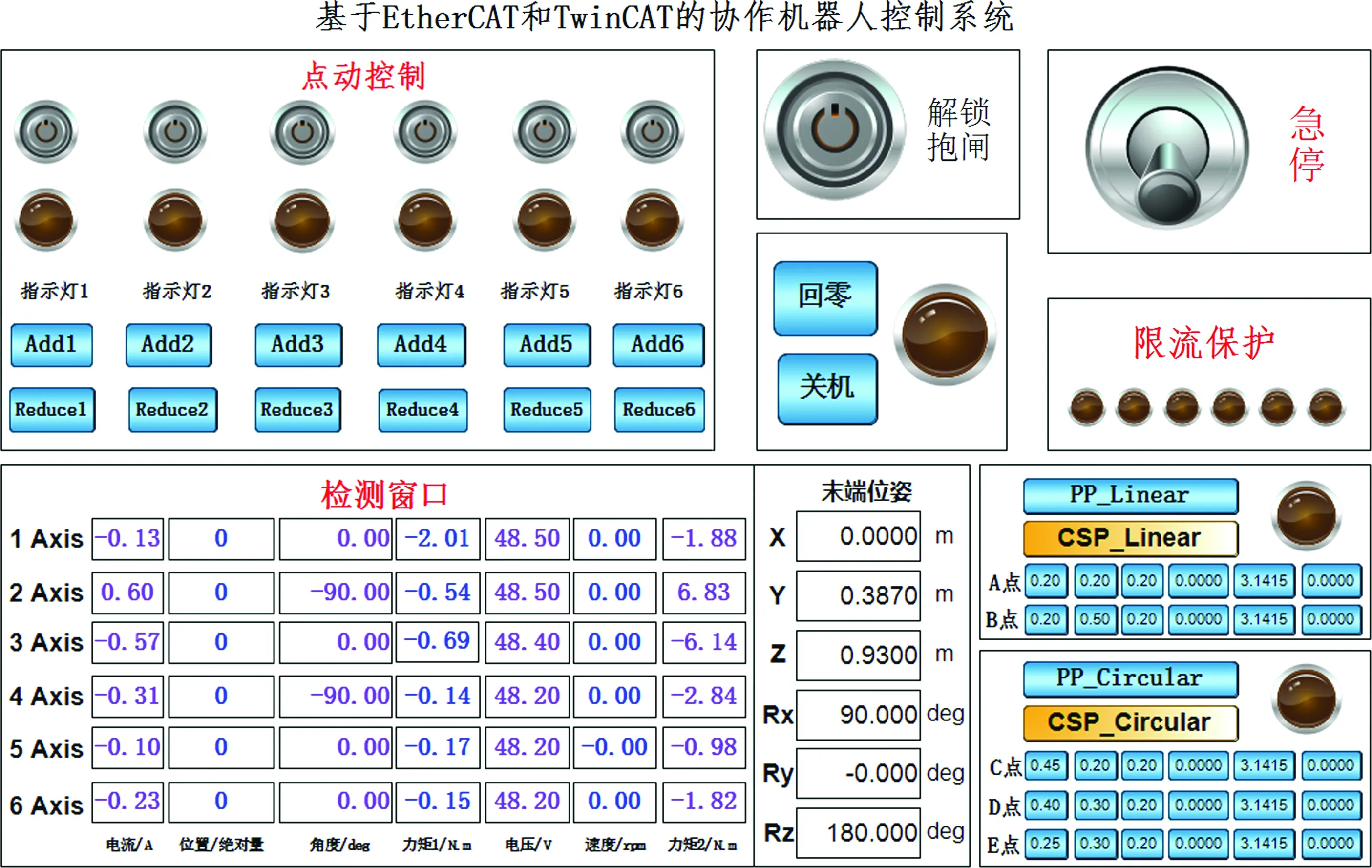
图11 HMI界面Fig.11 HMI interface

根据PLC程序运行机制，MAIN总是在周期刷新所有命令。如果有HMI的外部触发，则判断语句IF O_To_A_Step_Enable = TRUE THEN为真，程序会运行Linear_Interpolation_A_B_1.O_To_A()，进行原点O到A点的运动。A点到B点运动时，二维数组Theta_A_B_Med在每个Tasks周期内刷新，计算刷新后，Theta_A_B_Med中第一个元素是次数，第二个元素是每个关节角度信息，减去上次运动的角度，得到的相对值是本此扫描周期中的实际运行角度，将其赋值给0x607A，可以指导硬件完成运动。TwinCAT3中赋值角度运行信息程序如下所示：

target_postion[Var_1]:=LREAL_TO_DINT

(

(Theta_A_B_Med[Var_1+1,Var_2]-

Theta_A_B_Med[Var_1+1,Var_2-1]

)/(2*PI)*131 072

)。

通过上述步骤，可以实现空间直线等轨迹的运行。

3 TwinCAT3控制系统性能测试

为验证基于TwinCAT3搭建的控制系统控制的性能，以泰科智能伺服技术有限公司的TA6-R5协作机器人作为实验对象，在各个关节安装扭矩传感器，利用关节模组提供的模拟量接口采集数据，并网到EtherCAT总线中。采用PLC-ST语言在TwinCAT3的PLC中编写程序，逆解程序利用C++编写，并发布成模块以供PLC调用，这样可降低PLC程度的复杂程度，提高CPU的运行速度。最后利用TwinCAT3的图形化输出的分析工具Scope View，可以获取变量，对其记录并显示。

3.1 运动学验证和Scope View分析

根据同步周期位置模式，在笛卡尔空间中轨迹规划时需要将规划的轨迹适当细分，控制器周期发送关节角信息，驱动器会自动进行插补，运行速度取决于细分步数以及PLC程序周期扫描时间。设轨迹是从空间(0.2，0.2，0.2)沿着直线运动到(0.2，0.4，0.2)，角度为(0,π,0)。在Solution中添加YTScope Project，记录运动中的空间位置Px、Py、Pz。然后点击Start Record，轨迹图Chart如图12所示。

设以(0.325，0.2，0)为圆心，0.125 m为半径，位姿是(0,π,0)的圆轨迹。在Solution中添加XYScope Project记录圆轨迹时的笛卡尔二维空间XOY平面中的Px、Py。Chart如图13所示，A点是机器人机械位置原点，实际运动时机器人末端从原点运动到起始点B，然后以逆时针方向运动。

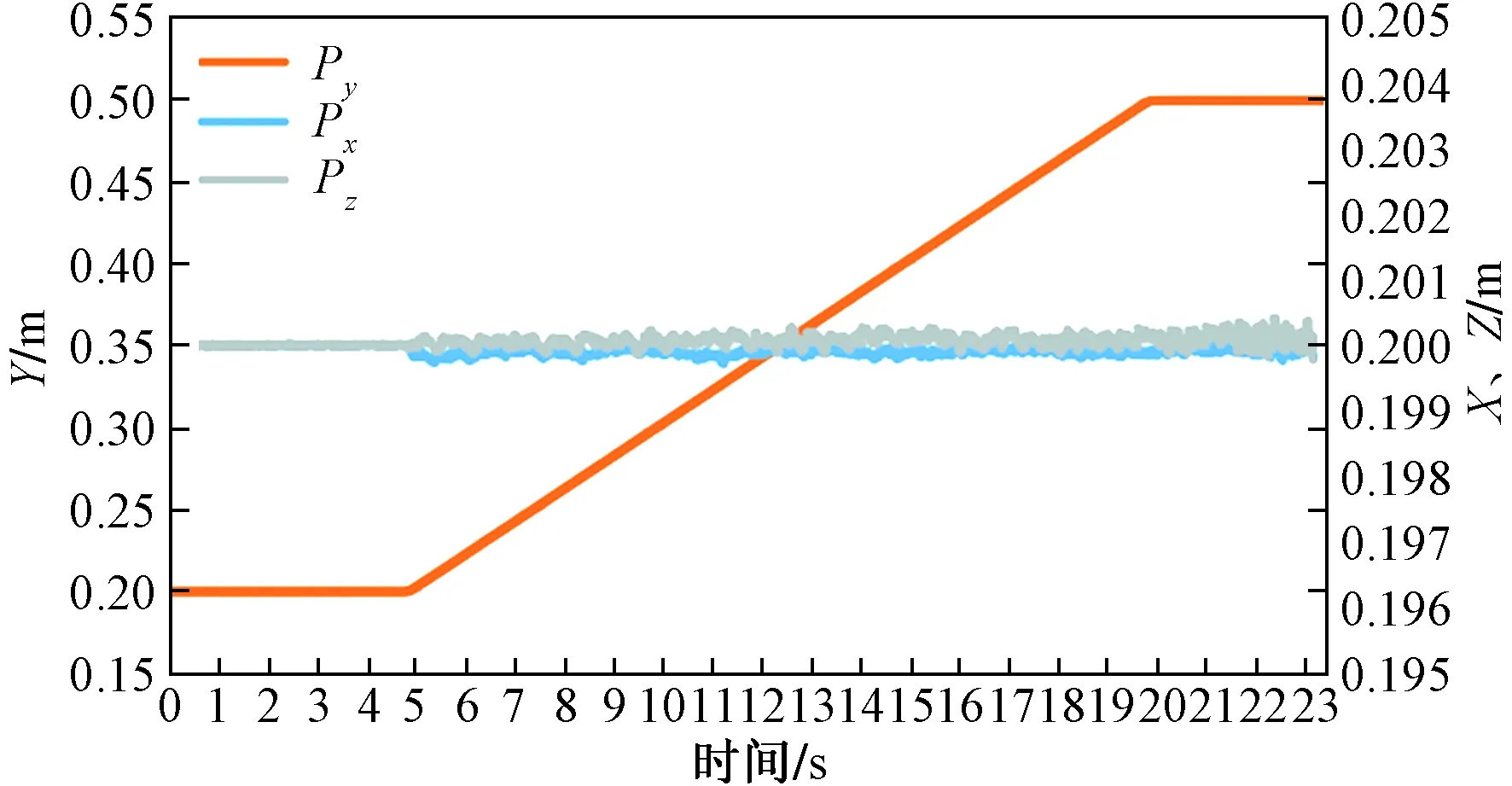
图12 YT Scope ProjectFig.12 YT Scope Project

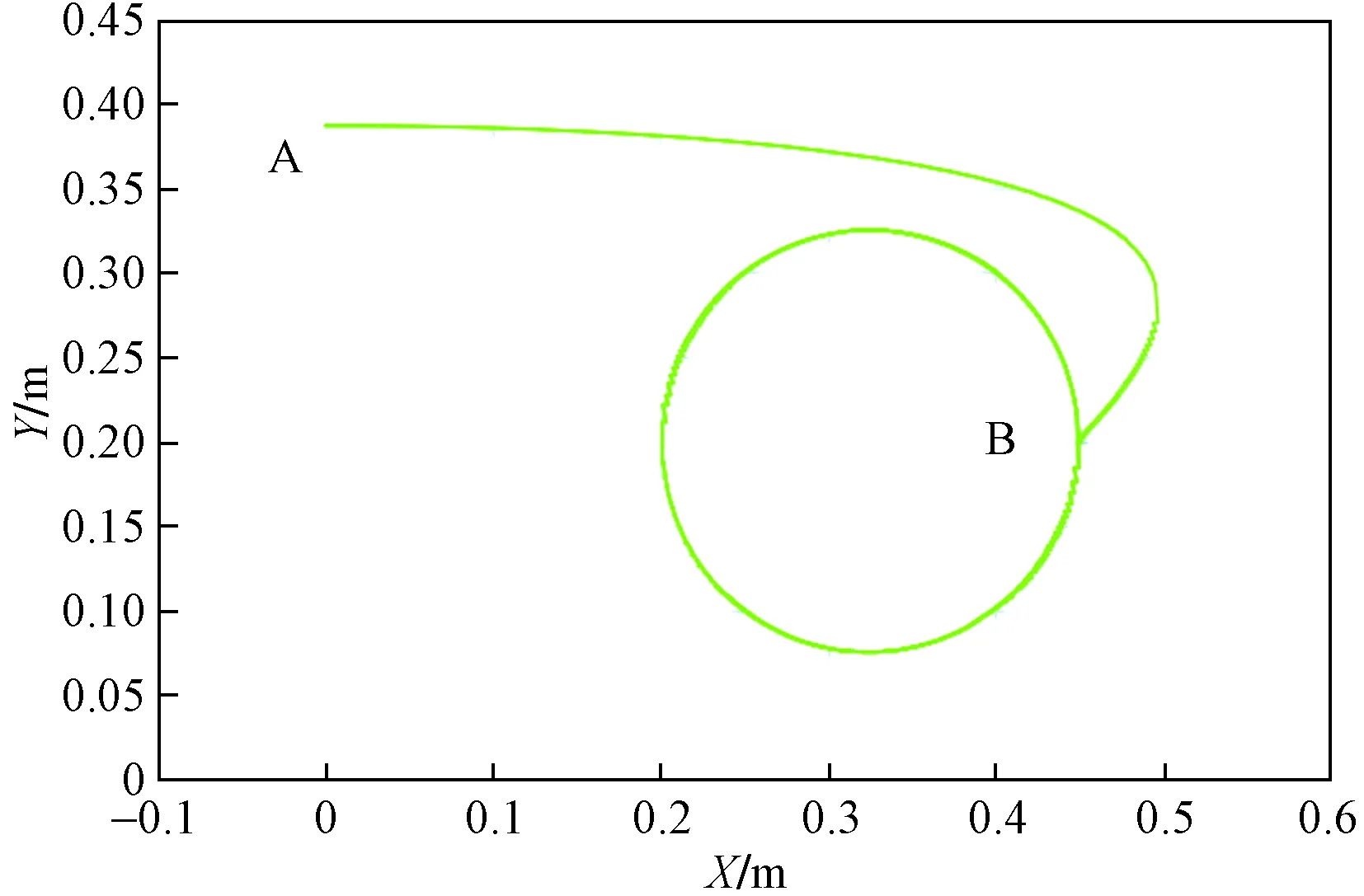
图13 XY Scope ProjectFig.13 XY Scope Project

实验平台上的机械臂将按照预先设定的运动方式进行运动，CSP模式下细分2 000，PLC扫描周期是5 ms，所以运动1圈的时间为10 s，每隔2 s取一次实物运行状态，如图14所示。

图14 协作机器人运动实验Fig.14 Motion experiment of cooperative robot

观察图14，机械臂按照逆时针方向的圆轨迹运动，和如图13所示的笛卡尔XOY平面上的轨迹吻合，所以实验上验证了运动学正确性，以TwinCAT3为平台的控制器可以实现期望轨迹运动。

3.2 碰撞检测实验

当协作机器人运动时，遇到障碍或者碰撞能立即停止运动，由于各个关节加装扭矩传感器，可以利用扭矩值的变化来实现碰撞检测。机器人按照如图13所示轨迹运动2圈，以2轴为例，当无碰撞时，关节力矩如图15所示。在3、8、17 s时，人为产生3次不同力的碰撞，关节力矩如图15所示。观察发现，发生碰撞时，关节力矩会发生明显的波动。

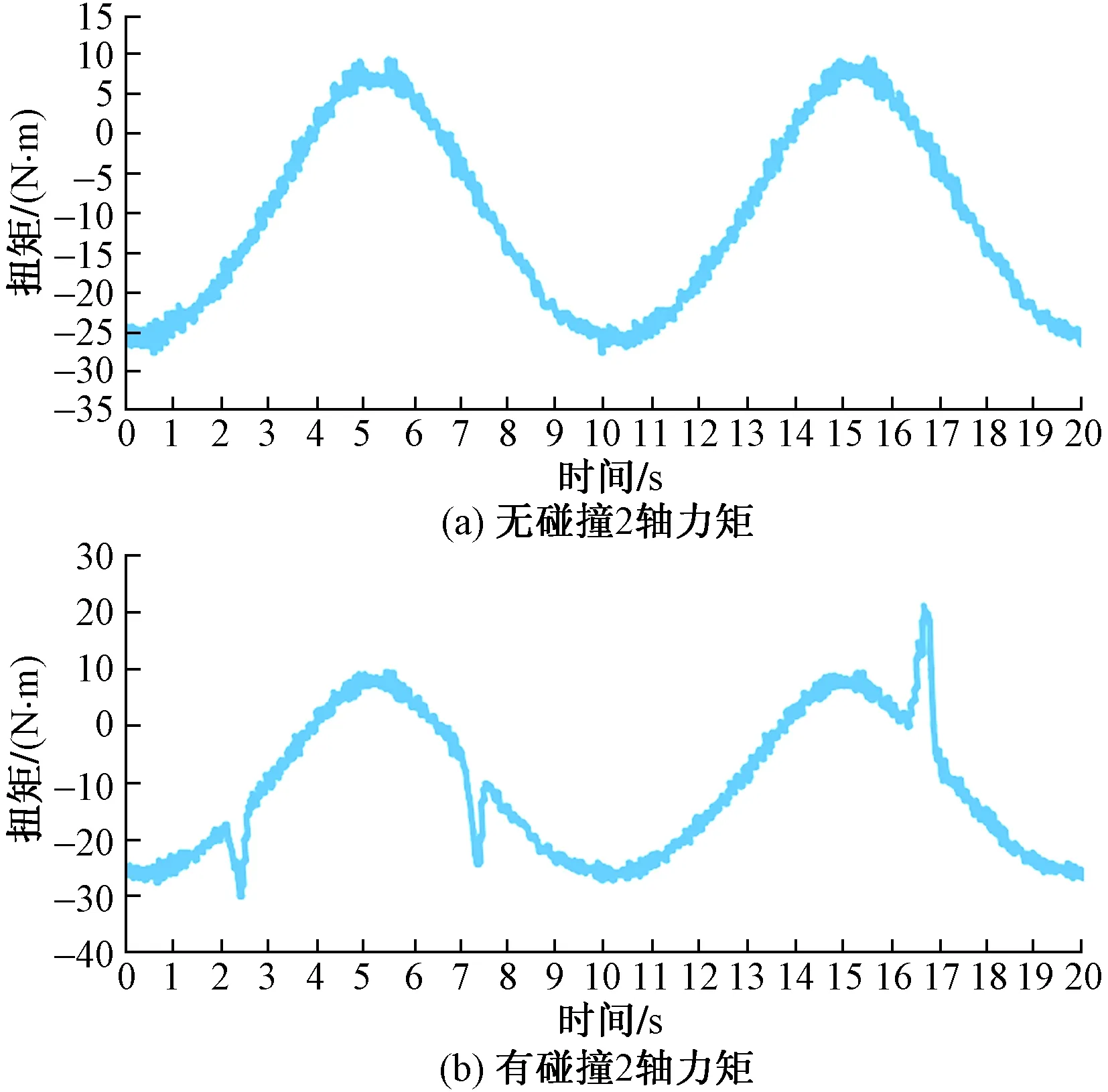
图15 机器人2轴力矩变化曲线Fig.15 Curve of second axis torque of the robot

通过运动学分析以及碰撞实验，控制系统是以EtherCAT总线为基础，需要验证程序执行的实时性，TwinCAT3中有检测程序执行时间的功能块，观察nLastExecTime可以获得每个PLC扫描周期下的程序运行时间，如图16所示。观察发现，当程序运行时，nLastExecTime最大时间不超过600 000 ns，即0.6 ms，所以设计的控制系统实时性符合要求。