利用应变模态差识别弯管内部损伤

张丹富， 马 骐， 卫小龙， 杜国锋

(长江大学城市建设学院， 荆州 434023)

长输管道作为油气运输的重要途径被广泛应用于工程中，对国民经济也起至关重要的作用。在实际工程中为了防止管道因热胀冷缩、管道支撑或端点附加位移造成应力问题，常在管道设计中添加一定长度的弯管。以此避免造成过大的附加位移或应力。然而弯管受力较为复杂，且常服役于极端恶劣环境下受到众多不利因素的影响。长此以往极易导致弯管损坏甚至出现重大事故。为了减少管道事故的发生，加强对服役弯管及管道系统进行有效的损伤检测和评估，了解其健康状况是很有必要的。

在现有的结构无损检测技术中，基于振动模态的损伤检测方法因其具有简单易实现、方便检测的特点，被广泛应用于结构损伤检测领域[1-2]。该方法的原理是结构模态参数与物理特性之间存在函数关系，结构损伤导致物理特性改变，从而导致结构模态参数变化[3]。基于该原理，邓焱等[4]利用桥梁结构应变状况与刚度的直接关系来识别桥梁损伤。闫天红等[5]建立结构模态参数对以单元刚度为特征的结构损伤识别关系式，来识别结构损伤位置和程度。随着模态分析技术的日益成熟，以模态参数变化作为损伤指标来实现结构损伤识别已经成为常用的管道损伤检测方法之一[6-7]。因此众多学者对此展开研究，早期，Cawley等[8]基于结构因损伤导致固有频率改变的原理并结合有限元模拟来判断结构是否损伤。Salawu等[9]和高芳清等[10]利用固有频率变化的方法来识别结构损伤位置与程度。结果表明利用固有频率化无法识别对称结构损伤，另外该方法对微小损伤不敏感。因此利用位移模态或位移模态而衍生的其他参数进行损伤识别的方法被广泛应用起来[11-12]。利用固有频率变化识别损伤的方法无法有效的识别微小损伤，位移模态的一阶导为应变模态，所以直接利用应变模态的变化来判断结构损伤更为精确。韩红飞等[13]和许成祥等[14]分别以应变模态差和应变模态敏感比差作为损伤指标，直观准确地实现了直管的损伤识别。目前，对于直管的损伤检测研究成果较多，而利用应变模态变化识别弯管损伤的研究相对较少。为了获得精确有效的弯管内部损伤识别方法，现提出以模态应变差作为损伤指标来实现弯管内部损伤识别和定位。

基于位移模态和应变模态的模态叠加特性和正交性推导了应变模态差公式，利用有限元对不同内部损伤工况的管道模型进行分析。验证以模态应变差作为损伤指标识别弯管单损伤、双损伤以及多损伤位置和损伤程度的可行性。并通过建立不同径厚比和不同弯曲形式的弯管模型，验证损伤指标对弯管内部损伤识别具有可行性和普遍性。

1 弯管应变模态差有限元数学模型

利用模态坐标建立方程时，将模态振型作为系统基向量来描述结构振动状态。当结构做无阻尼振动时，基于结构动力学知识可知，结构的模态振型是其变形的固有动态平衡状态。由模态正交性可知，各固有的平衡状态是相对独立的，不依赖于其他平衡状态而存在。每种固有平衡状态都能够满足节点之间的平衡性和相容性。虽然各固有模态之间互不耦合，但由各模态振型按一定比例叠加可以得到结构响应。位移模态的振型向量相对于质量矩阵、刚度矩阵和阻尼矩阵满足正交性。基于这个概念，位移响应表示为

(1)

式(1)中：φr为第r阶位移模态；qr为φr的模态坐标。

在有限元模型中令ε为结构P个单元的总体节点应变向量，δ为P个单元的总体节点位移向量，B为P个单元几何矩阵。考虑到总体坐标系和局部坐标系之间的转换关系,令坐标转换矩阵为β，B′=Bβ。则总体坐标中节点位移向量δs=B′-1ε。 根据考虑结构阻尼情况下的多自由度系统振动微分方程可得

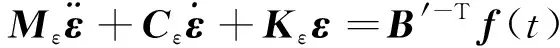
(2)

式(2)中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；f为外荷载向量。

根据模态叠加法原理得

(3)

将式(3)代入式(2)后得

ΨεTB′f(t)

(4)

(5)

由于Mr、Cr与Kr均为对角矩阵，因此式(5)表明应变模态振型之间的加权正交性。Ψε=B′φ可以表示为ΨεTB′-T=φT，将式(5)代入式(4)可得

(6)

式(6)与位移坐标系下表达形式相同，说明应变模态的各阶模态坐标与位移模态中对应的模态坐标相同，即q′=q。应变模态与位移模态是系统统一能量平衡状态的两种表达形式，因此应变模态也能够满足正交性和模态叠加特性。则应变响应可表示为

(7)

根据多自由度模态分析理论，结构位移响应公式为

(8)

式(8)中：xN表示第N阶位移响应；ω表示固有频率；mr表示模态质量；kr表示模态刚度；cr表示模态阻尼；F表示力响应。

(9)

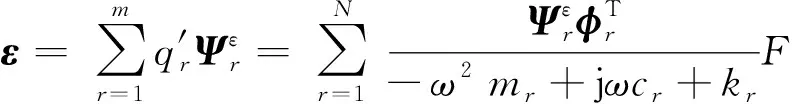
(10)

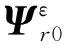
(11)

2 弯管损伤识别数值模拟

2.1 有限元模型建立

为了验证以应变模态差作为损伤指标识别弯管内部损伤的可行性，采用一端铰接一端简支的U形弯管作为研究对象，如图1所示。利用大型商业软件ABQUS建立弯管有限元模型，该模型长度为1.8 m；管道的内径和外径分别为d=62 mm和D=70 mm；管道材料的弹性模量E=206 GPa;泊松比取μ=0.3；材料密度取ρ=7 850 kg/m3；采用 C3D8R 实体单元建立的该管道有限元模型，根据管道尺寸参数，沿管道轴向方向划分为12个单元，13个节点，沿管壁厚度方向均匀划分为4个单元，周向划分为24个单元。

图1 弯管模型示意图Fig.1 Schematic diagram of the elbow pipe model

通过局部网格剔除来模拟管道模型内部损伤，损伤的轴向宽度用B来表示，径向深度用H表示，周向长度用L表示。模拟9种不同的损伤工况讨论弯管单损伤和多损伤的识别情况，以双损伤和三损伤为例来研究弯管多损伤工况下的损伤识别方法；并通过改变内部损伤的轴向宽度来研究其对弯管损伤识别的影响。为了减小误差内部损伤均设置在每个单元轴向长度的中间位置。工况如表1所示，模拟计算得到的不同工况下弯管前5阶频率如表2所示。

表1 管道模型模拟工况

2.2 单损伤识别

设定单损伤的位置分别在试件G1第2单元和G2第6单元，损伤尺寸设置为：B×H×L=2×2×66π。模拟所得管道第5阶应变云图如图2所示，据模拟结果绘制管道单元节点的前5阶应变模态差曲线图，如图3所示。根据图3(a)可知试件G1的应变模态差值在单元节点2和3处出现明显的突变趋势，而其他单元节点的应变变化趋势相对平缓。因此很容易判断损伤单元为弯管的第2单元。由图3(b)可知，试件G2的应变模态差模态差值的值在单元节点6和7处出现明显的突变，而其他单元节点变化趋势较为平缓。由此可判断试件的损伤单元在弯管的第6单元。改变第6单元内部损伤的轴向宽度，建立内部损伤轴向宽度B分别2、4、6 mm的弯管G2、G3、G4模型进行分析。根据计算结果，为了方便，清晰地得到内部损伤轴向宽度变化对应变模态差的影响。取单元节点第3阶和第5阶应变模态差绘制曲线图，如图3(c)所示，结果表明，即使改变单元内部损伤的轴向宽度，以应变模态差作为损伤指标仍然可以识别弯管单个损伤的存在与损伤位置。图3(d)为管道损伤单元节点应变模态差随损伤轴向宽度变化图。可以看出，随着内部损伤轴向宽度的增加，反映损伤的节点突变峰值也会随之增大。所以，利用应变模态差作为损伤指标不仅可以有效地对弯管进行单损伤定位，也能反映弯管的损伤程度。

表2 不同损伤工况下的前5阶频率

图2 不同单损伤工况下应变云图Fig.2 Strain nephogram under different single damage conditions

图3 单损伤弯管应变模态差Fig.3 Strain modal difference of single damage elbow pipe

2.3 多损伤识别

2.3.1 双损伤识别

为了研究U形弯管双损伤识别的方法，设定G5在第2单元和第6单元具有相同几何尺寸的内部损伤。损伤尺寸设置为B×H×L=2×2×66π。模拟所得双损伤管道第5阶应变云图如图4所示，根据模拟结果绘制带双损伤管道G5的前5阶应变模态差曲线图，如图5(a)所示。由前5阶应变模态差曲线可知，单元节点2、3和单元节点6、7处的应变模态差值都发生明显的突变，从而可以判断出G5的损伤单元为不相邻的第2单元和第6单元。为了研究基于应变模态差识别相邻双损伤的可行性，设定弯管G6在第5单元和第6单元具有相同几何尺寸的内部损伤，损伤尺寸与G5相同。模拟分析所得前5阶应变模态差值曲线如图5(b)所示。可知，单元节点5、6、7处的应变模态差值都发生明显突变，由于两带损伤单元相邻导致节点6反映损伤的峰值最大。从而可以判断损伤单元为相邻的第5单元和第6单元。综上所述，说明了利用应变模态差作为损伤指标可以实现弯管相邻与不相邻的双损伤识别，与单损伤U形弯管相同，2个单元的损伤程度增大，反映损伤的应变模态差突变峰值也随之增大。

图4 不同形式双损伤工况下应变分析云图Fig.4 Strain analysis nephogram under different double damage conditions

图5 双损伤弯管前5阶应变模态差Fig.5 The first five frequencies strain modal difference of double damage elbow pipe

2.3.2 三损伤识别

对于U形弯管多损伤识别，建立在第2、6、9单元和第4、7、10单元均带有相同程度内部损伤的管道G7和G8模型，损伤尺寸设置为B×H×L=2×2×66π。 模拟所得三损伤管道第5阶应变云图如图6所示，根据模拟结果得三损伤管道的应变模态差曲线如图7所示。从图7(a)中可看出，单元节点2、3节点6、7以及节点9、10处的应变模态差发生明显的突变。根据突变节点可判断第2、6、9单元为弯管的3个损伤单元。同理，根据图7(b)突变节点可以判断出第4、7、10单元为弯管的3个损伤单元。改变损伤单元的位置和损伤程度依旧能实现多损伤识别，改变单元损伤程度也会得到与单损伤和双损伤识别一样的规律，损伤单元节点的应变模态差会随损伤程度的增大而增大。

图6 不同形式三损伤工况下应变云图Fig.6 Strain analysis nephogram under different three damage conditions

图7 三损伤弯管前5阶应变模态差Fig.7 The first five frequencies strain modal difference of three damage elbow pipe

3 管道径厚比与不同弯曲形式对损伤识别的影响

3.1 径厚比

为了研究U形弯管径厚比改变对损伤识别的影响，建立不同径厚比损伤前、后的管道模型来对其展开研究。管道长度不变，损伤单元均为第6单元，损伤尺寸设置为B×H×L=2×2×66π。弯管3种径厚比分别设置为17.5、18.5、19.5，模拟所得不同径厚比弯管第5阶应变云图如图8所示。根据模拟计算结果，为了清晰地看出弯管径厚比改变对应变模态差的影响，取不同径厚比弯管的第3阶和第5阶绘制应变模态差曲线，如图9(a)所示。由图可知，改变管道径厚比，利用应变模态差作为损伤指标，仍然能实现对弯管内部损伤的存在与损伤位置的识别。根据图9(a)提取损伤单元的节点6、7的第3阶和第5阶应变模态差值进行分析，如图9(b)所示。由图可知，弯管应变模态差随径厚比的变化是无规律的。这是由于弯管径厚比变化改变了管道的固有特性，从而影响应变模态差的变化。

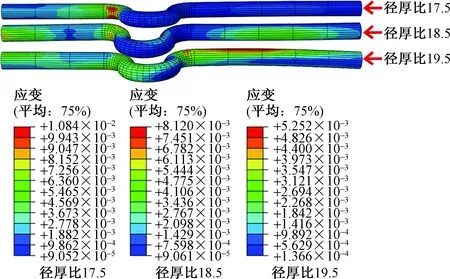
图8 不同径厚比损伤管道应变云图Fig.8 Strain nephogram of damaged pipes with different diameter-thickness ratio

图9 不同径厚比对弯管应变模态差的影响Fig.9 Effects of different diameter-thickness ratios on strain modal difference

3.2 不同弯曲形式

为了研究以应变模态差作为损伤指标识别弯管内部损伤的方法对不同弯曲形式管道的适用性，证明基于应变模态差识别弯管内部损伤具有普遍性。建立Z形、U形、S形3种不同弯曲形式损伤前、后的弯管对其展开研究。损伤尺寸设置为B×H×L=2×2×66π，缺陷位置均设置在第6单元。上述部分已经说明了损伤指标对U形弯管损伤识别的可行性，模拟所得的Z形和S形弯管第5阶应变云图如图10所示。根据模拟计算结果绘制前5阶应变模态差曲线，如图11所示。可知，Z形和S形弯管的应变模态差值均在单元节点6和单元节点7处出现明显的突变，而其他单元节点变化趋势较为平缓。由此可判断2种不同弯曲形式弯管的损伤单元为第6单元。改变损伤单元位置、增加损伤单元个数仍然能够识别损伤的存在和损伤位置，改变损伤单元的损伤程度，损伤单元节点的应变模态差值也随之增大。由此可知，以应变模态差作为损伤指标识别损伤的方法适用于不同弯曲形式的管道，基于应变模态差识别弯管内部损伤具有普遍性。

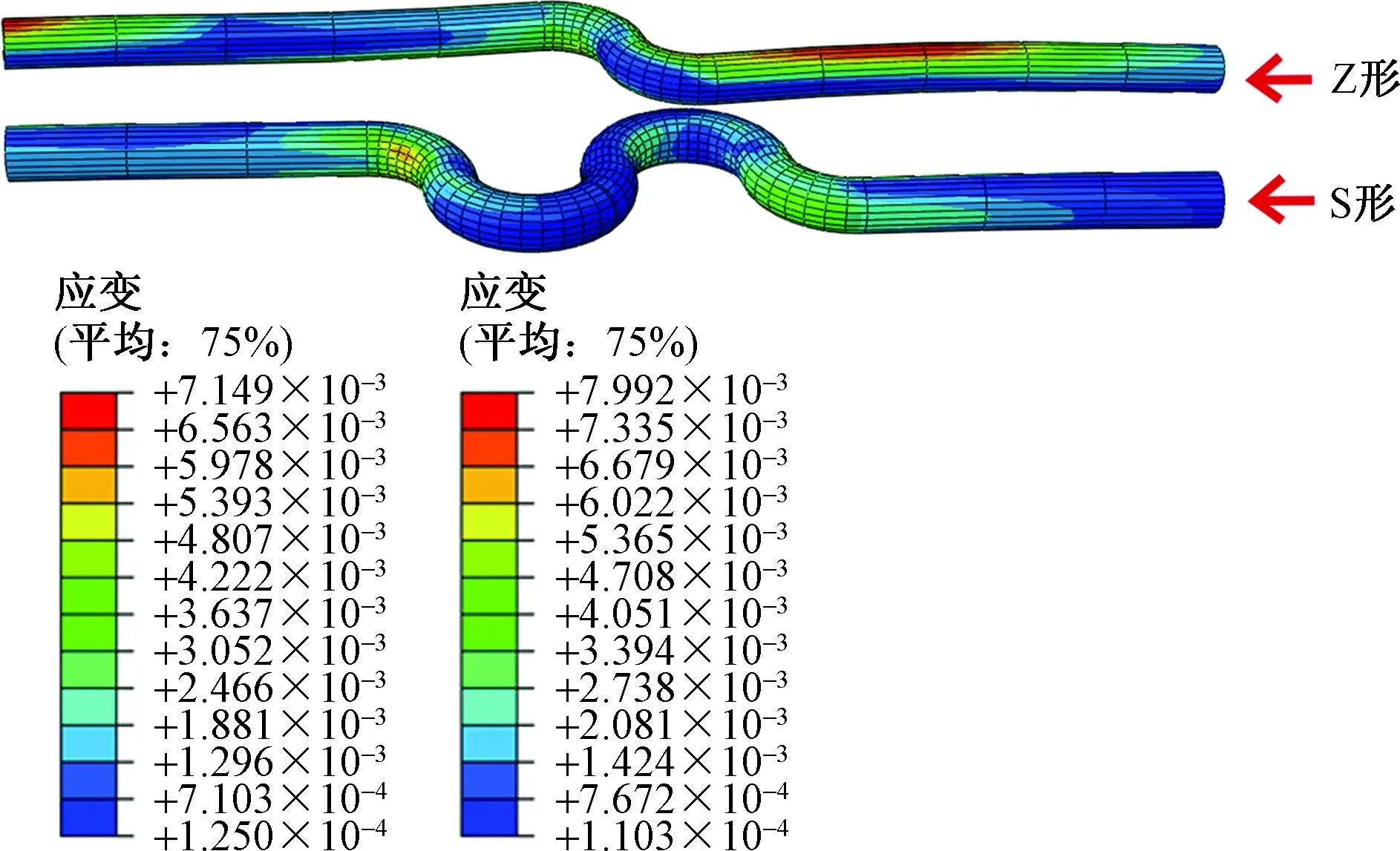
图10 Z形与S形损伤管道应变云图Fig.10 Strain nephogram of Z-shaped and S-shaped damaged pipes

图11 不同弯曲形式弯管应变模态差Fig.11 Strain modal difference of elbow pipes with different bending forms

4 结论

(1)以应变模态差作为损伤指标检测U形弯管内部损伤，可以识别U形弯管单个和多个损伤的存在以及损伤的位置。

(2)U形弯管损伤的单元节点应变模态差值随着内部损伤程度的增加而增大，通过损伤指标可以识别U形弯管内部损伤程度。

(3)改变U形弯管的径厚比或弯管的弯曲形式，仍然能通过应变模态差识别管道的内部损伤存在、损伤位置和损伤程度，证明基于应变模态差识别弯管内部损伤的方法具有可行性和普遍性。

(4)该方法仅利用前5阶低阶应变模态差便可实现弯管内部损伤识别，突出其简单和实用的优势。

(5)以应变模态差作为损伤指标可以识别弯管内部微小损伤的存在和损伤所在的位置。可利用该方法来检测服役弯管内部初始损伤，提高管道运行安全性。