Modelling of electronegative collisional warm plasma for plasma-surface interaction process

Plasma Science and Technology Laboratory,Department of Physics,Indian Institute of Technology Delhi,New Delhi-110 016,India

Abstract An electronegative collisional plasma having warm and massive positive ions,non-extensive distributed electrons and Boltzmann distributed negative ions is modelled for the plasma-surface interaction process that is used for the surface nitriding.Specifically the sheath formation is evaluated through the Bohm’s criterion,which is found to be modified,and the variation of the sheath thickness and profiles of the density of plasma species and the net space charge density in the sheath region in addition to the electric potential.The effect of ion temperature,nonextensivity and collisional parameter is examined in greater detail considering the collisional cross-section to obey power-law dependency on the positive ion velocity.The positive ions are found to enter in the sheath region at lower velocities in the collisional plasma compared to the case of collision-less plasma; this velocity sees minuscule reduction with increasing nonextensivity.The increasing ion temperature and collisional parameter lead to the formation of sheath with smaller thickness.

Keywords:electronegative sheath,ion temperature,non-extensivity,sheath thickness,power-law dependency,collisions

1.Introduction

Nowadays,plasma-based surface treatments[1,2]are widely adopted to enhance the mechanical and tribological properties of the materials which are widely used in the automobiles,semiconductors and microelectronics industries[3-7].When a conducting material comes in the contact with plasma,then there is a formation of a thin layer of the charged species at the interface of the plasma and material’s surface.Such a thin layer is termed as sheath that plays a momentous role in analyzing the plasma-surface interactions[8].The investigation of sheath characteristics in different plasma systems has been carried out by several researchers[9-28].The sheath characteristics have been found to show a distinct nature,when negative ions are introduced in the system[23,29-32].Many researchers have observed noteworthy influence on the characteristics of the probe in the cases of low-frequency sheath processes[33-35].X-ray emission has also been observed,when the laser light is launched on tin slab forming a sheath of ions that radiate[36-38].Langmuir probe analysis permits to measure the behaviour of plasma parameters in distinctive plasma systems[39].

The impact of ion temperature on the sheath characteristics in electropositive plasma has been studied by Crespo[16].The analysis of sheath formation in the presence of negative ions and warm positive ions has been carried out by Dhawan and Malik[9,29].Hatami[40]and Moulick et al[17]have investigated the presence of two varieties of positive ions in the electropositive and electronegative plasma,respectively,under the collisional environment.The impact of ionization rate on the sheath transition from electropositive to electronegative plasma has been examined by Crespo et al[18].Yasserian et al[26]have investigated the influence of the magnetic field in electronegative discharge.

It has been validated both experimentally and theoretically that for the low-pressure electronegative plasmas,the behaviour of the negative ion density is appropriated to illustrate with the Boltzmann distribution[41,42].A lowpressure electronegative plasma(Ar-O2)has been experimentally investigated by Ghim and Hershkowitz[41]through Langmuir probe analysis.They observed that the distribution of the negative ions follows Boltzmann relation with a temperature of 0.06±0.02 eV,while the resulting parameters werene=3.8 ×109cm−3andTe=0.69 eV.Here,positive and negative ions ofAr+and O−were formed.Franklin and Snell[42]have also shown for low-pressure electronegative plasmas that the spatial distribution of the negative ions is in well agreement with the Boltzmann distribution.

In space plasmas,the existence of high energy tail velocity distribution of the particles has been validated by distinct satellite measurements.Such particle distributions,which are deviated from the Boltzmann distribution,have also been implemented successfully on the stellar plasmas and solar winds[43,44].Moreover,the deviation in the distribution of the electrons from their well-known Boltzmann distribution has even been seen in the various laboratories measurements also.In 1994,Liu et al[45]have provided a strong confirmation of the presence of non-Maxwellian velocity distributions of electrons in a particular plasma experiment,where low-pressure argon gas(neutral densitynargon～1013cm−3and P～0.3 mTorr)was exposed to pulsed discharges.Langmuir probe data,i.e.probe currentIprobeas a function of probe voltageVprobeagreed with a non-Maxwellian distribution.Plasma density(electron density)ne=4 ×1010cm−3and electron temperatureTe=0.69 eV were the resulting parameters.Tsallis[46],therefore,has introduced new statistics which is labelled as non-extensive statistics or Tsallis statistics to investigate such systems where the distribution of the particles is far away from their Boltzmann distribution.Then in 1997,Tsallis and Souza[47]have demonstrated that the same experimental data can be well fitted with non-extensive thermo-statistical formalism.The impact of non-extensive distributed electrons and thermal positive ions has been investigated by Hatami[48]on electropositive sheath structure.Borgohain and Saharia[13]have introduced the q non-extensive electrons in electronegative plasma with cold positive ions.Safa et al[15]have studied the velocity distribution of non-extensive electrons in magnetised electropositive plasma sheath.The inspection of Debye length and floating potential in electropositive plasmas with non-extensive distributed electrons has been carried out by Sharifian et al[49].The examination of two non-Maxwellian electrons in unmagnetized electropositive plasma has been carried by Hatami and Tribeche[12].Basnet and Khanal[11]have analyzed the Maxwellian and non-Maxwellian electrons in magnetized electropositive plasma.The impact of ionization on sheath characteristics with two-temperature non-extensive distributed electrons has been investigated by Dhawan et al[21].

Researchers,while examining the impact of non-extensive distributed electrons on the sheath structure,have either neglected the temperature of positive ions or collisions or both,though the plasmas used for processing or plasma-surface interaction carry finite temperature ions and the ions may also have collisions with the neutral particles in addition to the usual collisions of electrons with the neutrals.Moreover,negative ions are intensely introduced for achieving better processing.Therefore,in the present work,we have modelled a collisional plasma which has negative ions and positive ions along with the electrons.This is done for understanding the plasma-surface interaction process via the generation of sheath on a metallic probe.For developing this model,positive ions,negative ions and electrons are respectively described by fluid approach,Boltzmann distribution and nonextensive distribution.

2.Basic equations for modelling

The basic equations required to investigate the collisional electronegative plasma with warm positive ions as fluid,qnon-extensive distributed electrons and Boltzmann distributed negative ions are stated as follows

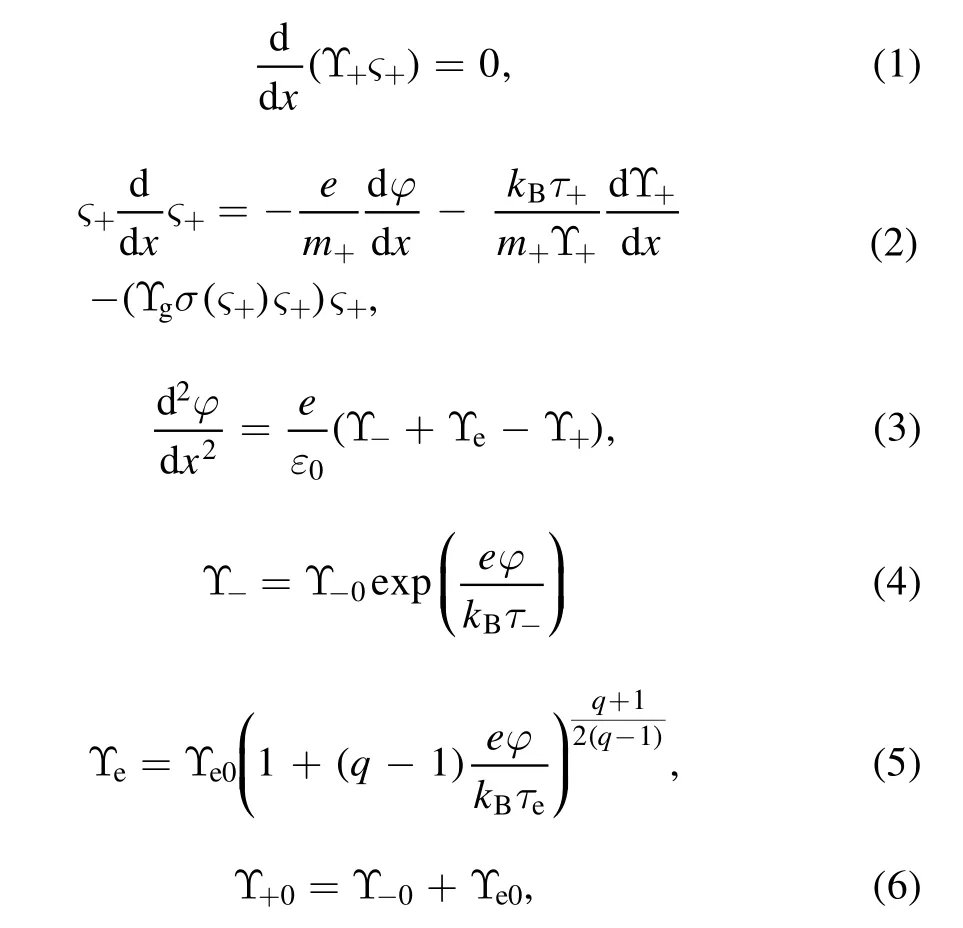
whereΥ+,ς+,m+andτ+are the density,velocity,mass and temperature of the positive ions,respectively.Υ−,ΥeandΥgare the densities of negative ions,electrons and neutrals,respectively.Υ+0,Υ−0andΥe0are the background densities of the positive ions,negative ions and electrons,respectively.τ−andτeare the temperatures of the negative ions and electrons,respectively.φis the electric potential andeis the electronic charge.qdefines the non-extensivity of the system andσ(ς+)is a momentum-transfer collisional cross-section,which has power-law dependence on the velocity of the positive ions and is given by

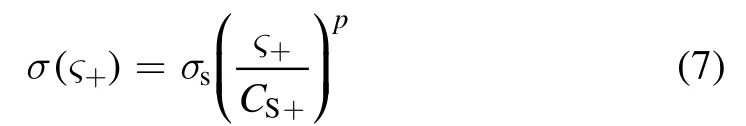
We have considered the case of the constant mean free path or constant collisional cross-section,i.e.p=0.Equations(1)-(7)are normalized with the help of the following dimensionless parameters

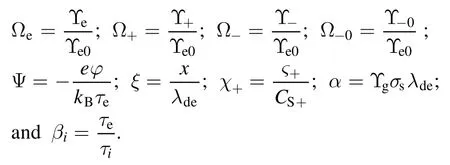
where Ω+0is the electropositivity,i.e.background density ratio of the positive ions to electrons of the system.The prime(′)and double prime(″)depict the first and second-order derivates,respectively,with respect toξ.

3.Boundary conditions and modified Bohm’s criterion

Equations(10)and(13)are coupled differential equations which will be solved with the help of appropriate numerical methods.In this paper,we have adopted the Runge-Kutta(RK)method of fourth-order.We must enumerate the initial conditions to apply the RK method on the given problem.The starting point of the numerical integration is assumed at the sheath edge,i.e.ξ=ξ0=0 and the numerical integration would terminate at the point of zero electron density.The wall/probe position,i.e.ξ=ξPis located at the point of zero electron density.The distance between the sheath edge and the wall/probe position is designated as the sheath thickness,i.e.ξ0−ξP.The initial value of the normalized electric potential at the sheath edge is assumed approximately equal to zero,i.e.ψ0=0.0001.However,the initial value of the normalized electric field at the sheath edge is assumed to nonzero to avoid the divergence of the numerical solutions,i.e.=0.1 is chosen.The allowed values of the positive ion velocity at the sheath edge,i.e.χ+0for a given set of parameters is calculated using the Sagdeev potential approach.Using the Sagdeev potential approach,the expression for the allowed values ofχ+0is determined as

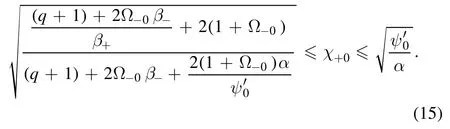
Forτ+→ 0 ⇒β+→ ∞,equation(15)appears as

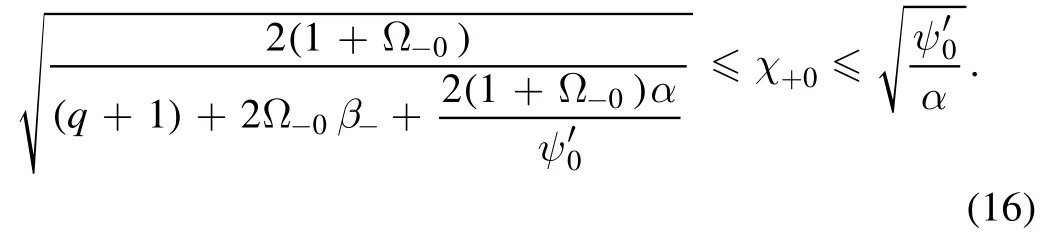
This is agreeing with the results of Borgohain and Saharia[13].

For Ω−0→0,equation(15)looks as

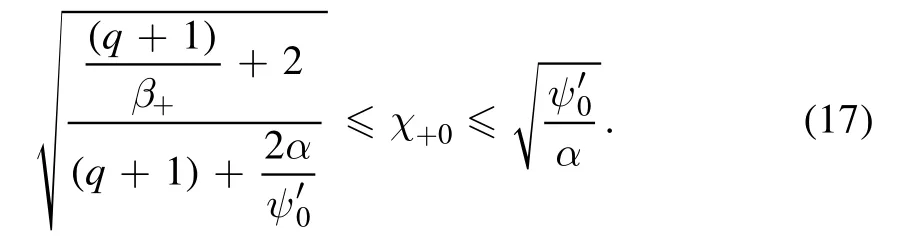
This is agreeing with the results of Hatami[50].

For Ω−0→0 andα→0,equation(15)appears as

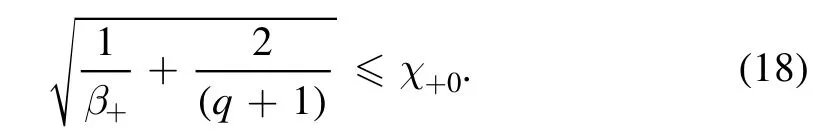
For Ω−0→0,α→0 andτ+→ 0 ⇒β+→ ∞,equation(15)appears as

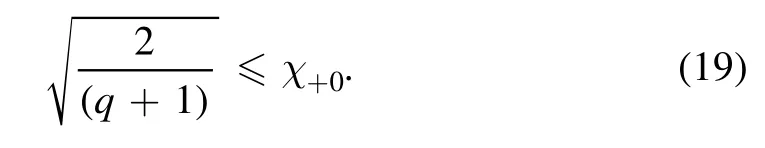
This is agreeing with the results of Tribeche et al[51]and Gougam and Tribeche[52].

For Ω−0→0,α→0,τ+→ 0 ⇒β+→ ∞andq→ 1,equation(15)appears as

This is agreeing with the results of Chen[53].

4.Results and discussions

The behaviour of the minimum allowed values of positive ion velocity at the sheath edge,i.e.χ+0 ,as a function of nonextensive parameter(q)for different collisional parameterα(figure 1(a)),electronegativity Ω−0(figure 1(b)),negative ion temperatureβ−(figure 1(c)),and positive ion temperatureβ+(figure 1(d)),is portrayed in figure 1.A significant reduction inχ+0with an increased Ω−0,β−andβ+is observed.Also,a minuscule reduction inχ+0is detected with the increasedαandq.From figure 1(a),we can conclude that in the collisional environment,positive ions can enter in the sheath regime even at lower velocities than the usual Bohm velocity.Figure 1(b)validates the fact that the negative ions help positive ions to get in the sheath regime.The temperature of electrons is appearing in the collisional parameter through the definition of the Debye length.In our study,the electron temperature is assumed to be constant and in order to see the effect of electron-to-positive(negative)ion temperature ratioβ+(β−),we have varied the corresponding ion temperature and kept the other parameters fixed.We have seen the effect of non-extensive and collisional parameters just by changing their values(one at a time)and keeping all the other parameters fixed.Therefore,in our study with constant electron temperature and varying ion temperature,qandαdo not change with the temperature of electrons,positive ions and negative ions.This also explains the almost linear behaviour of the minimum allowed value of the positive ion velocity(χ+0)at the sheath edge withqandαin figure 1(a).The value ofχ+0is reduced from 0.469 to 0.369 with an increased collisional parameter(α)from 0 to 0.5.With an increase in the collisional parameter,the percentage reduction inχ+0is observed to be reduced,i.e.,the effect of collision on the variation of Bohm velocity is more prominent for lower values ofα.The magnitude ofχ+0cannot continue to decrease because of the upper limit of the positive ion velocity at the sheath edge(please see equation(15)).This behaviour is in agreement with the results of other researchers also[13,54].

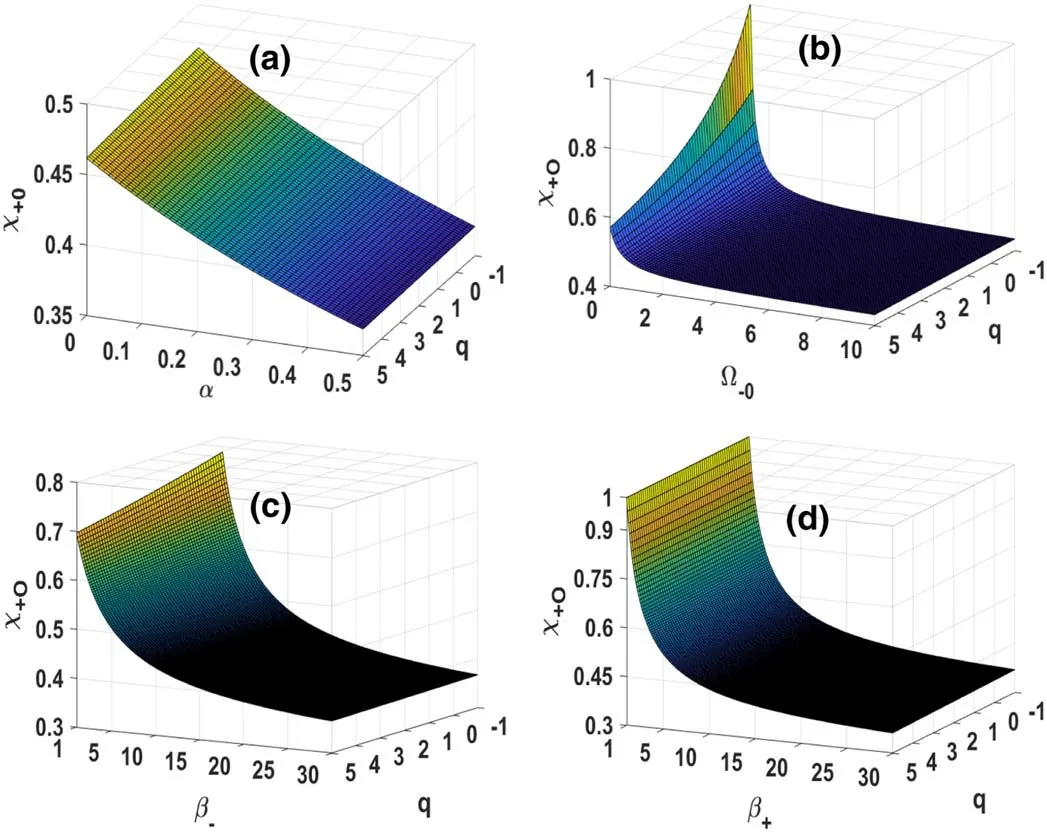
Figure 1.Behaviour ofχ+0 as a function of the non-extensive parameter(q)for(a)different values of the collisional parameter(α)when and β−=10;(b)for different values of electronegativity(Ω−0)whenand β−=10;(c)for different values of negative ion temperature(β−)whenand Ω−0=5; and(d)for different values of positive ion temperature(β+)whenand Ω−0=5.

The distribution of all the charged species densities,i.e.positive ions,negative ions and electrons,in the sheath regime is depicted in figures 2(a)and(b)for different positive ion temperature(β+).The densities of negative species are reduced with a considerable rate and approximately approach to zero near the probe/wall position.This is due to a negatively biased probe/wall.Moreover,because of the higher mass of the negative ions,their density is reduced approximately to zero even at a significant distance from the wall/probe position towards the sheath edge.Higher density of the positive ions is found near the probe for the increased value ofβ+.Also,the sheath of larger thickness is formed for higher value ofβ+.This is due to almost perfect shielding of the probe surface/voltage for lowerβ+values.

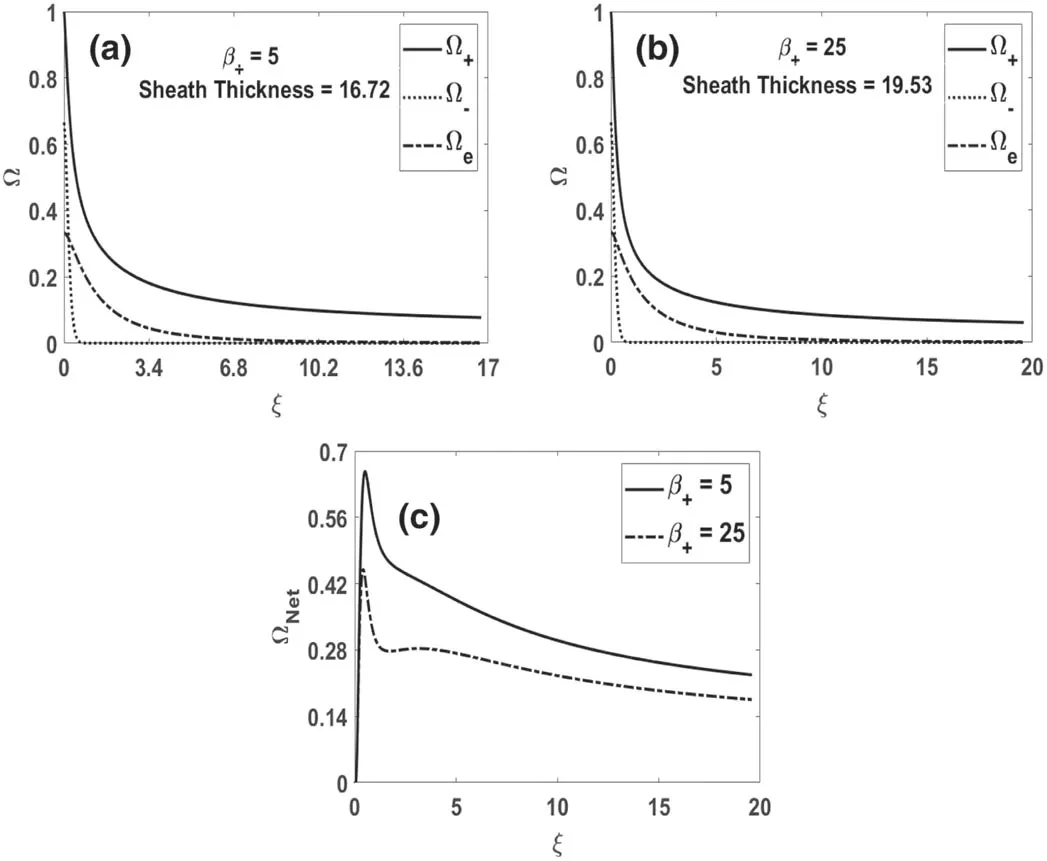
Figure 2.Behaviour of charged species densities,i.e.Ω+,Ω−and Ωe as a function of distance from the sheath edge to probe/wall position for different values of(a) β+=5 and(b) β+=25 when=0.1,α=0.1, β−=10, q=0.5 and Ω−0=2.Behaviour of net space charge density,ΩNet(c)as a function of distance from the sheath edge to probe/wall position for different values of β+ with the similar aforesaid parameters.

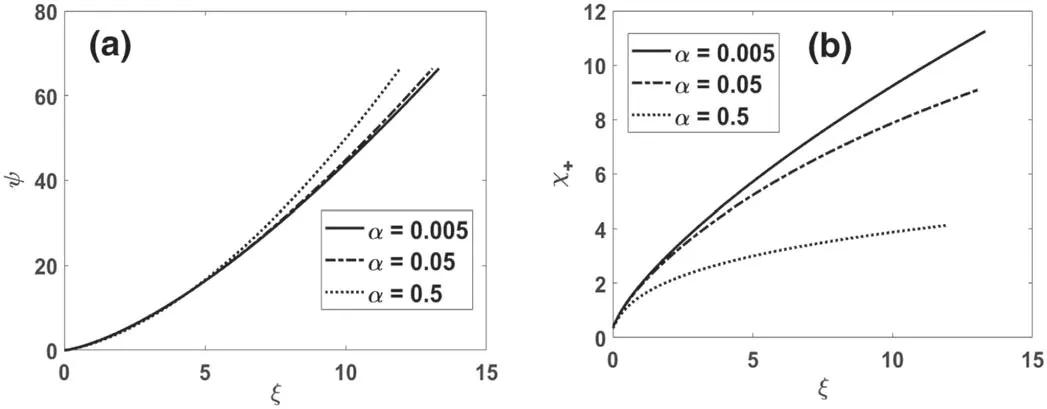
Figure 3.Behaviour of(a)electric potential(ψ)and(b)positive ion velocity(χ+)as a function of distance from the sheath edge to probe/wall position for different values of collisional parameter(α)when=0.1, β−=10, β+=15, q=0.5 and Ω−0=5.

The profile of net space charge density(ΩNet=Ω+−Ω−−Ωe)for different electron-to-positive ion temperature ratio(β+)is also seen in figure 2(c).The positive magnitude of ΩNetindicates that the sheath is composed of the majority of the positive ions.For both the values ofβ+=5 and 25,a steep rise and then the reduction in the space charge density are seen.This nature of the graph can be understood as follows.In the proximity of the sheath edge,a peak is appeared which is the main characteristic of the sheath regime;positive ions might accumulate here in a huge number.Then the net charge decreases due to the presence of some negative ions and electrons.Since the ions become more energetic for their higher temperature and can reach near the probe in higher number,the magnitude of the net space charge is expected to increase,which is the case in the figure(compare the cases withβ+=5 and 25).Since the positive ion flux is an invariant quantity(please see equation(9)),the number density of these ions,a little away from the peak region,decreases due to their acceleration(higher velocity)into the sheath regime.Hence,for the higher temperature of the ions,here the space charge decreases and also a dip in the net charge occurs as a result of imbalance of the pressure gradient,collisional and accelerating forces.

The profiles of the electric potentialψ(figure 3(a))and the positive ion velocityχ+(figure 3(b))for different collisional parameterαare shown in figure 3.With an increase inα,the number of collisions between positive ions and neutrals is also increased and so the energy loss.Therefore,the energy gain by the positive ions as they move toward the probe/wall surface is relatively lesser for higherα.The magnitude ofψis increased with a slightly rapid rate for higherα.Also,a lower sheath thickness is recorded for higherα.

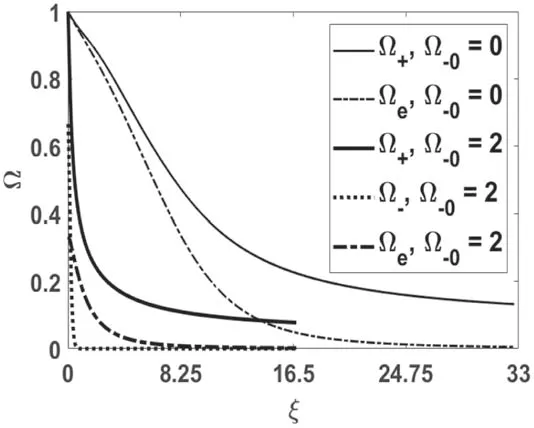
Figure 4.Comparative study of charged species densities as a function of distance from the sheath edge to probe/wall position for electropositive(thin lines)and electronegative plasma(thick lines)when=0.1, β−=10, β+=5, q=0.5 and α=0.1.Here,Ω−0=0 corresponds to electropositive plasma.

A comparative study of the charged species densities for electropositive and electronegative plasma is depicted in figure 4.Here,Ω−0=0 and Ω−0=2 correspond to the cases of electropositive and electronegative plasmas,respectively.The densities of the charged species are reduced with a considerable rate in the case of electronegative plasma,whereas for the case of electropositive plasma,sheath thickness of higher magnitude is resulted.

We can discuss the validity of the range of electron-tonegative ion temperature ratio β−keeping in mind the experimental studies of Ghim and Hershkowitz[41]who investigated a low-pressure electronegative plasma(Ar-O2)through Langmuir probe.They observed the Boltzmann distribution of the negative ions for the temperature range of 0.06±0.02 eV with the resulting parameters ne=3.8×109cm−3and Te=0.69 eV.Corresponding to this experimental data,the temperature ratio β−in our calculations lies in the range of 8.625-17.25.In figures 2-4,the value of β−was chosen as 10,which lies in the desired range obtained experimentally.On the other hand,Borgohain and Saharia[13]have considered the range 0＜β−＜20 in electronegative plasma with q non-extensive electrons and cold positive ions.In order to further explore the process,we had chosen the range 1＜β−＜30 only in figure 1.This might be justified for the low-pressure plasmas,where the temperatures of ions and electrons less than 1 eV(with electron temperature even a little more than 1 eV)are generally attained for both the cases,i.e.when negative ions have similar and miniatured temperature in comparison to that of the electrons.Since we discussed all the results keeping β−=10,the conclusions drawn in the manuscript are well-meant.

In the present theoretical model,the sheath thickness has been normalized with the Debye length(λde).In un-normalized form,for collisional electronegative plasma,the sheath thickness has been calculated and found to be of the order of 1.26 mm for the non-extensive distributed electrons and of the order of 0.217 mm for the Boltzmann distributed electrons.For collision-less electronegative plasma,the sheath thickness amounts to 1.3 mm and 0.222 mm for the non-extensive distributed electrons and the Boltzmann distributed electrons,respectively.The sheath of 0.5 mm thickness is found to be formed for the Boltzmann distributed electrons in collision-less plasma that does not have negative ions(electropositive plasma).Han et al[55]have experimentally determined the sheath thickness of the order of 0.36 mm for the electropositive plasma.Hence,the calculated values of the sheath thickness based on our modelling and the experimental value are close.

The magnitude of the Debye length will reduce with an increment in the plasma density,this in turn results in the reduction of the magnitude of the sheath thickness.In our theoretical model,when the plasma density is increased from 2.5× 1010to 9.5× 1010cm−3,the value of the sheath thickness is found to be reduced from 1.26 to 0.64 mm for the non-extensive distributed electrons,whereas 0.217 to 0.11 mm for the Boltzmann distributed electrons.Consistent to our observation,Han et al[55]also have experimentally determined the reduction in the value of the sheath thickness from 0.36 to 0.28 mm when the plasma density was increased from2.5× 1010to9.5× 1010cm−3.

We can discuss qualitatively the effect of temperature gradient(spatial variation of the temperature of charged species)on the sheath formation.The behaviour of the sheath is expected to be modified once we consider the temperature gradient.For example,we may observe more dips in the net space charge profile(figure 2(c))and also the sheath thickness may vary.However,the effect of temperature gradient on the sheath thickness may not be significant in view of the smaller temperature-gradient-driven drift(force)in comparison to the one driven by pressure-gradient/thermal pressure.

Finally,this is worth mentioning that our results shall play an advantageous role in plasma systems where the temperature of the positive ions and the presence of collisions between the ions and neutrals have a significant effect on the sheath formed at material’s surface; hence,the plasma processing and plasma-surface interaction can be understood.These results will also be beneficial in the plasma systems like fusion[56]and astrophysical plasmas where the distribution of the particles is far away from their usual Boltzmann distribution.

5.Conclusions

The dependence of minimum allowed positive ion velocity at the sheath edge(for the formation of sheath)on the positive and negative ion temperatures,electronegativity,collisional parameter and non-extensivity was understood.When collisions between the positive ions and the neutrals are considered,then these ions are found to enter in the sheath regime even at lower velocities than the usual Bohm velocity,which means the Bohm’s criterion is modified.The sheath thickness is reduced with an increment in the temperature of the positive ions and the collisional parameter.The energy gain by the positive ions during their movement towards the probe/wall position is relatively lesser for the case of higher collisional parameter.The distribution of all the charged species densities for the cases of electropositive and electronegative plasma was also compared and noteworthy modifications were observed,proving the role of negative ions in plasmasurface interaction process.

Acknowledgments

Rajat Dhawan acknowledges the Council of Scientific and Industrial Research(CSIR),Government of India for providing financial support(Grant Reference Number:09/086(1289)/2017-EMR-1).