High harmonic generation driven by twocolor relativistic circularly polarized laser pulses at various frequency ratios

Duan XIE(谢端),Yan YIN(银燕),Tongpu YU(余同普),Hongyu ZHOU(周泓宇),Ziyu CHEN(陈自宇)and Hongbin ZHUO(卓红斌)

1 School of Electronic Information and Electrical Engineering,Changsha University,Changsha 410003,People’s Republic of China

2 Department of Physics,National University of Defense Technology,Changsha 410073,People’s Republic of China

3 College of Physics,Sichuan University,Chengdu 610064,People’s Republic of China

4 Center for Advanced Material Diagnostic Technology,Shenzhen Technology University,Shenzhen 518118,People’s Republic of China

Abstract High harmonic generation(HHG)by two-color counter-rotating relativistic laser pulses with arbitrary frequency ratio is investigated through particle-in-cell simulations.It is shown that the dichromatic laser driver at various frequency ratios can effectively produce high-order harmonics with different spectral features.A general selection rule of this extended scheme can be obtained and the corresponding harmonic helicity can be identified through a simple analytical model based on a relativistic oscillating mirror.Thus,the results in this paper may offer new opportunities for arbitrary spectral control of generated harmonics,which is of significance for diverse potential applications in practice.

Keywords:high-harmonic generation,two-color laser pulses,relativistic oscillating mirror

1.Introduction

Generation of high-bright,ultrashort light pulses in the extreme-ultraviolet(XUV)or soft x-ray region provides exciting opportunities to ultrafast science,allowing real-time observation of a broad range of ultrafast phenomena,e.g.,the fast electron dynamics on the atomic scale[1-12].In particular,significant progress on the radiation source has been made over the past few years.In addition to free electron lasers(FELs)[13,14]and laser-gas based harmonics[15,16],high-order harmonic generation(HHG)from relativistic laser interaction with over-dense plasmas has also attracted considerable interest for its potential to produce attosecond pulses on the table-top scale with high brilliance.Up to now,at least three mechanisms have been identified to be responsible for the laser-plasma based HHG process,i.e.,coherent wake emission(CWE)[17,18],relativistically oscillating mirror(ROM)[19-30]and coherent synchrotron emission(CSE)[31-33].Among them,ROM model acts as one of the most common and robust in the relativistic regime.When a relativistic laser pulse irradiates a solid target,the target’s surface will instantaneously be fully ionized into over-dense plasmas(known as plasma mirrors),whose electrons oscillate relativistically due to the combined action of ponderomotive force and charge-separation electrostatic force.The reflected pulse contains high-order harmonics resulted from the relativistic Doppler effect.It is shown that the ROM has long been believed invalid when a single circularly polarized laser pulse is employed at normal incidence because the laser ponderomotive force contains only slowly varying components following the pulse envelope,which is unable to drive the plasma surface oscillation effectively.However,the situation changes for two-color laser fields.In particular,two-color counter-rotating circularly polarized laser pulses composed of fundamental frequencyω0and its second harmonic2ω0have been proven effective in gas-HHG process[34-37]and also in laser-plasma based HHG process[38,39].The advantages of two-color scheme own two aspects:on one hand,it can efficiently produce circularly-polarized harmonics and attosecond pulses in ultra-violet or soft x-ray region,which are important for probing chiral structures and dynamics.On the other hand,it can selectively enhance the group of harmonic orders,i.e.,n=3m±1(m=1,2,3···),owing to symmetry requirements of the interaction system[36,38].Despite considerable investigation into the two-color HHG scheme,there are still some problems to be clarified:can it be extended to use dichromatic laser pulses with various frequency ratios in the relativistic regime?Which frequency ratio can produce higher HHG conversion efficiency?Is it possible to establish a general selection rule?

To shed light on these questions,we further investigate the two-color laser scheme of relativistic HHG within a broader range of frequency ratios by use of numerical simulations and theoretical analysis based on work by Chen[38].On one hand,counter-rotating dichromatic pulses withω0+ 2ω0,ω0+ 3ω0,ω0+ 4ω0and2ω0+3ω0frequency components are considered in two-dimensional(2D)particlein-cell(PIC)simulations.The results show that circularly polarized harmonics with high efficiency and different harmonic orders can be generated with different laser configurations.On the other hand,we develop a simple model based on the ROM to interpret the general selection rule of HHG,which can predict the harmonic spectral features by driving lasers with arbitrary frequency ratios and are in excellent agreement with the PIC simulations.

2.PIC simulations

We first investigate the HHG process via the two-color laser scheme at various laser frequency ratios by use of the 2D3V(two spatial,three velocity dimensions)EPOCH code[40].Two counter-rotating driving pulses with different frequencies impinge the plane target from the left side.The total electric field can be expressed as:

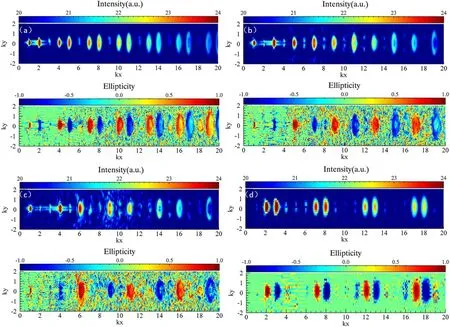
Figure 2.The intensity and corresponding ellipticity distribution of generated harmonics versus kx and ky in frequency domain at different frequency ratios:(a) ω1=ω 0,ω2=2ω 0,(b) ω1=ω 0,ω2=3ω 0 ,(c) ω1=ω 0,ω2=4ω 0,(d) ω1=2ω 0,ω2=3ω 0.

Here,we consider the two-color laser pulses with four different frequency ratios:(1)ω1=ω0,ω2=2ω0,(2)ω1=ω0,ω2=3ω0,(3)ω1=ω0,ω2=4ω0,and(4)ω1=2ω0,ω2=3ω0.The Lissajous fgiures of the superposed electric feilds are displayed in figures 1(a)-(d).From figure 1,one can see that in the case ofω0+ 2ω0andω0+ 3ω0,the corresponding Lissajous figures show threefold and fourfold symmetries respectively.In the case ofω0+ 4ω0and2ω0+3ω0,although the details of the Lissajous figures are different,they exhibit the same fivefold symmetry.

Then,we investigate the different harmonic features of the four cases,which are closely related to the various symmetries of their superposed electric fields.The intensity and ellipticity distribution of the high harmonics at each frequency ratio are shown in figures 2(a)-(d).Here,the ellipticity of emitted harmonics ε can be acquired as follows:first,we perform a Fourier transform of the two electric filed components of generated harmonics:E y(f)=FFT(Ey),Ez(f)=FFT(Ez),where f is the frequency of harmonics,E y,Ezare the strength of the harmonic feild along the direction y,z,respectively.Then,the ellipticity of generated harmonics can be calculated byIn this equation,From fgiure 2(a),in the case ofω1=ω0,ω2=2ω0,we see only the harmonics with orders ofn=3m±1(m=1,2,3···)being produced,while every third one is missing.Besides,all of the harmonics emitted are nearly circularly polarized(ε≈±1),and the handedness of 3m+1 harmonics(4ω0,7ω0,10ω0...)is consistent with that of the fundamental field,while the helicities of3m−1 harmonics(2ω0,5ω0,8ω0,11ω0...)are the same as that of the double-frequency field.These results are consistent with the previous reports[38],showing the reliability of our simulations.

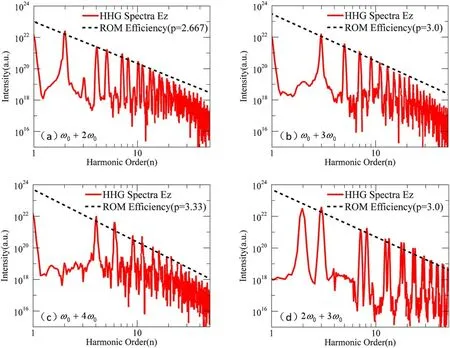
Figure 3.The harmonic spectra of the reflected pulse and corresponding conversion efficiency at different frequency ratios:(a) ω1=ω 0,ω2=2ω 0 ,(b) ω1=ω 0,ω2=3ω 0 ,(c) ω1=ω 0,ω2=4ω 0 ,(d) ω1=2ω 0,ω2=3ω 0.

For the other three cases in figure 2,similar conclusions can be drawn.Figure 2(b)shows the results withω1=ω0,ω2=3ω0.Only harmonics withn=4m±1(m=1,2,3···)are generated,while the other frequencies are absent.In addition,harmonics with4m+1 and4m−1 orders are co-rotating with the fundamental and3ω0driving pulses respectively.Figure 2(c)shows that harmonics withn=5m±1(m=1,2,3···),where the polarization states of5m+1 harmonics are consistent with that of the fundamental field,while those of5m−1 ones are the same as the4ω0laser.Figure 2(d)demonstrates driving lasers withω1=2ω0,ω2=3ω0can result in harmonics withn=5m+2,5m+3(m=1,2,3···),and the chirality of 5m+2,5m+3 harmonics are consistent with that of the2ω0and3ω0field,respectively.

Figures 3(a)-(d)show the harmonic spectra with fitted scalings for the four different frequency ratio cases.The black dash line ftis the spectra roll-off byI(n)∝n−p,where n is harmonic order and p is the fitting coefficient.From these results,we may find that which frequency ratio may produce the highest HHG conversion efficiency.In the first case(figure 3(a)),the spectral intensity scaling of the harmonic orders is close toI(n)∝n−8/3,the same with that analytically derived for HHG by linearly-polarized driving lasers via ROM[22].From figures 3(b)-(d),one can get that the fitting coefficients p are 3.0,3.33,3.0,respectively,which means that the HHG conversion efficiency is the highest when the frequency ratio is 1:2 and will be slightly lower as it is changed.Nevertheless,the results show that the extended dichromatic scheme at other frequency ratios can be still efficient enough in the harmonic generation.

Figure 4 displays the three-dimensional waveforms of the electric fields of a group of neighboring harmonics(n=11,14)in the third case ofω1=ω0,ω2=4ω0.From the two panels,we can clearly see that the neighboring harmonics are both nearly circularly polarized but with opposite handedness.Specifically,the helicity of the 11th harmonic corresponds to that of the fundamental driving field,while the helicity of the 14th harmonic is the same as that of the4ω0one.

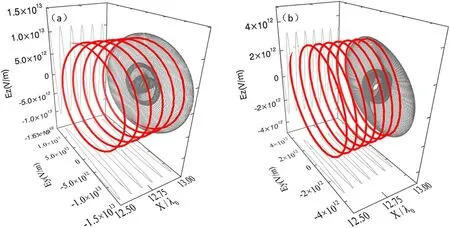
Figure 4.Three-dimensional electric field waveforms of the(a)11th and(b)14th harmonic in the case of ω0+ 4ω 0.

3.Theoretical analysis

To explain the simulation results above,we develop a simple model based on the ROM.When a relativistic laser pulse irradiates the surface of over-dense plasmas,the electrons near the surface boundary are driven by the superposition field of the incident and reflected beams.Inside the plasma,the electro-magnetic field decays rapidly over a distance of the skin depth.The motion equation of an electron near the plasma boundary can be expressed as[41]:

where m and e are electron’s mass and charge,E and B represent the total electric and magnetic fields,v is the electron velocity,γ(t)=(1−v2/c2)−1/2is the relativistic factor of electrons andωpis the plasma frequency.Equation(2)can act as the starting point of our theoretical model.

We consider the counter-rotating dichromatic laser pulses normally incident along the x axis,and thus the electric and magnetic fields of the two laser pulses can be written as E1=E1cos(ω1t)ey∓E1sin(ω1t)ezandB1=B1cos(ω1t)ez±B1sin(ω1t)ey,respectively,whereω1andω2represent each laser frequency(ω1≠ω2).Then,the tangential component of the Bt=2E/candEt=ζ(Bt×x),whereζis the plasma magnetic field and the electric field can be acquired as impedance[40].The total electromagnetic field on the target surface can be expressed by+ω2E2sin(ω2t)]ey+[ω1E1cos(ω1t)−ω2E2cos(ω2t)]ez}and−E2cos(ω2t)]ez}.Substituting the expressions above into equation(2),we can obtainand.

To proceed,we use the iteration method for the analytical derivation[41].At the first step,the relativistic factor γ is assumed to be invariant with time t; x,and ˙xare both considered equal to zero.Then all the second order quantities are sufficiently small and can be reasonably neglected.According to the assumptions,the motion equations of surface electrons along three orthogonal directions can thus be simplified to:

By iterating the expressions ofand,we can obtain the expressions ofand.Then,substituting them into the expression of,we have

Equation(4)shows that counter-rotating dichromatic pulses drive the surface electrons(plasma mirror)oscillating at the frequency ofω1+ω2.According to the ROM model,the periodic oscillation of the plasma mirror may induce a phase modulation of the reflected wave[20,21].We thus assumex(t)=x0sin[(ω1+ω2)t]to be the displacement of the relativistic mirror surface in the x direction,then the phase shift of the reflected wave resulting from this displacement can be obtained as:φ(t)=φ0sin[(ω1+ω2)t].Therefore,the reflected electric field can be approximately expressed as[21]:

In equation(5),the well-known Jacobi expansion is used,whereJmis the Bessel function.

Through one dimensional Fourier transform of the reflected electric field with respect to time,the reflected harmonic spectrum can be expressed as:

From equation(6),we see that two series of circularly-polarized harmonics with the frequencies of(m+1)ω1+mω2and(m+1)ω2+mω1can be produced.Harmonics with the frequencies of(m+1)ω1+mω2have the same helicity as theω1driving pulse,while those with(m+1)ω2+mω1co-rotate with theω2pulse.This result serves as a general selection rule of the two-color scheme at various frequency ratios.

Now we apply the abovementioned general rules to the four specific cases considered in the PIC simulations:for the first case,the expression of the reflected harmonic spectrum becomes{δ[ω−(3m+1)ω0]eL+δ[ω−(3m+2)ω0]eR},which shows that in the frist case,the plasma surface oscillates at3ω0.Consequently,only harmonics of3m±1 can be produced.Among them,the3m+1 harmonic orders have the same helicity as the fundamental field,the3m−1 orders co-rotate with the2ω0field,while the3morders are absent,in consistent with the previous results and fgiure 2(a).Forω1=ω0,ω2=3ω0,equation(6)becomeswhich indicates that the4ω0oscillation of the plasma mirror can generate harmonics with4m±1 orders.In addition,harmonics with4m+1 and4m−1 orders are co-rotating with the fundamental and3ω0driving pulses,respectively.Forω1=ω0,ω2=4ω0,we can getwhich implies that the two pulses with this frequency ratio will drive the plasma mirror oscillating at5ω0.Thus harmonics with 5m±1 can be produced,and the polarization states of5m+1 harmonics are consistent with that of the fundamental field,while those of5m−1 ones are the same as the4ω0laser.These agree well with the results in figure 2(c).Finally,we consider the case of{δ[ω−(5m+2)ω0]eL+δ[ω−(5m+3)ω0]eR}.In this case,the plasma surface will also oscillate at5ω0,and result in harmonics with5m+2,5m+3 orders.Similarly,the chirality of5m+2,5m+3 harmonics are consistent with that of the 2ω0and3ω0feild respectively,well supporting the numerical results of figure 2(d).

Other than these four specific cases,when dichromatic laser pulses with other frequency ratios are used,the corresponding selection rules and polarization states of the generated harmonics can also be obtained from equation(6).

4.Conclusions

In summary,we have investigated the HHG process from two-color counter-rotating relativistic laser pulses with various frequency ratios interaction with over-dense plasmas.From the PIC simulation results,we find that combining driving lasers with different frequencies and opposite handedness can efficiently generate ultra-intense circularly polarized high-order harmonics,the orders of which can be selectively enhanced by changing the frequency ratio of driving lasers.The underlying mechanisms can be understood by an extended theoretical model based on ROM.This scheme extends the scope of spectral control of high harmonics from relativistic plasmas and provides an alternative to produce attosecond circularly polarized XUV/x-ray pulses,which may have broad application prospects in various scientific fields.In addition,to find out the optimal combination of frequency ratio for HHG,optimization algorithm,e.g.,genetic algorithm(as used in[42])may be employed in the future work.

Acknowledgments

This work is supported by the National Key R&D Program of China(No.2018YFA0404802),Science Challenge Project(No.TZ2016005),National Natural Science Foundation of China(Nos.11774430,11875319),Research Project of NUDT(Nos.ZK18-02-02),Fok Ying-Tong Education Foundation(No.161007),the Fundamental Research Funds for the Central Universities(YJ202025),the Natural Science Foundation of Hunan Province(Nos.2020JJ5614 and 2020JJ5624)and the Scientific Research Foundation of Hunan Provincial Education Department(No.20A042).We would like to thank the National Supercomputing Center in Guangzhou(NSCC-GZ)for providing their computing facilities.