非简谐势阱超冷原子气体中涡旋的形成
2021-04-21马娟
马娟


摘 要:1995年,玻色-愛因斯坦凝聚(BEC)的实现证实了物质第五态的存在。玻色-爱因斯坦凝聚体是一种新的宏观量子态物质,它是一种长程相干的物质,具有超强相干性和超流性。通过激光扰动,人们会在超冷原子气体中发现涡旋的产生。所以,研究超冷原子气体的涡旋性质对于认识冷原子气体的超流特性有深远的意义。本文主要研究了冷原子气体中两体相互作用及势阱的非简谐性对系统模频率及单核涡旋产生的影响。
关键词:非简谐;超冷原子;涡旋
中图分类号:O469文献标识码:A文章编号:1003-5168(2021)02-0127-03
Formation of Vortex in Ultra-cold Atomic Gases Confined in Anharmonic Potential Trap
MA Juan
(Xinhua College of Ningxia University,Yinchuan Ningxia 750021)
Abstract: In 1995, the realization of Bose-Einstein Condensation (BEC) confirmed the existence of the fifth state of matter. Bose-Einstein condensate is a new macroscopic quantum state matter, which is a long-range coherent matter with super-strong coherence and superfluidity. Through laser perturbation, people can find vortices in the ultra-cold atomic gas. Therefore, studying the vortex properties of ultra-cold atomic gases has far-reaching significance for understanding the superfluid properties of ultra-cold atomic gases. This paper mainly studied the influence of the two-body interaction and the anharmonicity of the potential trap in the ultra-cold atomic gases on the system mode frequency and the single-nuclear vortex.
Keywords:anharmonic;ultra-cold atomic;vortex
早在1924年,印度物理学家萨蒂延德拉·纳思·玻色预言了在原子温度非常低时,玻色原子气体将会在系统的最低能量态上凝聚。直至1995年,美国科罗拉多大学实验天体物理联合研究所(JILA)的埃里克·科内尔等人才利用先进的激光冷却和蒸发冷却的技术率先在试验上实现了玻色爱因斯坦凝聚(BEC)。至此,人们研究BEC系统的技术瓶颈被打破,对于玻色-爱因斯坦凝聚体的试验探索揭开了BEC神秘的面纱,人们可以直观地观测该凝聚体,并对该凝聚体的各种性质进行探索。
物理学家利用不同的技术手段形成了各种类型的势阱(光晶格、简谐势阱、非简谐势阱、煎饼状和墨西哥帽状)囚禁超冷原子气体,研究它在不同势阱中的相变、物质波传播、量子计算、Bloch振荡和隧穿效应等特点[1-3]。通过对液氦凝聚体的研究,物理学家发现了玻色-爱因斯坦凝聚的超流性质,这种超流特性体现在它的无耗散性、无旋性,并能支持持续流等。W Ketterle小组用蓝失谐的激光束搅动玻色-爱因斯坦凝聚体,发现搅动速度达到一临界值时就会有耗散产生,因为激光束的运动速度超过临界值,使得它在运动方向上的局部流体速度超过声速,导致超流体中产生涡旋对。然而,这种涡旋对的产生直接在试验上证实了气态玻色-爱因斯坦凝聚体的超流性质。本文将从玻色-爱因斯坦凝聚体系统出发,研究势阱的非简谐性及系统中两体排斥相互作用对玻色-爱因斯坦凝聚体的模频率及产生单核涡旋的临界频率的影响。
1 模型
在低温下,只考虑玻色-爱因斯坦凝聚体中的两体相互作用,则BEC系统的动力学行为可以利用含时的GP方程描述[4-6]:
[ih?ψ(r,t)?t=-h22m?2+V+gψ(r,t)2-Ω0Lzψ(r,t)](1)
式中,[g]为原子间两体相互作用的物理量,对于实验室的[87Rb]原子,[g=5h×10-11 cm3/s][6];[Lz]为轴向角动量算符;[Ω0]为势阱旋转频率;[V]为磁囚禁势。
[Lz=xpy-ypx] (2)
[V=12mω20[(x2+y2)+ε(x2-y2)+ω2zω20z2]+U0e-2r2w2] (3)
式中,[w]和[U0]根据实验室数据选定(光束腰[w]=25 μm,激光束强度[U0]约为1.242×10-30 J)[7]。
势阱的轴向频率为1 200 Hz,横向频率为120 Hz。根据限制条件[2rw<1],对于势阱,利用高斯势展开,则其可以表示为:
[U(r)=U0e-2r2w2~U0(1-2r2w2+2r4w4)] (4)
此时,势阱可以通过简化写为:
[V=12hω0[(x2+y2) (1-k)+ε(x2-y2)+ω2zω20z2+λ(x2+y2)2]](5)
式中,[k=4U0/mω20ω2];[λ=k(a0/ω)2];[x]、[y]、[z]是以谐振长度[a0](2.489 μm)为单位。
设[Z]方向的波函数是:
[ψz=(πaz)-0.5e-z2/2a2z] (6)
式中,[az=h/mωz]。
对式(1)中变量分离写出系统的拉格朗日密度,即
[ih2(ψ?ψ??t-ψ??ψ?t)+(h22m?ψ2+V(x,y)ψ2+g2ψ4-Ω0ψ?Lzψ)] (7)
式中,[g=g/2πaz]。
考虑准二维情况,采用如下试探函数[4-5]:
[ψ(X,Y,t)=C(t)e-0.5[α(t)X2+β(t)Y2-2iγ(t)XY]] (8)
式中,[C(t)]是归一化常量;[X=x/a0],[Y=y/a0],[a0]为谐振长度。
[C(t)]用公式可以表示为:
[C(t)=(ND/πa20)0.5] (9)
式中,[N]为原子总数;[D=α1β1-γ21];[a0=h/mω0]。
[α(t)=α1(t)+iα2(t)]、[β(t)=β1(t)+iβ2(t)]、[γ(t)=γ1(t)+iγ2(t)]是無量纲的复变量。将上述试探波函数代入拉格朗日密度方程中进行空间上的积分:
[LNhω0=14D{-(β1α2+α1β2+2γ1γ2)+(α1+β1)D+(α22+γ22)β1+(β22+γ22)α1+2(α2+β2)γ1γ2+(α1+β1)+λ(3α21+2α1β1+3β21+4γ21)2D+PD32+2Ω[γ1(α2-β2)+γ2(α1-β1)]}](10)
式中,[P]为两体相互作用的无量纲量,吸引还是排斥相互作用由s波散射波长决定。
[P]用公式可以表示为:
[P=22π(N-1)a/az] (11)
系统平衡态时的变分能量可以得出,即
[ENhω0=14[(α1+β1)+γ22(1α1+1β1)+(1α1+1β1)+λ2(3α21+2α1β1+3β21)+Pα1β1+2Ωγ2(1β1-1α1)]](12)
式中,[Ω=Ω0/ω0]。
通过对系统能量取极小值,得到平衡态下关于变分参量的变分方程,即
[α210(1+P2β10α10)=γ220-2Ωγ20+1+λ(3α10+1β10)β210(1+P2α10β10)=γ220+2Ωγ20+1+λ(3β10+1α10)γ20=Ω(β10-α10)(β10+α10)](13)
定义变量[η]满足式(14)条件,它描述了系统由于旋转引起的对称性破坏问题。
[η=
从变量的定义式可以看出,它取值为1时,系统中没有形变产生,也就不可能产生涡旋这一形态。理论上来说,当系统中有涡旋产生时,首先系统形状会发生变化,系统中原子因为外界的转动而获得能量时,系统中单粒子的平均角动量就会发生变化,单粒子的平均角动量为1时,系统中就会产生涡旋,这一结论早在试验上就有过记载和验证[8-9]。
单粒子平均角动量形式为:
[
由此可得,系统中产生单核涡旋时的临界频率为:
[Ωc=2η(α10+β10)/(1-η)2] (16)
2 模频率
令[α1=α10+δα1],[β1=β10+δβ1],[α2=δα2],[β2=δβ2],[γ2=δγ2],对系统的拉格朗日量进行展开,并保留展开式中的二阶项。因为势阱各向同性,则[δα1=-δβ1],令旋转频率为0,根据欧拉-拉格朗日方程,可以得到关于[δα1]和[δβ1]的耦合方程组,得出系统的四极模频率具有如下形式:
[δα1=[P2α210β10α10-4-2λ(9α10+2β10)]δα1- [P2α210α10β10+2λα10β210]δβ1δβ1=[P2β210α10β10-4-2λ(2α10+9β10)]δβ1- [P2β210β10α10+2λβ10α210]δα1] (17)
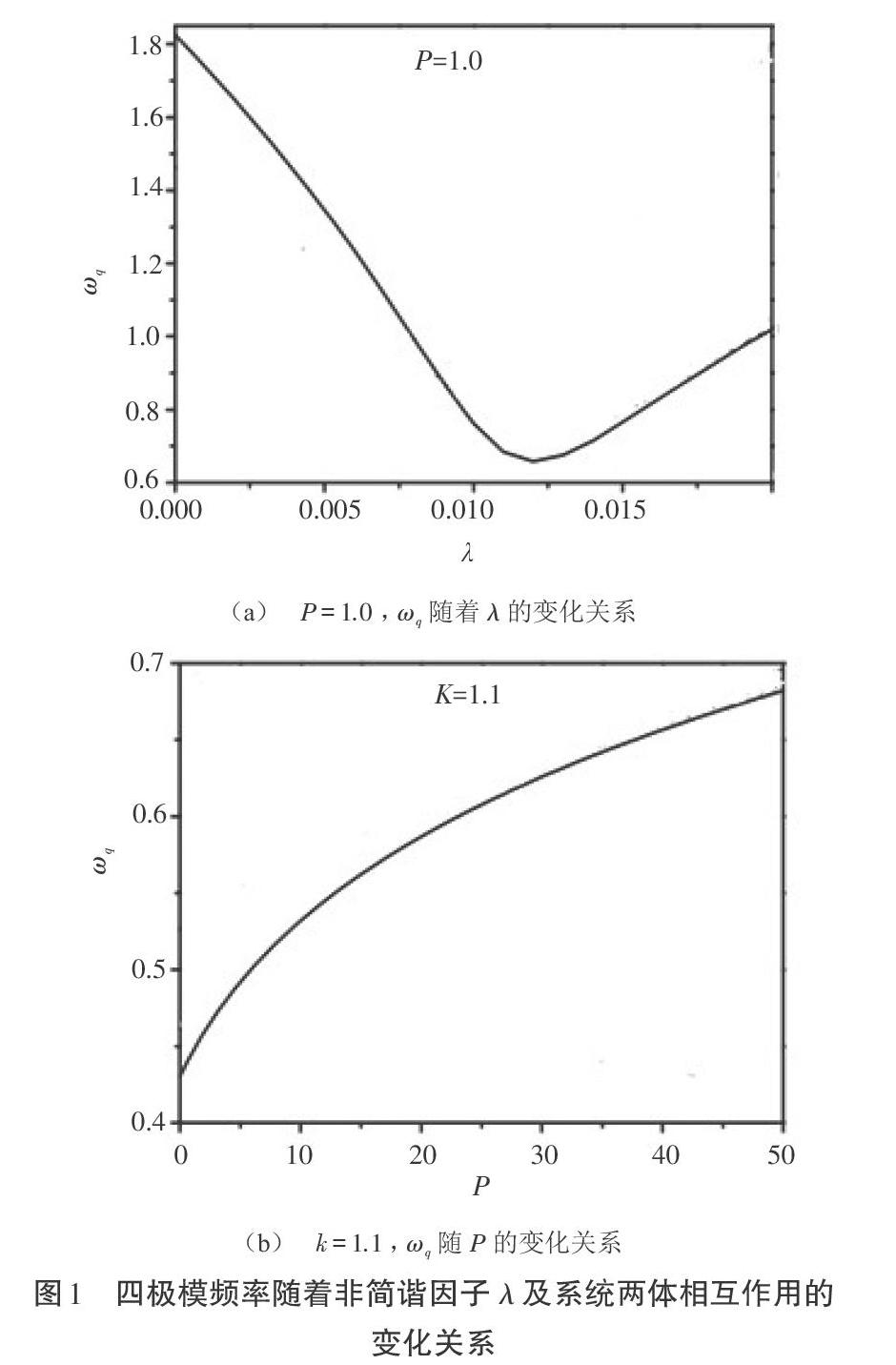
[ω2q=4(1-k)+20λR0-PR20] (18)
式中,[R0]为系统的平衡半径。
四极模频率[ωq]随着[λ]和[P]的变化关系如图1所示。图1(a)中,四极模频率[ωq]随着[λ]的增加而减小([λ<0.01(k<1)]),达到某一极小值后,即当[λ>0.01(k>1,墨西哥帽状)]时,则会出现增加的趋势。图1(b)给出[ωq]在墨西哥帽的势阱中随着两体排斥相互作用的增加逐漸增加。
3 涡旋的形成
利用平衡方程式(13),得到一个耦合多项式方程组,即
[(α310β310+2α410β210+α510β10)(1+P2β10α10)-α310β10(3Ω2-k+1)+(α10β310+2α210β210)(Ω2+k-1)-λ(5α210β10+7α10β210+α310+3β310)=0(α310β310+2α210β410+α10β510)(1+P2α10β10)-α10β310(3Ω2-k+1)+(α310β10+2α210β210)(Ω2+k-1)-λ(5α10β210+7α210β10+β310+3α310)=0] (19)
对于非简谐势阱,在只考虑系统中原子间的排斥相互作用时,它产生涡旋的临界频率随着非简谐因子[λ]的增加先减小后增加。当势阱形状是墨西哥帽时,临界旋转频率比较小,这表明此种情况下,系统慢速旋转就可以产生涡旋。在[k=1.1],[P]=1.0时,临界频率[Ωc]随[λ]的变化关系如图2所示。
4 结论
对于旋转束缚在非简谐势阱中的BEC系统,根据变分方法,将BEC系统的四极模频率计算出来,通过作图发现,在只考虑系统中原子间两体排斥相互作用时,四极模频率在非简谐因子[λ]增加的过程中逐渐减小至某一极小值后又会增加。当系统中[k>1]时,系统的模频率则会随着两体排斥相互作用的增加而增加。系统产生涡旋的临界旋转频率也有同样的变化图像。在只考虑两体排斥相互作用时,系统中临界涡旋频率随着非简谐因子[λ]先减小再增加,相较于一般势阱,非简谐势阱中发生形变进而产生涡旋更容易些,也就是给势阱一个小的旋转就会有涡旋产生。但是,当势阱深度越来越深,越来越紧时,产生涡旋的外界旋转频率则会增大。
参考文献:
[1]Bausmerth I,Recati A,Stringari S.Destroying Superfluidity by Rotating a Fermi Gas at Unitarity[J].Physical Review Letters,2008(7):70401.
[2]Cozzini M,Stringari S.Fermi Gases in Slowly Rotating Traps:Superfluid vs Collisional Hydrodynamics[J].Physical Review Letters,2003(7):70401.
[3]Zwierlein M,Abo-Shaeer J,Schirotzek A,et al.Vortices and superfluidity in a strongly interacting Fermi gas[J].Nature,2005(7045):1047-1051.
[4]Yeong,E,Kim,Zubarev A L.Time-dependent density-functional theory for trapped strongly interacting fermionic atoms[J].Physical Review A,2004(3):33612.
[5]Zhang A X,Xue J K.Sound waves and dynamics of superfluid Fermi gases in optical lattices[J].Physical Review A,2009(4):3383-3387.
