厚壁管道轴向裂纹对C-SH0模态反射特性的影响
2021-04-21赵华民郑明方
赵华民, 郑明方
(1.山西农业大学 工学院,晋中 030801;2.东莞理工大学 环境与土木工程学院,东莞 523808)
厚壁管道是电力工业主蒸汽管道和再热蒸汽段中广泛使用的高温高压部件,其安全运行对整个电厂的安全有重要意义。为了预测缺陷的严重程度,需要准确估计电厂管道和压力容器中的缺陷尺寸[1]。然而,受检测范围、高辐射剂量等的限制,传统的无损检测技术很难检测所有管道中的缺陷[2]。超声导波可用于在固定位置和较宽的检测范围内对长管道进行检测,因此被广泛应用于板材[3]、管道[4]、铁轨[5]等工件的缺陷检测中。超声导波在不同的波导介质中呈现出不同的传播模式。管道中的超声导波可分为纵向、扭转、弯曲和周向等4种类型[6]。
为了分析缺陷尺寸与导波反射回波的关系,广大学者研究了裂纹、开槽[7-10]和其他类型缺陷之间的相互作用。MA等[11]对不同几何形状管道凹痕与导波反射特性进行了研究。ZHANG等[12]采用有限元方法研究了空心圆柱上圆孔和不同角度的裂纹缺陷的弯曲模态的反射特性。
周向导波又可分为周向兰姆波(C-Lamb)和周向剪切水平(C-SH)波[13]。ROSE等[14]研究了各向同性空心圆柱中水平剪切SH波的传播特性,导出了频散方程以及沿壁厚方向的位移场和应力场公式。LIU等[15]通过仿真研究了基于导波周向扫描和相位特性的管道缺陷定位方法。张小明等[16]研究了压电圆柱曲面板中的周向导波的复频散特性。ZHANG等[17]研究了管道腐蚀和裂纹缺陷的周向导波检测系统。
以上对周向导波的研究主要集中在其传播特性上,而对周向导波与缺陷的相互作用,特别是定量相互作用的研究较少。笔者分析了缺陷深度、缺陷长度和激励信号参数对周向导波反射系数的影响。研究了反射信号随裂纹长度、深度和入射信号频率变化的关系。为厚壁管道轴向缺陷的快速定量与识别提供理论依据。
1 周向导波理论
1.1 厚壁管中周向导波的频散特性
为了研究导波的传播特性,需要确定管道的频散曲线。利用MATLAB软件计算了周向导波在厚壁管道上的频散曲线。管道外径为141.3 mm,壁厚为12.5 mm,密度为7.9 g·cm-3,横波速度为3.26 mm·ms-1,纵波速度为5.96 mm·ms-1,泊松比为0.3。频厚积为06.5 MHz·mm的管道周向导波频散曲线如图1所示。
1.2 模态选择与波结构分析

图1 频厚积为06.5 MHz·mm的管道周向导波频散曲线
合适的模态和频率选择对于周向导波缺陷检测非常重要。为了降低检测过程中多模态处理的难度,选择低频范围内的模态。由图1可知,在频厚积为01.65 MHz·mm时,只有C-SH0、 C-A0和C-S0模态无频散,并且C-SH0模态的频散小于C-A0和C-S0模态的。
波结构为质点位移在管道壁厚上的分布,对导波波结构的分析有助于选择合适的模态和优化检测参数,如激励频率,以提高导波对整个厚壁管道的检测能力。
式(1)为周向SH波波动方程中的轴向位移uz的通解,由式(1)可以计算出沿管道壁厚方向不同频率下的周向C-SH0振型的归一化位移分布。
uz=[AJp(ktr)+BYp(ktr)]·exp[i(pθ-ωt)]
(1)
式中:kt=w/ct,ct为横波速度;p和ω分别为角波数和角频率;Jp和Yp分别为给定角波数下的一阶和二阶贝塞尔函数;常数A和B由质点位移决定。
不同频率下C-SH0模态波结构如图2所示,在频率为60,80,100 kHz时,周向C-SH0模态以轴向位移为主。因此,可以用正入射横波探头沿管道周向激励C-SH0模态,从而将C-SH0模态应用于管道轴向裂纹的检测中。

图2 不同频率下C-SH0模态波结构

图3 外径为141.3 mm,壁厚为12.5 mm厚壁管的有限元模型
2 仿真模型的建立
利用ABAQUS软件对管道中周向导波与轴向缺陷的相互作用进行数值仿真。外径为141.3 mm,壁厚为12.5 mm厚壁管的有限元模型如图3所示。模型尺寸和材料的设置与图1中用于计算频散曲线的尺寸和材料相同。缺陷轴向长度和周向宽度分别用l和w表示,模拟缺陷沿管道中线布置。缺陷外壁开口宽度为3.3 mm,对应的内壁开口宽度为2.7 mm。为了减少计算时间和保证仿真精度,采用六面体单元,类型选择C3D8。为了保证动态解的良好收敛性,每个波长需要1020个网格[18],所以网格尺寸设置为1.25 mm。在管道外表面的中心点加载5周期汉宁窗调制脉冲信号,激励信号中心频率为55 kHz110 kHz。激励信号采用多周期脉冲,有利于获得单一模态的导波信号,但过多的周期会导致信号时域过宽和波包重叠,因此采用5周期汉宁窗调制信号点激励产生周向导波。激励源和缺陷中心都位于管道的轴线上,其中心的夹角为90°。另外,在激励源的两侧各设置5个反射信号接收点。基于试验模拟,点的位置应具有最强的反射波场进行,同时考虑到传感器直径一般不大于20 mm,所以每2个接收点的距离设为2 mm。
仿真中激励周向导波时,不仅产生沿管道周向传播的导波,而且产生沿管道轴向传播的导波,所以管道长度应至少为900 mm,以将沿管道轴向传播的信号与沿管道周向传播的信号分开。因此,设置管道长度为1 000 mm。
图4为图3中沿表面A的截面。图4中,d为裂纹深度,ta为管壁厚度。管道实际使用中,裂纹可能从外表面向内延伸,也可能沿管径向膨胀。因此,需要建立内外表面轴向裂纹模型以研究不同模态导波与裂纹的相互作用。

图4 管壁内外缺陷示意
3 仿真结果与讨论
3.1 模态确认
为了证明点激励可以得到单一的C-SH0模式,在进行时域分析之前,首先对无缺陷管道进行了周向波导模拟。周向导波的传播云图和时域波形如图5所示。入射波的中心频率为80 kHz。
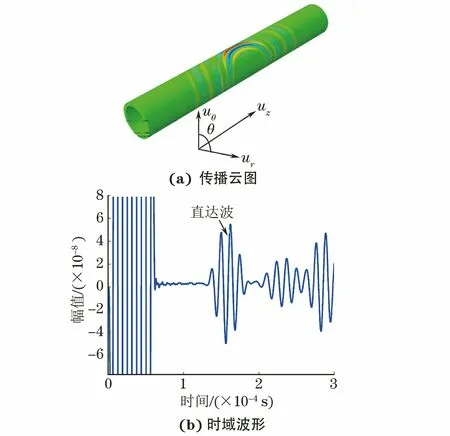
图5 周向导波的传播云图和时域波形
通过计算得到的时域波中直达波波速为3 219 m·s-1,与理论计算C-SH0模态群速度3 241 m·s-1一致。除了验证波速,还绘制了C-SH0模态在无缺陷管道中传播的位移波结构图,并与由频散方程得到的波结构图进行了比较。提取沿管壁径向分布的21个等间距点上的信号,将直达波的振幅归一化并取最大值,根据点的径向位置绘制位移波结构图。仿真结果与频散方程计算结果基本一致,证明直达波为C-SH0模态。
3.2 反射系数
图6为80 kHz时的周向导波时域信号包络图。由图6可知,l=60 mm时,d/ta为50%时的信号为C-SH0模态,轴向裂纹反射波包位于入射波信号和直达波信号之间,且清晰可见。

图6 80 kHz时的周向导波时域信号包络图
定义反射系数为特定模态下主反射信号的位移幅值与沿无缺陷管道周向传播直达波位移幅值之比。因此,反射系数R如式(2)所示。
R=Ar/Ad
(2)
式中:Ar为缺陷反射波的最大幅值;Ad为无缺陷管道中的直达波的最大幅值。
因此,时域反射系数由信号包络的最大值来计算。
3.3 中心频率对R的影响
图7所示为C-SH0的反射系数R在d/ta为25%,50%,75%,100%时与激励频率的变化关系。l=60 mm,在d/ta为25%,50%,75%时,反射系数与激励频率呈近似线性关系。d/ta为100%时的反射系数比d/ta为75%时的低。这是由非穿透裂纹近端反射与远端反射之间的干涉所产生的。这种现象会影响最终反射信号的时域振幅。当频率大于90 kHz时,C-SH0模态的反射系数曲线快速上升,这是因为在不同频率和模态下,直达波的衰减不同。
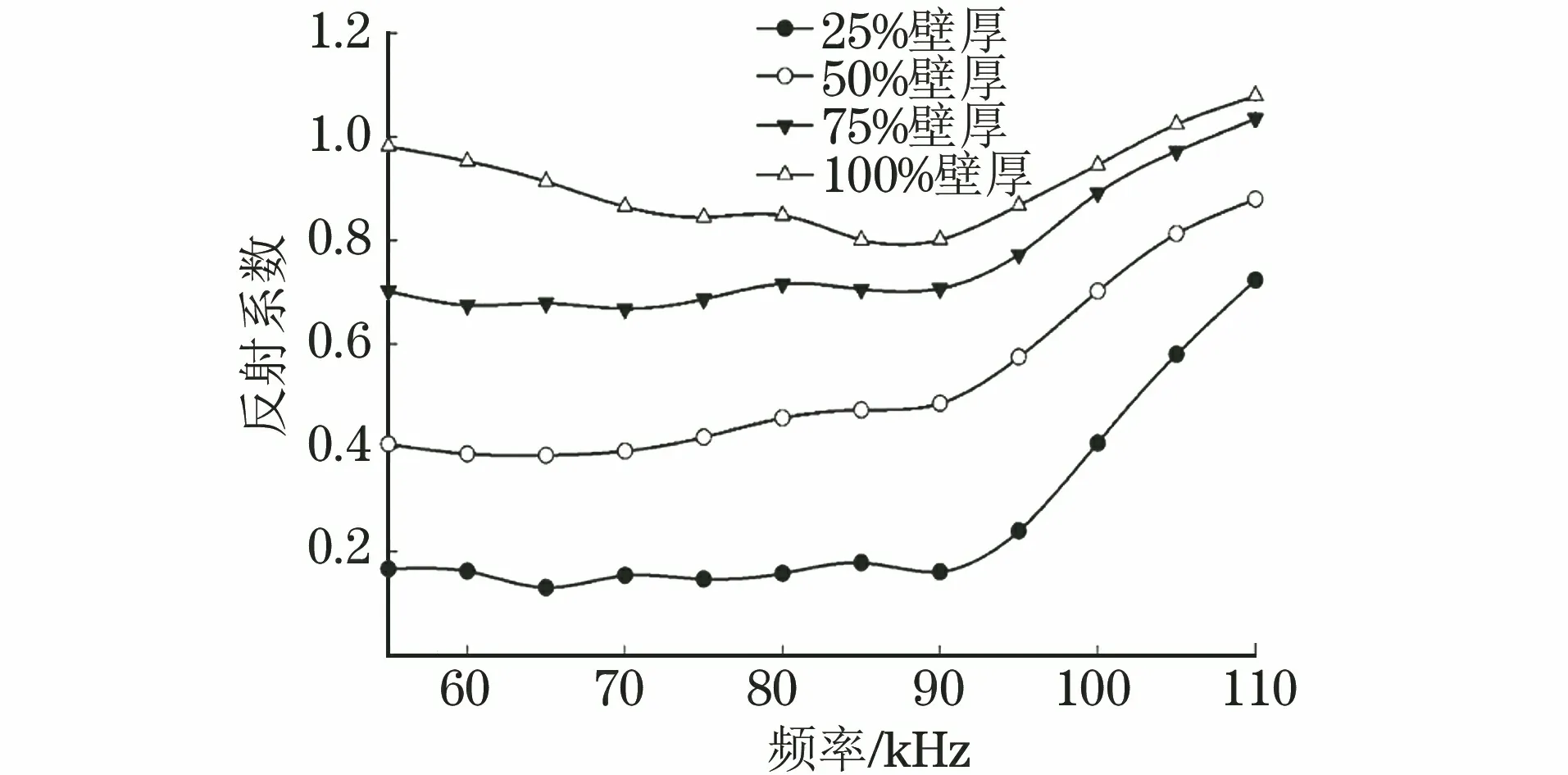
图7 反射系数与激励频率的关系曲线
当频率大于100 kHz时,会出现严重的频散现象。这对反射系数的测量和计算有很大的干扰。因此,在选择激励信号的中心频率时,应考虑频率的上限。周向C-SH0模态的检测频率为55 kHz110 kHz。

图8 在固定激励频率和不同的d/ta时反射系数与裂纹长度的关系曲线
3.4 裂纹长度对R的影响
图8为在固定的激励频率和不同的d/ta时,C-SH0模态的反射系数与裂纹长度的关系。文中相对裂纹长度定义为裂纹长度l与激发波长λ的比值。由图8可知,对于不同深度的裂纹,R首先随裂纹长度的增加而增大,然后上下波动。关系曲线的平稳程度与裂纹的深度有关,随着裂纹深度的增加,曲线的上下波动更加明显。当l/λ=2时,R达到最大值。随着裂纹长度的增加,关系曲线上下波动,这是由沿裂纹表面传播的波的干涉引起的。当l/λ<2时,衍射效应显著,衍射信号与反射信号一起到达管道的接收信号位置,从而提高了接收信号的振幅;当l/λ>2时,接收信号的相位差很大,引起叠加信号的波动。与非穿透裂纹相比,对穿透裂纹,由于裂纹两端波的干扰,其趋势呈现出较大的波动。
3.5 裂纹深度对R的影响
图9为激励频率为80 kHz时不同裂纹深度对R的影响曲线。相对深度定义为径向深度d与壁厚ta之比。仿真中设置裂纹径向深度分别为1.25,2.5,3.75,…,12.5 mm(以1.25 mm递增),分别相当于ta的10%,20%,30%,…,100%(以10%递增)。分别在l为40,60 mm时研究不同d/ta对R的影响。裂纹宽度与之前的设置相同。

图9 激励频率为80 kHz时不同裂纹深度对R的影响曲线
对于相同长度的轴向裂纹,当C-SH0模态在管壁的外表面或内表面传播时,R具有相同的变化趋势。原因是在低频范围内,C-SH0模态的波结构基本相同,外表面和内表面质点振动的轴向位移也相同。
3.6 不同深度和频厚积对R的影响

图10 不同频厚积下R与裂纹深度的关系
在不同频厚积下,反射系数随裂纹深度的变化趋势如图10所示。保持管径不变(141.3 mm),壁厚分别为12.5,15,16 mm。激励频率分别为65 kHz和80 kHz,l=60 mm,d分别取4%,8%,12%,…,100%壁厚。在5种不同的频厚积下,R具有很高的相似性,随着裂纹深度的增加而线性增加。频厚积等于1 000 kHz·mm时的R大于800 kHz·mm时的。当入射波激励频率为65 kHz时,反射系数随壁厚的增加而增大。结果表明,频厚积影响C-SH0模态的频散,该结果也适用于其他壁厚。
3.7 不同深度和轴向长度对R的影响
当周向C-SH0波在含轴向裂纹的管道中传播时,R与裂纹尺寸的关系可以定量研究,即在固定轴向长度下R与裂纹深度的关系,以及在固定深度下R与裂纹轴向长度的关系。设置了周向宽度为3.0 mm的轴向缺陷来模拟轴向裂纹,并改变轴向裂纹的深度和长度,深度变化范围为4%,8%,12%,…,100%壁厚,轴向长度由2,4,6,8 mm逐渐变化至60 mm,按照前文所述进行激励和分析。因此,仿真共包括750个三维管道模型,激励模态为C-SH0。为了达到研究目的,使用ABAQUS-Python进行参数化编程,研究了R与裂纹尺寸之间的关系(见图11)。
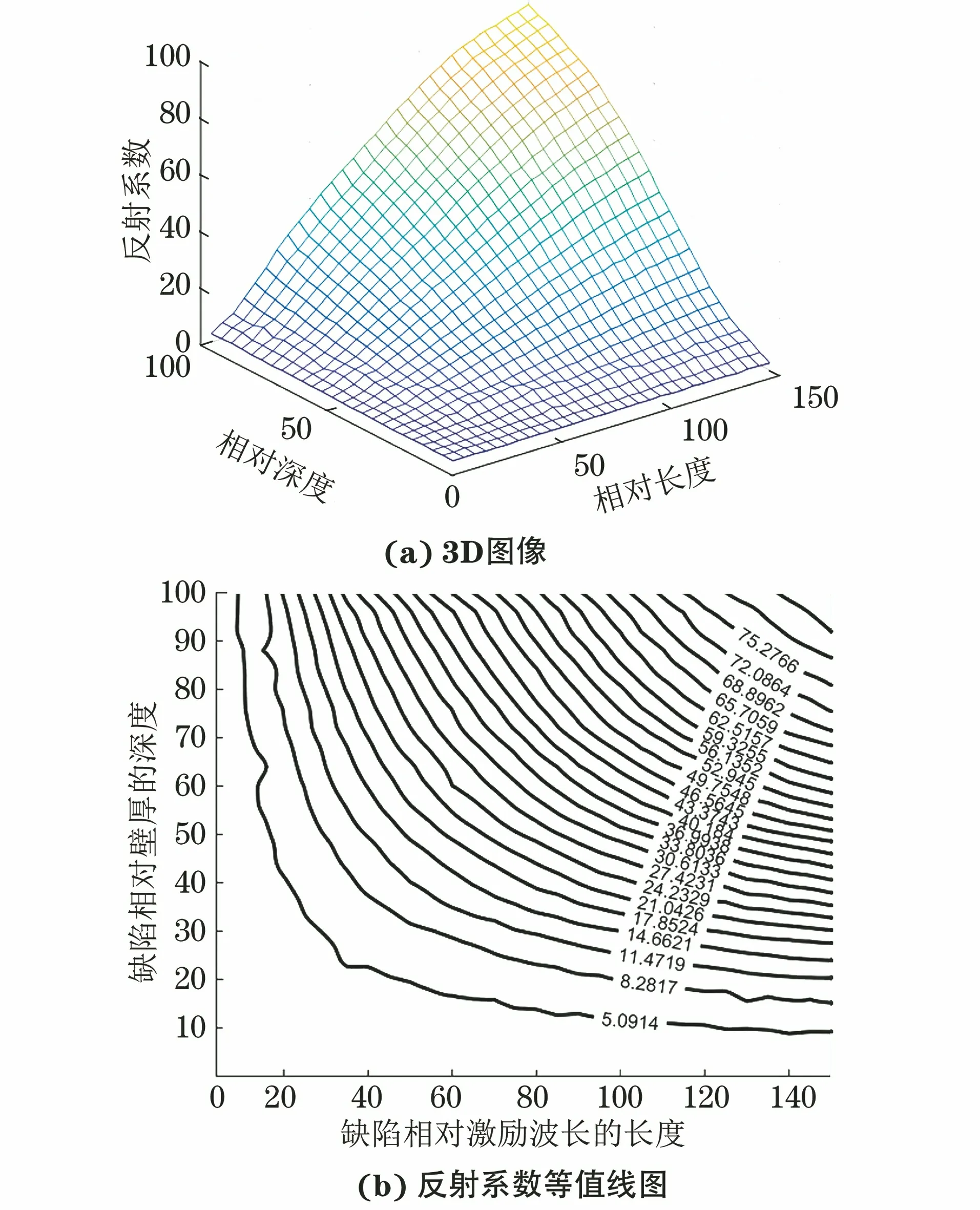
图11 C-SH0模态R与缺陷尺寸关系的三维图形和等值线图
利用R与相对缺陷尺寸(长度和深度)之间的两个定量关系,可以获得C-SH0模态的R的3D图像[见图11(a)]。三维图形显示了直径为141.3 mm的钢管中,当周向C-SH0模态在80 kHz频率下传播时,轴向范围和径向深度不同的轴向缺陷对R的影响的定量评估结果。在特定的缺陷深度下,R随缺陷长度的增加单调增加;在特定轴向长度下,R随缺陷深度的增加而增加。图11(b)中的黑白等高线图表明,不同深度和长度的轴向裂纹缺陷的R可能相同。当同一等高线上任意一点的垂线分别与纵横轴线相交时,用同一反射系数对应的交点的纵横坐标可以确定不同的轴向缺陷的深度和长度。结果表明,利用图11(b)所示的等值线图,可以很容易地从反射系数中得出缺陷的相对尺寸。
4 结语
研究了厚壁管中C-SH0模态与轴向裂纹的相互作用。结果对周向导波在电厂管道缺陷检测中的应用具有重要意义。采用三维有限元方法分析了周向导波沿管道周向的传播。根据频散曲线和波结构理论,总结了激励频率对C-SH0模态反射回波的影响规律。根据得到的规律,选择了最佳周向导波激励频率,对管道内外表面缺陷进行了检测。结果表明,在一定频率下,C-SH0模态的R随裂纹长度的增加而增大,并最终达到振荡状态。对于一定长度的轴向裂纹, C-SH0模态在内外壁传播时,R具有相同的变化趋势。最后利用基于ABAQUS-Python的自动建模与仿真程序包,得到了C-SH0模态R与缺陷尺寸关系的三维图形和等值线图。由反射系数等值线图可以得到缺陷的相对大小。为进一步的相关试验和实际应用提供了理论指导。
