基于灰狼算法的车辆配送物流路径优化研究
2021-04-21吴慧君
吴慧君
(福建船政交通职业学院,福建 福州 350007)
带容量约束的车辆路径问题(capacitated vehicle routing problem,CVRP)的主要特征是车辆有最大容量限制、各客户需求点有货物配送需求,该问题是一种典型的非确定性多项式(non-deterministic polynomial,NP)难题组合优化问题[1]。传统算法很难求解CVRP问题,近年来很多研究人员将群智能算法应用于CVRP问题求解。文献[2]将混合变邻域生物共栖搜索算法应用于CVRP问题求解。文献[3]将多种群人工蜂群算法用来求解带重新路由策略的CVRP问题。文献[4]提出了一种基于改进的粒子群优化算法的车辆路径优化方法。
灰狼优化算法(grey wolf optimization algorithm,GWO)是模仿灰狼等级划分和灰狼捕食行为而提出的群智能搜索算法[5]。该算法具有控制参数少、收敛速度快和计算简单等优点,已在机器学习、函数寻优、数据挖掘、电力调度、控制器设计调优等方面得到广泛应用[6-7]。目前应用灰狼优化算法求解CVRP的文献较少,因此本文提出一种基于GWO的农产品物流配送车辆路径优化方法。研究结果表明,与PSO和GA相比,在行驶里程和平均行驶成本方面,GWO的成本最低且行驶里程最少。
1 GWO算法
GWO算法中,灰狼个体分为α、β、δ和ω,其中,α负责狼群的决策与管理;β和δ为适应度次于α的灰狼个体;ω为其他灰狼个体。GWO算法主要包括包围、捕猎和攻击三种行为。
1.1 包围
在整个算法过程中,首先灰狼包围猎物,数学模型如公式(1)和公式(2)所示:
(1)
(2)
1.2 捕猎
包围猎物之后,狼群将捕猎猎物。假定α、β、δ分别为全局最优解、全局第二解以及全局第三解,对α、β、δ重新定位:

(3)
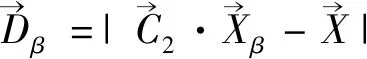
(4)
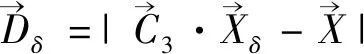
(5)
(6)
(7)
(8)
(9)
1.3 攻击
狼群捕食的最后阶段就是攻击捕获猎物,攻击过程主要通过调节参数a实现。当|A|≤1时,狼群将接近猎物(X*,Y*)集中攻击猎物;当|A|>1时,狼群将远离猎物。
2 农产品车辆配送物流路径优化
2.1 问题描述
农产品物流车辆路径优化可表述为[8-9]:假设农产品中心仓库,该中心仓库配备有K辆物流运输车,车辆载重容量为qk(k=1,2,3,…,K),配送需求点有L个,第i个需求点的需求量为gi(max(gi)≤max(qi)),完成需求点任务i农产品装载或卸货的时间为Ti,其中任务i必须在时间段[ETi,LTi]内完成。ETi、LTi分别为任务i的最早开始时间和最迟开始时间。若农产品配送车辆早于ETi到达需求点,则配送车辆等待;否则,任务将被延迟。农产品物流车辆配送示意图如图1所示。

图1 农产品物流车辆配送示意图
2.2 数学模型
根据问题描述将农产品需求点编号为1,2,3,…,L,物流配送中心仓库编号为0,任务和中心仓库被编号为i=(0,1,2,3,…L),那么决策变量为[10]:
xijk={1 车k从点i行驶到点j
0else
(10)
yki={1 发货点i任务由k车完成
0else
(11)
综合所述,农产品车辆物流配送路径数学规划模型为:
(12)
(13)
(14)

(15)
式中,cij为需求点i到需求点j的运输成本;si为配送车辆到达需求点i的时间;PE、PL分别为农产品物流配送车辆提前达到或者滞后到达需求点i的单位时间内的等待成本和惩罚成本。该数学模型中每个需求点均有车辆配送,且每个需求点只能由一辆农产品物流配送车辆配送;与此同时,同一配送路径上的需求点的需求量之和应小于等于农产品物流配送车辆的最大载重。
2.3 算法流程
为实现农产品物流配送车辆路径的最优规划,解决该问题的关键是构造合适的灰狼α的表达方式。在参考文献[11-12]的基础上,构造一个2L维空间对应L个需求点任务的农产品物流配送车辆路径规划问题,保证需求点任务为2维。若需求点任务为7,配送车辆为3,需求点任务编号为[1 2 3 4 5 6 7]。此时灰狼α位置向量X如图2所示,其中灰狼α位置对应物流配送车辆的编号和行驶路径。

图2 车辆和路径编号
则该灰狼α位置对应的农产品物流车辆配送路径为:1)车辆1:0→1→0;2)车辆2:0→4→5→3→2→0;3)车辆3:0→7→6→0。
基于GWO的车辆配送物流路径优化算法步骤具体描述如下:
Step1:设定GWO算法参数:种群规模N、最大迭代次数Maxgen;
Step2:初始化灰狼位置;
Step3:按式(15)计算每只灰狼的适应度,将适应度排在前三的灰狼个体位置分别记作Xα、Xβ和Xδ;
Step4:按式(3)分别计算各ω狼与α、β、δ狼之间的近似距离,并按式(4)和式(5)更新α、β、δ狼的位置和猎物的位置;
Step5:更新参数a、A和C;
Step6:判断算法终止条件:若达到最大迭代次数Maxgen,则输出最佳灰狼α的位置作为农产品车辆物流配送最佳路径。
3 仿真试验与结果分析
为了验证GWO进行农产品物流配送车辆路径优化的有效性和可靠性,选择参考文献[13]中的实例为研究对象,用户需求和中心仓库与各需求点的坐标位置如表1和表2所示。
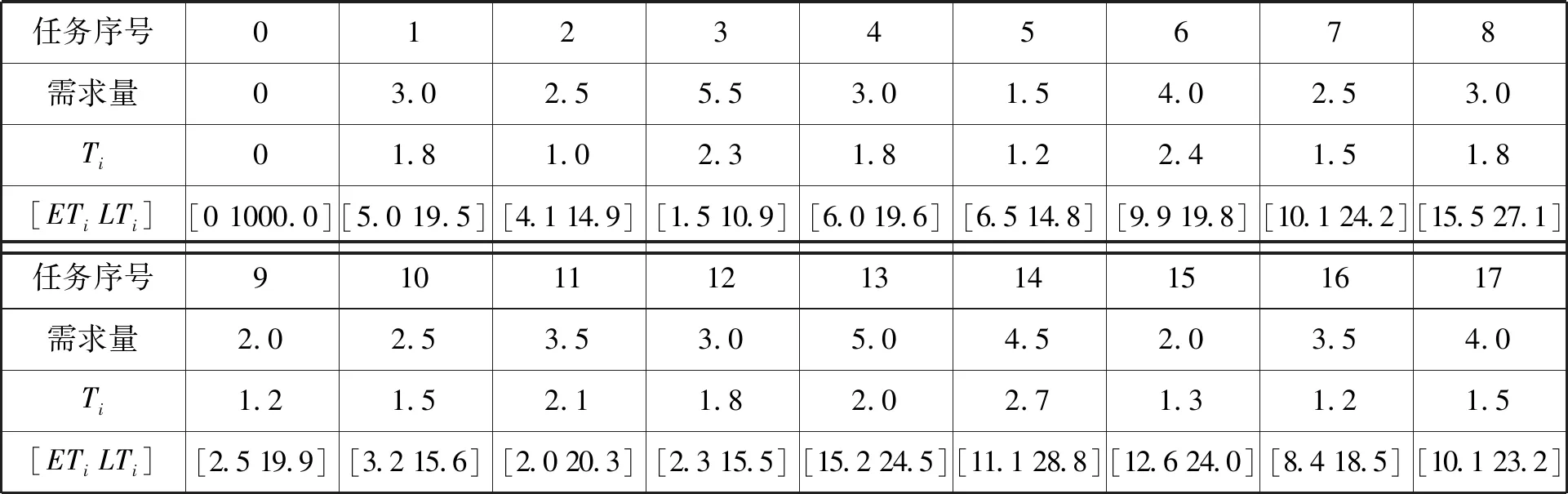
表1 配送中心和用户需求任务

表2 配送中心和需求点坐标
将GWO和PSO、GA进行对比,不同算法参数设置如下:1)GWO参数:种群规模N=50、最大迭代次数Maxgen=500;2)粒子群算法(particle swarm optimization algorithm,PSO)参数:种群规模N=50、最大迭代次数Maxgen=500、学习因子c1=c2=2、惯性权重w=0.2;3)遗传算法(genetic algorithm,GA)参数:种群大小N=50,交叉概率Pc=0.7和变异概率Pm=0.1和最大迭代次数Maxgen=500,对比结果如图3~图8所示。

图3 GWO配送路径

图4 GWO寻优收敛图
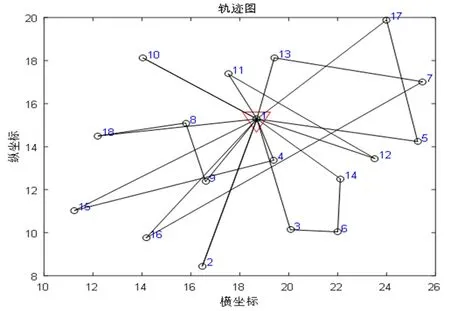
图5 PSO配送路径
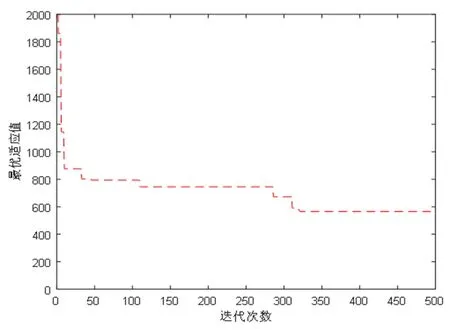
图6 PSO寻优收敛图
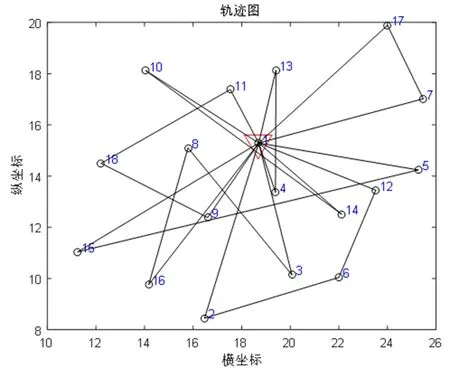
图7 GA配送路径
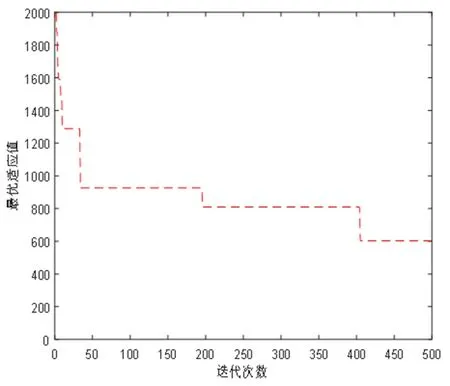
图8 GA寻优收敛图
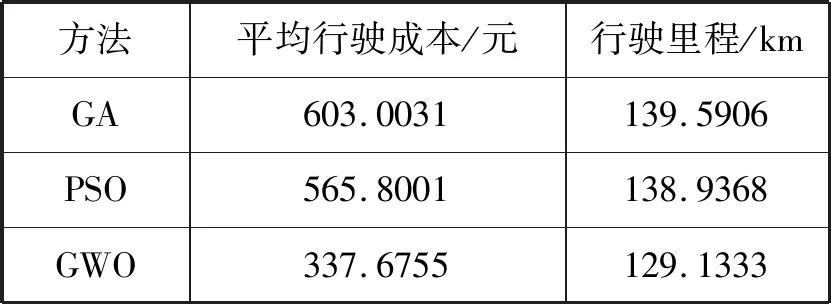
表3 GWO、PSO和GA对比结果
由表3和图5~图8可知,与PSO和GA相比,在行驶里程和平均行驶成本方面,GWO的成本最低且行驶里程最少,从而验证了基于GWO进行农产品物流车辆配送路径优化的有效性和可靠性。
4 结论
本文运用灰狼优化算法求解农产品物流配送路径规划问题。研究结果表明,与PSO和GA相比,在搜索时间和平均行驶成本方面,GWO的配送成本最低且行驶里程最少,为农产品物流配送车辆路径优化提供了新的方法。
