基于三焦张量的视觉辅助惯性定位方法

孙 伟，刘思琪

基于三焦张量的视觉辅助惯性定位方法

孙 伟，刘思琪

（辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000）

针对单一惯导解算误差易随时间累积的问题，提出一种视觉辅助惯性定位方法：利用三张影像构建三焦张量模型，并求解相机位姿信息作为量测模型；然后通过随机抽样一致算法，对连续影像中获得的特征点进行筛选，剔除误匹配及运动物体上的特征点后，通过无损变换使其满足非线性特征；最后采用多状态约束卡尔曼滤波滑动窗口，对两个系统输出信息进行滤波修正。实验结果表明，该方法能有效地解决单一惯导误差漂移问题，并且其精度和均方根误差均优于传统的多状态约束卡尔曼滤波的视觉辅助定位方法。

视觉导航；惯性导航；三焦张量；多状态约束；随机抽样一致算法

0 引言

惯导系统定位误差随时间累积，无法长时间独立开展定位工作，视觉匹配导航方法能够限制惯导系统解算误差累积并实现对位置误差的修正[1-3]。众多学者围绕相关技术开展适应性研究并取得一定成果。其中，文献[4]提出扩展卡尔曼滤波（extended Kalman filter, EKF）测量模型，实现视觉辅助惯导的多传感器融合，但在线性化过程中，只保留的一阶或二阶项，在高度非线性环境下，会产生误差累积；文献[5]提出对极几何来完成动态视觉估计，但其获取的连续两张影像特征点的位姿会出现奇异；文献[6]提出基于三焦点张量求解摄像机运动参数并实现了车辆运动参数的估计，但无法剔除视觉定位中误匹配的特征点。针对上述问题，本文提出一种基于三焦张量的视觉辅助惯性定位方案，即采用多状态约束卡尔曼滤波（multi-state constraint Kalman filter, MSCKF）滑动窗口，对视觉导航和惯性导航系统输出的信息进行融合滤波修正，以此提高系统定位精度。

1 三焦张量建模

与对极几何相似[7]，三焦张量建模是指在连续三张影像中构造几何关系，如图1所示。连续影像的选择，需要满足在三张影像中，包含一定数量相同的特征点，确定三焦张量后，即可从中提取相机在三个位置的姿态矩阵，根据三张影像中的相同特征点位置变化获得相机的位姿信息。

图1 三焦张量模型

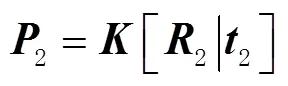
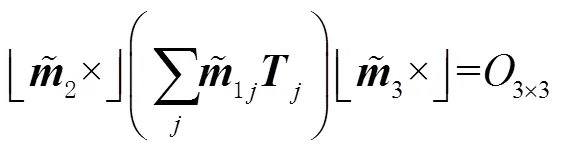
三焦张量不仅能满足空间中某一点在三张影像中投影得到相机的位姿信息，还可以通过空间中某一线段获取相应位姿信息。同理推导出三焦张量的“点-点-线”关系式为

2 基于随机抽样一致算法的连续影像特征点选取

通过三焦张量模型得到的特征点中存在误匹配点，将不同影像中相同特征点进行有效匹配是视觉导航的核心。本文采用随机抽样一致算法（random sample consensus, RANSAC）[8-10]来剔除匹配错误或移动物体上的特征点并留下“局内点”。首先，利用RANSAC来选取“局内点”，其表达式为

从特征点组中随机挑选一组数据进行量测更新，计算出符合该组特征点关系中的所有“局内点”。最后回到特征点中找到存有最多“局内点”的特征点组来进行量测更新[11]。

3 基于三焦张量的滤波融合算法

使用视觉辅助惯导系统进行定位时，需要利用相机得到的特征点的位姿信息、以及连续影像的相对位姿信息作为滤波更新中的量测信息，两个系统相互约束可提高定位精度，与常规视觉导航不同，量测信息是由三焦张量模型获得的，用来辅助修正惯导信息[12]。

3.1 状态方程

滤波器状态可划分为标称状态和误差状态，根据提出的方法可知，需要三幅影像进行滤波更新，那么相应的惯导系统也要获取三个时刻位姿信息，标称状态是由惯导系统的测量单元、通过运动获得输出信息构成的[13-14]。其标称状态可以表示为：

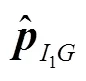
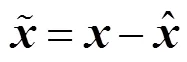
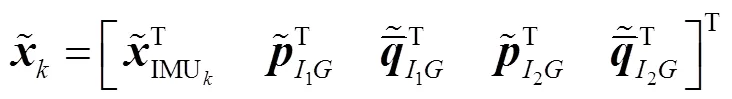
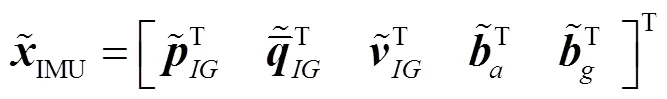
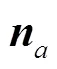
预测过程中的前一时刻位姿，在滤波器中不随时间变化，不参与状态方程更新，运动模型可定义为：

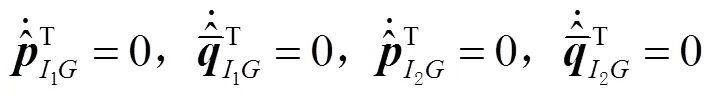
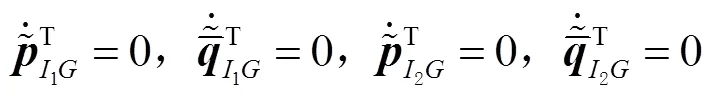
3.2 量测方程

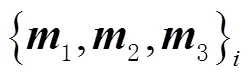
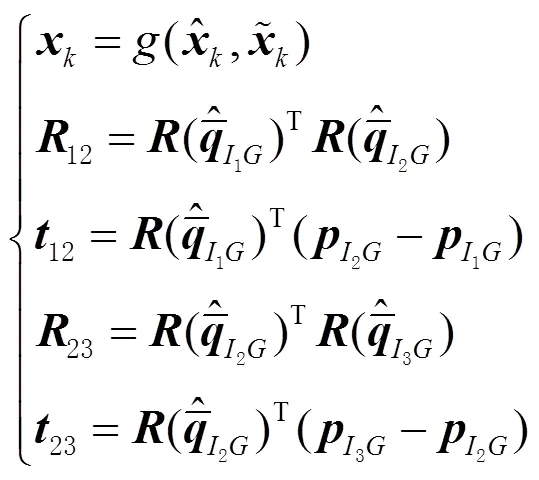
3.3 基于三焦张量的MSCKF方程

根据式（9）描述的惯导系统输出位姿信息，建立连续时间增广误差的状态方程为

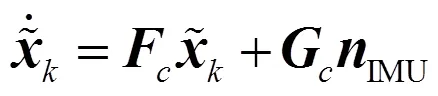
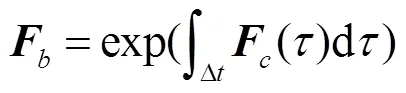
误差状态协方差矩阵预测更新为

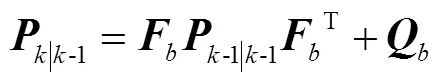
为提高量测模型非线性测量精度，采用无损变换（unscented transform, UT），选取西格马（Sigma）点[15]后，基于MSCKF滤波器更新。选取Sigma点的计算方法为

将得到的Sigma点带入量测模型，计算出测量值为

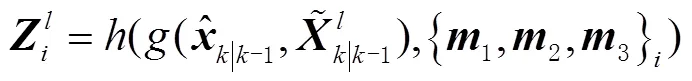
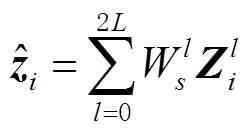
其中，

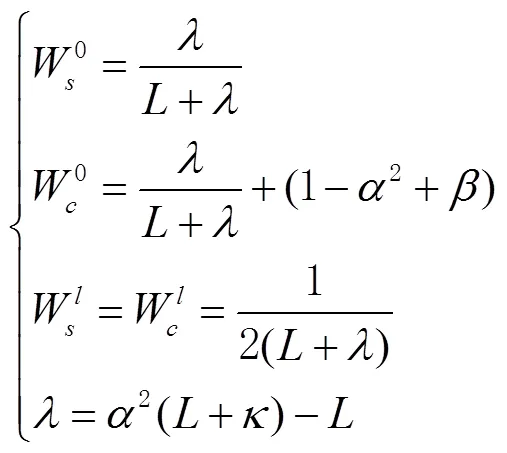
状态值和测量值之间的协方差矩阵为

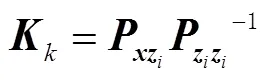
根据卡尔曼滤波方程，状态值与状态协方差矩阵做量测更新，即：

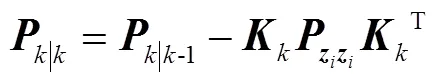
4 仿真结果及分析

1）RANSAC算法仿真结果及分析。如图2所示，在图2（a）中，传统特征点匹配方法共提取32对特征点，其中存在较多的误匹配点；在图2（b）中，RANSAC算法剔除了这些误匹配点。RANSAC算法具有较高的误匹配点剔除能力，获得最大“局内点”集合并求得最佳模型，依赖RANSAC算法筛掉误匹配特征点，可提高视觉导航精度。

图2 RANSAC算法优化前后的特征点匹配比较

2）基于三焦张量的视觉辅助惯性定位方法的仿真结果及分析。采用由德国卡尔斯鲁厄理工学院和丰田美国技术研究院联合创办的公开数据集，获取不同路径下记录的传感器同步数据，将全球定位系统（global positioning system, GPS）及惯性测量系统（inertial measurement unit, IMU）组合定位结果作及惯性组合作为参考基准，通过轨迹图、均方根误差（root mean square error, RMSE）图以及RMSE，从姿态和位置两个方面，对三种定位方法进行对比，以验证基于三焦张量的方法用于定位的可行性，比较结果如图3、图4所示。

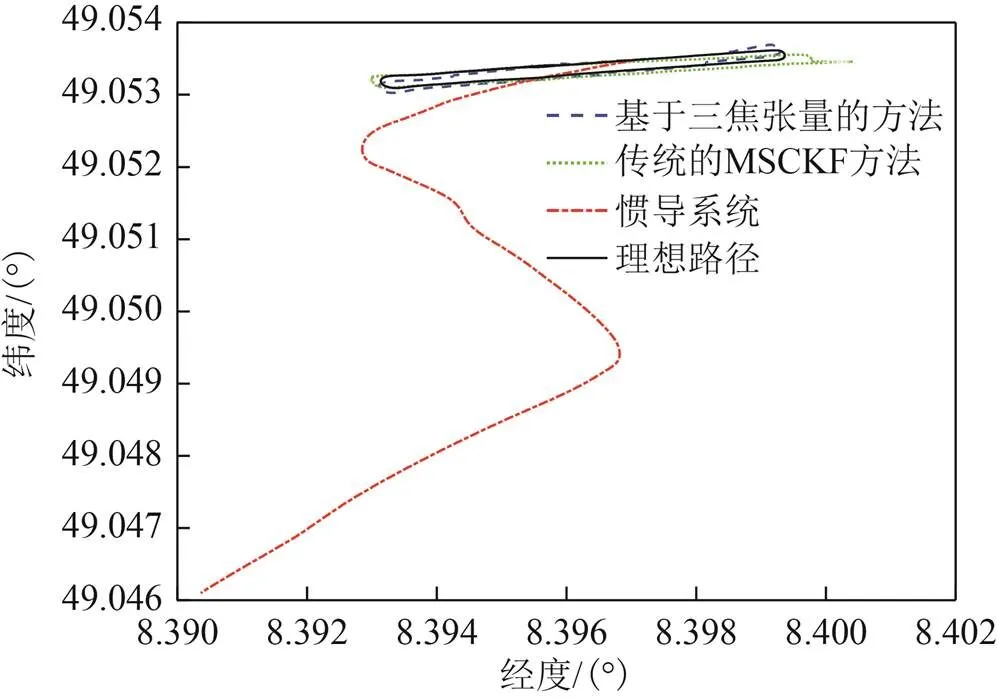
图3 移动轨迹比较

从图3中可以看出：惯导系统的定位结果随时间的增加，轨迹严重偏离理想路线并呈发散状态；而在另外两种方法中，基于三焦张量的方法相比传统的MSCKF方法更接近理想路线。

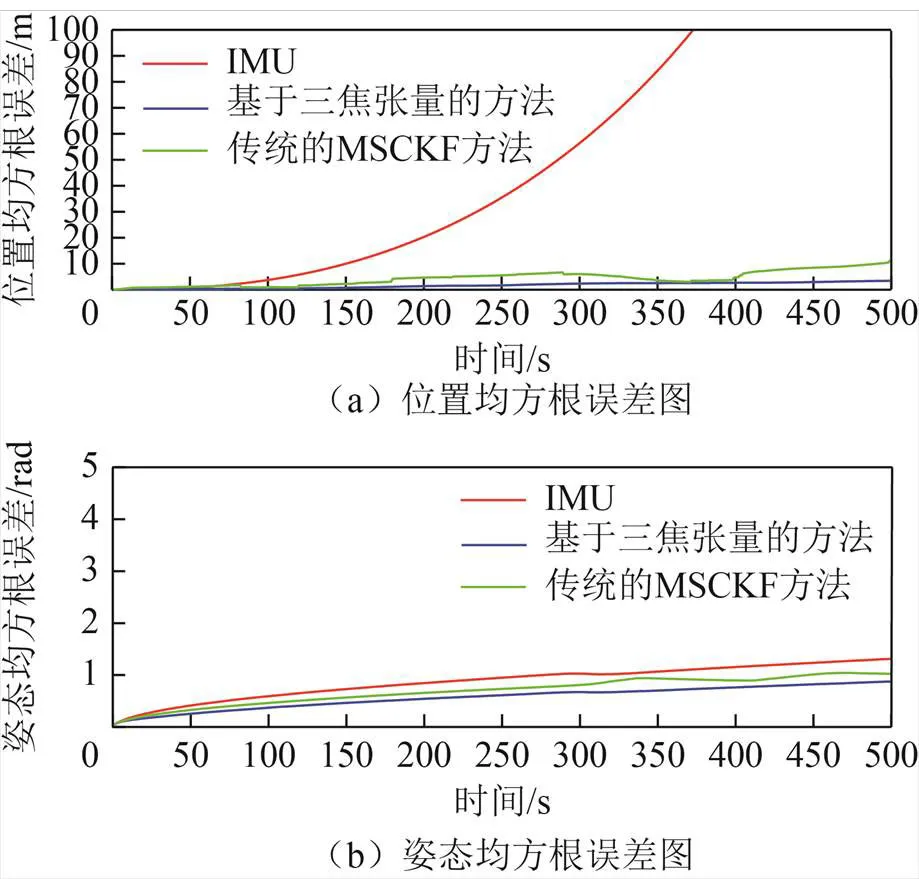
图4 均方根误差比较

从图4可以看出：随时间的增加，惯导系统的测量值与真值偏差越来越大，且传统的MSCKF方算法相比于基于三焦张量的方法具有更大的误差，因此，基于三焦张量的方法与传统的MSCKF方法相比，定位精度有一定的提高。三种定位方法的RMSE比较见表1。

从表1可以看出，惯导系统的位置均方根误差达到了420.15 m，其定位结果不具可用性。传统的MSCKF方法的位置RMSE为9.76 m，而基于三焦张量方法的位置RMSE只有传统MSCKF方法的一半。同时，基于三焦张量的方法的姿态RMSE与传统的MSCKF方法和惯导系统的姿态RMSE虽然相差不大，但其姿态RMSE是最小的。值得注意的是，惯导系统的姿态RMSE与另外两种方法的RMSE相差不大，这是因为惯导系统中的陀螺仪获得的角度信息只需要进行一次积分，所以相对于位置信息，惯导系统的姿态信息更加可靠。

表1 三种定位方法的位置和姿态RMSE比较

仿真结果验证了基于三焦张量的视觉辅助惯导系统的定位方法性能最好，其定位精度更高。

5 结束语

本文提出了基于三焦张量的视觉辅助惯性方法，只需利用三张影像构建三焦张量模型并求解相机位姿信息，作为量测模型用于量测更新，通过随机抽样一致算法，对连续影像中获得特征点进行筛选，剔除误匹配及运动物体上的特征点后，通过UT变换使其满足非线性特征。与惯导解算结果对比可看出，该方法均方根误差较低且定位精度更有优势。

[1]冯国虎, 吴文启, 曹聚亮, 等. 单目视觉里程计/惯性组合导航算法[J]. 中国惯性技术学报, 2011, 19(3): 302-306.

[2]ÖZASLAN T, LOIANNO G, KELLER J, et al. Autonomous navigation and mapping for inspection of penstocks and tunnels with MAVs[C]//The Institute of Electrical and Electronic Engineers (IEEE). Proceedings of Robotics and Automation Letters. United States: IEEE, 2017: 1740-1747[2020-06-24].

[3]HESCH J A, KOTTAS D G, BOWMAN S L, et al. Consistency analysis and improvement of vision-aided inertial navigation[C]//The Institute of Electrical and Electronic Engineers (IEEE). Proceedings of Transactions on Robotics. United States: IEEE, 2014: 158-176[2020-06-24].

[4]张红良, 郭鹏宇, 李壮, 等. 一种视觉辅助的惯性导航系统动基座初始对准方法[J]. 中国惯性技术学报, 2014, 22(4): 469-473.

[5]STEFANO S, RUGGERO F, PIETRO P. Motion estimation via dynamic vision[C]//The Institute of Electrical and Electronic Engineers (IEEE). Proceedings of Transactions on Automatic Control. Jinan: IEEE, 1996: 393-413[2020-06-24].

[6]KITT B, GEIGER A, LATEGAHN H. Visual odometry based on stereo image sequences with RANSAC-based outlier rejection scheme[C]//The Institute of Electrical and Electronic Engineers (IEEE). Proceedings of Intelligent Vehicles Symposium. San Diego: IEEE, 2010: 486-492[2020-06-24].

[7]ZACHARIAH D, JANSSON M. Camera-aided inertial navigation using epipolar points[C]//The Institute of Electrical and Electronic Engineers (IEEE). Proceedings of Position Location & Navigation Symposium. Indian Wells: IEEE, 2010: 303-309[2020-06-24].

[8]WROBEL P B. Multiple view geometry in computer vision[J]. Kybernetes, 2001, 30(9/10): 1333-1341.

[9]FANG Qiang, ZHANG Daibing, HU Tianjiang. Vision-aided localization and navigation based on trifocal tensor geometry[J]. International Journal of Micro Air Vehicles, 2017, 9(4): 306-317.

[10]INDELMAN V, GURFIL P, RIVLIN E, et al. Real-time vision-aided localization and navigation based on three-view geometry[C]//The Institute of Electrical and Electronic Engineers (IEEE). Proceedings of Transactions on Aerospace & Electronic Systems. United States: IEEE, 2012: 2239-2259[2020-06-24].

[11]CIVERA J, GRASA O G, DAVISON A J, et al. 1-point RANSAC for EKF-based structure from motion[C]//The Institute of Electrical and Electronic Engineers (IEEE). Proceedings of International Conference on Intelligent Robots and Systems. Saint Louis: IEEE, 2009: 3498-3504[2020-06-24].

[12]蔡迎波. 基于多状态约束的视觉/惯性组合导航算法研究[J]. 光学与光电技术, 2015, 13(6): 62-66.

[13]CLEMENT L E， PERETROUKHIN V， LAMBERT J, et al. The battle for filter supremacy: a comparative study of the multi-state constraint Kalman filter and the sliding window filter[C]//The Institute of Electrical and Electronic Engineers (IEEE). Proceedings of Conference on Computer & Robot Vision. Halifax: IEEE, 2015: 23-30[2020-07-24].

[14]LI Mingyang, MOURIKIS A I. Improving the accuracy of EKF-based visual-inertial odometry[C]//The Institute of Electrical and Electronic Engineers (IEEE). Proceedings of International Conference on Robotics & Automation. Saint Paul: IEEE, 2012: 828-835[2020-06-24].

[15]胡高歌, 高社生, 赵岩. 一种新的自适应UKF算法及其在组合导航中的应用[J]. 中国惯性技术学报, 2014, 22(3): 357-361.

Visual assisted inertial positioning method based on trifocal tensor

SUN Wei, LIU Siqi

（School of Geomatics, Liaoning Technical University, Fuxin, Liaoning 123000, China）

Aiming at the problem that it is easy to accumulate over time for the calculation error of single inertial navigation, the paper proposed a visual assisted inertial positioning method: a three focus tensor model based on three images was established, and the camera pose information was solved as the measurement model; then the feature points obtained from continuous images were screened by the random sampling consistent algorithm, and after the mismatching and feature points on moving objects were eliminated, the points were made to meet the nonlinear characteristics through unscented transformation; finally the sliding window of multi state constrained Kalman filter was used to filter and modify the output information of the two systems. Experimental result showed that the proposed method could effectively solve the error drift problem of single inertial navigation, and its accuracy and root mean square error would be both better than those of the traditional visual aided positioning method based on multi-state constrained Kalman filter.

visual navigation; inertial navigation; trifocal tensor; multi-state constraint; random sampling consistent algorithm

P228

A

2095-4999(2021)02-0006-06

孙伟，刘思琪.基于三焦张量的视觉辅助惯性定位方法[J]. 导航定位学报,2021, 9(2): 6-11.（SUN Wei, LIU Siqi.Visual assisted inertial positioning method based on trifocal tensor[J]. Journal of Navigation and Positioning,2021,9(2): 6-11.）

10.16547/j.cnki.10-1096.20210202.

2020-07-09

2019辽宁省“兴辽英才计划”青年拔尖人才项目（XLYC1907064）；2019年辽宁省自然基金资助项目（2019-MS-157）；辽宁省高等学校创新人才支持计划项目（LR2018005）；辽宁省教育厅高等学校基本科研项目（LJ2017FAL005），2018年度辽宁省“百千万人才工程”人选科技活动资助计划项目（辽百千万立项【2019】45号）。

孙伟（1984—），男，黑龙江鹤岗人，博士，教授，博士生导师，研究方向为多源信息融合导航、自适应导航。

刘思琪（1996—），女，辽宁鞍山人，硕士研究生，研究方向为视觉导航与惯性导航。