中国区域电离层建模及其精度分析

陈永贵

中国区域电离层建模及其精度分析

陈永贵

（河南测绘职业学院，郑州 451464）

借助中国大陆构造环境监测网络（CMONOC）基准站中，全球定位系统（GPS）的原始观测数据，基于球谐函数建立中国区域电离层模型，实验结果表明：解算得出的32颗GPS卫星差分码偏差（DCB）的偏差在0.4 ns内，PRN-1号卫星的DCB与欧洲定轨中心（CODE）公布的偏差在0.3 ns内，新建模型的垂直总电子含量（VTEC）值与CODE公布的VTEC值残差在[-22]内，对比分析了COMONOC测站数量对建模结果的影响，提高测站的数量可以提高建立模型的精度。

中国大陆构造环境监测网络；球谐函数；总电子含量；硬件延迟偏差

0 引言

自进入20世纪末以来，基于地基全球卫星导航系统（global navigation satellite system, GNSS）观测数据，高精度地反演电离层电子含量（total electron content, TEC）就成为学者研究电离层方向之一。电离层对卫星导航定位的影响十分显著，这些影响直接表现在地面测站接收机接收到的卫星发射的测距码和载波相位信号所产生的时间延迟[1]。当GNSS 信号穿越大气层时，由电离层带来的误差，在接近地面方向时，其延迟误差可超过50 m，在太阳活动剧烈时，这种误差甚至可达100 m以上，虽然目前所使用双频观测值进行导航定位时，能够消除电离层误差带来的影响，但是双频观测值会放大噪声，因此，单频接收机仍占据着市场的大部分分额。在GNSS定位中，对电离层延迟误差进行改正就显得十分重要[2-3]。

美国喷汽实验室学者首次提出用基于地基全球定位系统（global positioning system, GPS）原始观测数据，确定电离层总电子含量的基本方法，并验证了基于地基GPS数据反演电离层电子含量的可行性[4]。同时，电离层具有十分丰富的时空特性，表现出很强的局部及区域特性，在没有测站分布或测站分别稀疏的地区建立区域电离层模型，其结果精度较差。因此，研究适用于中国区域的电离层产品显得很有必要。20世纪90年代末，文献[5]利用GPS数据，基于多项式函数首次探讨了我国区域电离层格网模型的建立方法；文献[6]借助 GPS 双频伪距值，建立并研究了小区域范围的电离层模型，并对该模型进行了精度评估；文献[7]基于站际分区的方法，来提取格网点的垂直总电子含量（vertical total electron content, VTEC）信息，并利用球谐函数构建了全球范围的格网模型；文献[8]利用北斗卫星导航系统（BeiDou navigation satellite system, BDS）多模实测数据，建立了实时电离层模型并进行了精度评估；文献[9]根据 GPS及格洛纳斯卫星导航系统（global navigation satellite system, GLONASS）数据，采用球谐函数建立了全球电离层格网模型并分析了不同因素对全球电离层模型精度的影响；文献[10]对南极地区电离层特征进行了球冠谐分析，验证了南极地区的电离层时空特性。

目前国内大多数采用的电离层模型是欧洲定轨中心（Center for Orbit Determination in Europe, CODE）发布的全球电离层模型产品，CODE提供的全球电离层总电子含量（total electron content, TEC）数据，具有较好的时间连续性，但CODE的监测站密集分布在欧洲地区及美国、在中国境内很少，导致中国区域的全球电离层模型（global ionospheric maps, GIM）数据精度较低，不能准确地反映中国区域的电离层精细变化。因此，借助中国大陆构造环境监测网络（Crustal Movement Observation Network of China, CMONOC）中的GPS观测数据，建立中国区域精细化电离层模型是十分必要的。

1 数据来源及其分析方法

1.1 数据来源

本文在建立中国区域电离层模型时，采用CMONOC观测站的观测数据，利用数据格式转换、元数据编辑及数据质量检查（translation, editing and quality checking, TEQC）软件进行数据预处理，处理时的采样间隔设为30 s，卫星截止高度角度为10°，电离层的薄层高度设置为400 km，时空分辨率分别为1 h、2.5°×2.5°，采用15阶球谐函数建立中国区域电离层拟合模型，建模时使用的站点分布图如图1所示。

图1 CMONOC站点分布图

建立中国区域电离层模型时，选择选择原始观测数据质量较好，时间连续性较强的测站，测站尽可能均匀覆盖整个中国区域，其技术路线如图2所示。图2中DCB（differential code bias）为差分码偏差，亦称为硬件延迟偏差；STEC（slant total electron content）为倾斜路径总电子含量。

图2 建立中国区域电离层模型技术路线

首先对CMONOC原始观测数据进行预处理，采用宽巷组合法进行异常值剔除、周跳修复，然后采用双频GPS 载波相位平滑伪距方法获取TEC观测量[11]。如果在电离层建模时没有考虑硬件延迟的影响，将会对建模结果产生非常严重的系统偏差，所以在建立中国区域电离层模型时，需要对硬件延迟偏差进行解算，然后对电离层穿刺点（ionospheric pierce point, IPP）、STEC和VTEC进行解算，即可得到中国区域电离层模型，最后对建立的中国区域电离层模型进行精度评估，球谐函数的阶数会影响中国区域电离层模型产品的精度，综合考虑精度和计算速度等因素，本文使用15阶球谐函数建立中国区域电离层模型[12-14]。

1.2 双频GPS数据获取TEC的原理

基于双频GPS观测数据建立中国区域电离层模型时，采用伪距观测值来解算STEC，为提高伪距观测值的精度，采用相位平滑伪距法，可得斜路径总电子含量STEC为

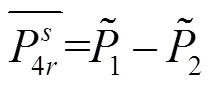
1.3 球谐函数数学模型

球谐函数数学模型是利用球谐展开级数函数来描述单层电离层模型的，基于球谐函数建立中国区域的电离层模型，能较好地反映中国区域上空总电子含量的时空分布特征，VTEC球谐函数模型表达式[15]为

2 结果分析

2.1 球谐函数模型对比分析

借助2018年年积日第1—31天CMONOC的观测数据，首先进行数据预处理，利用载波相位平滑伪距的方法提取电离层延迟观测量。建立模型过程中，将每颗卫星的DCB作为未知参数来求解，由于同一接收机和卫星间的延迟误差相对稳定，在一段时间内基本保持不变，因此在解算时，可将一天内的DCB作为一个常数[16-18]，求解的结果可以反映建立模型稳定性和精度。对建立的中国区域电离层模型解算的PRN1-32号卫星DCB与CODE的偏差进行比较，其结果如图3所示，接收机DCB如图4所示。

图3 解算的卫星DCB与CODE中心参考值间的偏差

图4 接收机的DCB

由图3可知：32颗卫星的DCB的偏差都在0.4 ns以内，表明解算卫星的DCB是稳定的、精度是有保证的。

由图4可知，在100个参与建模的测站中，解算测站接收机的DCB基本在0.3 ns内，总体在0.4 ns内，表明接收机的DCB是稳定的、可靠的。图5给出PRN 1号卫星31天的DCB与CODE中心公布的参考值间的偏差。

由图4可知，PRN 1号卫星31天的DCB与CODE中心参考值间的偏差在0.3 ns以内，进一步证明在建立中国区域电离层模型过程中，解算的DCB是稳定的、可靠的。本文在建立中国区域电离层模型时，采用CMONOC观测站的观测数据，利用数据格式转换、元数据编辑及数据质量检查（translation, editing and quality checking, TEQC）软件，对年积日第1天中国区域电离层模型格网VTEC和CODE全球电离层模型格网VTEC的残差统计分析，结果表明残差进行在[-22]内，其格网VTEC值接近CODE发布的VTEC值，考虑到CODE全球电离层模型的参考精度为2~8个TECu（1个TECu表示“1×1016个电子/平方米”），且在中国区域的模型精度较低，因此，基于CMONOC数据建立的中国区域电离层模型精度是有保证的。

图5 PRN 1号卫星的DCB与CODE中心参考值间的偏差

2.2 COMONOC数据数量对建模结果的影响分析

为对比分析观测数据数量对模型精度的提升效果，建立模型时，分别采用100个测站、200个测站的观测数据进行建模，站点分布图如7所示。当使用100个测站观测数据建立中国区域电离层模型（IONEX1模型）时，使用三角符号表示测站；当使用200个测站观测数据建立中国区域电离层模型（IONEX2模型）时，使用三角符号和圆圈符号表示测站。

图6 建模使用的测站分布示意

采用100个测站、200个测站的观测数据进行建模后，将其得到的结果与CODE中心参考值进行对比分析，结果如图7和表1所示。

图7 2018年年积日第1天不同时刻两种电离层模型与CODE中心参考值间的偏差

表1 2018年年积日第1天两种电离层模型与CODE中心的偏差统计表

从图7和表1可以看出：200个测站建立的中国区域电离层模型，在全天任意时刻的RMS均小于100个测站建立的中国区域电离层模型；当测站数量为100时，电离层模型产品与CODE中心的偏差的平均值（MEAN ）为0.48个TECu，均方根（root mean square, RMS）为1.45个TECu，标准差（standard deviation, STD）为1.22个TECu；当测站数量为200时，MEAN 为0.35个TECu，RMS为1.12个TECu，STD 为0.82个TECu。这表明，建模时采用的测站数据越多，获取穿刺点的位置就越多，建模精度越高。如何对区域大小与测站数量的选取，在满足高效的同时又可以获取较高的精度，还需要进一步研究。

3 结束语

本文借助CMONOC GPS原始观测数据，基于球谐函数建立中国区域电离层模型，对建立模型的精度进行了评估，得到以下结论：

1）基于2018年1月1日CMONOC观测数据建立中国区域电离层模型，解算32颗卫星的DCB的标准差都在0.4 ns以内，第PRN 1号卫星31天的DCB与CODE中心参考值间的偏差在0.3 ns以内，表明解算卫星的DCB是稳定的、精度是有保证的。

2）对建立的电离层模型与CODE中心发布全球电离层模型进行对比分析，VTEC残差在[-22]内，考虑到CODE模型在中国区域精度较差，基于CMONOC数据建立的中国区域电离层模型的精度是可以满足要求的。

对比分析不同测站数量与模型精度的关系，采用的测站数量较多，建立模型的精度也就较高；从时空分辨率来看，建立模型的时空分辨率优于CODE全球电离层模型。

[1]章红平, 平劲松, 朱文耀, 等. 电离层延迟改正模型综述[J]. 天文学进展, 2006, 24(1): 16-26.

[2]ELSOBEIEY M, EL-RABBANY A. Impact of second-order ionospheric delay on GPS precise point positioning[J]. Journal of Applied Geodesy, 2011, 5(1): 152-164.

[3]WANG N, YUAN Y, LI Z, et al. Improvement of Klobuchar model for GNSS single-frequency ionospheric delay corrections[J]. Advances in Space Research, 2016, 57(7): 1555-1569.

[4]张好. 区域电离层模型的建立及精度分析[D]. 郑州: 信息工程大学, 2011.

[5]JIAO W H, GENG C J, MA Y H, et al. A method to estimate DCB of COMPASS satellites based on global ionosphere map[J]. Lecture Notes in Electrical Engineering, 2012, 159(5): 347-353.

[6]张小红, 李征航, 蔡昌盛. 用双频GPS观测值建立小区域电离层延迟模型研究[J]. 武汉大学学报(信息科学版), 2001, 26(2): 140-143, 159.

[7]袁运斌. 基于GPS的电离层监测及延迟改正理论与方法的研究[D]. 武汉: 中国科学院研究生院(测量与地球物理研究所), 2002.

[8]张瑞. 多模GNSS实时电离层精化建模及其应用研究[D]. 武汉: 武汉大学, 2013.

[9]陈鹏, 陈家君. GPS/GLONASS融合的全球电离层格网模型结果分析[J]. 大地测量与地球动力学, 2014, 34(5): 70-74.

[10]王泽民, 王康, 李航, 等. 南极电离层特征的球冠谐分析[J]. 测绘科学, 2018, 43(10): 33-38.

[11]SCHENEWERK M. A brief review of basic GPS orbit interpolation strategies[J]. GPS Solutions, 2003, 6(4): 265-267.

[12]薛军琛. 中国地区电离层延迟函数模型建立与精度估计[D]. 青岛: 山东科技大学, 2010.

[13]魏传军. 基于地基GNSS观测数据的电离层延迟改正研究[D]. 西安: 长安大学, 2014.

[14]袁浩鸣. GNSS区域电离层建模与精度分析[D]. 徐州: 中国矿业大学, 2019.

[15]李新星. 基于球谐函数构建VTEC模式与精度分析[D]. 武汉: 中国地震局地震研究所, 2017.

[16]CHEN K, GAO Y. Real-time precise point positioning using single frequency data[EB/OL]. [2020-05-18]. https://www.cambridge.org/core/services/aop-cambridge-core/content/view/AAF9050AC5359A721E307B4789336F12/S0373463313000039a.pdf/single-frequency-ionosphere-free-precise-point-positioning-using-combined-gps-and-glonass-observations. pdf.

[17]房成贺, 陈俊平, 兰孝奇, 等. 基于BDS/GPS观测的北斗硬件延迟解算[J]. 测绘科学技术学报, 2018, 35(1): 32-37.

[18]AMIRI-SIMKOOEI A R, ASGARI J. Harmonic analysis of total electron contents time series: methodology and results[J].GPS Solutions, 2012, 16(1): 77-88.

Modeling and accuracy evaluation of ionosphere in China

CHEN Yonggui

( Henan Collage of Surveying and Mapping, Zhengzhou 451464, China)

In this paper, based on the original Global Positioning System (GPS) data of Crustal Movement Observation Network of China (CMONOC) reference station and spherical harmonic function, the ionosphere model of China is established. The experimental results show that the standard deviation of Different Code Bias (DCB) of 32 GPS satellites calculated in the model is stable at 0.4 ns, the overall deviation of DCB and code is stable at 0.3 ns, and the residual error of Vertical Total Electron Content (VTEC) value of the new model and that of code is stable in the range [-22]. The comparison shows that the influence of the number of CMONOC stations on the modeling results is analyzed. The accuracy of modeling can be improved by increasing the number of stations.

Crustal Movement Observation Network of China; spherical harmonic function; total electron content; different code bias

P228

A

2095-4999(2021)02-0104-05

陈永贵. 中国区域电离层建模及其精度分析[J]. 导航定位学报, 2021, 9(2): 104-108.（CHEN Yonggui. Modeling and accuracy evaluation of ionosphere in China[J]. Journal of Navigation and Positioning,2021,9(2): 104-108.）

10.16547/j.cnki.10-1096.20210216.

2020-06-14

河南省高等学校重点科研项目（20B170002）。

陈永贵（1979—），男，吉林辽源人，硕士，副教授，研究方向为工程测量理论与方法、GNSS测量与数据处理。