一种热电偶温度采集装置的优化设计

2021-04-20王晨辉赵冬青贾兴中陈建军

电子设计工程 2021年6期

王晨辉，赵冬青，贾兴中，陈建军

（中北大学电子测试技术国家重点实验室，山西太原 030051）

在航天和工业领域中，温度的监测至关重要。在温度采集时，要求传感器有较大的量程、较好的抗干扰性以及较高的测量精度和稳定性[1]。热电偶具有测温范围广、测量精度高、耐压性能好等特点，其中K 型热电偶更具有成本较低、实用性强等优点，被广泛应用到航天和工业的各种测温环节中[2]。但同时热电偶又会由于冷端温度不稳定和“温度-热电势”关系的非线性使测量温度产生较大的偏移量[3]。该设计通过硬件冷端补偿和软件非线性校正，提高了K 型热电偶测温的准确性和稳定性。通过设计了一款四通道热电偶温度采集装置验证了该优化设计在-30～1 300 ℃的量程内，测量误差小于0.5 ℃。

1 硬件电路组成

热电偶温度采集装置硬件电路由AD8495 冷端补偿电路、分压跟随电路、二阶压控低通滤波电路、单片机ADC 转换电路、串口转422 电路组成，如图1所示。AD8495 对K 型热电偶的输入热电势进行冷端补偿；分压电路将经AD8495 放大的电压分压至2.45 V 以下，以满足AD 转换要求；跟随电路将前端调理电路与后端电路隔离开，后端电路所产生的干扰并不会影响前端调理电路；二阶压控低通滤波用以滤除线路串扰噪声；单片机将采集的模拟量转换为数字量并通过串口发送至ADM2682E，将串口数据转换为422 接口协议的数据，通过接收设备发送至上位机进行非线性校正。

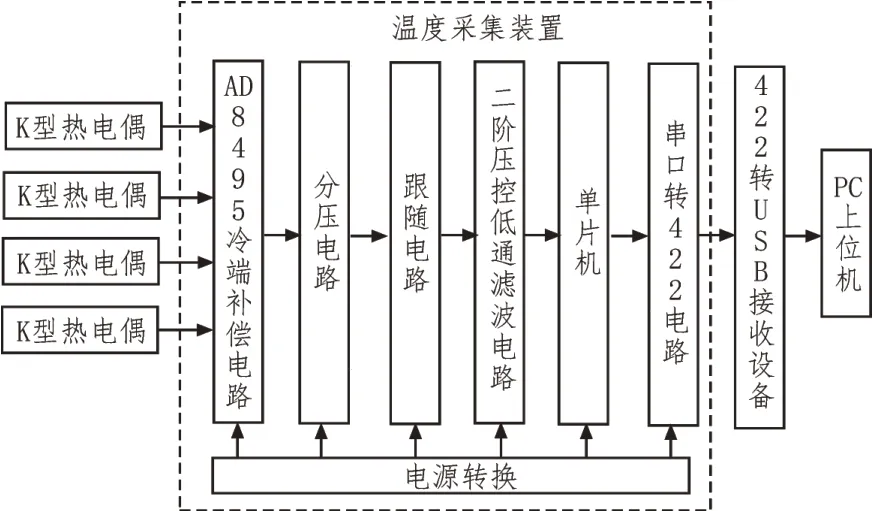
图1 电路组成

2 电路设计

2.1 AD8495冷端补偿电路设计

AD8495 是一款集成K 型热电偶参考冷端结点温度补偿的精密仪表放大器，内部电路如图2 所示，其内部集成了一个温度传感器来进行冷端温度补偿；通过内部集成的三运放仪表放大器提供了一个122.4 倍的固定增益来放大热电偶的微小信号[4]。仪表放大器的高共模抑制比极大地降低热电偶引线以及其他原因可能引入的共模噪声。仪表放大器的高输入阻抗特性还能允许在输入端添加额外的输入滤波电路。同时，在连接器与电路板连接处的连线选用热电偶补偿导线，使进入测量设备的电压信号可以近似等于测量节点热端所产生的热电势[5]。

图2 AD8495内部电路组成

热电偶的传输热电势在输入时，常会引入很多高频噪声。如果噪声不被滤除，就会表现为温度信号的波动[6]。通过在放大器前端设置射频滤波电路来消除高频干扰，RF 滤波电路设计图如图3 所示。

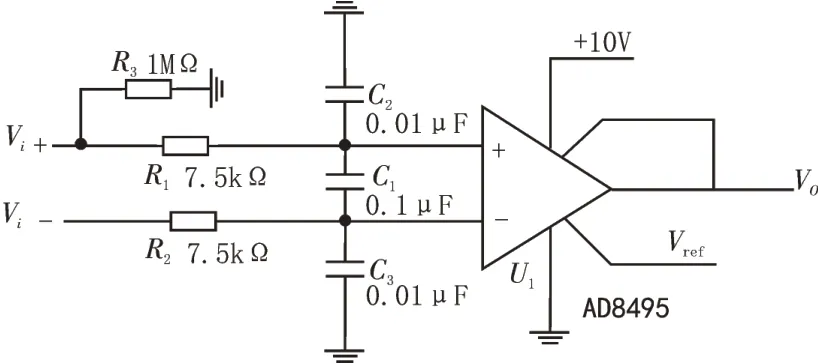
图3 RF滤波电路设计

由于仪表放大器的高输入阻抗特性，热电偶的电势经R3流到地平面，从而不会流向滤波电路的电阻，电容C1能匹配两路RC滤波器，防止电容不匹配导致的共模抑制比衰减。

其差模截止频率：

其共模截止频率：

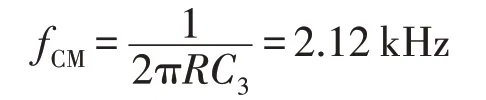
此电路对大于101.1 Hz 的差模信号以及大于2.12 kHz 的共模信号有较好的抑制，有效地减少了高频噪声对低频温度信号的干扰。

2.2 分压跟随电路设计

热电偶的温度信号经AD8495 补偿后的电压不满足后端单片机AD 采样的输入电压要求，这就需要将电压调整到C8051F352 内部AD 采样基准电压（2.45 V）范围内，以便后端AD 采样。图4 所示为温度采集装置的分压跟随调理电路。K 型热电偶的测温范围在-20～1 300 ℃，AD8495 能产生122.4 倍的固定增益，AD8495 的基准电压为0.483 V，所以AD8495 的输出电压范围为0.388～6.988 V，经分压电路以及后端二倍放大电路后的输出电压范围为0.132～2.382 V，满足后端AD 采样的要求。分压后，经过跟随电路，跟随电路具有高输入阻抗和低输出阻抗的特点，可消除前后端电路的相互干扰[7]。另外需在运放的电源和地端串接0.1 μF 退耦电容消除耦合干扰。

图4 分压跟随电路设计

2.3 二阶压控低通滤波电路设计

热电偶温度信号和大多温度信号相同，响应时间较长，由于信号改变缓慢，所以必须进行滤波来消除线路串扰噪声[8]。在冷端补偿之后，需要设置滤波电路来消除线路串扰噪声[9]，并对信号进行二倍放大，使满量程时的电压范围接近ADC 的参考电压，以提高模数转换的精度，二阶压控低通滤波电路如图5所示。

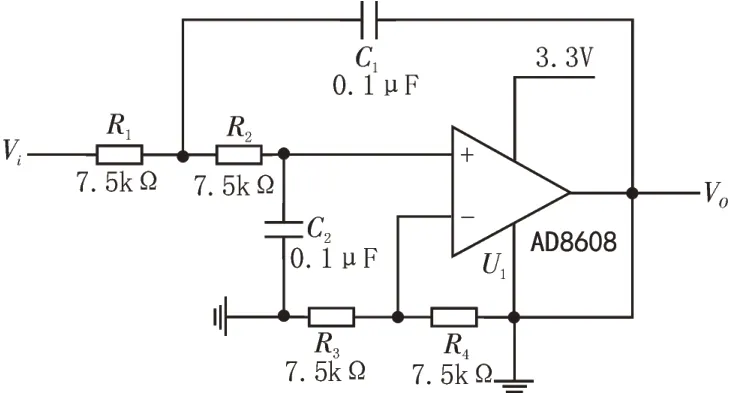
图5 二阶压控低通滤波电路设计

当R1=R2=R、C1=C2=C时，滤波器的传递函数：

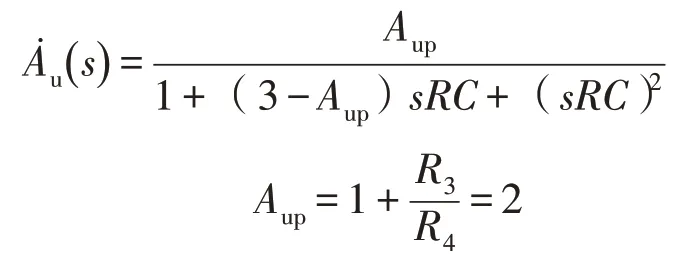
令式中s=jω，ω=2πf、f0=1/2πRC，得出电压放大倍数：

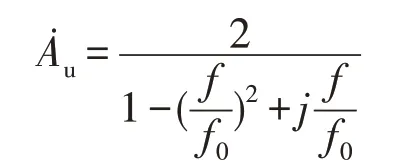
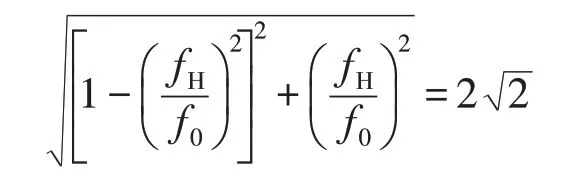
该滤波器上限截止频率/(2πRC)=284.89 Hz，其幅频特性仿真如图6所示。

图6 低通滤波截止频率仿真

2.4 单片机AD采样电路设计

该设计采用C8051F352单片机作为设备的主控芯片，它是完全集成的系统级MCU，片内有一个16 位Sigma-Delta 模/数转换器（ADC），该ADC具有在片校准功能。它的优点是最小系统外围电路小，占用电路空间小，单电源供电，功耗小[10]。单片机电路如图7所示。

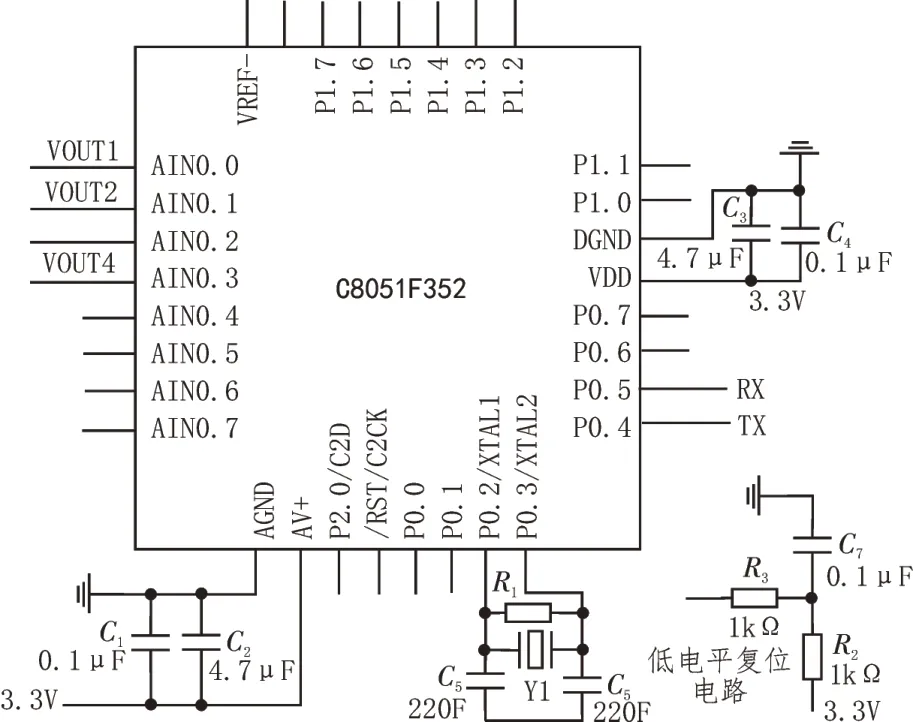
图7 单片机电路设计

供电电路由LT1763-3.3芯片产生3.3 V电压为单片机供电，在地与VDD之间增加一大一小两只电容来滤除电路中的耦合干扰，为芯片提供一个干净的供电电压[11]。

3 软件非线性校正

非线性指的是两个变量的函数关系，不是一种简单的线性比例关系。热电偶电动势的改变随着温度的变化就是非线性的，因此需要设计一种算法来消除热电偶的非线性[12]。

3.1 分段线性拟合

K 型热电偶是一种在分段温度下，热电势与温度近似呈线性的一种温度测量仪表[13]。将热电偶“温度-热电势”的关系进行分段线性拟合，分段拟合结果如图8 所示。

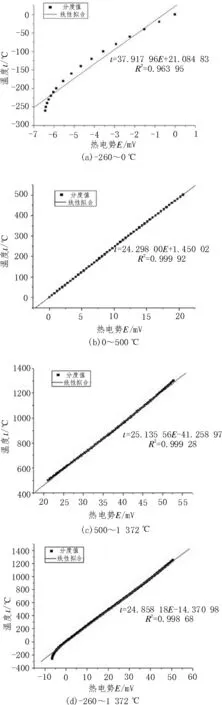
图8 热电偶“温度-热电势”关系线性拟合

拟合结果表明，热电偶温度与热电势的关系在0～500 ℃、500～1 372 ℃区间内线性度较好，但是在0 ℃以下有较大的非线性，导致热电偶在全温度测量范围存在较大的非线性。因此通过对-260～0 ℃、0～500 ℃、500～1 372 ℃进行分段拟合来达到非线性校正的作用[14]。通过将数据带入线性回归方程验证分段线性校正的准确度，拟合结果对比如图9所示。

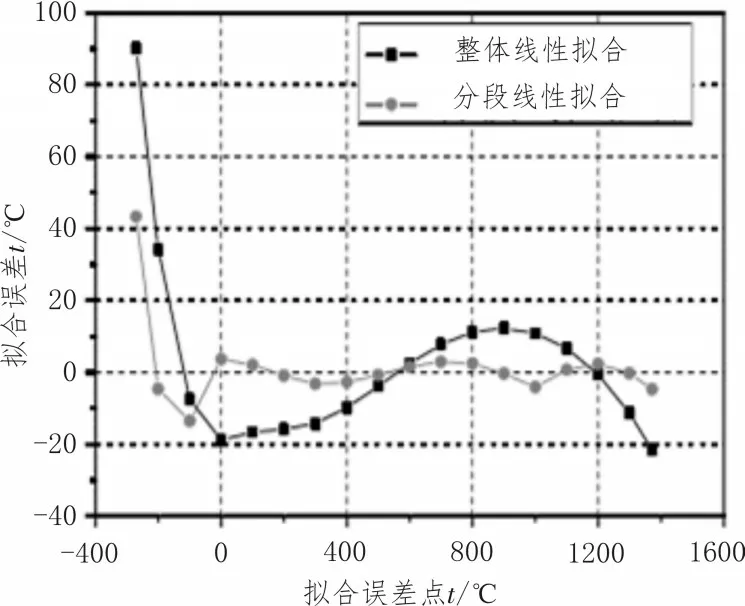
图9 整体拟合与分段拟合结果对比

通过对结论的分析可知，分段标定前最大误差达到90 ℃，而分段标定后误差减小为40 ℃，所以分段标定对于采集精度有明显提高，但使用分段标定拟合出的结果并不能切合热电偶温度与热电势的变换曲线[15]，因此只适用于对测温精度要求不高的场合中，无法满足设备的精度要求。

3.2 最小二乘法多项式拟合

通过对分段线性标定结果的分析，需要计算一个与“温度-热电势”关系更加切合的回归方程来尽可能提高温度的采集精度。最小二乘法是通过数理统计原理求取变量之间回归方程的一种统计方法[16]。在给定的一组离散数据(xi,yi),i=0,1,…,n中找寻一个函数：，使得。

对热电偶温度与热电势的关系进行分段多项式拟合，得出的系数如表1所示。通过将热电势分别带入分段线性拟合公式和最小二乘法多项式拟合公式内，验证其准确度，K 型热电偶的输入电压为41.276 mV，经查询分度值可知其温度为1 000 ℃，带入多项式拟合公式内，其结果为1 000.26 ℃，误差为0.26 ℃，带入图8（b）中分段线性拟合公式内，其结果为995.33 ℃，误差为4.67 ℃，出现这种误差的原因为在标定温度范围内，温度的变化是非线性的，而线性拟合忽略了这种微小误差，导致线性拟合的结果与实际结果并不相符，所以通过最小二乘法多项式进行非线性校正极大地提高了温度采集装置的精度。

4 实验分析与测试

在完成硬件电路和单片机程序设计后，为了验证该设计的测量精度和可靠性，利用Omega 公司的CL3515R 系列温度校准仪模拟热电偶在各个温度段下输出的模拟电压信号供设备采集，后通过计算机对采集数据进行存储。试验中同时对四路提供不同温度的模拟信号，验证采集装置的准确性与可靠性，试验结果如图10 所示。实验结果表明，设备的采集精度可达到±0.5 ℃，且各路间信号并无干扰。