基于综合分段优势的植被覆盖度模型比较
2021-04-20边慧芹王雪梅
边慧芹,王雪梅,2
(1. 新疆师范大学地理科学与旅游学院,新疆 乌鲁木齐 830054;2. 新疆干旱区湖泊环境与资源重点实验室, 新疆 乌鲁木齐 830054)
植被作为极其重要的自然环境要素,一般用植被覆盖度来表示。植被覆盖度(vegetation coverage, Fc)可综合表述为植被地上部分在单位面积内的垂直投影占区域总面积的百分比[1]。植被覆盖度在评估水土保持、改善水文状况、调节径流、防止沙漠化及水土流失等方面发挥着重要意义[2]。其变化不仅能够量度地表植被生长发育情态,还能够反映生态系统变化状况[3]。植被覆盖度反演方法大致可分为地表实测方法和遥感监测方法,地表实测方法又分为目估法、采样法和仪器法(数码照相法)。目估法准确度受人为因素影响较大,因绝对误差较高而不适宜用于植被覆盖度监测[4]。虽然数码照相法、采样法预测植被覆盖度具有一定精度[5-6],但数码照相法易受外界环境条件制约,而采样法测量过程费时费力,仅适合估算较小区域的植被覆盖度。遥感技术以其简捷迅速、无破坏性及节省人力物力等优点,为大范围的植被覆盖度反演提供可能,其中较为常用的遥感监测方法有植被指数法、像元分解模型法、FCD (forest canopy density mapping model)模型法和回归模型法[7-10]。
杨胜天等[11]利用植被指数法反演植被覆盖度并分析其变化,对近20 年黄河流域生态保护工作进行了初步评估。由于植被指数法易受大气、土壤、地貌等影响,且植被指数只能反映植被覆盖度的趋势,并不能代表实际植被覆盖度,因此其预测精度有待提高。魏石磊等[12]、陈效逑和王恒[13]通过像元分解模型估测特定区域植被覆盖度,发现此方法具有较高的估测精度。Carlson 和Ripley[14]、温小乐等[15]发现利用像元二分模型的平方反演植被覆盖度在中低植被覆盖地域更贴近实测数值,但总体精度低于像元二分模型。马中刚等[16]选取16 种植被指数利用逐步回归法及线性混合像元分解法构建荒漠化地域植被覆盖度反演模型发现此方法反演结果较为贴近现实,但还需进一步提高估测精度。王云[17]选用不同植被指数利用分段回归模型法反演植被覆盖度,发现此方法在一定程度上能够解决饱和性问题,并具有较高精度。FCD 模型(forest canopy density mapping Model)能够综合裸土指数、阴影指数及植被指数构建复合指数代入像元二分模型反演植被覆盖度,削弱了裸土、植被阴影及城市用地对反演结果的影响,此方法考虑现实问题且综合像元二分方法的运用,所得精度普遍高于对应的单独植被指数[10]。
目前,已有的研究大多通过单一植被指数带入或构建模型进行植被覆盖度反演[16],但植被光谱常因植被所处环境、生长状态、大气因素等影响变化而具有一定时效性与区域性,且所选取的最优植被指数也会产生变化。因此,根据不同植被指数特点,采用分段方式在不同植被覆盖度区间选取最优植被指数联合预测植被覆盖度,能够有效提高反演精度。本研究选择处于干旱与极端干旱区且地表植被构成较为复杂的渭干河-库车河三角洲绿洲作为研究区,在前人研究的基础上选取9 种植被指数,结合野外实测植被覆盖度数据进行相关性分析,通过敏感植被指数并基于分段方式采用回归模型及FCD 模型对研究区植被覆盖度进行反演,为干旱区植被覆盖度定量监测及生态环境评价工作开展提供一定依据。
1 数据来源与研究方法
1.1 研究区概况
渭干河-库车河三角洲绿洲处于新疆维吾尔自治区境内,是塔里木盆地北麓较为典型及完整的形似扇形的平原绿洲,空间方位在39°30′ − 42°40′ N,81°27′ − 84°07′ E,区域由库车市、沙雅县与新和县构成。该区域是大陆性暖温带干旱气候,具有风沙肆虐、夏日干热、冬日干冷,日照时间长,蒸发强度大,昼夜温差大,降水稀少且分布不均匀的特性。年均气温介于10.5~14.4 ℃,年均降水量介于50.0~66.5 mm,年均蒸发量在2 000 mm 以上。该区域依靠由中高山地域沿途流下的塔里木河、渭干河、库车河河水进行灌溉,以种植业为经济主体产业,主要种植棉花(Gossypium spp.)、红枣(Ziziphus zizyphus)、玉米(Zea mays)等,地表植被组成较为复杂,盐渍化现象普遍,常见耐盐植被有柽柳(Tamarix chinensis)、盐穗木(Halostachys caspica)及盐节木(Halocnermum strobilaceum)等。
1.2 数据来源与处理
本研究采用的遥感数据来自具有11 个波段、空间分辨率为30 m、全色波段分辨率提高至15 m、接收时间为2019 年7 月26 日的美国陆地卫星Landsat 8-OLI。因传感器自身会产生误差,需在ENVI 5.1 软件中进行辐射定标,将DN (原始灰度)值转化成大气顶层辐射亮度来消除误差;然后利用FLAASH 模块进行大气校正,消除大气、光照变化等原因对地物反射的干扰以获得较为真实的地物反射率,最后使用Band Math 工具计算各植被指数,并利用SPSS 22.0 软件的相关分析工具分析不同植被指数与实测植被盖度间的相关关系。
2019 年7 月在研究区布设样地99 个并进行实地调查(图1),不含水体及城市建设规划用地,样地大小设计为50 m × 50 m。该区域地表植被构成复杂,在每个样地内选取5 个1 m × 1 m 的草本样方,在东西南北四角设置10 m × 10 m 的植被样方,对样方内植被个数及其东西、南北方向植被冠幅进行测量,计算得到植被覆盖度值;然后利用1 m × 1 m、10 m ×10 m 植被样方对50 m × 50 m 植被样方进行估测计算,得到总样方植被覆盖度,并对样方所处环境的地貌特点、地表植被种类及组成等数据进行记录。本研究采用分层抽样方法将实测数据分为两组,一组79 个用于建模,另一组20 个用于验证。

图1 研究区采样点分布图Figure 1 Distribution of sampling points in the study area
1.3 植被指数选取
选取较为常用的9 种植被指数并划分为3 类:
Ⅰ. 简单差值及比值植被指数:差值植被指数(DVI)、比 值 植 被 指 数 (RVI)、归 一 化 植 被 指 数(NDVI)、绿色归一化差值植被指数 (GNDVI)和近红外光百分比植被指数 (IPVI)。
Ⅱ. 抑制土壤背景因素干扰的植被指数:二次改进型土壤调节植被指数(MSAVI)和优化土壤调节植被指数 (OSAVI)。
Ⅲ. 增添大气修正元素的植被指数:大气阻抗植被指数 (ARVI)和增强植被指数 (EVI)。
各植被指数具体计算公式如表1 所列[18-26]。
1.4 饱和性分析
在不同植被覆盖度等级利用不同植被指数进行反演可以提高估测精度。为了解植被指数特征及判断各植被指数跟随植被覆盖度变化的饱和点,利用分段变化量、分段百分比实行饱和性分析。
分段变化量是不同植被指数在各自植被覆盖度范围的变化量(Si),分段百分比是不同植被指数在各自植被覆盖度范围所占的比例(Ti)。计算公式如下[17]:
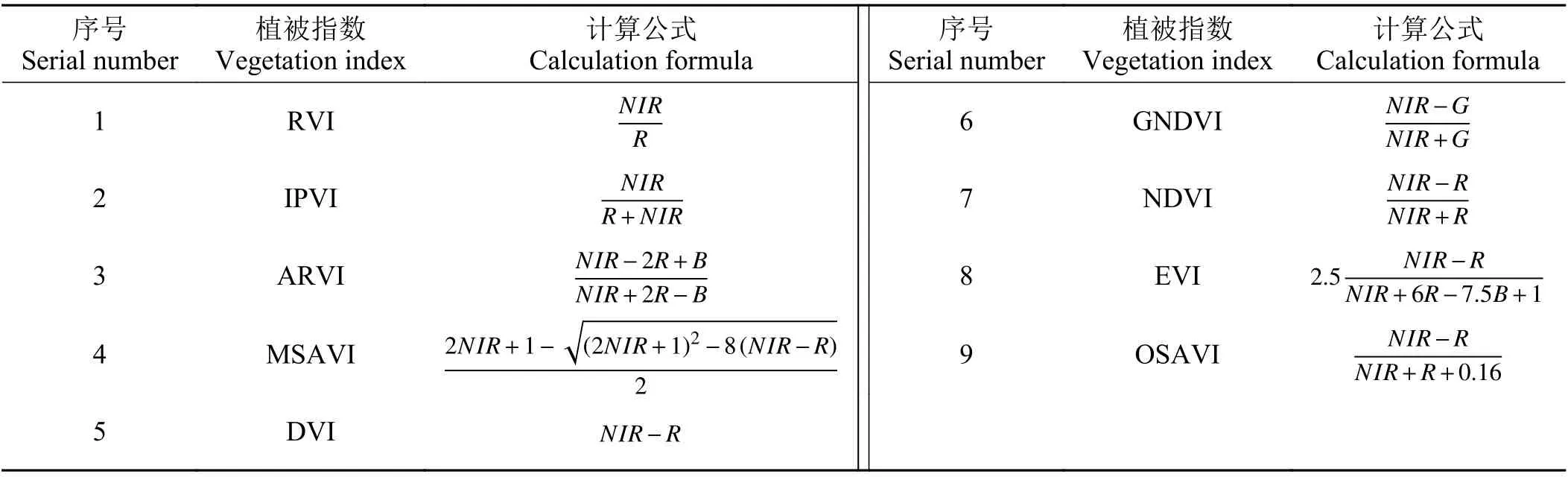
表1 植被指数计算Table 1 Calculation of vegetation indices

式中:Si是植被覆盖度为i 时的分段变化量;max(VIi)、min(VIi)分别为在某一植被覆盖度i 时植被指数所取得最大值和最小值。

式中:Ti为植被覆盖度为i 时的分段百分比;VIi是植被覆盖度在i ± 0.005 内所对应的植被指数均值;max(VI)、min(VI)分别为植被指数均值的最大值和最小值。
1.5 FCD 模型
FCD 模型是利用植被指数(vegetation index, VI)、裸土指数(bare-soil index, BI)及阴影指数(shadow index, SI)构成复合指数(vegetation bare-soil shadow index, VBSI)代入像元二分模型对植被覆盖度进行估测的模型,其优点是可以消除或减弱遥感影像中阴影或裸地等对植被的影响,进一步提高地表植被覆盖度预测精度。公式如下[27-28]:

式中:VI 为植被指数,BI 为裸土指数,SI 为阴影指数,VBSI 为复合指数,B 为蓝波段反射率值,G 为绿波段反射率值,R 代表红波段反射率值,NIR 为近红波段反射率值,SWIR 为短波红外波段反射率值,n 为−0.1。VBSIsoil是实测裸土样点所对应的VBSI 取值(累计频率接近5%),VBSIveg是实测纯植被覆盖样点所对应的VBSI 取值(累计频率接近98%)。
1.6 模型精度评估
为检验各个植被覆盖度反演模型的准确度,检测实测植被覆盖度与估测植被覆盖度间的误差情况,选取总体决定系数(R2)、均方根误差(RMSE)及预测精度(PRECISION)进行模型精度评价。决定系数越大,变量间联系越紧密;均方根误差越小,预测精度越大,说明模型预测精度越高。

式中:ABS 为绝对值,yi为样本实测值;为样本估测值;为样本平均值;n 是样本总量。
2 结果与分析
2.1 植被指数和实测植被覆盖度相关关系分析
不同植被指数与实测植被覆盖度显现出极显著正相关关系(P < 0.01) (表2),说明可以利用其反演植被覆盖度。植被指数中MSAVI 与实测植被覆盖度的相关性最高,为0.917;其次为NDVI、OSAVI、IPVI、GNDVI;RVI 最低,为0.668。

表2 实测植被覆盖度与植被指数的相关性Table 2 Correlation between measured vegetation coverage and vegetation indices
2.2 植被覆盖度分段点的选定
为研究植被指数特征及判断各植被指数跟随植被覆盖度变化的饱和点,计算不同植被指数的分段百分比。RVI 累积分段百分比约20%时植被覆盖度在0.5 左右,说明RVI 在植被覆盖度小于0.5 时分辨率较低;植被指数NDVI、IPVI、OSAVI 因公式中的分子、分母随植被覆盖度的增大而增加使得总体差异较小,所对应的植被覆盖度大致相同(图2)。
在0.0 ≤ Fc≤0.3 时,不同植被指数间分段百分比变化较一致,且大多数植被指数累积百分比在20%左右;在0.3 < Fc≤0.7 时,各植被指数的变化幅度也较一致,大部分植被指数累积百分比接近70%;在0.7 <Fc≤1.0 时,9 种植被指数变化幅度较大,所以本研究选取0.3 和0.7 作为反演植被覆盖度的分段点。
2.3 基于分段回归的植被覆盖度反演模型
2.3.1 分段回归模型最优植被指数选取
通过计算Fc≤0.3、0.3 < Fc≤0.7 及0.7 < Fc≤1共3 段区间内不同植被指数与实测植被覆盖度间的分段相关值、分段累计变化量及分段累计百分比,可得到各植被指数分段综合分析表(表3)。从不同植被指数与实测植被覆盖度的分段相关值可以得出,在不同区间内各个植被指数和植被覆盖度均具有较好的相关性。由于利用植被指数分段反演植被覆盖度存在像元重合或缺失的问题,综合分段相关性高、分段累计变化量较小及分段累计百分比较高的条件,选定MSAVI 对 [0.0, 0.3]内的植被覆盖度进行反演,选定GNDVI 对 (0.3, 0.7]内的植被覆盖度进行反演,选定IPVI 为植被覆盖度 (0.7, 1.0]内的最佳反演植被指数。
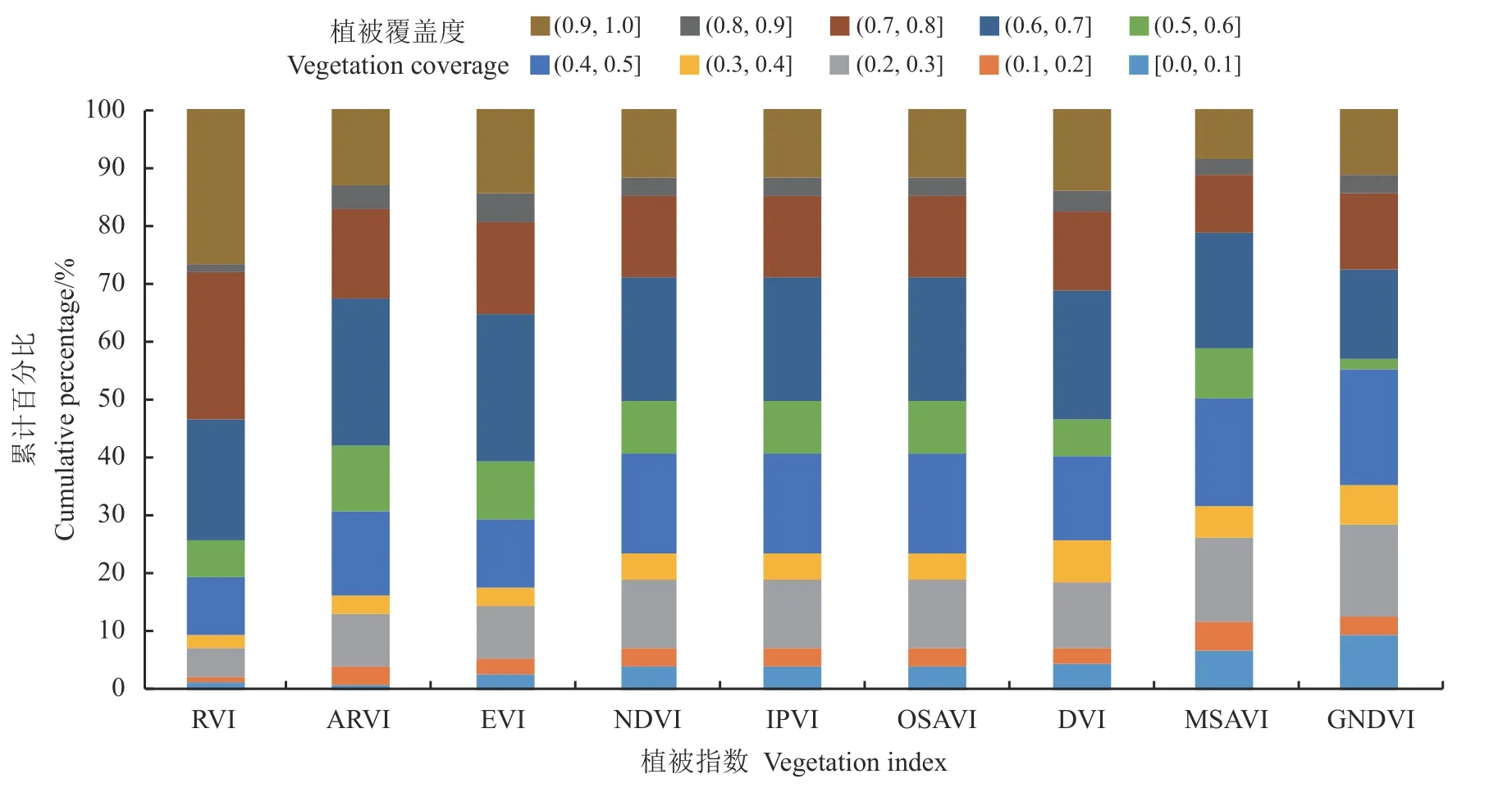
图2 植被指数与植被覆盖度分段百分比Figure 2 Vegetation indices and the segmented percentage of vegetation coverage
2.3.2 分段回归模型建立
选取线性函数、对数函数、倒数函数、二次多项式及三次多项式建立各段实测植被盖度与最优植被指数的回归模型。各分段最优植被指数与实测植被覆盖度建模结果基本符合统计学要求(表4)。各分段最优植被指数选取三次多项式模型反演植被覆盖度最优,F 检验达到0.01 水平,因此本研究选取MSAVI、GNDVI、IPVI 用三次多项式分段反演植被覆盖度。其中,因植被指数分段组合中MSAVI与GNDVI 在0.0 ≤ Fc≤0.3 时分段点接近,在预测植被覆盖度时没有出现像元缺失和重复的现象,GNDVI与IPVI 在植被覆盖度0.7 处存在像元重复现象,需要对GNDVI 在0.59~0.61 取值范围与IPVI 做平均像元处理,使预测效果更好。

表3 各植被指数分段综合分析Table 3 Comprehensive analysis of the different vegetation indices
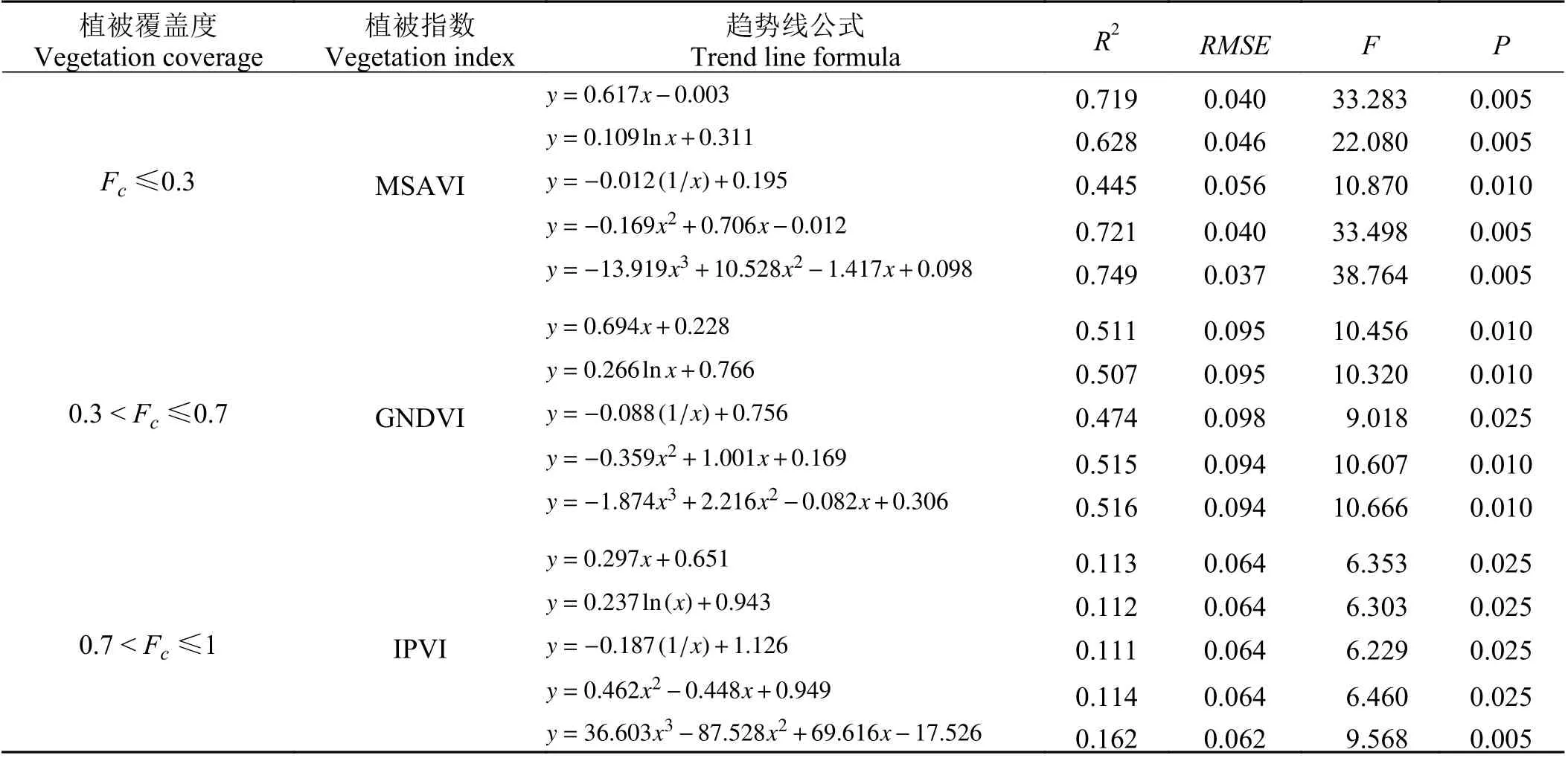
表4 分段回归植被覆盖度模型Table 4 Vegetation coverage model based on segment regression
2.4 综合分段优势的FCD 反演模型
利用不同植被指数采用分段回归方法构建植被覆盖度模型可以消除饱和性、土壤、地表状况等因素的影响以提高植被覆盖度预测精度,因此采用不同复合植被指数代入FCD 模型,选取最优复合植被指数所在的FCD 模型分段反演植被覆盖度理论上也可以提高预测精度。利用图2 结果将0.3 和0.7 作为植被覆盖度分段点,选取决定系数(R2)、均方根误差(RMSE)及预测精度(PRECISION)分段讨论各植被指数代入FCD 模型的预测精度,使用各段模型精度最高的植被指数反演植被覆盖度对FCD 模型进行优化。对比各段FCD 模型决定系数、均方根误差及预测精度可以发现(表5):在0.0 ≤ Fc≤0.3 时,NDVI 及OSAVI 预测植被覆盖度的精度最高,而复合MSAVI 在此段的精度较低,在0.3 < Fc≤0.7 时,GNDVI 与MSAVI 预测植被覆盖度的精度最高,在植被覆盖度大于0.7 时,MSAVI 预测植被覆盖度的精度最高,再次说明利用MSAVI 预测中,高植被覆盖度具有较高的精度,而在预测较低植被覆盖度时精度较弱。由于NDVI 与OSAVI 预测精度相同,但NDVI 在植被覆盖度研究中应用更为广泛及预测结果稳定,因此选定NDVI 对[0.0, 0.3]内的植被覆盖度进行反演,选定MSAVI 对(0.3, 0.7]及(0.7, 1.0]内的植被覆盖度进行反演。

表5 FCD 模型各分段植被覆盖度精度分析Table 5 Analysis of vegetation coverage accuracy in each segment of the FCD model
由于部分介于0.3~0.6 的实测植被覆盖度对应的预测值小于0.3,利用FNDVI代替FMSAVI在0.0~0.3 内的植被覆盖度进行反演时会使这部分值偏小,使得总体预测结果不理想。对0.0~0.3 内的植被覆盖度继续分段研究发现在植被覆盖度介于0.0~0.1 时复合植被指数NDVI 预测结果更贴近现实,在植被覆盖度介于0.1~0.3 时复合植被指数NDVI 虽反演效果更好,但考虑研究区整体植被覆盖度反演效果,最终选取FNDVI(0.0~0.1) + FMSAVI(0.1~1.0)对植被覆盖度进行反演(表6)。

表6 FCD 模型优选植被指数精度分析Table 6 Accuracy analysis of optimal vegetation indices in the FCD model
2.5 模型精度验证
分别采用分段回归模型、结合分段优势的FCD模型对研究区植被覆盖度进行反演,并基于验证样本进行精度评价及模型比较。结合图3、图4 可知,两种模型PRECISION 均约为79%,但相比于分段回归模型,基于分段优势的FCD 模型建模集R2提高0.024 7,RMSE 降 低0.010,验 证 集R2提 高0.023 9,RMSE 降低0.002,PRECISION 提高1.189%,说明综合分段优势的FCD 模型反演结果更准确,可适合用于研究区植被覆盖度的精准反演。

图3 分段回归模型精度验证图Figure 3 Verification of the accuracy of the segment regression model
进一步采用分段回归模型和综合分段优势的FCD 模型对研究区植被覆盖度进行反演(图5)发现,两种反演方法估算的研究区植被覆盖度在整体上具有较为一致的空间分布趋势,但在不同植被覆盖度等级还存在一定的反演差异,主要体现在低覆盖度与中覆盖度(植被覆盖度为0.3 和0.7)处反演结果差异较大。结合实地调查数据及景观照片,并通过Google Earth 地图和研究区植被覆盖度反演图对比发现,分段回归模型在植被覆盖度为0.3 及0.7 处反演效果较差,植被覆盖度较为集中,其误差较大;而基于分段优势的FCD 模型在低覆盖度与中覆盖度的总体反演结果更贴近现实,再次说明综合分段优势的FCD 模型更适合用于研究区总体植被覆盖度的反演,具有较高的反演精度。
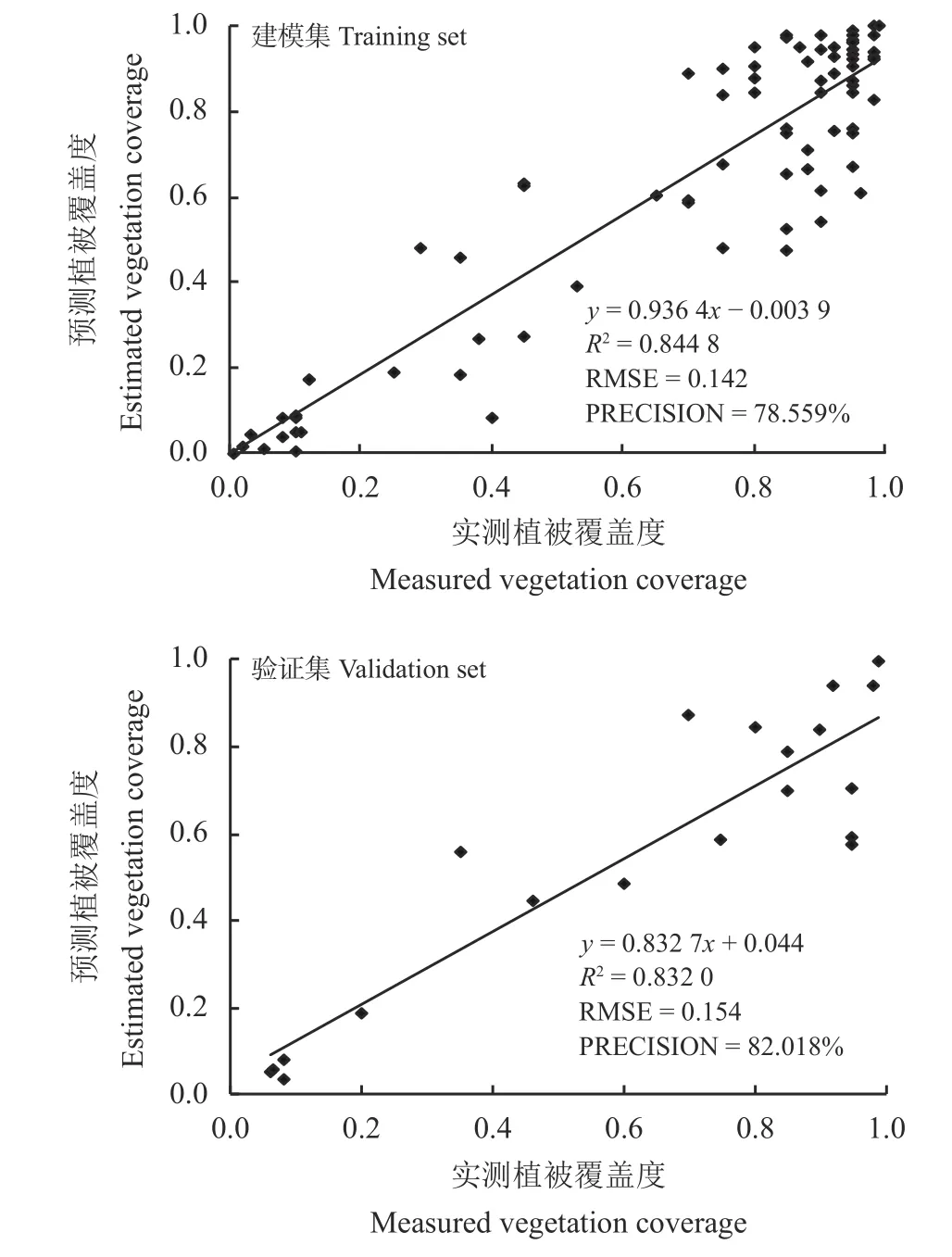
图4 基于分段优势的FCD 模型精度验证图Figure 4 Verification of the accuracy of the FCD model based on segment advantage
3 讨论与结论
本研究表明,分段回归模型在建模时具有较高的精度,但在反演植被覆盖度时由于分段点处存在像元重合现象,经像元平均处理后仍与实测植被覆盖度存在一定误差,整体植被覆盖度反演效果较不理想,这与李鑫川等[29]的研究结果较为一致。因此,对于植被覆盖度较为集中且已有相关实测数据的区域,使用分段回归模型估测植被覆盖度,其结果能够更贴近现实;对于植被组成结构复杂,植被覆盖度变化范围较大的地区,利用综合分段优势的FCD 模型可得到较好的反演效果。
受地形地貌、地表植被等多种因素的影响,不同植被指数具有不同的适用条件。在不同植被覆盖度区间,选择正确的植被指数进行反演,对植被覆盖度的精准估测研究具有重要意义。江洪等[27]发现FCD 模型不仅适用于Landsat TM 影像,也适用于SPOT 影像,植被覆盖度反演总体精度可达80%以上。蔡蘅等[28]发现FCD 模型反演植被覆盖度具有较高精度,并使用其对且末绿洲植被覆盖度时空变化进行分析。但上述研究仅使用一种植被指数对植被覆盖度进行反演,其反演精度有待提高。张成才等[30]通过计算热量指数对FCD 模型进行改进,发现改进后的FCD 模型提高了植被覆盖度反演精度。夏颖等[10]基于FCD 模型选用4 种植被指数,对裸土指数、阴影指数进行改进,构建复合指数代入像元二分模型反演植被覆盖度,发现所得精度普遍高于对应的单独植被指数,其中利用复合植被指数TSAVI 精度最高。但FCD 改进模型应用具有一定地域性,其是否能够大面积推广还有待进一步验证。本研究基于传统FCD 模型使用分段方式,选取各段最优复合植被指数反演植被覆盖度,发现此方法具有较高精度,能够为其他地区植被覆盖度反演提供一定的方法参考。针对特定区域,基于FCD 改进模型采用分段方式选取最优复合植被指数对植被覆盖度进行反演,其反演精度将会进一步提高。
结合野外实测植被覆盖度数据选取9 种植被指数进行相关性分析,通过选择敏感植被指数基于分段方式采用回归模型及FCD 模型对渭干河-库车河三角洲绿洲植被覆盖度进行反演,可以得到以下结论:
1)根据实测数据计算不同植被指数在植被覆盖度变化范围内的比例发现:Fc≤ 0.3 时,不同植被指数分段百分比变化较为一致,0.3 < Fc≤0.7 时,各个植被指数的变化幅度也较为一致,大部分植被指数累积百分比接近70%,0.7 < Fc≤ 1.0 时,这9 种植被指数变化幅度较大,因此以0.3 及0.7 作为反演植被覆盖度的分段点。
2)分段回归模型在选择最优植被指数时考虑不同植被指数存在差异会使反演图出现像元重合或缺失现象,为减少差异、提高反演精度需综合考虑相关性高、分段累计变化量较小及分段累计百分比较高的条件进行选取,此模型中MSAVI (0.0~0.3)、GNDVI(0.3~0.7)、IPVI (0.7~1.0)为反演最佳植被指数。
3)综合分段优势的FCD 模型中复合植被指数NDVI (0~0.3)、MSAVI (0.3~0.7、0.7~1.0)为反演最佳植被指数,由于部分介于0.3~0.6 的实测植被覆盖度对应的预测值小于0.3,继续研究发现0.1 可为FCD 模型反演植被覆盖度的一个分段点,考虑研究区整体植被覆盖度反演效果,最终选取FNDVI(0.0~0.1) + FMSAVI(0.1~1.0)对植被覆盖度进行反演。
4)分段回归模型及基于分段优势的FCD 模型建模集PRECISION 均约为79%,但相比于分段回归模型,基于分段优势的FCD 模型建模集R2提高0.025,RMSE 降低0.010,其验证集R2提高0.024,RMSE 降低0.002,PRECISION 提高1.189%,更适合用于研究区整体植被覆盖度反演,并可为其他地区植被覆盖度反演提供一定方法参考。
由于受研究区地表环境条件的限制,本研究在后续工作中,还需使用更加科学的植被覆盖度调查方法,增加对低植被覆盖度区域地表植被的调查,寻求像元替换的最佳方法,对研究结果再做进一步的优化。
