可配置八阶巴特沃斯低通滤波器的设计
2021-04-20朱思浩罗显志
朱思浩,罗显志
(湖北大学计算机与信息工程学院, 湖北 武汉 430062)
0 引言
滤波器常用的近似函数有4种:巴特沃斯函数、切比雪夫函数、椭圆函数、贝塞尔函数.用巴特沃斯函数设计低通滤波器,仿真出来的幅频特性曲线平坦,通常无起伏情况,阻频带持续降低,直至变为零.在设计高阶巴特沃斯低通滤波器时,前人通常用级联设计法串联数个二阶巴特沃斯低通滤波器的设计思路,形成高阶巴特沃斯低通滤波器电路,再仿真其幅频特性曲线.本设计在原有基础上,做了两点修改.首先,对电路结构进行修改.ADA4084-2是一种轨至轨输入和输出的双通道,单电源,10 MHz带宽的芯片,用ADA4084-2做为电路的运算放大器,它具有带宽大、噪声低、精度高的优点.每一级运算放大器的反向输入端接到下一级电路的电容[1].其次对设计的八阶巴特沃斯低通滤波器进行噪声分析.因为频谱噪声密度是反映滤波器噪声干扰强弱的重要指标,通过与AD8671芯片的频谱噪声密度曲线进行比较,看出设计的八阶巴特沃斯低通滤波器在截止频率处的抗噪声干扰能力的强弱.
1 巴特沃斯滤波器的传递函数
其系统函数归一化形式为:
通常情况下保持通带增益为0 db,设定d0=a0,在a0=an=1时,可以得到归一化巴特沃斯多项式因子:当滤波器的阶数N=1时,它的多项式因子为s+1;滤波器的阶数N=2时,多项式因子为s2+1.414s+1;滤波器的阶数N=3时,多项式因子为(s+1)(s2+s+1);滤波器的阶数N=4时,它的多项式因子为(s2+0.765 4s+1)(s2+1.847 8s+1);一直到滤波器的阶数N=8时,多项式因子为(s2+0.398 6s+1)(s2+1.111s+1)(s2+1.663 0s+1)(s2+1.962 2s+1).为了便于理解,可用如表1来表示从一阶滤波器至八阶中,全部的多项式因子.

表1 归一化的巴特沃斯多项式
由a0=an=d0=1时,可以得到如下公式:
此时的Butterworth多项式为:
sn+an-1sn-1+…+a2s2+a1s+1(a0=an=1)
用振幅的平方对频率的关系来表示巴特沃斯低通滤波器,如下式所示:
上式中,n表示滤波器的阶数,wc是截止频率,ωp是通频带边缘频率,1/(1+ε2)=|H(ω)|2是通频带边缘数值.如果该滤波器是N阶的情况下,其相应的振幅和频率之间有这样的一种关系:
式中,G是放大率,H是转移函数,j是虚数单位,n是级数,w是角频率.假设截止频率wc=1的情况下,那么,该公式归一化就是:
2 电路结构
八阶巴特沃斯低通滤波器的设计方法有多种,本设计在原有基础上,对电路结构进行修改.八阶巴特沃斯低通滤波器电路选用ADA4084-2型运算放大器芯片,该芯片具有带宽高、低噪声、精度高、单位增益高的优点,适合高阶低通滤波器的设计.该电路是由4个改进后的二阶Sallen-Key低通滤波器串联形成.改进后的二阶Sallen-Key低通滤波器电路结构如图1所示.

图1 改进后二阶Sallen-Key低通滤波器结构图
由图1可以看出二阶Sallen-Key低通滤波器电路结构中,以ADA4084-2芯片作为Sallen-Key低通滤波器的有源器件,1个交流电压源,2个电阻和1个电容相互连接接到ADA4084-2的同相输入端,ADA4084-2的反相输入端与1个电容的一端直接接到下一级放大电路中[2-3].根据基尔霍夫电压规律,基尔霍夫电流规律和运算放大器同相端的关系可以得到电路的传递函数.传递函数如下所示:
(1)
3 电路参数计算
设计此滤波器所用到的公式如下:
(2)
(3)
式中,W0为低通滤波器的转折频率,Q为低通滤波器的品质因数,R1、R2、C1、C2分别表示八阶低通滤波器第一级电路中电阻和电容.根据图1可知,1个二阶Sallen-Key滤波器中有4个未知数,它们分别是R1、R2、C1、C2. 由(2)式和(3)式来确定R1、R2、C1、C2.由于方程的个数少于未知数的个数,不能直接通过方程来依次求解出R1、R2、C1、C2的数值.因而在求解这4个未知数时,必须要先确定2个电路元器件的参数值,然后再根据不同电阻电容之间的关系来确定剩下2个值,从而求解出R1、R2、C1、C2的数值[4-7].
在对低通滤波器中电阻电容等相关参数进行取值时,经常用到等值元件法.在该电路若用等值元件法对各级电路中的电阻电容进行取值,即C1=C2,R1=R2;电路中只有2个未知的参数值:C1,R1,再根据滤波器电路的截止频率与电容选取的关系确定电容C1,再将C1带入上述(2)式,可以求得电阻R1.作为设计电路的一种方法,使用等值元件法设计电路其目的是为了减小元件的分散性,计算参数值时相对简便;但是使用等值元件法缺点很明显.首先电路的截止频率不能设置的太高,其次是对电路中Q值有所限制.考虑到使用等值元件法设计滤波器电路的诸多限制,所以用另外一种设计方式来设计该滤波器.[8]设计该滤波器,第一步要选择合适的电容的阻值.通过分析可以清楚的了解到,在此需要进行设计的电路中,需要用到200 kHz的截止频率,同时,还要充分分析其截止频率、电容的情况,并且要按照它们选取的关系确定各级电路中电容值[9-10].为了便于叙述,通过表2展现八阶巴特沃斯低通滤波器各级电路的电阻、电容值.

表2 各级电路电阻电容数值表
八阶巴特沃斯低通滤波器电路图如图2所示:

图2 八阶巴特沃斯低通滤波器
4 仿真结果
通过对此滤波器进行分析,并且通过NI Multisim 14.0对其电路图进行仿真,得到以ADA4084-2型运算放大器,为八阶巴特沃斯低通滤波器的有源器件的幅度特性曲线图,如图3所示.

图3 幅度特性曲线图
以ADA4084-2型运算放大器,为八阶巴特沃斯低通滤波器的有源器件的频谱噪声密度曲线图如图4所示.
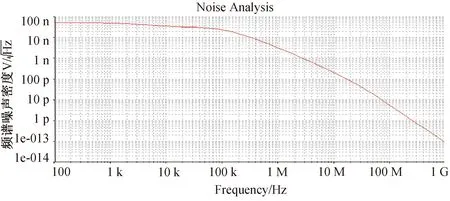
图4 频谱噪声曲线图
以AD8671运算放大器芯片做为八阶巴特沃斯低通滤波器有源器件,用NI Multisim 14.0绘图工具进行仿真得到幅度特性曲线图,如图5所示.
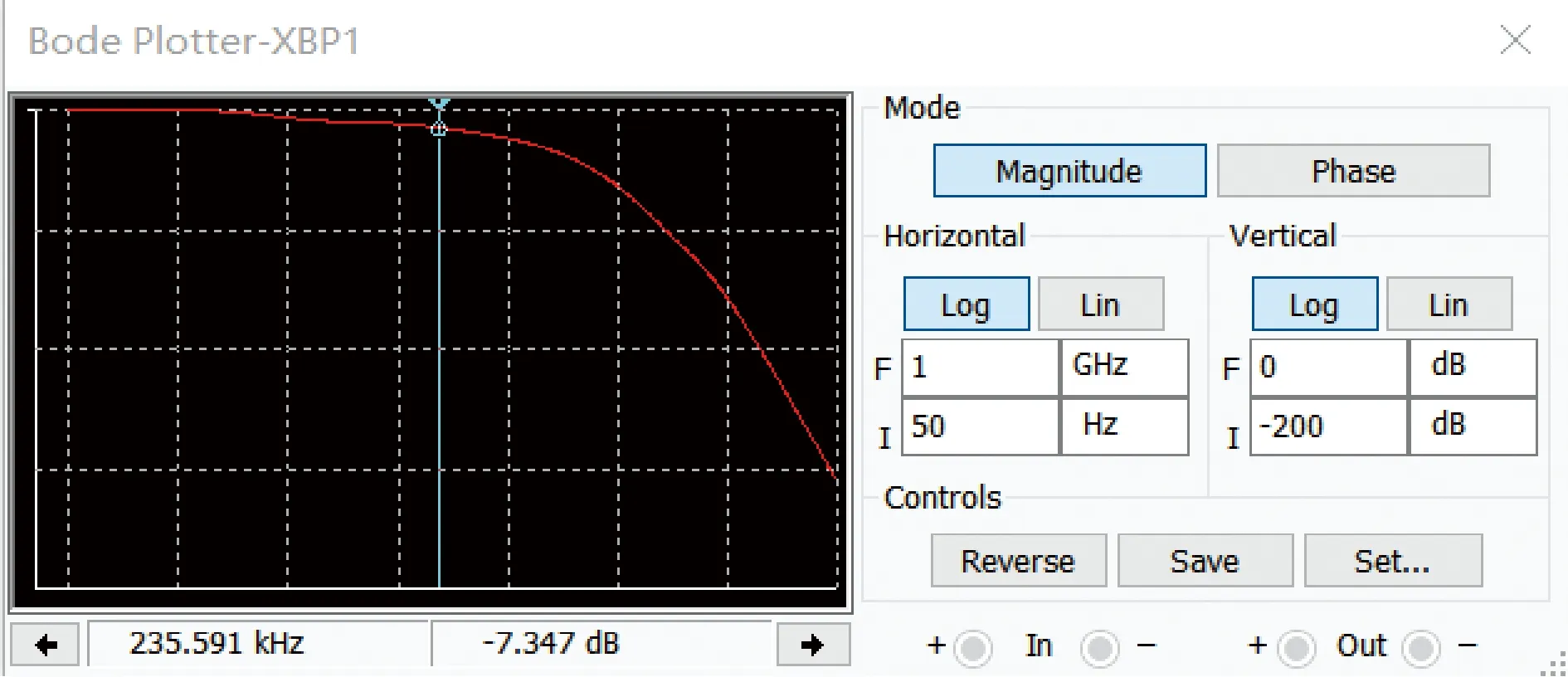
图5 幅度特性曲线图
以AD8671运算放大器芯片作为八阶巴特沃斯低通滤波器有源器件,其所对应的频谱噪声密度曲线如图6所示.

图6 频谱噪声曲线图

5 结论
通过将ADA4084-2型运算放大器与AD8671运算放大器芯片的噪声分析比较可知:当噪声频率在电路截止频率200 kHz处,ADA4084-2型运算放大器噪声频谱密度值低于AD8671运算放大器噪声频谱密度值,噪声频率高于200 kHz时,ADA4084-2型运算放大器的噪声的频谱密度曲线,比AD8671运算放大器频谱密度曲线下降的快.综上可知:以ADA4084-2型运算放大器作为八阶巴特沃斯低通滤波器的有源器件是合适的,设计的八阶巴特沃斯低通滤波器抗信号的噪声干扰性能强,在滤波器领域有较大的应用前景.
