压水堆堆芯多专业耦合计算软件COMPCS的研制与初步应用

李治刚，安 萍，潘俊杰，赵文博，刘卢果，宫兆虎，芦 韡,强胜龙，贺 涛

(中国核动力研究设计院 核反应堆系统设计技术重点实验室，成都610213)

由于轻水堆的中子物理与热工水力之间存在强烈的反馈现象，故在进行压水堆的堆型设计与安全分析时必须考虑物理-热工耦合现象[1]。为能准确模拟反应堆物理-热工耦合现象，近年来，国内外针对轻水堆开展了大量的物理-热工耦合研究，研发了反应堆多物理耦合计算方法和模拟软件。例如，针对堆芯的物理-热工耦合计算程序有PARCS[2]，DYN3D[3]，ANCK[4]，NODAL3[5]，NALSANMT/CORBA-IV[6]等；包含反应堆系统及堆芯物理-热工耦合的计算程序有PARCS/TRACE[7]，CTSS[8]，DYN3D/ATHLET[3]等。在对存在明显物理-热工反馈且堆芯功率分布不均的事故过程分析中，必须采用3维物理-热工耦合分析方法。弹棒事故是反应性事故中最严重的一种[9]，可能会威胁燃料棒包壳和压力容器的完整性，在压水堆安全分析中必须对其进行评价。传统的弹棒事故评价方法是采用2维与1维相结合的方法模拟堆芯中子动力学。近年来，美国和法国发展了3维动力学分析方法用于弹棒事故分析，如法国AREVA公司开发的SMART 3D+FLICA III+THEMIS+COMBAT系统[10]、美国西屋公司开发的TWINKLE+FACTRAN+LOFTRAN系统[11]及美国核管理委员会开发的PARCS/TRACE/ROBIN系统[12]，已分别用于岭澳核电站、大亚湾核电站和秦山核电站二期的弹棒事故分析。我国也开发了多套3维时空中子动力学计算软件，如中国核动力研究设计院开发的CORCA-K[13]及西安交通大学开发的NECP-Bamboo[14]等，这些软件为研发自主的弹棒事故3维动力学分析系统提供了基础。

本文基于堆芯3维时空中子动力学计算软件CORCA-K、堆芯热工水力计算软件CORTH[15]及截面更新计算软件PACFAC，针对典型压水堆的物理-热工3维瞬态耦合计算问题，自主研发了堆芯多专业耦合计算软件COMPCS，采用压水堆弹棒基准题NEACRP[16]和MOX/UO2[17]，对COMPCS软件进行了验证，并对“华龙一号”堆芯首循环寿期初和寿期末的弹棒事故进行了计算与分析。

1 理论模型

1.1 3维时空中子动力学方程求解方法

3维时空中子动力学多群中子扩散方程可表达为[18]

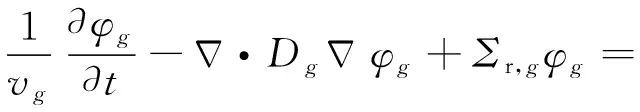
(1)

(2)

其中，g为能群号；i为缓发中子先驱核组号；G为能群数；χp,g和χd,g分别为瞬发中子裂变谱和缓发中子裂变谱；Dg为第g群中子扩散系数；Σf,g′为第g′群裂变宏观截面；φg为第g群中子注量率；υg′为第g′群平均裂变中子数；Σs,g′→g为第g′群到第g群的散射截面；Σr,g为第g群的移除截面；vg为第g群中子速度；βi和β分别为第i组缓发中子份额和缓发中子总份额；Ci为第i组缓发中子先驱核浓度；λi为第i组缓发中子先驱核衰变常数。

目前，求解式(1)的典型方法主要为有限差分法、节块法和有限元方法。其中，节块法具有较高的计算效率和精度，在商业软件中应用广泛。节块法的特点是对式(1)进行横向积分，将3维问题的求解变成联立求解3个1维方程。在网格m内，对给定的坐标方向x，对式(1)沿与x方向垂直的另2个方向(y,z)进行积分，可得到1维方程为

Qg,x(x)-Lg,x(x)，g=1,…，G

(3)

其中，φg,x，Qg,x，Lg,x分别为x方向横向积分中子注量率、源项(包括裂变源项和散射源项)和横向泄露项。同理可得y和z方向相应的1维方程。

CORCA-K 求解式(3)时，采用第二类边界格林函数节块法进行空间离散，采用二阶对角线隐式龙格库塔格式(diagonal implicit Runge Kutta，DIRK)进行时间离散[19]，详细的处理过程可参见文献[13]。

1.2 热工水力计算方法

COMPCS软件中除采用闭式单通道计算模型和圆柱瞬态导热模型计算冷却剂温度和燃料温度外，还建立了与堆芯热工水力计算软件CORTH对应的接口，从而实现对堆芯热工参数子通道的模拟。CORTH软件基于具有滑速比的四方程模型，适用于反应堆堆芯或棒束实验热工水力分析。本文主要介绍典型单通道模型的计算方法，子通道模型可参见文献[15]。

1.2.1闭式单通道计算模型

冷却剂单相单通道的瞬态守恒方程为

(4)

(5)

其中，ρ为冷却剂密度， kg·m-3；h为冷却剂质量焓， J·kg-1；u为冷却剂流动速度， m·s-1；q为体积热流密度， W·m-3；t为时间， s。

1.2.2圆柱瞬态导热模型

圆柱瞬态导热模型的守恒方程为[20]

(6)

其中，cp为材料的质量定压热容， J·(kg·K)-1；ρf为材料密度， kg·m-3；λ为热导率， W·(m·K)-1；T为热力学温度， K。

在径向上，将燃料芯体划分为n个网格，气隙为1个网格，将包壳划分为2个网格。在空间上，采用有限体积法或有限差分法对式(6)进行离散。在时间上，采用全隐式格式。采用高斯-赛德尔迭代计算得到燃料元件的径向温度分布，采用罗兰公式计算燃料有效温度[21]。

1.3 物理-热工耦合算法

COMPCS软件的耦合计算流程，如图1所示。采用CORCA-K控制时间迭代流程，基于CORCA-3D软件提供的稳态燃耗状态库[22]，在每个迭代步内调用CORTH或闭式单通道模型更新热工水力参数，如冷却剂温度和密度，调用圆柱瞬态导热模型计算燃料有效温度，PACFAC软件可基于新的状态参数更新材料截面。在稳态时，采用Picard迭代策略[23]，保证每个迭代步内中子物理和热工水力均收敛后才进入下一个迭代步。

2 数值验证

本文采用压水堆弹棒基准题NEACRP和MOX/UO2对COMPCS软件的物理-热工耦合计算精度进行验证。

图1 COMPCS软件的耦合计算流程Fig.1 Flow chart of coupling calculation process of COMPCS

2.1 NEACRP基准题

NEACRP基准题是1991年由Finnemann等建立的，主要用于轻水堆堆芯3维物理-热工耦合软件的验证。该基准题参考了典型压水堆的几何尺寸和运行状态，堆芯布置157个燃料组件和1圈径向反射层，轴向分为18层。根据初始功率水平和控制棒弹出位置的不同，可将堆芯分为A1，A2，B1，B2，C1，C26种工况。其中，A1，B1，C1为热态零功率(hot zero power, HZP)，A2, B2, C2为热态满功率(hot full power，HFP)，堆芯功率为2 775 MW，共有6组缓发中子，总缓发中子份额为0.007 6。NEACRP基准题的几何尺寸划分、材料截面及控制棒移动信息可参见文献[16]。

本文利用COMPCS软件计算了6个工况的主要参数，并与NEACRP基准题的参考结果进行比对。该参考结果是1997年发布的修订版数据，由PANTHER程序采用精细时空网格计算得到。

表1列出了稳态及瞬态主要参数的对比情况。由表1可见，临界硼质量分数与参考结果的偏差在5×10-6以内，相对偏差均小于0.5%；堆芯相对功率峰值的最大偏差出现在B1和C1工况中，相对偏差分别为2.37%和2.35%，其余工况的相对偏差在1%以内；瞬态结束时堆芯相对功率最大偏差出现在零功率工况中， A1，B1，C1的相对偏差分别为1.57%，1.35%，1.37%；瞬态结束时燃料多普勒温度与参考结果的相对偏差均在1%以内。

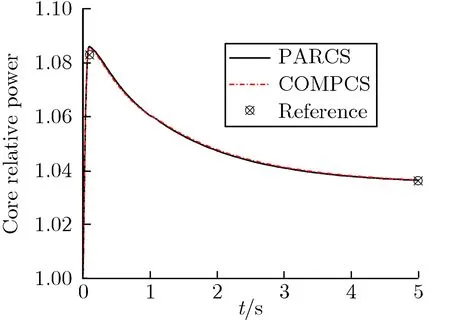
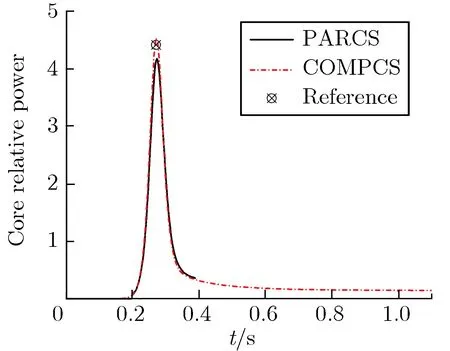
图2 为NEACRP基准题相对功率随时间变化情况的对比。为进行比较，图2还给出了PARCS软件的计算结果。由图2可见，在满功率工况中，COMPCS软件计算结果与PARCS结果基本一致，堆芯相对功率峰值与参考结果的相对偏差均在1%以内；在零功率工况中，COMPCS软件计算结果与PARCS结果趋势一致，堆芯相对功率峰值更接近参考结果。

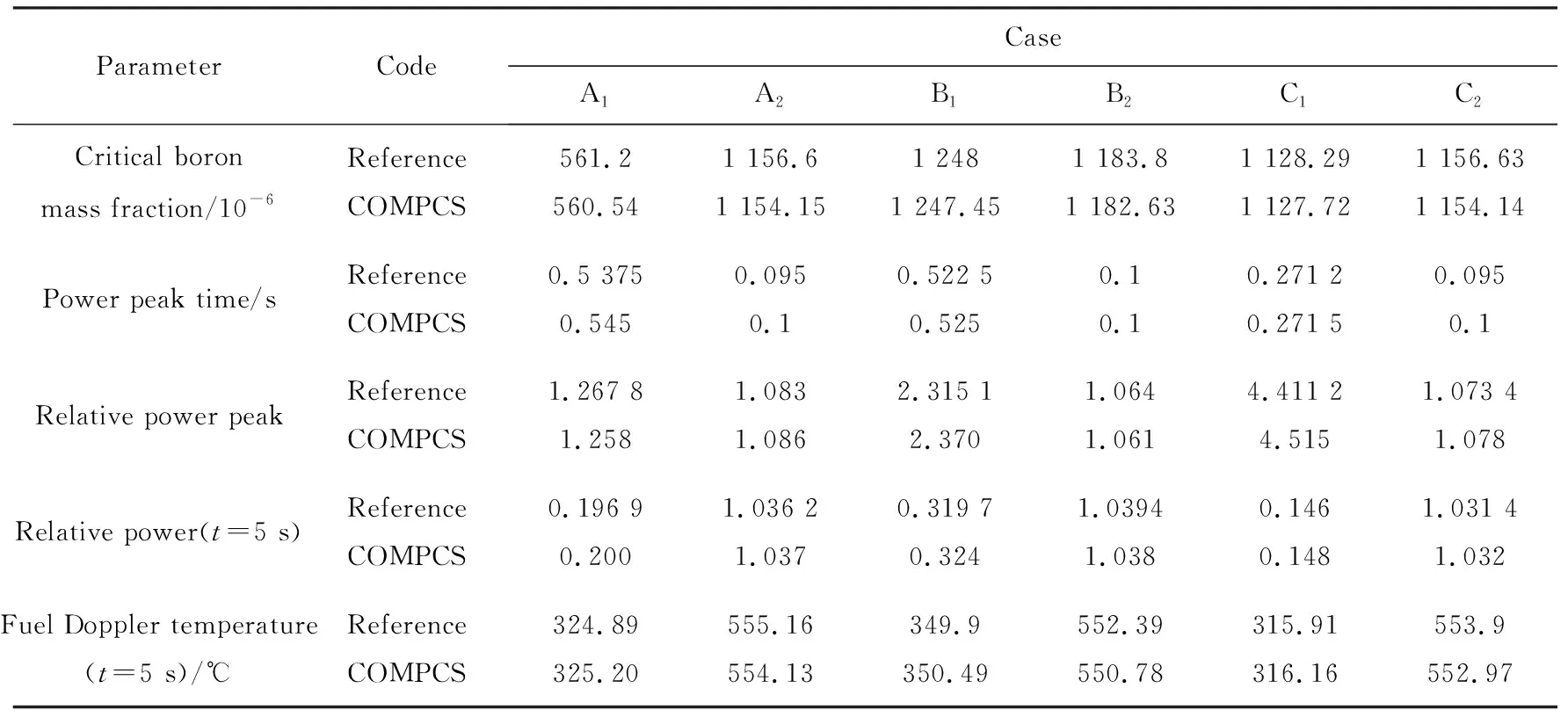
表1 NEACRP基准题稳态和瞬态主要参数与参考结果的对比Tab.1Comparison of steady and transient main parameters with reference results in NEACRP benchmark

(a)A1

(b)A2

(c)B1

(d)B2

(e)C1

(f)C2图2NEACRP基准题相对功率随时间变化情况的对比Fig.2 NEACRP benchmark relative power vs. time

2.2 MOX/UO2基准题

由于武器级MOX燃料的中子动力学参数与典型压水堆有显著差别，2006年由OECD/NEA组织建立了压水堆弹棒MOX/UO2基准题。该基准题基于西屋四环路全尺寸的压水堆核电站模型，堆芯额定功率为3 565 MW，共有193个燃料组件(UO2燃料组件141个，MOX燃料组件52个)，可模拟平衡循环中一组控制棒的弹出过程。MOX/UO2基准题包含4个部分：第1部分为2维固定物理-热工工况，给出了特征值、棒价值、组件和栅元精细功率；第2部分为3维满功率工况，给出了临界硼质量分数、组件和栅元功率；第3部分为3维零功率工况，给出了临界硼质量分数、组件和栅元功率；第4部分为基于第3部分的瞬态工况，给出了控制棒弹棒瞬态响应参数，包括堆芯功率和反应性等。采用组件程序建模可得到MOX/UO2基准题组件的少群参数。 MOX/UO2基准题堆芯、组件几何尺寸及控制棒移动信息可参见文献[17]。

图3为MOX/UO2基准题瞬态工况相对功率随时间变化情况的对比。选取PARCS 2G软件的计算结果作为比对参考结果，表2列出了MOX/UO2基准题稳态工况计算结果的对比情况。由于第1部分为固定截面计算，不涉及物理-热工耦合迭代，所以本文未对第1部分进行模拟计算。

由图3可见， COMPCS计算的相对功率峰值为1.644，该值与PARCS 2G软件、PARCS 8G 软件及CORETRAN软件计算结果的相对偏差分别为14.49%，-4.6%，1.2%。由表2可见，COMPCS软件计算的稳态关键参数中，第3部分的Fxy与参考结果的相对偏差为1.04%，其他参数的相对偏差均在1%以内。

验证结果表明，COMPCS软件对NEACRP基准题和MOX/UO2基准题的计算精度与国际同类软件相当，计算精度较高。

图3 MOX/UO2基准题瞬态工况堆芯相对功率随时间的变化Fig.3 Relative power vs. time in MOX/UO2benchmark transient condition

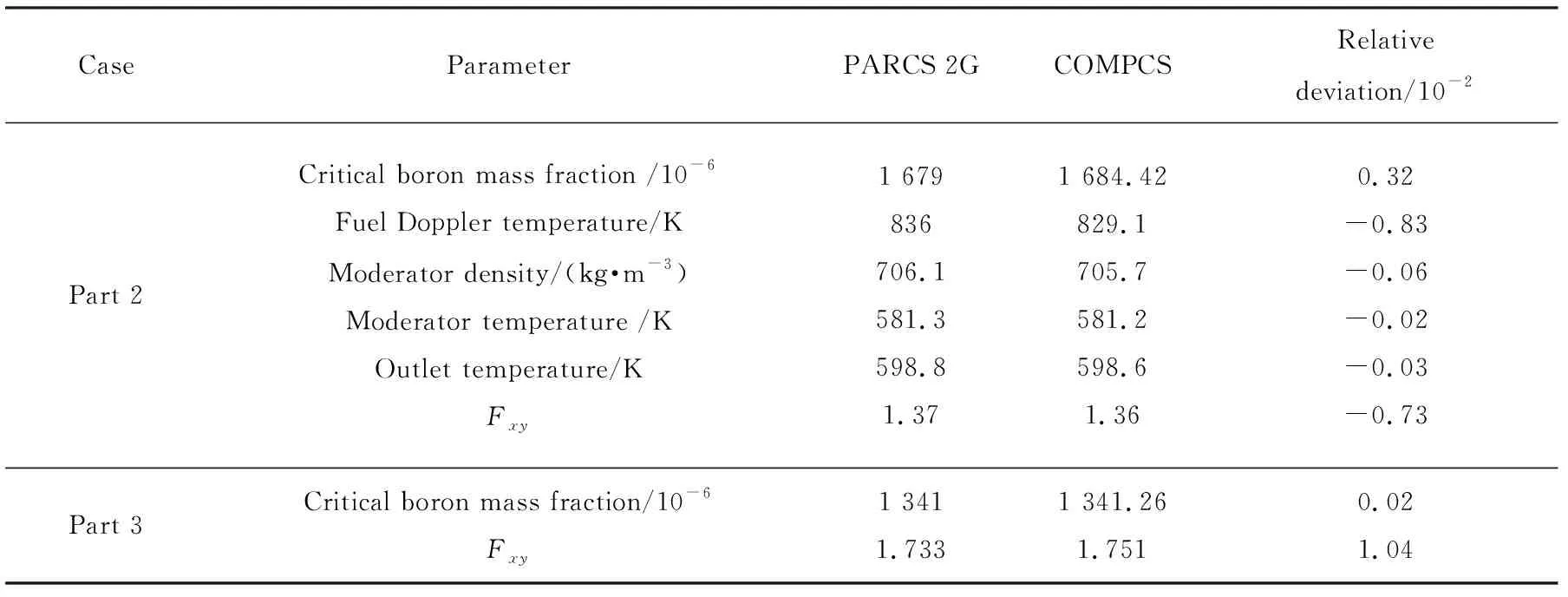
表2 MOX/UO2基准题稳态工况的计算结果对比Tab.2Comparison of results of MOX/UO2 benchmark in steady condition calculated by COMPCS and PARCS 2G

3 “华龙一号”堆芯弹棒事故模拟

“华龙一号”(HPR1000)反应堆是我国具有自主知识产权的第三代核电压水堆[24-25]，堆芯由177个AFA3G燃料组件构成，每个组件包含呈17×17方形排列的264根燃料棒、24根导向管和1根测量管。堆芯控制棒组件按功能可分为控制棒组和停堆棒组，控制棒布置可参见文献[24]。控制棒组由功率补偿棒(G1，G2，N1，N2)和温度调节棒(R)构成。停堆棒组(SA，SB，SC)的功能是提供反应堆停堆所必需的负反应性。控制棒组的提出价值由大到小依次为G1，G2，N1，N2，R，但在实际运行中，功率补偿棒采用叠步方式插入或提出，R棒只能在插入限之内运行，G1棒全部插入堆芯的概率最高。因此，本文将模拟G1棒处于全插、其他控制棒处于全提时，G1棒在首循环寿期初(beginning of life, BOL)和寿期末(end of life, EOL)从堆芯弹出后堆芯相对功率及温度等参数随时间的变化情况。计算中设置4个功率水平，分别为25%FP，50%FP，75%FP，100%FP，“华龙一号”首循环燃耗由CORCA-3D软件计算得到[22]。

图4为G1棒在0.1 s内从全插位弹出堆芯后，堆芯相对功率随时间的变化情况。由图4可见，在相同功率水平下，堆芯瞬态功率水平在寿期末和寿期初随时间的变化趋势是一致的，在寿期末4个初始功率水平下的堆芯瞬态功率峰值均高于寿期初，在初始功率水平为50%FP时，寿期末堆芯瞬态功率峰值达到寿期初的1.85倍。

图5和图6分别给出了G1棒在0.1 s内从全插位弹出堆芯后，堆芯燃料芯块温度峰值和包壳温度峰值随时间的变化情况。

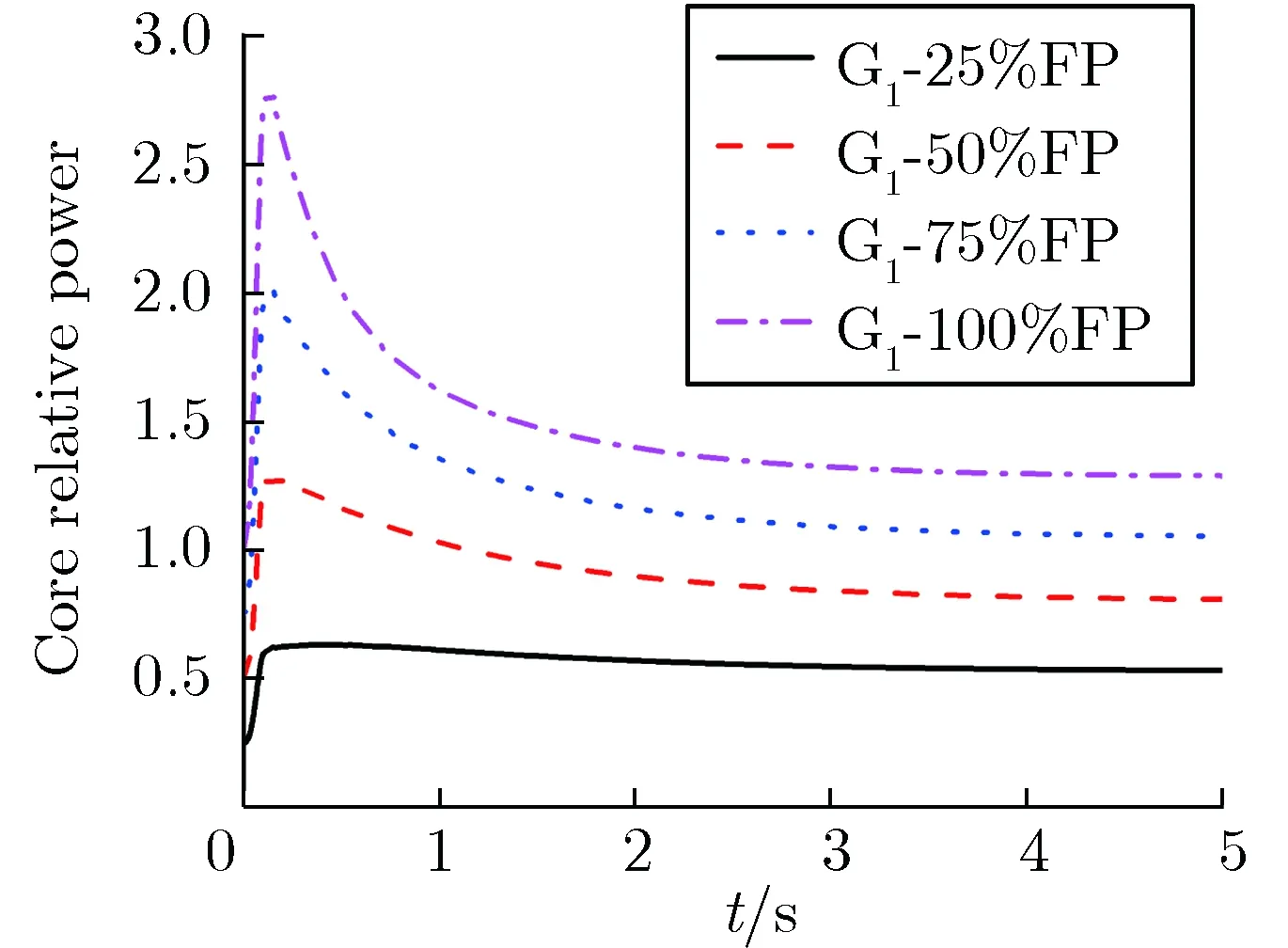
(a)BOL

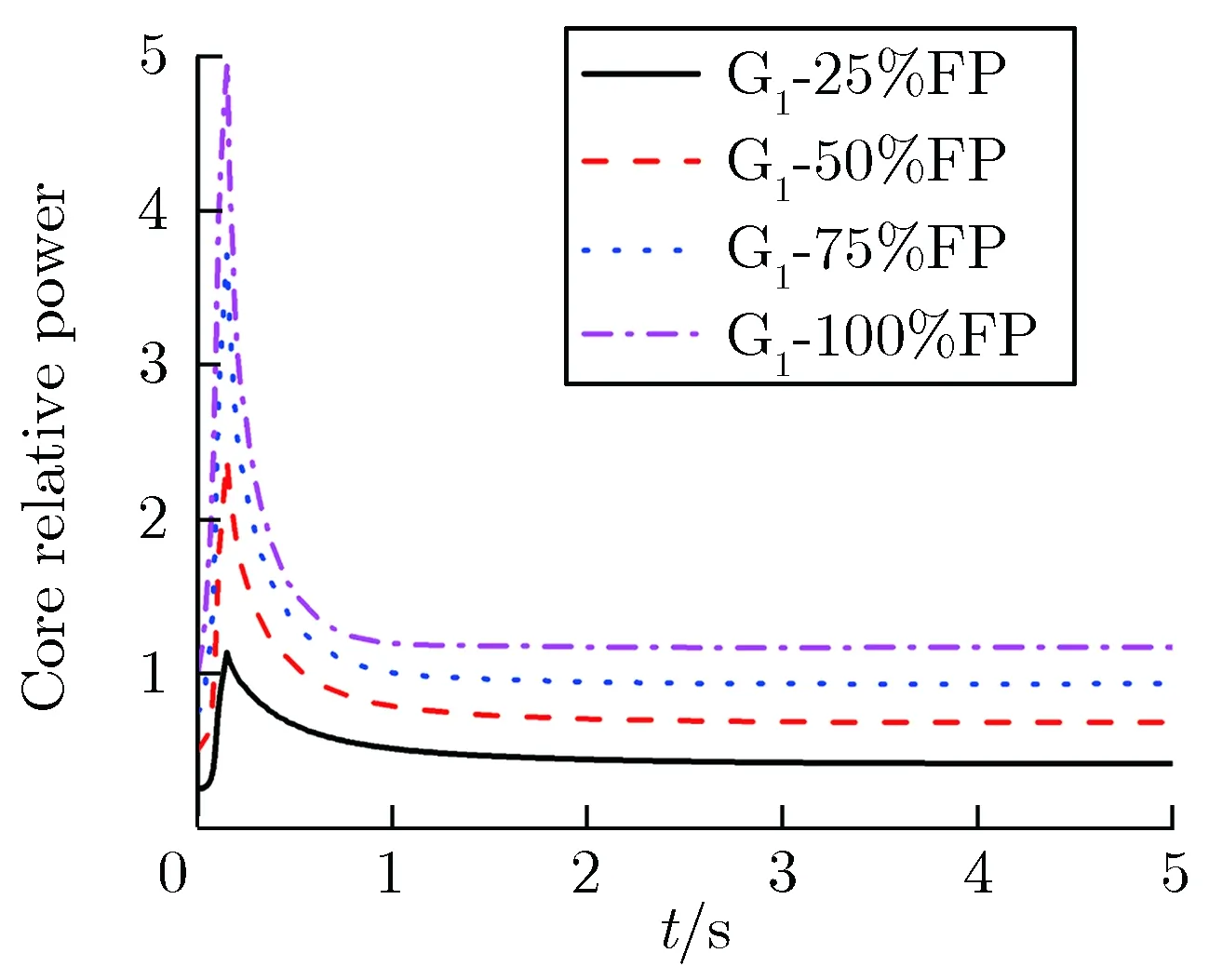
(b)EOL图4堆芯相对功率随时间的变化Fig.4 Core relative power vs. time

(a)BOL

(b)EOL图5燃料芯块温度峰值随时间的变化Fig.5 Fuel core peak temperature vs. time

(a)BOL

(b)EOL图6包壳温度峰值随时间的变化Fig.6 Cladding peak temperature vs. time

由图5和图6可见，在寿期初，随着时间的推进，燃料芯块温度峰值和包壳温度峰值均呈现先增加后稳定在一定水平上的变化趋势；随着功率水平的增加，包壳温度峰值升高的速率也增加。在寿期末，功率水平在50%FP以下时，燃料芯块及包壳温度峰值的变化趋势与寿期初相似，而当功率水平在50%FP以上时，燃料芯块及包壳温度峰值呈现先快速增加、到达峰值后又逐渐减小、最后稳定在一定水平上的变化趋势。

在压水堆中，随着燃耗的加深，UO2燃料芯块会发生肿胀，并释放裂变气体，导致燃料热导率随着燃耗的加深呈下降趋势。此外，随着堆芯中铀的消耗和钚的积累，堆芯中子动力学也会发生明显变化。在相同功率水平下，寿期末由于缓发中子份额的下降，使堆芯即使在与寿期初相同的反应性下，中子增长速度也相对增加，这是图4(b)中功率峰增长速度快于寿期初的主要原因。

为分析弹棒时间对弹棒过程的影响，针对堆芯功率有显著变化的寿期末满功率工况，设置弹棒时间te分别为0.1， 1.0， 3.0 s，计算了堆芯相对功率、燃料芯块温度峰值和包壳温度峰值随时间的变化情况，结果分别如图7和图8所示。

图7 G1棒不同弹棒时间下寿期末满功率工况堆芯相对功率随时间的变化Fig.7 Core relative power vs. time after G1 ejected withdifferent ejection time at EOL HFP condition

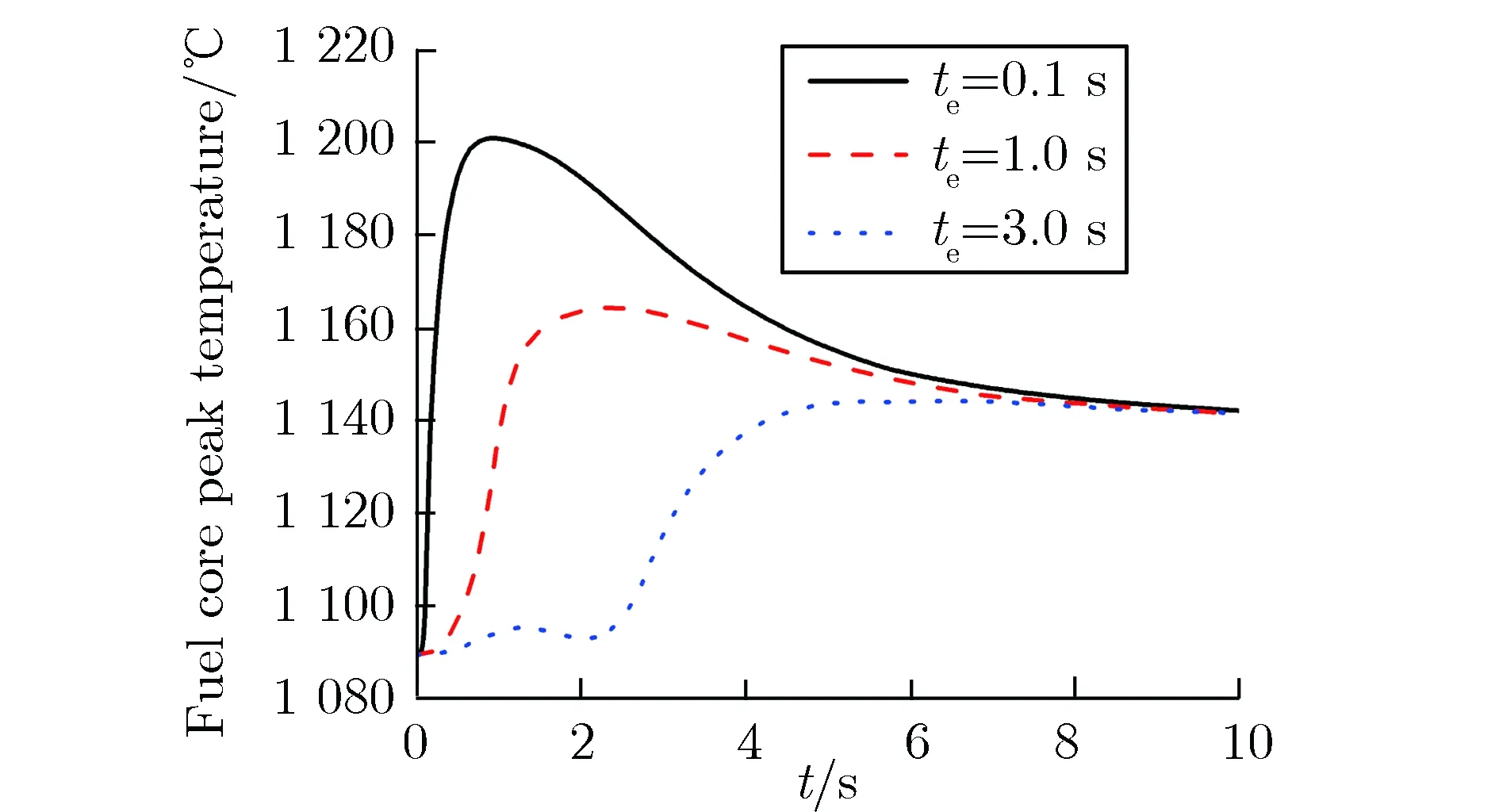
(a)Fuel core peak temperature

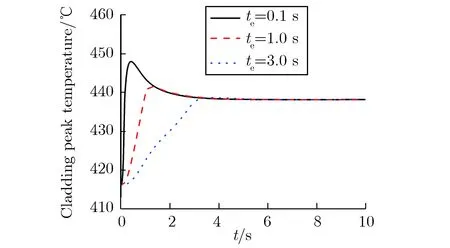
(b)Cladding peak temperature图8G1棒不同弹棒时间下寿期末满功率工况燃料温度峰值随时间的变化Fig.8 Fuel temperature peak vs. time after G1 ejectedwith different ejection time at EOL HFP condition

由图7和图8可见，弹棒时间从0.1 s增加到3 s时，堆芯相对功率峰值从4.958减小到1.36，最终稳定在1.172，燃料芯块温度峰值和包壳温度峰值增加的速率呈现下降趋势。这是因为弹棒引入的反应性是相同的，堆芯相对功率峰值、芯块温度峰值和包壳温度峰值最终均趋于各自的稳定值。

由于COMPCS软件未与系统程序耦合，无法提供一回路压力峰值，所以本文只选择堆芯参数对弹棒过程进行评价。计算结果表明，堆芯燃料芯块温度峰值远低于芯块熔化温度，包壳温度峰值低于包壳熔化温度，因此，在不同功率水平和不同弹棒时间下，G1棒弹棒事故不会威胁燃料包壳的完整性。

4 结论

本文研制的COMPCS软件在模拟压水堆堆芯物理-热工耦合稳态工况及瞬态弹棒过程时，计算结果与NEACRP和MOX/UO2基准题的参考结果符合良好，具有较高的精度；不同初始功率水平、燃耗状态和弹棒时间对“华龙一号”弹棒过程有明显影响，在寿期末、初始功率水平较高及弹棒时间较短时，堆芯相对功率上升的速率更快，会形成功率峰值及燃料温度峰值；“华龙一号”首循环G1棒弹出的典型工况下，燃料芯块温度峰值和包壳温度峰值均低于设计限值，不会威胁燃料包壳的完整性。